水泥余热电厂空冷岛振动空沟减隔振效果数值分析
2021-12-23田松峰丁闪闪李昊晨
田松峰,丁闪闪,李昊晨
(华北电力大学 能源动力与机械工程学院,河北 保定 071003)
0 引 言
国民经济建设的快速发展拓宽了大型动力设备的使用场合,而动力机器基础的振动问题亦是一个广泛存在的问题[1]。这些机器设备基础的强烈振动有时不仅对其自身的正常生产造成威胁,还可能通过振动波的传播影响周围的建筑结构及设备[2]。山西西山华通水泥余热发电机组在建成试运行阶段,发现空冷岛在运行时振动值偏大,检查发现厂内生料磨停运时空冷岛风机振动值正常,在生料磨正常运行时空冷岛风机振动值达12.6 mm/s。《空冷系统运行说明书》中指示:当DCS检测到风机的振动速度大于6.3 mm/s时保护性停机,故空冷岛风机在生料磨运行时无法正常投运。
鉴于生料磨和空冷岛等已建设备结构的工艺控制与设计要求,改变此两者的结构与布置需考虑的情况较为复杂[3,4],本文拟考虑从振动波传播途径上对振动问题进行控制[5]。隔振空沟因效果显著、施工方便的特点在实际中应用广泛[6]。孙立强[7]等通过试验对比,研究了空沟、碎石填充沟以及排桩的隔振效果。叶茂[8]等模拟了沟屏障对某古遗址的隔振作用,认为沟深及位置的改变会显著影响古建筑相关部位的振动响应。基于以上分析,拟利用ABAQUS建立生料磨基础土体?空冷结构的三维计算模型,重点分析将隔振空沟应用于生料立磨运行诱发的低频振动治理上的效果,通过改变空沟深度、宽度和距振源距离等参数,对比空沟后土体以及空冷岛上部风筒梁的振动情况。通过数值分析结果所反映的规律,找到针对本工程问题最经济有效的隔振方案。
1 有限元模型
1.1 模型尺寸
土体模型长80 m,宽40 m,深度方向据场地实际土体分层情况取为40 m,长18 m,宽12 m,深2 m的长方体基础埋置于地基中。空冷风机单元按1×2方式布置,空冷平台为钢筋混凝土结构,高17 m,其中2 m埋于地下,单台空冷跨度长24.54 m,宽11.88 m,梁柱截面尺寸根据实际情况,柱采用1.5 m×1 m,顶层梁1.3 m×0.6 m,底部梁1m×0.6 m,边梁0.7 m×0.4 m,步道梁0.35 m×0.25 m,风筒梁0.4 m×0.25 m。空冷岛距生料磨距离为20 m。
1.2 接触定义
空冷岛立柱作为与土体直接接触并实现动响应传播的部分,接触的设置至关重要。本文将水泥立柱下部2 m的侧表面和柱底面以及位于柱侧和柱底直接接触的土体表面使用面面接触进行定义。将切向接触选为罚函数,摩擦系数0.5,法向接触选为硬接触[9]。
1.3 材料及参数选取
计算模型中立磨基础、下部土体以及空冷土建结构均采用弹性模型,各部分材料参数见表1。采用瑞利阻尼对土体和混凝土结构施加阻尼,阻尼比取为0.03。
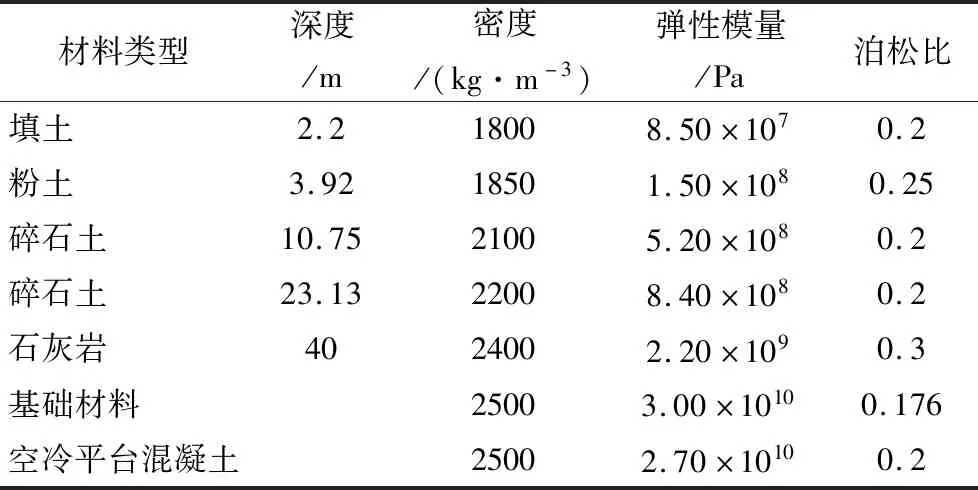
表1 土层分布及材料参数
1.4 生料磨激励荷载条件
生料磨处由于入磨物料的粒度不均,磨机运转时将产生一个不平衡的脉动惯性力,相当于一个随机荷载,文章将立磨基础处实测到的振动加速度时程记录截取5s时长,转换为作用在基础上的荷载激励输入计算模型,进行对生料磨隔振的数值计算。
1.5 边界条件
为防止因设置固定边界而产生波的反射与散射造成计算结果的误差,采用有限元与无限元耦合的方法来处理边界,即将模型四个侧面边界10 m范围和底面边界10 m范围设置成CIN3D8无限元单元[10],其他部分使用C3D8R单元。设置符合精度的单元尺寸后三维有限元模型如图2。输入实测激励后,无减振措施时空冷岛上部风筒梁的振动速度最大值达到12.64 mm/s,与实测值十分相近,验证了模型的正确性。
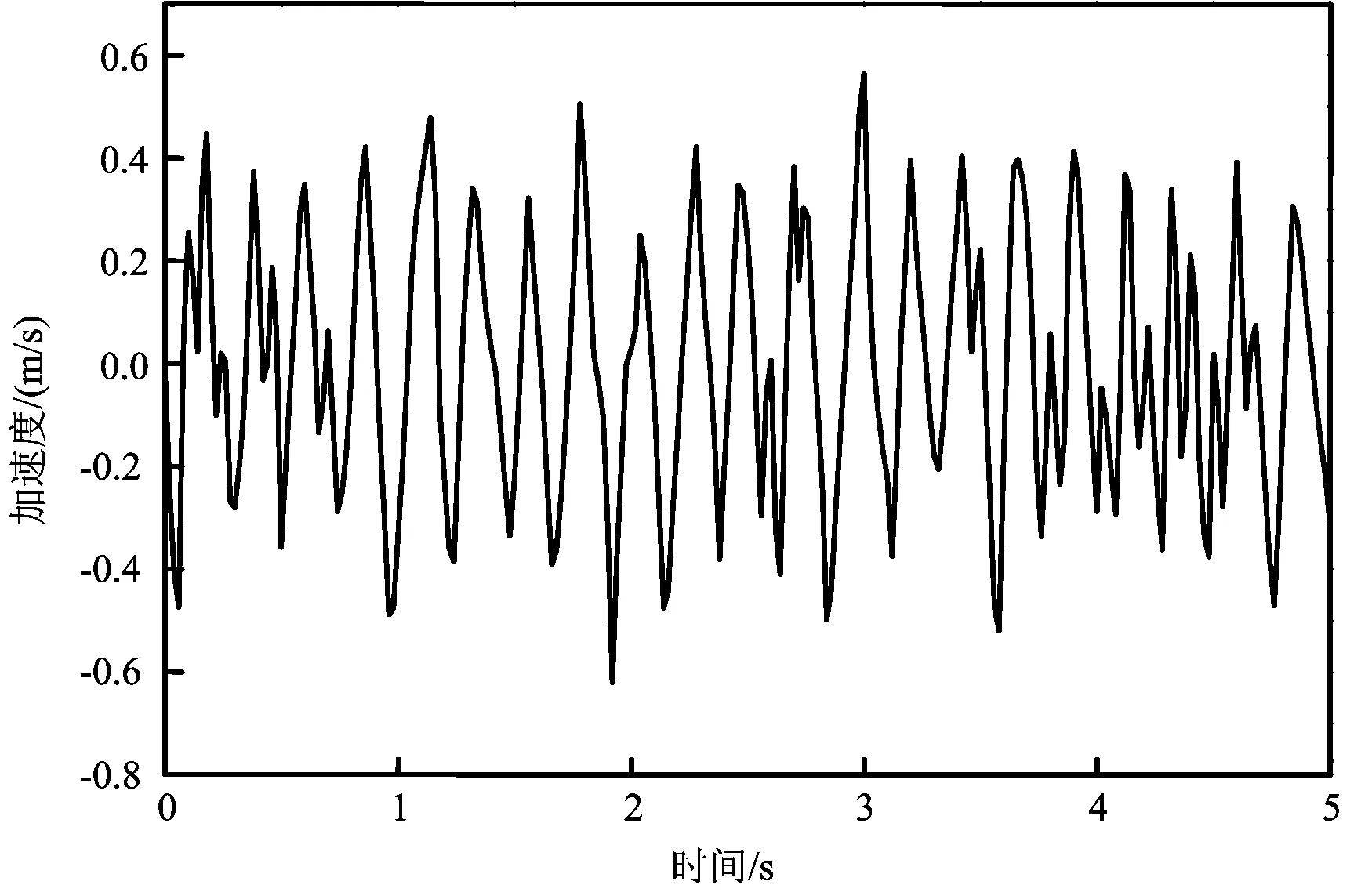
图1 激励加速度时程曲线

图2 无隔振措施计算模型图
2 计算结果
2.1 空沟隔振作用分析及对比参数工况设置
由于实际监测空冷岛上部振动超标主要为水平方向,为对比加隔振措施前后的空沟后土体以及空冷岛上部风筒梁的振动变化情况,主要分析考虑水平振动。为了说明空沟对其后距离振源固定位置处地面点的减隔振作用,图3给出了距生料磨基础20 m(即空冷平台底部)处地表一点,在未施加减隔振措施前和设置深10 m、宽0.5 m、距立磨基础边缘4 m的空沟后的水平加速度时程曲线对比。可见,相比于不加隔振措施,空沟后地表同一点处的加速度幅值显著降低,说明在生料磨与空冷岛之间设置空沟能够阻碍振动在土层中的传播。
为了探究深度、宽度和距离振源距离等对空沟隔振作用的影响,取空沟深度为5 m、10 m和15 m,宽度0.5 m、1 m和1.5 m,以及空沟距振源距离为4 m、10 m和16 m等几种工况,进行空沟隔振效果的对比分析,具体工况安排如表2。其中,根现场设备布置情况,模型中空沟沟长均取18 m。
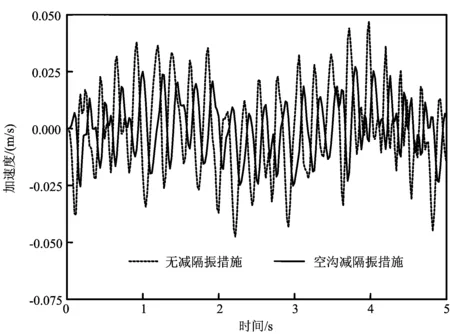
图3 距振源20 m处地表加速度时程对比
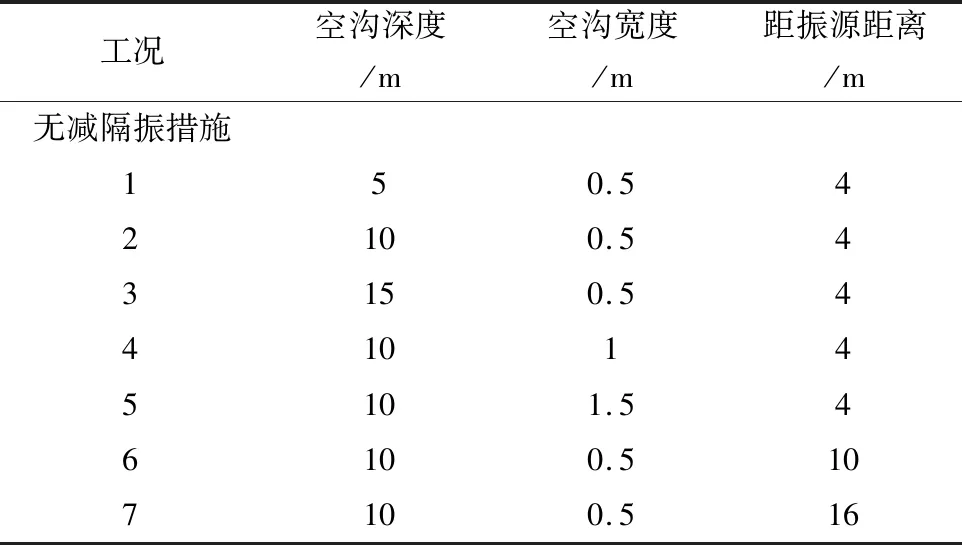
表2 空沟隔振计算工况列表
2.2 空沟深度对隔振作用的影响
为研究本隔振工程沟的深度对其隔振作用的影响,先固定沟宽为0.5m,空沟距振源距离为4 m,改变沟深度为5 m、10 m和15 m,对应表2中的工况1、2、3。分析时在空沟后侧至空冷岛底部每间隔1m取一个测点。
图4给出了不同深度工况下各测点的加速度峰值。可见,加空沟隔振措施后,其后各测点加速度峰值都有所降低。随着深度增大其加速度值降低的越多。在沟深小于5 m 时,沟后地表加速度峰值随空沟深度增大而迅速衰减,当沟深超过5 m后,随空沟深度的加深,各测点加速度峰值衰减程度逐渐放缓,但依然对振动衰减很有效。各深度工况都有在沟后5 m范围内的地面加速度峰值衰减较快,大于5 m以后加速度的衰减减慢的特征。
表3给出了不同沟深时空冷岛上部风筒梁振动的最大加速度和速度的比较,其中最大加速度相对值为加空沟隔振措施与无隔振时风筒梁最大加速度之比。相比于无隔振,当空沟深度为5 m、10 m和15 m时,风筒梁最大加速度分别衰减了17.74%、29.68%和33.87%。随着沟深的增加,空冷平台风筒梁振动加速度和速度衰减明显,当深度达到10 m时,风筒梁的最大振动速度值减小至5.92 mm/s,小于规定的最大限值6.3 mm/s,空冷岛风机可正常运行。综合计算结果与施工难易,可将空沟深度设置为12-15 m。
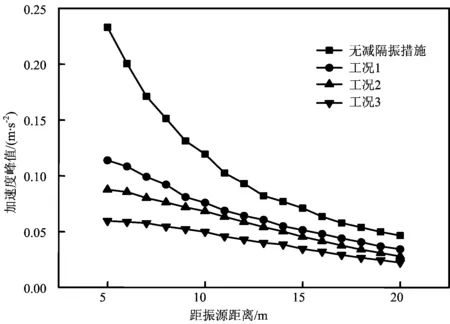
图4 深度对隔振作用的影响
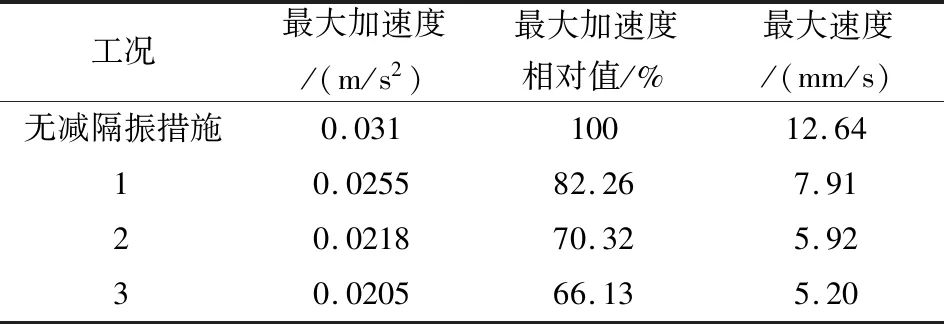
表3 不同空沟深度空冷岛风筒梁的最大加速度和速度比较
2.3 空沟宽度对隔振作用的影响
为研究空沟宽度对隔振作用的影响,固定空沟深度10 m,距振源距离4 m,改变空沟宽度分别为0.5 m、1 m和1.5 m,对应表2中工况2、4和5,空沟后侧至空冷岛底部每间隔1 m取一个测点。
图5给出了不同宽度时各测点加速度峰值,可见随着沟宽度的增加,各点加速度峰值变化很小,只在沟后5 m范围内有较小衰减。在空沟后大于5 m处,随沟宽度的增加,地表加速度峰值基本保持稳定,也就是说宽度改变对该范围以外的影响很小。
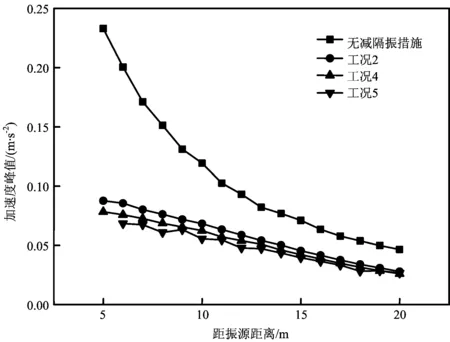
图5 宽度的影响
表4为不同空沟宽度时空冷岛上部风筒梁振动的最大加速度和速度的比较,对比加空沟之前,当设置沟宽为0.5 m、1 m和1.5 m时,风筒梁最大加速度分别衰减了29.68%、30.32%和30.65%。可见深度固定为10 m时,随着空沟宽度的增加,空冷平台风筒梁振动加速度和速度衰减变化很小,空沟宽度由0.5 m加大到1.5 m,风筒梁最大振动速度基本稳定在5.89 mm/s左右,小于规定的最大限值6.3 mm/s。综合计算结果及空沟的施工难易程度,可将空沟宽度设在1 m以内。
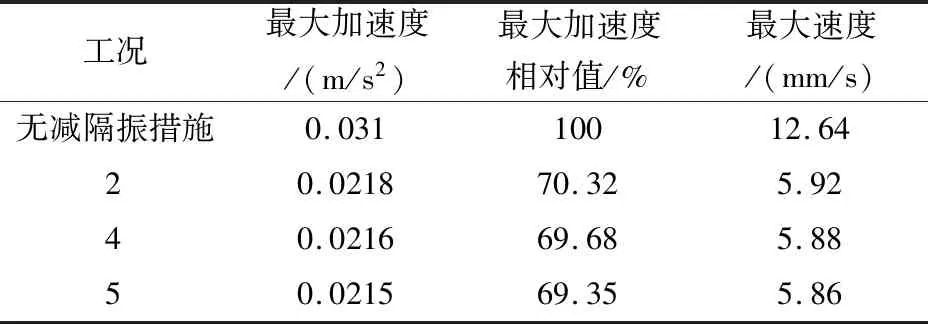
表4 不同空沟宽度空冷岛风筒梁的最大加速度和速度比较
2.4 空沟距振源距离对隔振作用的影响
为研究空沟距振源距离对其隔振作用的影响,固定沟深为10 m,宽度0.5 m,改变空沟距振源距离分别为4 m、10 m、16 m,对应工况2、6、7。空沟后至空冷岛底每隔1 m取一测点。
图6为空沟在不同距离时各测点加速度峰值。可见,空沟与振源间距离改变会影响隔振效果。随着空沟距振源距离的增大,各测点加速度峰值的衰减程度先减弱后又有所回升。
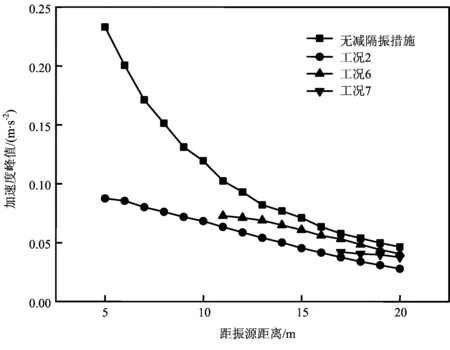
图6 空沟距振源距离的影响
表5给出了不同空沟距离条件下空冷岛上部风筒梁振动的最大加速度和速度的比较,与无减隔振措施相比,当空沟深度为10 m,宽度为0.5 m,距振源距离为4 m、10 m和16 m时,风筒梁最大加速度分别衰减了29.68%、22.58%和25.81%。可见随空沟距振源距离的增大风筒梁振动加速度和速度衰减呈先减弱后增强的趋势,但后两种工况风筒梁最大振动速度相差不大,都可超过最大限值6.3 mm/s。三种不同位置空沟隔振时,空沟设在距立磨基础4 m左右,隔振效果最好,本工程采用空沟减振措施时更适用于近源隔振。
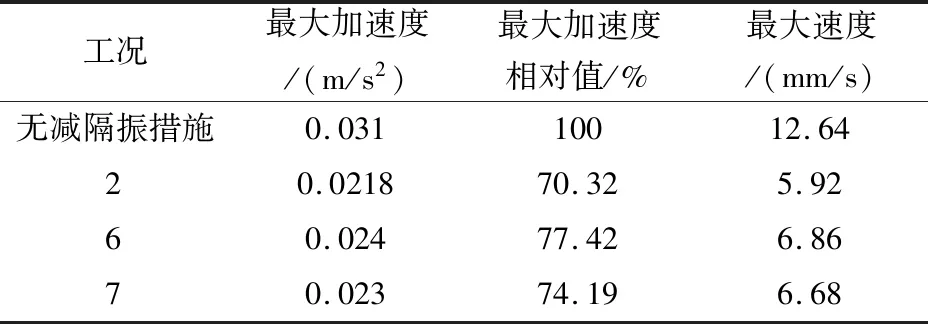
表5 不同空沟位置空冷岛风筒梁的最大加速度和速度比较
3 结 论
(1)空沟减振措施能够有效地解决生料磨诱发空冷平台振动问题,空沟的设置使沟后土体及空冷平台风筒梁的振动明显减弱。设置一定深度空沟可将空冷岛上部风筒梁的最大振动速度从12.64 mm/s降至5.2 mm/s,小于允许的最大限制6.3 mm/s。
(2)空沟的深度对其隔振作用影响很大,深度越大,隔振效果越好。但增加至一定深度后,其隔振效果增强幅度逐渐放缓。当设置空沟深度达10 m以上时,空冷岛风筒梁的最大振动速度可以达标。综合考虑空冷岛风机运行安全性与空沟的施工难易程度,可将空沟深度设置为12~15 m。
(3)空沟宽度对隔振作用的影响不明显,宽度的增加并不能很好的衰减沟后土体以及空冷平台风筒梁的振动,综合考虑空沟隔振效果与施工难度,可将空沟宽度取在1 m以内。
(4)空沟与振源的距离对隔振效果有较大影响。由计算结果可知,当空沟设置在距立磨基础4 m左右时,隔振效果最好,本工程空沟隔振措施更适用于近源隔振。为保证空冷岛风机运行安全性同时考虑实际施工难易程度,可将空沟深度设为12~15 m的同时尽量将其布置在靠近生料立磨一侧。
