基坑桩锚支护体系失稳破坏安全系数研究

2021-12-23江朋,王根

工程与建设 2021年5期

江朋,王根

(安徽省交通规划设计研究总院股份有限公司,安徽合肥 230088)

0 引言

基坑支护有多种形式,桩锚支护体系是其中常用的一种支护形式[1]。随着大量深基坑的出现,稳定性是基坑工程中要面临的巨大挑战[2]。目前,设计中用于评估基坑失稳破坏安全系数的方法主要有圆弧滑动条分法、Kranz法及强度折减有限元法。但是由于这三种方法侧重于不同的失稳机理,各自均具有一定的局限性及风险性,从而导致基坑工程中出现过很多重大事故。如新加坡Nicoll Highway地铁车站[3]的在设计基坑支护体系时安全系数评估满足规范要求,但基坑在开挖至坑底时却出现了倒塌的现象;上海地铁9号线的上城路地铁车站[4],其基坑支护体系的设计安全系数远远满足规范要求,但是开挖到18m时同样出现了基坑破坏的现象。因此,如何正确合理的选择这三种方法来评估基坑的稳定性显得非常重要。

目前学者们桩锚支护体系的整体失稳主要有两种形式[5],第一种是由于土体自重过大,引起围护结构后的土坡及支护结构共同发生滑动,从而导致基坑发生稳定性破坏,此即为圆弧滑动条分法所基于的基坑破坏机理;第二种是认为锚杆的自由段长度过短导致锚杆发生破坏,从而导致基坑发生稳定性破坏,此即为Kranz法所基于的基坑破坏机理。圆弧滑动条分法[6]是目前基坑工程应用最为广泛的一种方法,但是该方法仅能满足滑动土体的整体力矩平衡而不满足其它平衡条件,从而用于预测基坑的稳定性时具有一定的局限性。Kranz法[7]是德国学者提出的“代替墙法”,开始被欧洲规范所使用,现在在我国也有了较大的影响,但是规范及众多学者对KRANZ法的理解有较大的不同。此外Kranz法只适用于均质土层,当应用于复杂土层时,需要进行很多简化处理,所以用于基坑设计时也具有一定的局限性。强度折减有限法[8]最先由Zienkiewicz提出并应用于边坡的失稳破坏安全性分析,目前很多学者及设计者也渐渐利用此方法来预测基坑的稳定性。但是,由于边坡稳定性分析中只将强度折减用于土体参数中,而基坑桩锚支护体系中除了土体参数外,如何对土体-锚杆间的强度进行折减也需要进行研究和探讨。

本文详细地介绍了圆弧滑动条分法、Kranz法及强度折减有限元法的计算过程,并对基坑的失稳破坏安全系数进行了分析和比较。

1 基坑桩锚支护结构嵌固深度可靠度分析模型

1.1 圆弧滑动简单条分法

图1所示为一典型基坑桩锚支护体系,H为基坑深度,h为围护桩锚固深度。根据规范[9],圆弧滑动简单条分法是基坑支护体系稳定性分析最常用的方法。具有以下的假定及计算工程:

(1)假定支护体系的失稳破坏面为圆弧形式;

(2)将圆弧破坏面以内的破坏体划分成若干等宽度的竖直土条;

(3)忽略了土条间的相互作用力;

(4)破坏面上土体的抗剪强度由摩尔-库伦破坏准则确定;

(5)当锚杆穿过圆弧破坏面时,需要考虑锚杆拉力对滑动土体的作用力;

(6)根据作用力形式分别计算得到抗滑力矩和和滑动力矩;

(7)搜素所有经过桩底及其桩底以下的圆弧破坏面,并假定划分土条宽度,从而确定各圆弧破坏面对应的安全系数,最小安全系数即可认为是此支护体系的整体稳定性安全系数,而最小安全系数对应的圆弧面即为该支护体系的实际破坏面。

如图1所示,第j条土条的自重Wj为:

Wj=γjbjhj

(1)

式中:rj为第j个土体容重;bj为第j个土条的宽度;hj为第j个土条的高度。

第j个土条底面上的法向反力Nj及抗剪强度Sj为:

Nj=(Wj+qjbj)cosθj-μjbj

(2)

Sj=cjlj+[(Wj+qjbj)cosθj-μjbj]tanφj

(3)

式中:qj为第j个土条上的超载强度;θj为第j个土条滑弧面处的法线与竖直方向的夹角;μj为第j个土条的孔隙水压力;cj、φj分别为第j个土条的黏聚力及内摩擦角;lj为第j个土条的底面滑弧长度,lj=bj/cosθj。

因此,所有土条的滑动力矩Ms为:

(4)

所有土条的抗滑力矩Mr为:

(5)

式中:R为圆弧破坏面的半径;θsk为滑弧面在第k层锚杆处的法线与垂直面的夹角;βk为第k层锚杆的倾角;sk为第k层锚杆的水平间距;Rk为第k层锚杆极限抗拔承载力,可由下式计算得到:

(6)

其中:d为锚杆锚固段直径;qsk,i为第k层锚杆与第i层土体的极限粘性强度;lski为第k层锚杆的锚固段在第i层土体的长度。

因此,基坑的整体稳定性安全系数fs为:

(7)

当考虑土层均质、均匀超载及单锚杆支护时,基坑的整体稳定性安全系数fs可简化为:

(8)

图1 圆弧滑动简单条分法示意图

1.2 Kranz方法

Kranz失稳形式为当桩锚支护体系之间的相互作用超出了土体的承载能力,从而在围护桩结构底部向其拉结方向形成一条深层滑裂面。如图2所示,假定深层滑裂面由直线bc段和cd段组成,其中b点取在围护桩底部,c点取在锚固段的中点,cd段是由c点向上做垂线与地面交于d点得到。安全系数定义为锚杆极限抗力的水平分力Th与锚杆设计水平分力Tsh的比值。

由图2可知,锚杆极限拉力水平分力可以从力的平衡图得到:

Th=E1h-E2h+Qh

(9)

E1h=E1cosδ

(10)

E2h=E2cosδ

(11)

Qh=(W+E2htanδ-E1htanδ)tan(φ-θ)-Thtanαtan(φ-θ)

(12)

式中:E1为作用在围护结构ab面上的主动土压力;E2为作用在代替墙cd面上的主动土压力,E1、E2可采用库伦主动土压力公式计算得到;δ为墙面摩擦角;φ为土体的内摩擦角;θ为代替墙bc与水平面的夹角;α为锚杆的倾斜角;W为土体abcd的重量。

由式(9)～(12)整理可得:

(13)

图2 Kranz提出的“代替墙法”

1.3 强度折减有限元法

利用强度折减有限元法进行基坑桩锚支护体系稳定性分析时,需要作出以下三个基本假定:(1)土体抗剪强度指标c、φ的折减不会影响其他的土体特性参数;(2)c、φ对土体抗剪强度同等重要,因此强度折减时对c、φ作出同等程度的折减;(3)除了岩土体抗剪强度指标,锚杆与土体间的极限粘结强度作出同等程度的折减。此外,在折减有限元计算过程中,可得到如图3所示的典型节点位移-强度折减系数SRR关系曲线,即当强度折减系数SRR增大到一定值时,有限元典型单元节点位移开始急剧增大,此时数值计算结果将会出现计算不收敛的情况[10],此曲线单元节点位移转折点所对应的强度折减系数SRR可认定为该基坑的稳定性安全系数FOS。

图3 典型节点位移与折减系数关系曲线

2 典型工况计算对比

2.1 参数取值

为了计算方便,本文考虑土层均匀且无地下水,分析了单锚支护这种支护体系。基本参数如表1。

表1 支护体系基坑主要参数

2.2 PLAXIS 2D数值模型

本文采用了有限元软件PLAXIS 2D建立了数值模型模拟了基坑开挖过程,图4为数值分析模型。数值分析模型中土体采用摩尔-库仑(MC)本构模型。

图4 基坑有限元模型及网格划分

2.3 基坑安全系数与锚杆长度的关系分析

图5给出了当锚杆锚固段长度为6 m时,不同锚杆自由段长度下分别利用圆弧滑动条分法、Kranz法及强度折减有限元法得到的安全系数。由图5可知,当锚杆自由段长度由5 m加大到10 m时,三种安全系数分别增大了0.026、2.239、0.959。圆弧条分法安全系数及Kranz法安全系数的变化趋势与其假定的基坑破坏机制相吻合,故均具有一定的局限性。强度折减有限元法安全系数先显著增大,后趋于平缓,变化趋势较为合理。因此,当锚杆自由段长度较小时,应该利用Kranz法验证基坑的稳定性;而当锚杆自由段长度较大时,应该利用圆弧条分法验证基坑的稳定性。而强度折减有限元法计算结果较为合理,在基坑设计中具有一定的参考价值,可以与圆弧条分法或Kranz法相结合来指导基坑的设计。

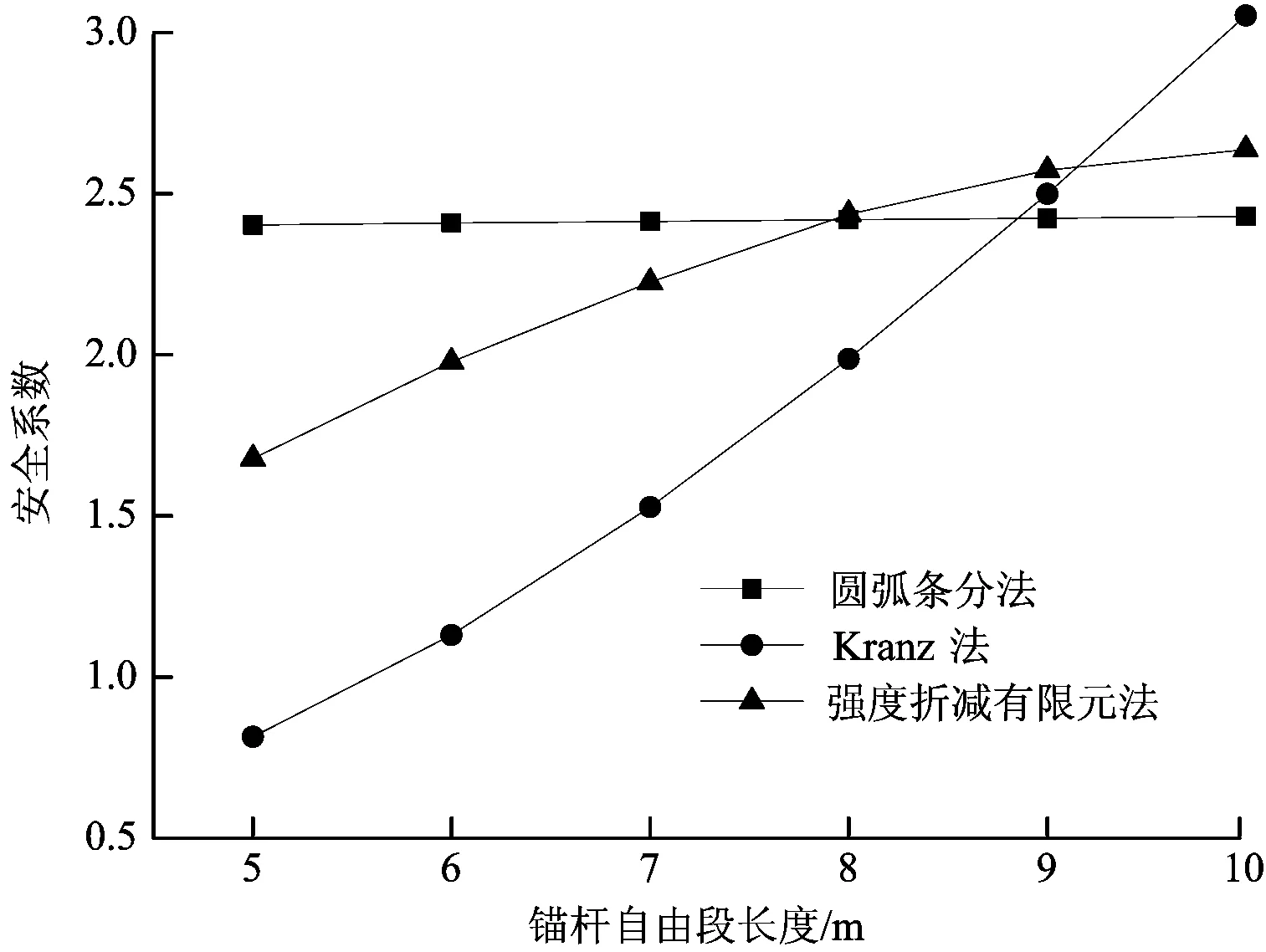
图5 锚杆自由段长度与基坑安全系数的关系曲线

图6给出了当锚杆自由段长度为5 m时,不同锚杆锚固段长度下分别利用圆弧滑动条分法、Kranz法及强度折减有限元法得到的安全系数。当锚固段由6 m增大到11 m时,三种安全系数分别增大了0.034、0.141、0.996。相较于自由段,锚固段长度对三种安全系数的影响均较小。因此,锚杆的自由段长度是影响基坑安全系数的重要因素。

图6 基坑安全系数与锚杆锚固段长度的关系曲线

4.3 基坑安全系数与围护桩锚固深度的关系分析

当锚杆自由段长度为9 m、锚固段长度为6 m时,不同围护桩嵌固深度下分别利用圆弧滑动条分法、Kranz法及强度折减有限元法得到的安全系数如图7所示。由图7可知,当围护桩嵌固深度由3 m增大到7 m时,三种安全系数分别增大了0.509、2.338、1.334。由三种安全系数对比可知,当围护桩嵌固深度较小时,应该利用Kranz法验证基坑的稳定性;当围护桩嵌固深度较大时,应该利用圆弧滑动条分法来验证基坑的稳定性。此外,强度折减有限元法安全系数趋于Kranz法安全系数及圆弧条分法安全系数之间,具有一定的合理性,在基坑设计时应该结合强度折减有限元法来指导设计。