钢管混凝土系杆拱桥的初张力优化研究

朱龙龙

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引 言

在大跨钢管混凝土系杆拱桥施工中,吊杆张拉时会对相邻吊杆也产生影响。不同位置吊杆张拉对临近吊杆索力值的影响的程度大小也有差异,这往往会导致在桥面铺装等二期恒载施工后,吊杆初张拉后在该工况产生的索力值与设计成桥索力值之间往往存在较大的误差,因此通常都要经过二次调索来达到设计成桥索力[1]。

确定合理的吊杆初张力在桥梁施工过程中非常重要,合理的吊杆初张力能够保证施工过程中的桥梁结构处于安全、合理的受力状态。目前常用的确定初张力的方法有倒拆法、影响矩阵法、正装迭代法、无应力状态法等优化方法[2]。

本文研究目的在于采用影响矩阵法及无应力状态法来进行吊杆初张力优化,尽量使其通过一次初张后的二期恒载状态下的索力值与设计成桥索力值相比,误差在控制范围内,以减少二次调索施工。

1 施工阶段索力优化方法

1.1 影响矩阵法

影响矩阵法是以每根吊杆的索力值为基本未知量,通过给吊杆施加单位力,利用有限元模型求出单位力作用下吊杆索力影响矩阵，建立典型方程，然后通过求解线性方程组得到每根吊杆的索力值,最终使二期恒载状态下吊杆的索力值达到规定的设计值[3]。

(1)以设计初张力{N0}得到二期恒载索力{T0},设计成桥索力为{F0},{F0}与{T0}之间差值为:

{δ0}={F0}-{T0}

(1)

(2)根据吊杆设计张拉顺序,对每根吊杆均施加单位索力f,得到索力影响矩阵[A]。

(2)

式中:aij表示第j号吊杆施加单位索力时对第i号吊杆索力影响量。

(3)得到吊杆索力调整值为:

{X}=[A]-1{δ0}

(3)

(4)假设用该二期恒载状态下的索力调整值来修正吊杆初张力,即有:

{N1}={N0}+{X}

(4)

(5)用修正后的吊杆初张力按原张拉次序进行模拟计算,得到新的二期恒载索力{T1}。将{T1}与设计成桥索力{F0}进行比较,检验是否满足精度要求。

(6)如果不满足精度要求,则将{T1}代入式(1),重新按工序进行张拉模拟分析,直至精度满足要求为止。

1.2 无应力状态法

无应力状态法指出对于相同的结构,当其边界条件、外荷载、单元的无应力长度相同时,则成桥状态下的结构内力和位移是唯一的。结构单元的内力状态、位移状态会随着索力的变化而变化,但吊杆的无应力长度只有在其主动张拉时才会发生变化,即主动张拉的单元其无应力长度发生改变,但不会改变其他未主动张拉单元的无应力长度[4]。

无应力长度即吊杆的实际几何长度减去吊杆的弹性变形量。假设吊杆截面面积为A,弹性模量为E,吊杆索力为N,则索力产生的变形量为:

(6)

无应力长度为:

L0=L-ΔL

(7)

实际施工中吊杆无应力长度的调整可以通过千斤顶的张拉,用锚头处的拔出量来控制,也可以将其转变为索力的变化量来控制。由于荷载和结构体系一定时,索力的增量与其无应力长度的变化存在一一对应关系[5]。假设当吊杆初张力为T1时,其无应力长度为L01,当初张力变为T1+ΔT时,其无应力长度为L02,可得当初张力变化ΔT无应力长度的变化为L02-L01,由此根据每对吊杆在初张拉时的空间位置来计算实际初张力,从而使初张拉后的无应力长度为成桥状态下的无应力长度,即可完成初张力优化[7]。

2 计算实例分析

2.1 工程背景

某下承式钢管混凝土系杆拱桥,计算跨径为128 m,桥面宽度为13.2 m;系梁按整体箱形梁布置,拱肋采用悬链线线型,拱肋横截面采用哑铃形钢管混凝土截面,钢管直径为1.2 m,上、下钢管及腹腔均为钢混组合结构。全桥共设置5道K字横撑。MIDAS模型如图1所示,模型共有592个单元和672个节点。系梁及拱肋的施工工艺为支架浇筑和安装。

图1 钢管混凝土系杆拱桥模型

2.2 影响矩阵法吊杆初张力优化

此系杆拱桥共28对吊杆,采用对称张拉,可简化为14组,从拱脚到拱顶由短到长依次编号为1-14。按照设计要求,吊杆张拉顺序为2-4-6-8-10-12-3-5-7-9-11-13-14-1。具体施工工序见表1。

根据本文提供的计算方法,得到吊杆索力影响矩阵A为:

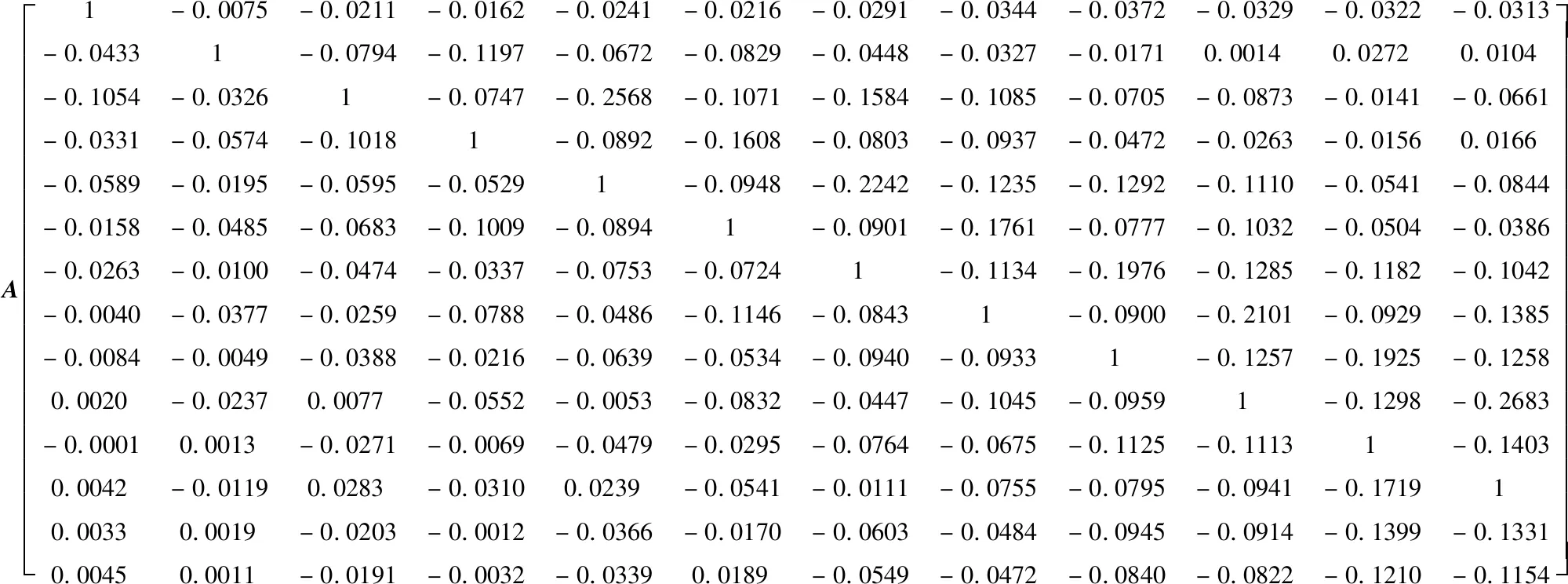
由索力影响矩阵可以明显看出,当张拉某对吊杆时,其临近的吊杆索力值均会减小,而较远处的吊杆索力值会增大一些。通过影响矩阵法优化后的吊杆初张力结果见表2。

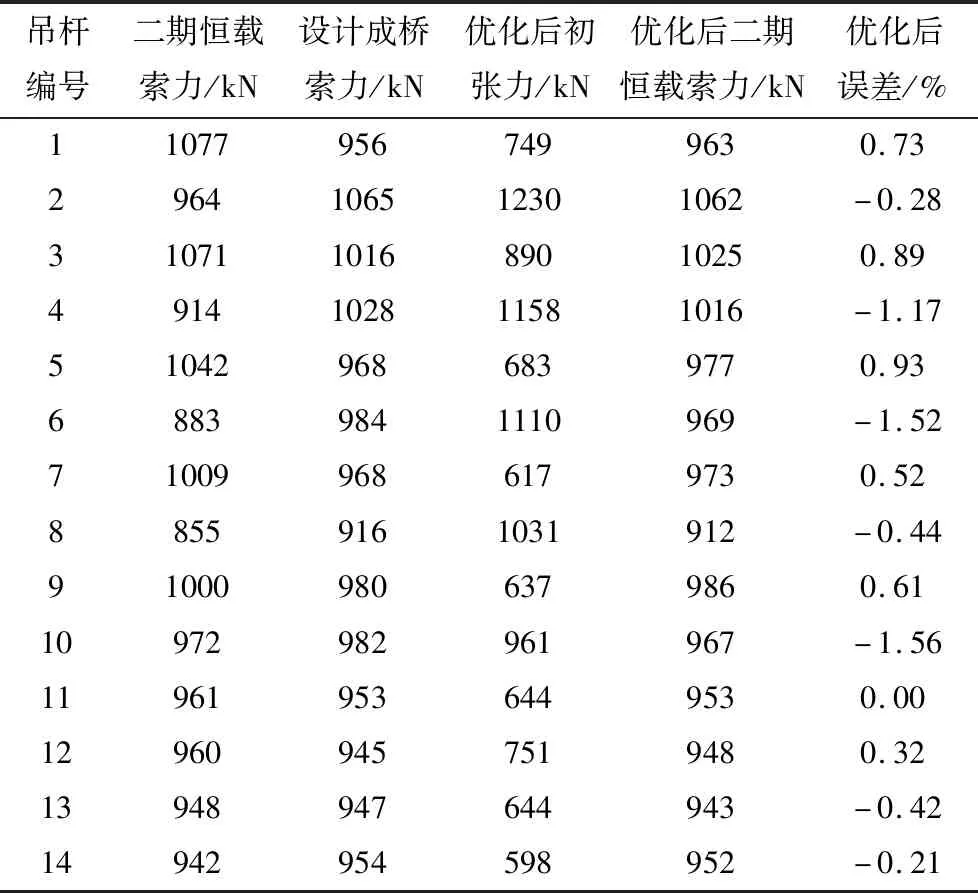
表2 影响矩阵法吊杆初张力优化

从表2可知,根据设计初张力及张拉次序得到的二期恒载状态下的索力值,与设计成桥索力值误差较大,而优化后二期恒载状态下的索力值与设计成桥索力值最大误差为1.56%,满足施工规范要求的误差5%以内的控制要求。

2.3 无应力状态法吊杆初张力优化

按设计初张力得到的二期恒载状态下吊杆的无应力长度,将之与设计成桥状态下无应力长度进行比较,结果见表3。

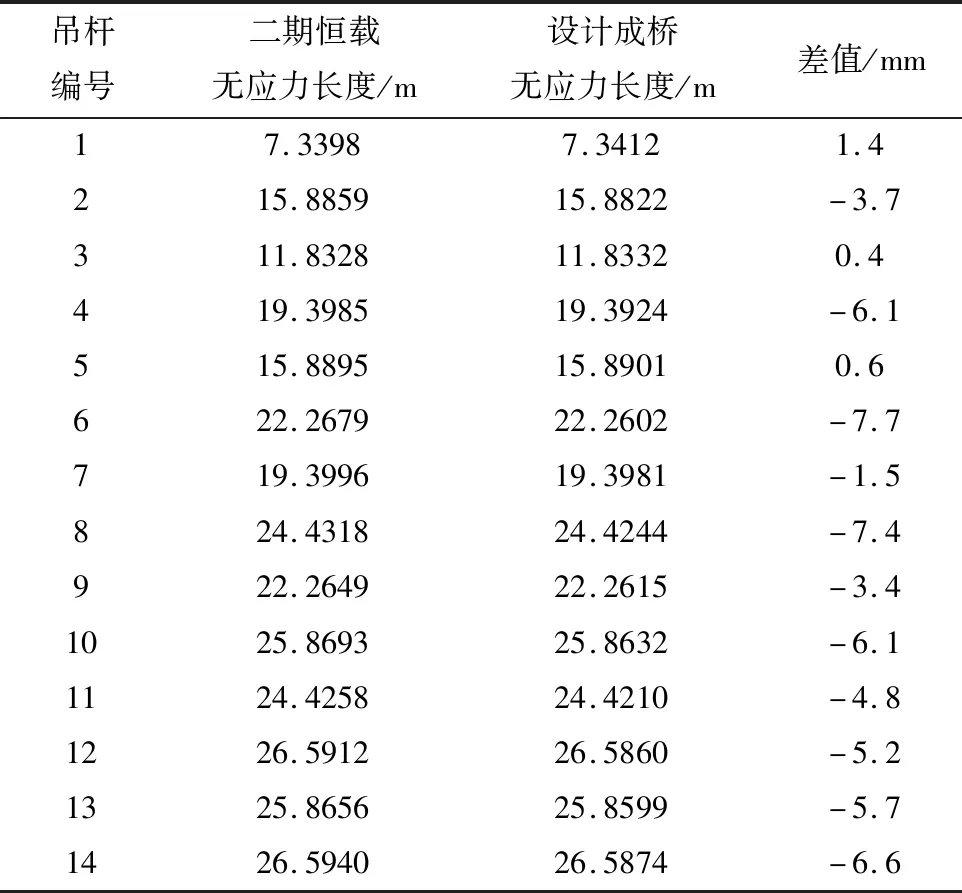
表3 吊杆无应力长度对比

从表3可知,无应力长度最大差值为7.7 mm,同样可根据无应力状态法对吊杆初张拉时的无应力长度进行调整,使各吊杆在初张拉后的无应力长度即为设计成桥状态下无应力长度。通过对每根吊杆施加单位索力得到无应力长度变化量,以此进一步得到具体的索力调整值[5]。初张力优化后得到的二期恒载状态下的吊杆索力值与设计成桥索力值最大误差为1.45%,具体结果见表4。

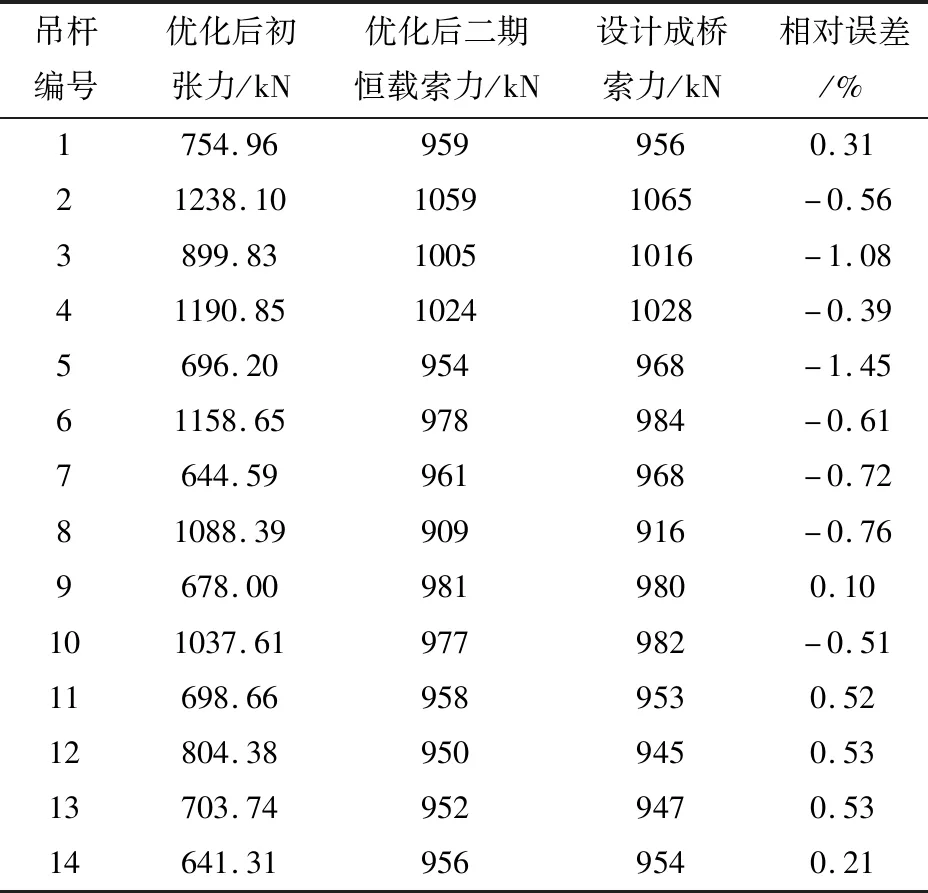
表4 无应力状态法吊杆初张力优化

从表2和表4所示的结果可以看出:基于影响矩阵法和无应力状态法计算得到的二期恒载状态索力与设计成桥索力的差值均比较均匀,误差控制满足规范要求。

2.4 优化初张力对施工影响分析

初张力调整必然对施工过程中的结构产生影响,为此进一步选取系梁及拱肋的几个控制截面对比分析初张力优化后对施工过程中截面应力变化的影响,以验证调整优化的可行性。

取系梁跨中截面,其应力变化比较结果如图2所示。

取拱肋钢管跨中截面,其应力比较结果如图3所示。

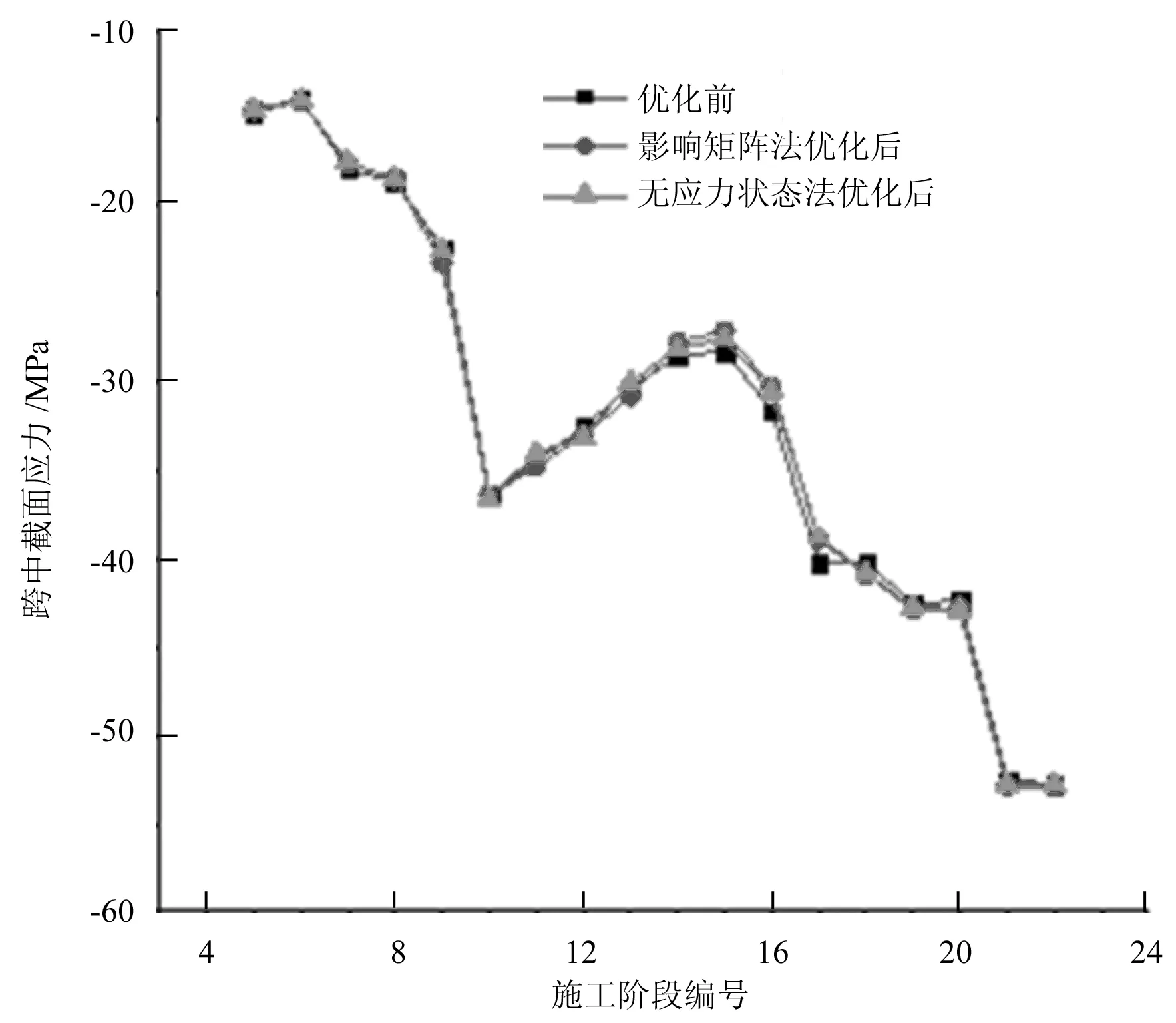
图3 拱肋钢管截面应力

分析图2、图3可知,优化后的初张力对结构的应力变化影响较小,能够保证结构安全,优化调整的初张力满足应力控制要求。

3 结 论

本文对系杆拱桥的施工初张力进行优化分析,可以得到以下结论:

(1)比较可以看出,无应力状态法的优化值比影响矩阵法优化后的成桥误差更小一些,当然这与影响矩阵法仅经过一次优化有关。

(2)可以用影响矩阵法和无应力状态法来调整吊杆的初张力,从成桥索力和控制截面应力变化的比较分析看,优化后施工是有安全保证的,吊杆的成桥索力能够较好地满足设计要求。

本文的初张力优化可为同类项目的施工控制提供参考。