一道椭圆方程题的求解思考

曹晓琰

(江苏省南京市中华中学 210019)

一、问题呈现

图1

二、问题分析

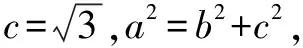
三、破解方向

点评根据条件可知PO为线段F1F2的中线，而与中线密切联系的就是平面向量知识，借助平面向量的线性运算、数量积等，就可以非常有效地构建起与中线有关的关系式，从而得以巧妙破解.

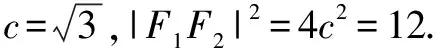
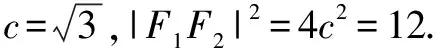
点评根据条件可知PO为线段F1F2的中线，把问题放在△PF1F2中来处理，其实质就是解三角形问题，借助三角形的性质，通过三边以及中线PO的条件，可以利用在两个不同三角形中同角的余弦值相等，或是两个不同三角形中互补角的余弦值互为相反数来建立有关的关系式，从而得以巧妙破解.

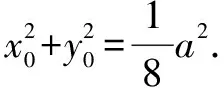
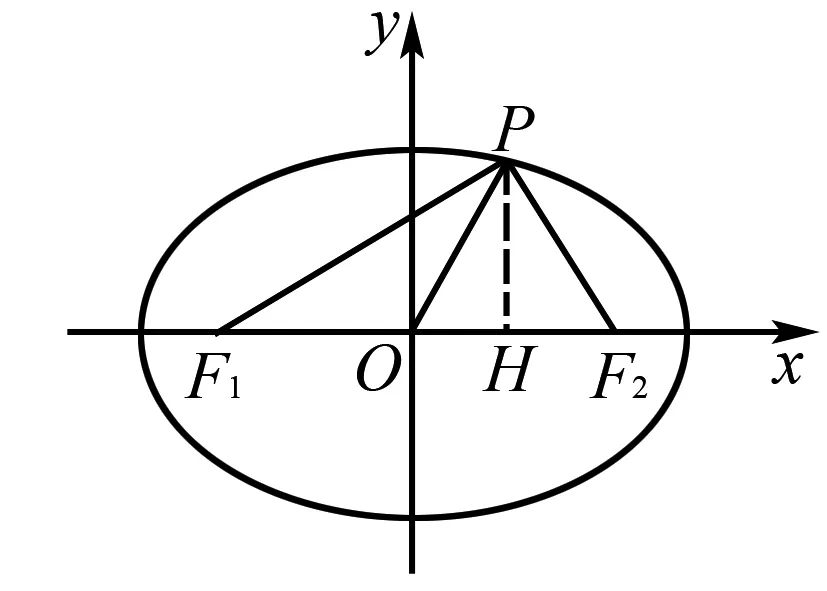
图2

①

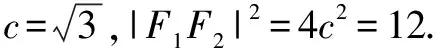
②

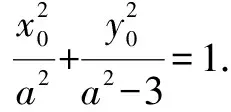
③

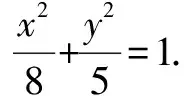
点评根据条件可知PO为线段F1F2的中线，又由|PF1|，|F1F2|，|PF2|成等比数列，可得|PF1|·|PF2|=|F1F2|2=12，涉及|PF1|与|PF2|的长度问题，可以考虑利用椭圆的几何性质，结合焦半径公式(|PF1|=a+ex0，|PF2|=a-ex0)加以转化，再结合题目相关条件建立有关的关系式，从而得以巧妙破解.

其实，在实际求解椭圆的标准方程中，一定要充分抓住椭圆的几何性质，根据具体情况选取比较合适的求解方法加以处理，有时也结合椭圆的几何性质、平面几何性质、平面向量、三角函数、解三角形、直线与圆等相关知识加以融合与交汇，利用相交知识的转化与应用来综合处理相应的方程问题.