稳健估计在地铁沉降监测数据处理中的应用
2021-12-23陈志江杨久东张凌云
陈志江,杨久东,张凌云
(华北理工大学 矿业工程学院,河北 唐山 063210)
随着城市不断发展,出行方式上越来越多样化,地铁交通也成为人们出行方式之一。在城市地铁施工中,不可避免地受到温度、压力等影响,对基坑周围产生沉降变形[1],这些形变对生产施工带来安全隐患,因此,获取连续监测变形数据对合理判断和预判地铁沉降至关重要。为了满足城市地铁的建设,许多学者对于深基坑变形规律和安全稳定性开展了大量的研究。王兴使用变形监测数据,运用传统模型数值分析、神经网络预测模型、灰色系统理论以及时间序列分析几种方法的对比与分析,进行基坑变形的预测[2]。唐永泽等针对深圳某大厦基坑工程,研究复杂条件的环境下深基坑对周围环境的影响,为工程施工和监测提供基础[3]。张永超等运用非等时距灰色预测数学模型,对基坑监测数据进行分析和检验[4]。任丽芳等和徐志彪基于ELM神经网络模型和土体损伤模型对基坑变形开展预测研究[5,6]。
在沉降监测过程中,采取任何高精度水准仪器或者测量方式,其观测数据中可能会存在由于多种原因造成的粗差,例如观测者操作不当、仪器出现故障、观测条件不利等因素。在含有粗差的数据处理中,使用最小二乘方法不可避免将粗差带入计算中从而导致整体计算的准确性[7],对实际施工造成误判。所以需要使用稳健估计的方法,把观测数据中粗差剔除,对数据处理不产生影响。该研究采用最小二乘法和稳健估计法2种不同的数据处理方法,对比存在粗差和不存在粗差的数据进行分析,验证稳健估计的抗差效果的优越性[8-10]。
1研究方法和理论
在地铁的施工测量时,观测时系统误差与偶然误差是不可避免的,除此之外,还常有忽略的粗差,如由于外部条件的干扰和外部条件的改变,测量人员的疏忽等原因造成的粗差,如果不剔除这些粗差,直接对其进行平差处理,一定会对数据处理与分析产生影响。为了降低、剔除粗差对数据处理的影响,在数据处理中选择一些算法对粗差进行处理,获得尽可能接近真实测量的有效估计。
1.1 回归分析
在建立线性回归分析模型时,首先将数据中因变量y和自变量x1,x2,…,xn分为两组,因变量y和自变量xn之间存在一定的函数关系[11],如果因变量y和自变量xn之间为线性关系,即:
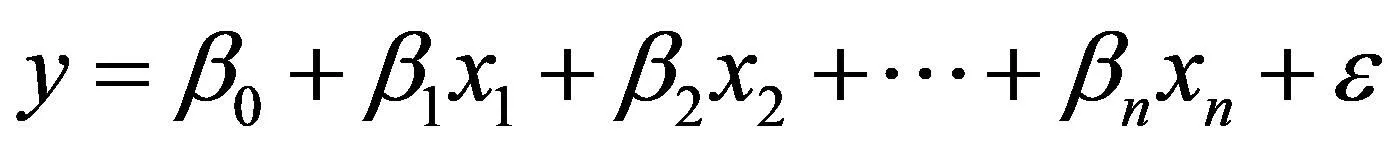
(1)
在式(1)中,β1、β2、…、βn为回归系数,β0为回归方程常数项,ε为随机扰动项,其数学期望为0。
1.2 最小二乘原理
最小二乘估计法:通过最小化误差的平方求和,寻找数据的最佳函数拟合。利用最小二乘估计法可以快速地求出未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小[12]。
函数模型:
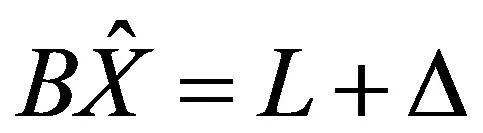
(2)
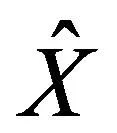
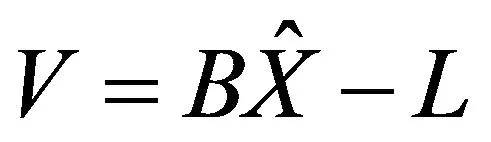
(3)
最小二乘平差准则就是:
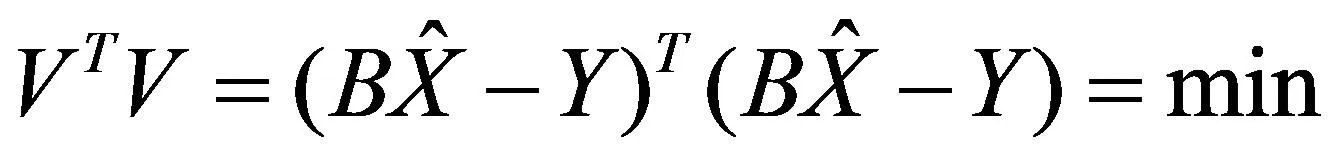
(4)
根据上式可得最小二乘解:
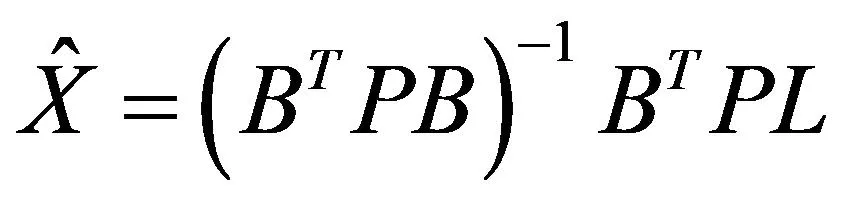
(5)
1.3 稳健估计原理
在粗差无法避免的情况下,选择合理的估计模型,使参数估值尽量避免由观测数据粗差所带来的偏离真值,得到一般情况下最优参数估计,参数估计的原则是充分利用观测数据中有效的数据信息,排除或者降权无效或有害信息,由于事先不知道具体观测数据中有效信息和无效信息的分布情况,所以在数据处理上,采用抗差的方法,为了获取一些可靠的、具有实际意义的有效估值,舍弃一部分观测粗差[13,14]。
稳健估计平差准则:
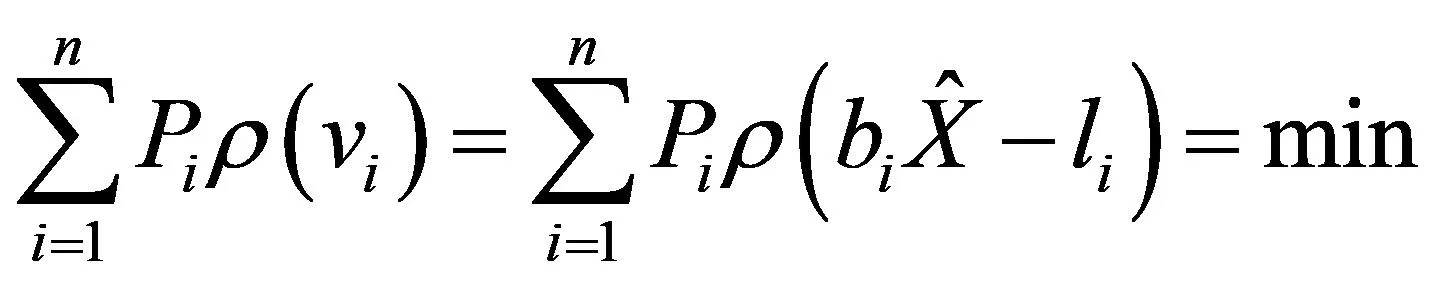
(6)
稳健估计解:
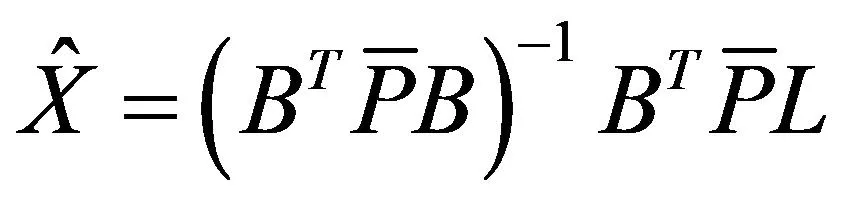
(7)
本文采取的是Andrews法:

(8)

3案例分析
3.1 数据采集
为了验证稳健估计数据处理的可行性,现以深圳市某地铁的基坑沉降点高程监测数据为参考,鉴于文章篇幅限制,只截取2019年9月1日至12月1日DB-11-01监测点号观测数据,以周为单位,总共14个周报数据,地铁沉降点DB-11-01监测数据如表1所示。利用截取14个周报观测数据进行最小二乘和稳健估计模型拟合,通过拟合模型分析数据异常的具体原因。

表1 DB-11-01沉降点监测数据
3.2 实验对比分析
3.2.1不含粗差的数据分析
利用MATLAB软件,分别使用最小二乘法和稳健估计,将外业采集到的水准沉降数据进行回归分析。
通过图1原始数据残差图可以看出,14个观测数据误差都在允许的范围内,不存在明显粗差。
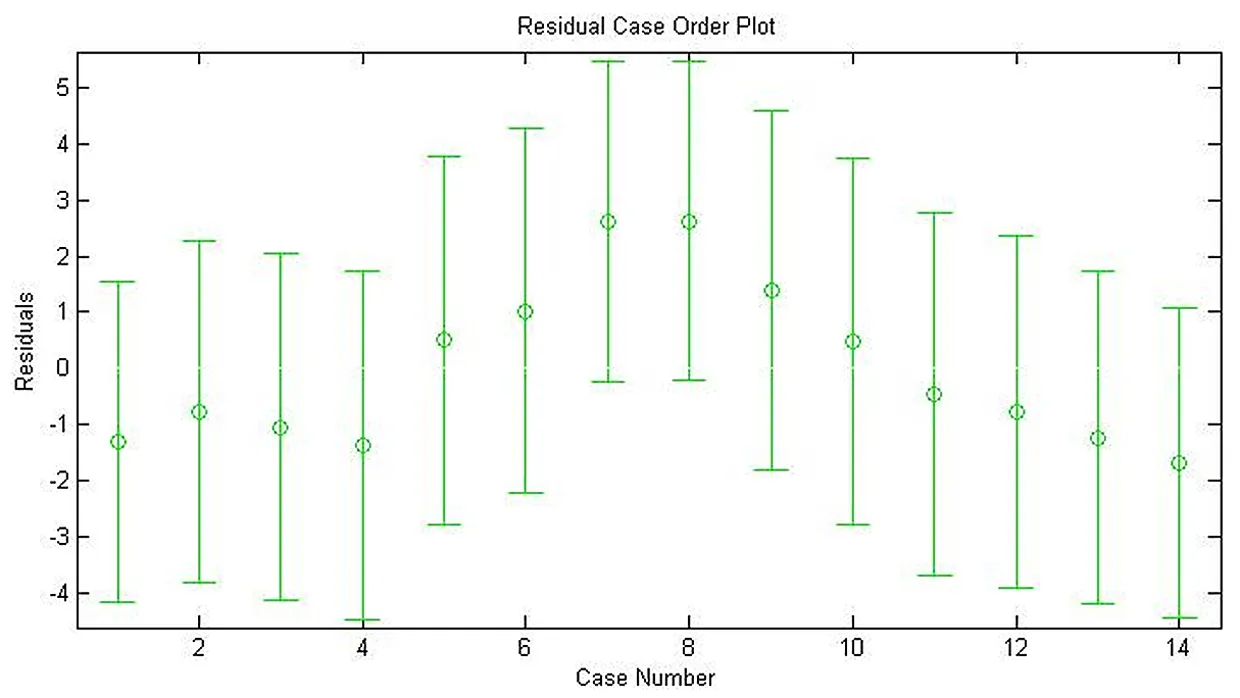
图1 原始数据残差图
利用最小二乘法得到的一元方程系数b0=-1.317 7,b1=-0.190 4,故最小二乘法得到的一元线性回归方程为:
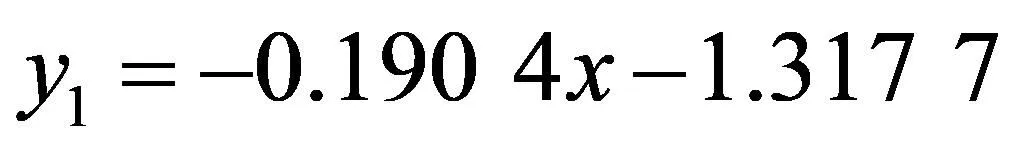
(9)
同理利用稳健估计回归分析得到一元线性回归方程系数b2=-1.317 6,b3=-0.190 4,故稳健估计法得到的一元线性回归方程为:
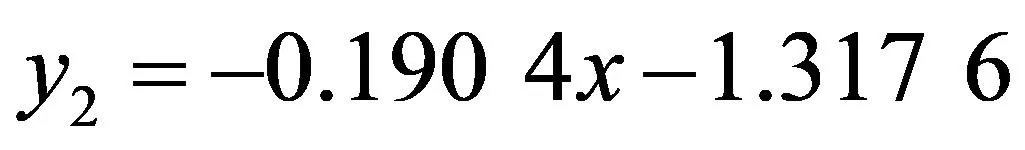
(10)
图2所示为无粗差下2种不同方法拟合方程图:
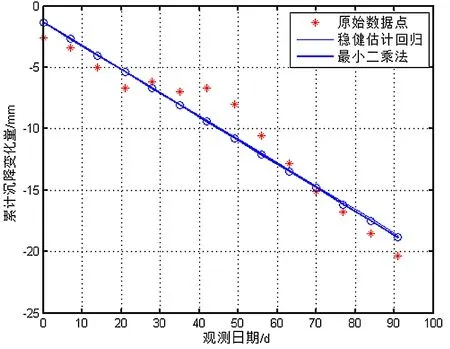
图2 无粗差2种不同方法拟合方程图
通过计算可以得出,在观测数据不存在粗差的情况下,2种方法方程几乎一样,其中1.460 0、1.519 6分别表示使用最小二乘法、稳健估计分析的中误差,采用最小二乘法和稳健估计法计算残差平方和均为27.709 2,说明在不存在粗差的情况下,最小二乘和稳健估计拟合效果相差不大。
3.2.2含粗差的数据分析
将外业2019年12月1采集到的数据认为加入粗差,原始观测-20.33修改为-24.33,处理后的残差图如图3所示:
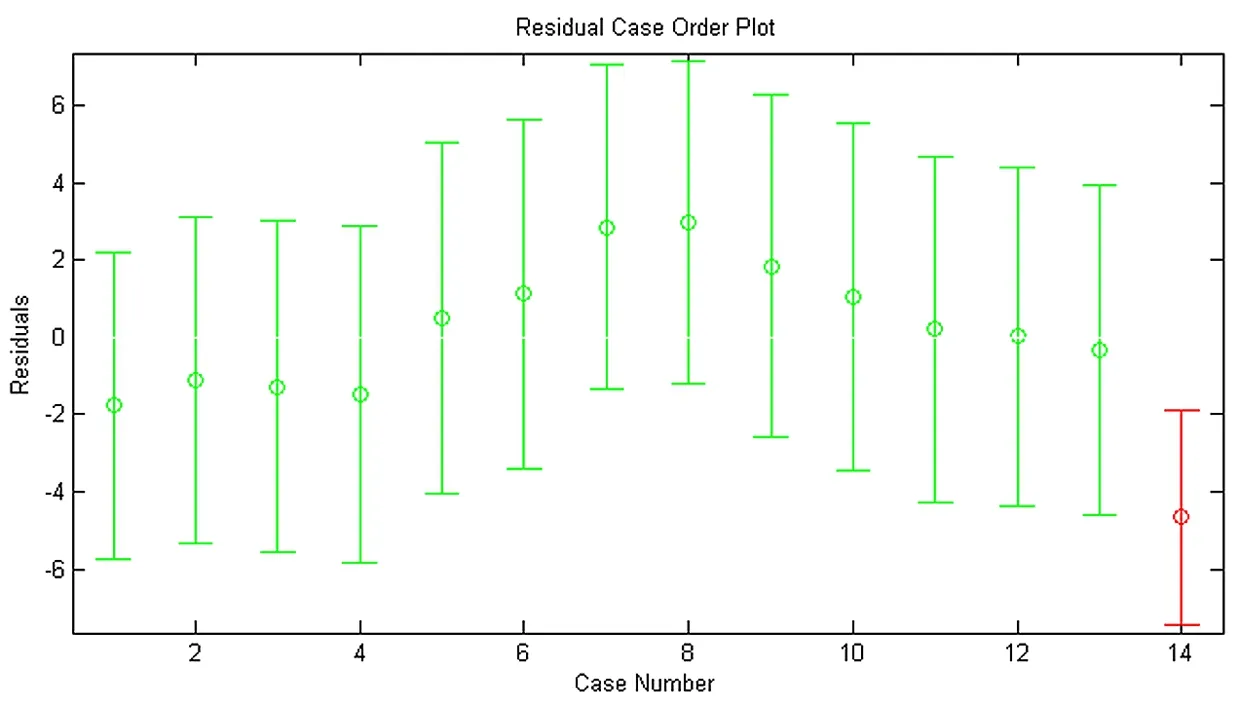
图3 加入粗差数据残差图
通过图3加入粗差数据残差图可以看出,12月1日观测数据是一个明显的粗差。
最小二乘分析的到回归系数b4=-1.329 9,b5=-0.192 5,故最小二乘法得到的一元线性回归方程为:

(11)
同理利用稳健估计回归分析得到一元线性回归方程系数b6=-0.860 6,b7=-0.206 7,故稳健估计法得到的一元线性回归方程为:
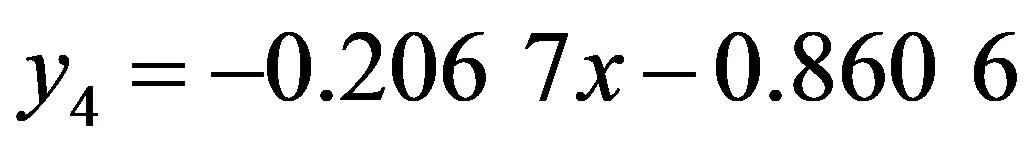
(12)
图4所示为加入粗差后2种不同方法拟合方程图:
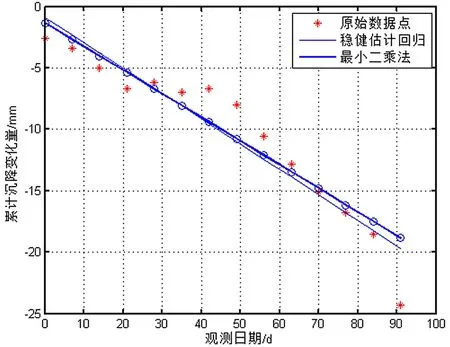
图4 加入粗差后2种不同方法拟合方程图
从图4中可以看出,在60~90 d累计观测时间段稳健估计拟合效果更好,更加接近存在粗差时真实的观测值。通过计算可以得出,在原数据加入粗差的情况下,两者方程差异显著,其中采用最小二乘法和稳健估计法计算的中误差分别为2.020 5、1.898 6,通过中误差数据,可以明显得到,利用稳健估计法得到的中误差要小于利用最小二乘法得到的中误差,利用最小二乘法与稳健估计法计算残差平方和分别为55.760 4、53.073 8,从残差平方和结果可以看出,利用稳健估计法得到的残差平方和要小于最小二乘法得到的残差平方和。通过最小二乘法和稳健估计估计法中误差和残差平方和对比可知,在观测数据中存在粗差的情况下,稳健估计相较于最小二乘拟合效果更好。
4结论
(1)在沉降观测数据没有粗差时,采用最小二乘法和稳健估计法分别对观测数据处理时,2种方法中误差和残差平方和没有明显差异,都可用于沉降观测。
(2)当沉降观测数据存在粗差时,采用最小二乘法在数据处理时,计算结果偏差较大,拟合效果偏离真实值,采用稳健估计法时,其拟合效果以及中误差和残差平方和,均优于最小二乘法估计,能够对存在粗差的观测数据起到抗差的作用。
