磁粉检测中修磨坑底部检测灵敏度问题分析
2021-12-22颜信全侯佳保杜伟
颜信全,侯佳保,杜伟
广州黄船海洋工程有限公司 广东广州 511462
1 序言
磁粉检测是工业上常用的表面无损检测方式之一,裂纹是磁粉检测中最常见的缺陷。工件中最容易产生裂纹的区域,往往是高强钢、大厚度、高应力区域,这些区域也是工件的重要区域,一旦这些区域失效,将会对结构安全带来重大威胁。由于上述区域所采用的通常是特殊钢材,所以多次受热将会影响母材的力学性能;同时,由于裂纹在局部受热时有延伸倾向,所以工业中对于裂纹,通常采用机械打磨的方式进行清除。
由于裂纹是危害性最大的缺陷之一,所以裂纹清除后,需要对工件进行检测,确保没有裂纹后再进行补焊,并在补焊后,满足延时要求再进行复检。对于打磨处的凹槽内部(见图1),检测灵敏度是否满足磁粉检测的要求,则需要进一步讨论。此外,对于厚板焊缝打底焊进行磁粉检测,也有同样的问题,打底焊的磁粉检测可以认为是凹槽很长的特殊情况。本文通过简化模型,基于有限元仿真进行计算,对磁粉检测中修磨坑对灵敏度的影响进行探讨。

图1 裂纹打磨返修产生凹槽
基于有限元的仿真分析法,本文还对磁轭间距对检测区域内磁场的影响进行了讨论,了解磁轭间距变化对磁通密度的影响。对于凹槽处磁场强度的变化,可以通过调整磁轭间距来进行补偿。
2 理论模型
2.1 建立几何模型
现实工件中的返修凹槽往往是不规则的,裂纹的形状也是多种多样。为便于讨论,本文假设凹槽和裂纹为矩形,且裂纹位于方坑底部,如图2所示。
对于大部分裂纹处的修磨坑,凹槽的长度是有限的,不能忽略不计,二维模型主要适用于焊缝打底焊道进行磁粉检测的情况,或者当修磨坑远大于磁轭宽度时,才能适用。不过,在固定凹槽长度的情况下,对二维模型进行定性分析,对于了解凹槽宽度和深度变化对底部裂纹漏磁场的影响,也具有一定的参考价值。
2.2 磁路理论分析
图2a所示的二维模型,可以按照磁路理论[1],对凹槽段的磁路特性进行分析,推导出裂纹的磁通密度B与凹槽尺寸的关系。根据裂纹的磁通密度B与开口处邻近区域漏磁场的关系,可以定性分析漏磁场与凹槽的关系。

对于式(11),Φ为固定量,是由磁轭通磁大小决定的,μ0、μr和T是由给定的材料和板厚决定的,DL为研究区域的长度,DL的长度足够长,使进入研究区域和离开研究区域的磁力线平行于钢板,d、h为检测目标裂纹的宽度和深度,可以根据常见的最小裂纹要求进行设定。此式(11)即为凹槽宽度W、深度H与裂缝磁通量关系的函数,有了凹槽与裂纹磁通量关系,再进一步讨论凹槽与漏磁场的关系。
2.3 绘制函数的曲线
将式(11)对部分变量赋值,可以计算出凹槽宽度W和深度H对气隙处磁通量影响的关系曲线,如图4和图5所示。
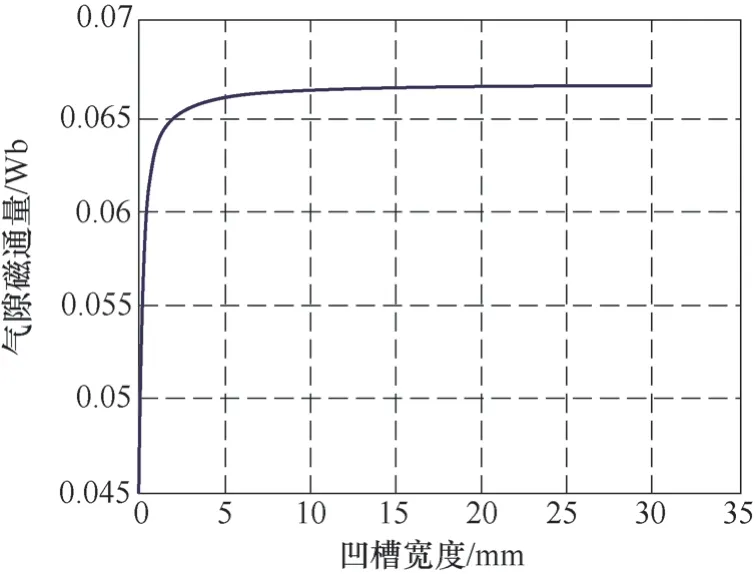
图4 凹槽宽度W对裂纹气隙磁通量的影响
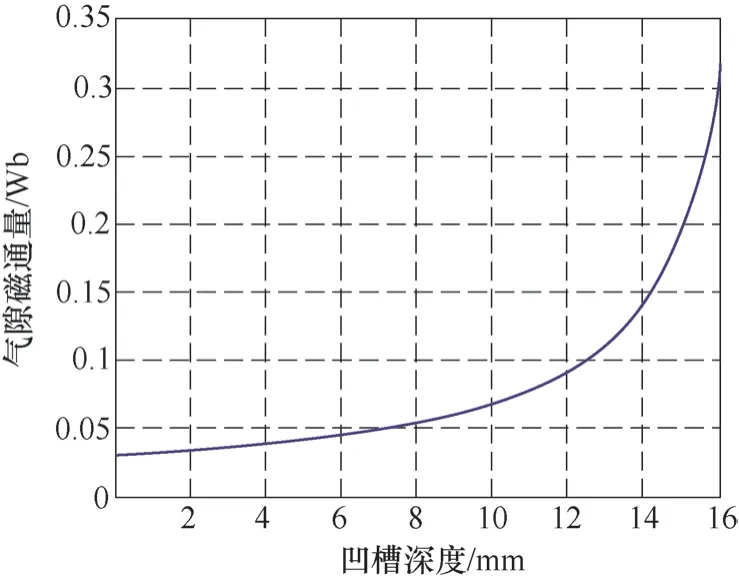
图5 凹槽深度H对裂纹气隙磁通量的影响


2.4 磁通密度B
得出裂缝处的磁通量,不难算出磁场的磁通密度为

根据磁场强度与磁通密度的关系

由于磁粉颗粒的分布难以确定,所以要计算缺口处的磁粉颗粒的磁感应强度是很困难的。本文通过计算缺口处的空气磁感应强度来讨论漏磁场的变化,由于空气的磁导率变化极小,可以当做常量,所以缺口处的漏磁场与空气磁感应强度成正比。
为便于讨论,本文采用裂缝处的空气磁感应强度(磁通密度)B2,来反应漏磁场强度的大小(下同)。
基于有限元的仿真分析发现,离开裂缝的邻近区域的磁场强度随距离快速下降,0.2mm×3mm裂缝在1mm距离内,磁通密度就下降了90%(见图6)。
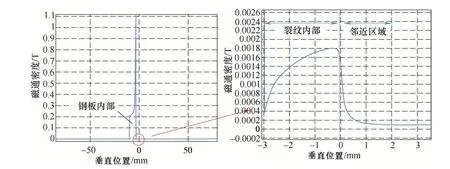
图6 裂缝气隙与钢板中的磁通密度比较
因此,图4和图5所绘制函数的曲线特性,基本上反应了漏磁场强度的变化特性,只是单位和量纲上的差别而已。
2.5 凹槽附加磁场的影响
值得注意的是,凹槽底部的裂纹,由于其开口处的磁通密度B将会受到凹槽本身空间的磁场影响,所以在计算漏磁场时,应考虑将凹槽气隙本身的磁场磁通密度去除。
同样的原理,可以计算凹槽中心的磁通量Φ1和磁通密度B1
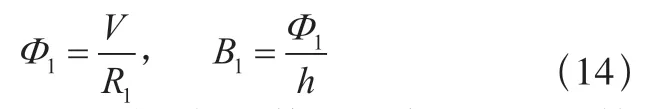
所以,与凹槽处磁粉检测的灵敏度相关量,是

图7和图8绘制了凹槽尺寸与ΔB的关系曲线。
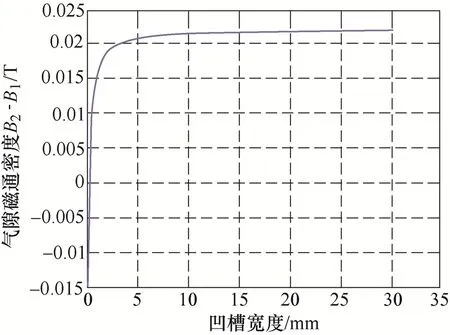
图7 凹槽宽度对裂纹气隙磁通密度B的影响
由图7和图8可以看出,B2-B1的曲线特性与气隙磁通量曲线特性并没有发生变化,说明在理想模型下,凹槽空间的磁通密度很小,并没有对裂纹的漏磁场产生影响(实际情况下是有影响的,三维情况下的仿真计算将在下文讨论)。
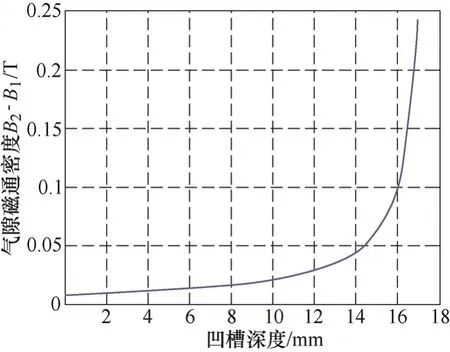
图8 凹槽深度对裂纹气隙磁通量密度B的影响
对于三维模型,在凹槽和裂纹的两端增加完好钢板的磁通区域,并加入凹槽和裂缝的长度进行计算,同样可以通过进行串联和并联的磁阻运算,可以得出漏磁通与凹槽参数之间的关系。但是,由于钢板的宽度远远大于讨论区域的宽度,故将钢板其他区域并联进入磁路,将会使磁阻趋向于0,计算结果误差将会很大。在三维模型的裂纹漏磁场与凹槽尺寸的关系,可以采用有限元分析法来进一步讨论。
3 有限元分析法
3.1 实际工件与理论模型的差距
前面的理论模型是基于凹槽两端的磁通量均匀,研究区域两端的磁导率趋向无穷大的情况下讨论的。实际情况下,钢板的磁导率虽然很大,但并不能当无穷大来处理,实际上图6也说明了钢板内部以及裂缝气隙内的磁通密度是不均匀的,否则,磁通密度曲线应该是平直的矩形状。
图9显示了在三维仿真条件下,凹槽和缝隙的磁通密度B分布情况。由此可以看到,由于空气缝隙的挤压,钢板上部靠近凹槽的区域磁通密度比较小,钢板下部磁通密度比较大。漏磁场与凹槽尺寸的关系是一个复杂的微积分函数,解决复杂微积分问题比较简单的方法是采用有限元分析法,将研究的问题分成许多个域,把复杂的问题分解成许多简单的问题的集合,如图10所示。
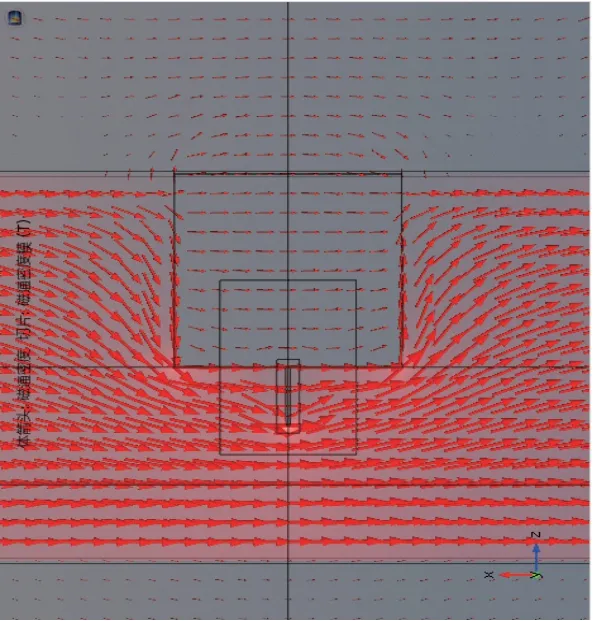
图9 磁通量密度分布(模拟)
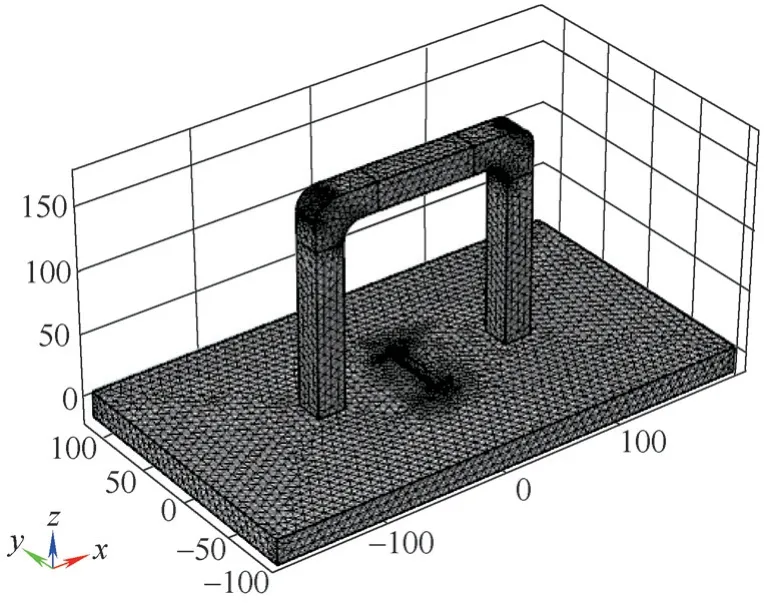
图10 有限元网格划分
3.2 有限元分析法
有限元分析(FEA,Finite Element Analysis)利用数学近似的方法对真实物理系统进行模拟。还利用简单而又相互作用的元素,即单元,就可以用有限数量的未知量去逼近无限未知量的真实系统。
有限元分析是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。这个解不是准确解,而是近似解,因为实际问题被较简单的问题所代替。由于大多数实际问题难以得到准确解,而有限元不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。
本文采用Comsol有限元分析软件,基于磁通量守恒原理,在有限的域内计算磁通量密度的分布,得出漏磁场与凹槽尺寸之间的关系。
本文根据船舶行业中,常见的裂纹尺寸,选择宽度d=0.2mm,深度h=3mm,长度与凹槽长度一致的裂缝作为参考检测标的,计算漏磁场与凹槽尺寸之间的关系。计算所采用的钢板相对磁导率为700,见表1。
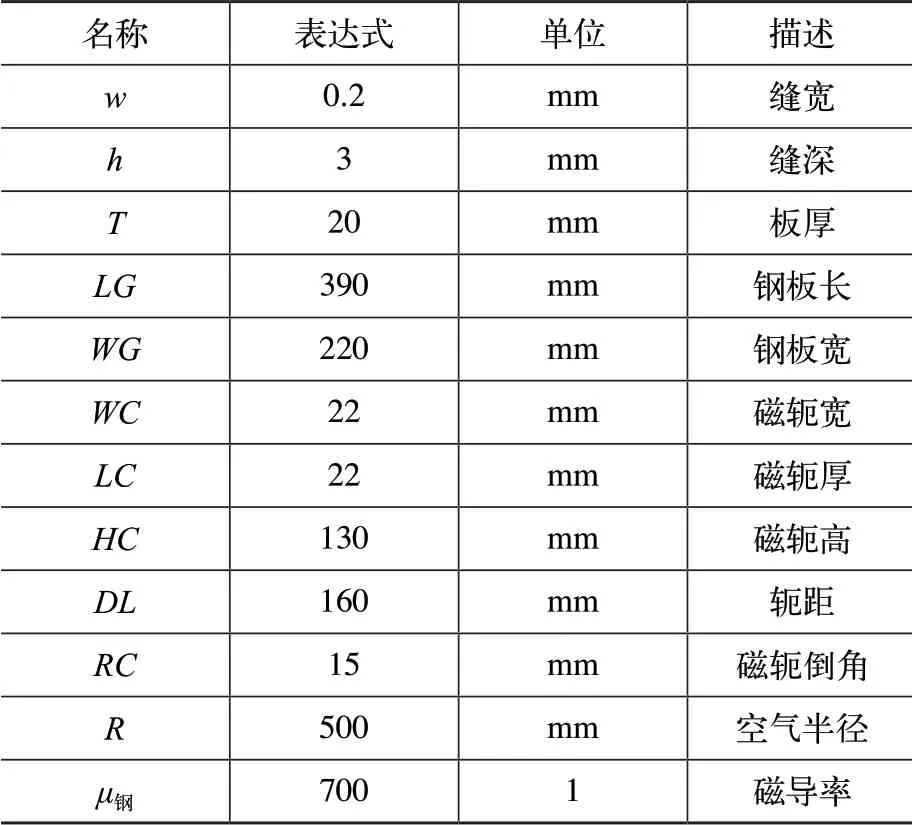
表1 仿真参数
3.3 凹槽宽度对漏磁场的影响
图11所示为根据表1参数计算的修磨坑宽度与裂纹气隙磁通密度之间的关系。
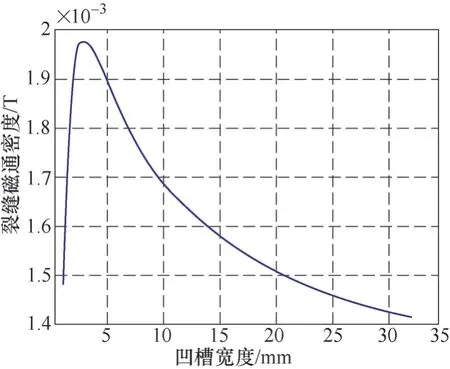
图11 修磨坑宽度与裂纹漏磁场的关系
如图11所示,凹槽宽度增加时,对漏磁场先是快速上升,在宽度达到2.5mm左右时,漏磁场开始下降,这个结果与图7的二维模型计算结果有所不同,为了直观地比较两个研究模型的差值,将两个曲线归一化后,进行比较。
如图12所示,红色实线为按照二维模型计算的凹槽宽度与裂纹漏磁场关系曲线,蓝色点间线为在三维模型中,采用有限元分析法计算的凹槽与裂纹漏磁场的关系曲线。由此可看出,二维模型计算结果与三维有限元分析结果存在凹槽宽度比较小时比较吻合,当凹槽宽度比较大时,两个曲线开始分离,凹槽尺寸与裂纹磁场的关系可以分为两个阶段。
女儿在法国上中学和小学,每门课都很出色。对于成绩好的学生,学校的老师都希望上大学时选择理科。女儿却偏偏选了文科,并且还选了最冷门的图书专业。老师要我试着说服女儿攻读理科,并且还要推荐她进名牌高校。当我向她提及老师所说的,将来文科的出路恐怕不乐观之时,女儿却反问我,你不是常常告诉我们:“要以读书为乐,不要为了功利吗?”
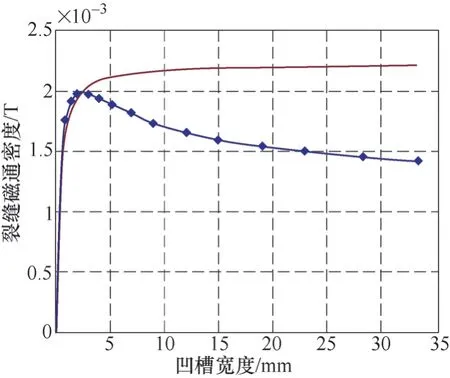
图12 二维和三维模型中的宽度关系曲线比较
第一个阶段:在凹槽宽度增加的起始阶段,凹槽尺寸与裂纹尺寸相近,凹槽底部裂纹的漏磁场随着凹槽宽度增大而快速增加,其主要原因是凹槽处的磁阻快速增大,磁力线向裂纹和下部钢板挤压。在这个阶段里面,部分通过裂纹的磁力线,也会受到凹槽两端邻近的钢板影响,对裂纹开口处的磁场强度有加强作用,如图13所示。
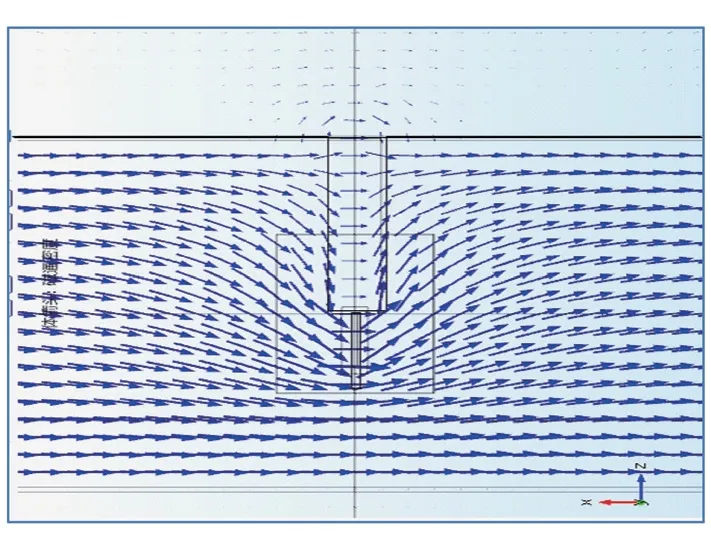
图13 凹槽附近钢铁对裂缝磁场的增强作用
第二阶段:当凹槽宽度增加,远大于裂纹尺寸(0.2mm)时,凹槽处磁阻增加对于磁力线的挤压作用逐渐变小,同时凹槽壁旁边的钢板距离变大,对裂纹区域的加强作用快速消失。当加强作用的减少值大于挤压作用的增加值时,裂纹处的漏磁场开始逐渐变小。当凹槽宽度很大时,增强作用趋于0,裂纹处的漏磁场趋向于稳定值(见图14)。
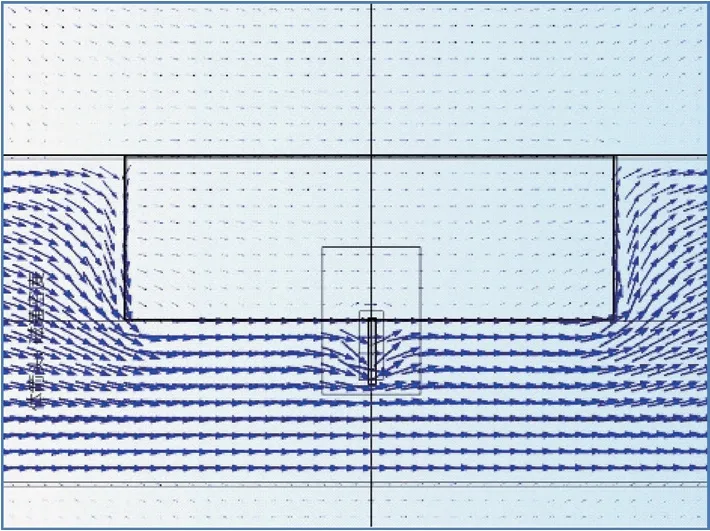
图14 当凹槽很宽时的磁场分布
因此,两个曲线的区别在于二维模型将研究区域简单的划分成互不相干的三层介质(见图15),把磁力线当成是全部平行于钢板平面来研究,但是在实际介质中,邻近介质层的变化,会对磁力线的分布产生影响,实际磁力线不是完全平行分布的。

图15 二维模型中的理想介质分层
3.4 凹槽深度对漏磁场的影响
图16所示为根据表1参数计算的修磨坑深度与裂纹气隙磁通密度之间的关系。
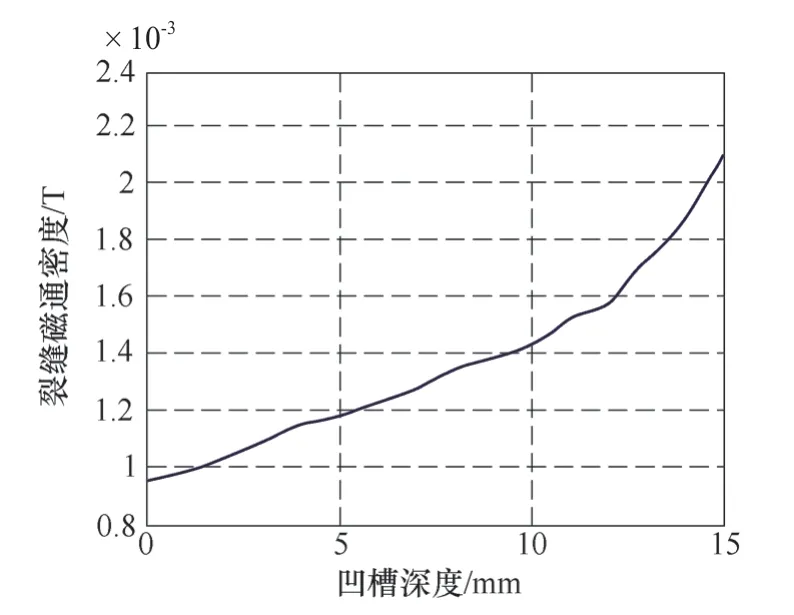
图16 凹槽深度对裂纹漏磁场的影响
由图16可以看出,修磨坑的深度越大,底部裂纹的漏磁场强度越大。这是因为深度加大造成凹槽磁阻的增加,磁力线向裂纹和下部钢板挤压造成的,结论与二维模型计算结果(见图8)一致。
通过归一化处理将两图放在一起比较,如图17所示。
从图17可以看出,三维有限元模拟结果中,裂纹处的磁通密度随深度的变化速率要小于二维模型计算结果,这主要是因为在三维模拟中,凹槽的长度是有限的,当凹槽深度增加时,部分磁力线被挤压后,通过凹槽两端的钢板绕过凹槽回到磁轭中。因此,即使不考虑磁饱和的问题,也不会出现图8中,凹槽和裂纹深度之和接近板厚时,裂纹磁通量密度快速上升的情况。
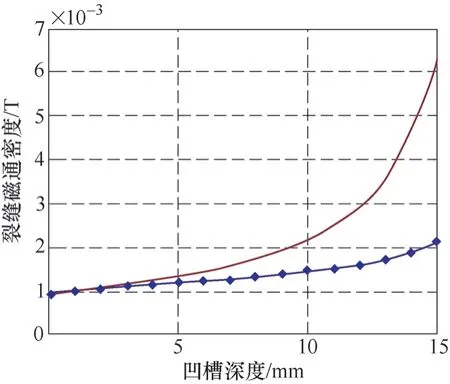
图17 二维和三维模型中的深度关系曲线比较
3.5 凹槽长度对漏磁场的影响
图18为凹槽长度与底部裂纹漏磁场的关系曲线,不难看出,当凹槽长度增加时,凹槽的所占据的面积增大,由于凹槽的空气磁导率低于原有钢板的磁导率,所以造成裂纹上方磁阻增大,磁力线向裂纹和下层钢板挤压,裂纹漏磁场增大。当凹槽趋向无限长时,裂纹出的漏磁场趋向稳定值。
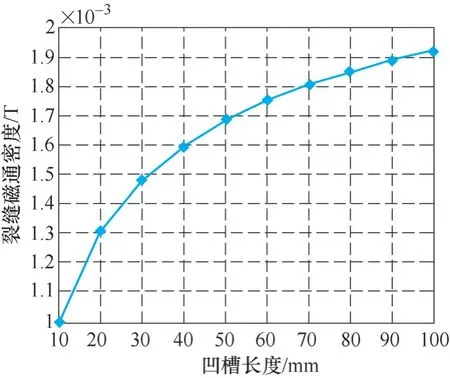
图18 凹槽长度与底部裂纹漏磁场的关系
3.6 磁轭间距对磁场强度的影响
图19为磁轭间距与底部裂纹漏磁场的关系曲线。由此可以看出,裂缝处的漏磁场随着磁轭间距的增大而逐渐减小,这是因为随着磁轭间距的增大,磁力线的发散面积变大,凹槽处所占的总磁通量变小的缘故。
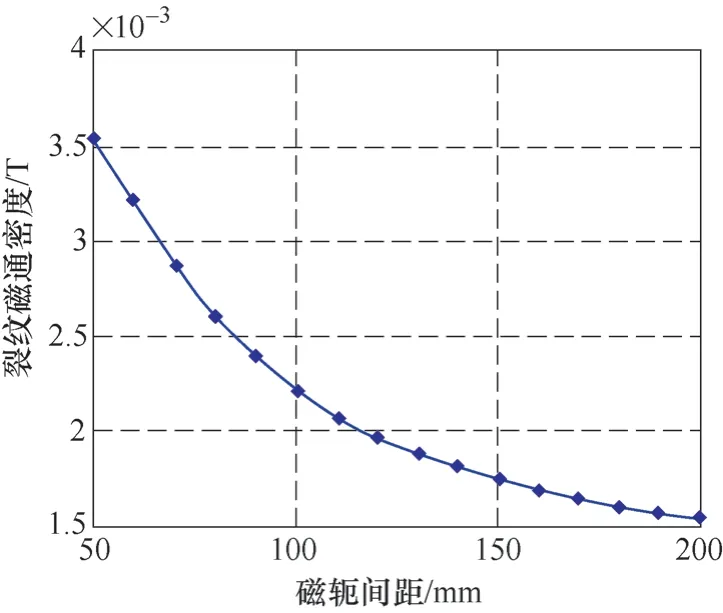
图19 磁轭间距与底部裂纹漏磁场的关系曲线
4 实际检测中的其他因素
4.1 磁导率的变化的影响
由于磁场强度的变化,磁导率也会发生变化,尤其是当材料达到磁饱和状态时,裂缝下部的钢板磁场强度不再增加,所以磁力线将会有向裂缝挤压的倾向。由此可见,在磁场强度很大时,实际的漏磁场强度要比本文2、3部分讨论的情况更大一些。
4.2 趋肤效应的影响
对于交流电磁轭所使用的交流磁场,当凹槽比较浅时,由于趋肤效应的影响,实际的表面漏磁场比直流的情况要大,所以当凹槽很深时,漏磁场比直流的情况要小。
5 结束语
本文基于磁通路磁阻理论结合有限元仿真分析,讨论了磁粉检测中,修磨坑对漏磁场的影响。
1)当打磨宽度很小时,底部裂纹漏磁场随着修磨坑宽度增大而增大,当修磨坑宽度远大于目标裂纹时,底部裂纹漏磁场随着修磨坑宽度增大而逐渐减小,并趋向一个稳定值。
2)修磨坑深度增加时,底部裂纹漏磁场随着打磨深度增大而增大,由于磁饱和的限制,最终趋向一个稳定值。
3)当修磨坑长度增大时,底部裂纹漏磁场随着修磨坑长度增大而增大,并逐渐趋向稳定值。
4)当磁轭间距增大时,修磨坑底部裂纹漏磁场随着磁轭间距增大而减小。
