2011年泰州中考数学第28题解析

张美娟 焦建林

(江苏省泰兴市洋思中学 225400)

一、原题呈现

2011年泰州中考第28题：在平面直角坐标系xOy中，边长为a(a为大于0的常数)的正方形ABCD的对角线AC、BD相交于点P，顶点A在x轴正半轴上运动，顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O)，顶点C、D都在第一象限.

(1)当∠BAO=45°时，求点P的坐标；

(2)求证：无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动，点P都在∠AOB的平分线上；

(3)设点P到x轴的距离为h，试确定h的取值范围，并说明理由.

二、试题分析

这试题来源于苏科版教材八年级(下)第95页的第22题：如图，正方形ABCD的对角线AC、BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合，将正方形A′B′C′D′绕点A′旋转，在这个过程中，这两个正方形的重叠部分的面积会发生变化吗？

该试题保留了原来的正方形ABCD，并把正方形ABCD放置到平面直角坐标系中，然后让正方形ABCD的顶点A和顶点B分别在坐标轴上运动，保持边长不变．

重点考查点的坐标、勾股定理、全等三角形、三角形的中位线、角平分线定理的逆定理、等弧所对的圆心角相等、不等式组、三角函数等知识点．

这种命题方式是从教材出发，充分挖掘教材的命题价值，一方面关注了学生的应试心理，另一方面，引导教师教学要追本溯源，发挥教材的教学价值．

三、解法探索

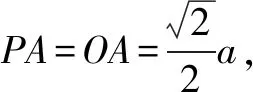
(2)本小题我们可以从多个角度、用多种方法解决．

方法1要证明点P在∠AOB的平分线上，其实就是要说明点P到∠AOB的两边距离相等，因此就可以考虑经过点P分别作OA、OB的垂线段，垂足分别为点F、点E，如图2.因为∠AOB=90°，∠EPF=90°.由(1)可知，∠BPA=90°，所以∠EPB=∠FPA.由(1)可知，PB=PA，所以△EPB≌△FPA(AAS)，所以PE=PF，即点P到∠AOB的两边距离相等.所以无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动，点P都在∠AOB的平分线上.

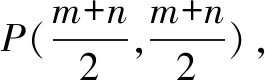
方法3要证明点P在∠AOB的平分线上，其实就是要说明点∠AOP(或∠BOP)=45°，那原来图形中有

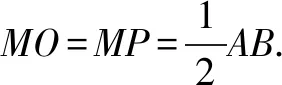
(3)过点P作PG⊥x轴于点G，因为点P到x轴的距离为h，所以PG=h.

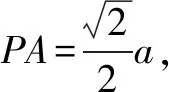
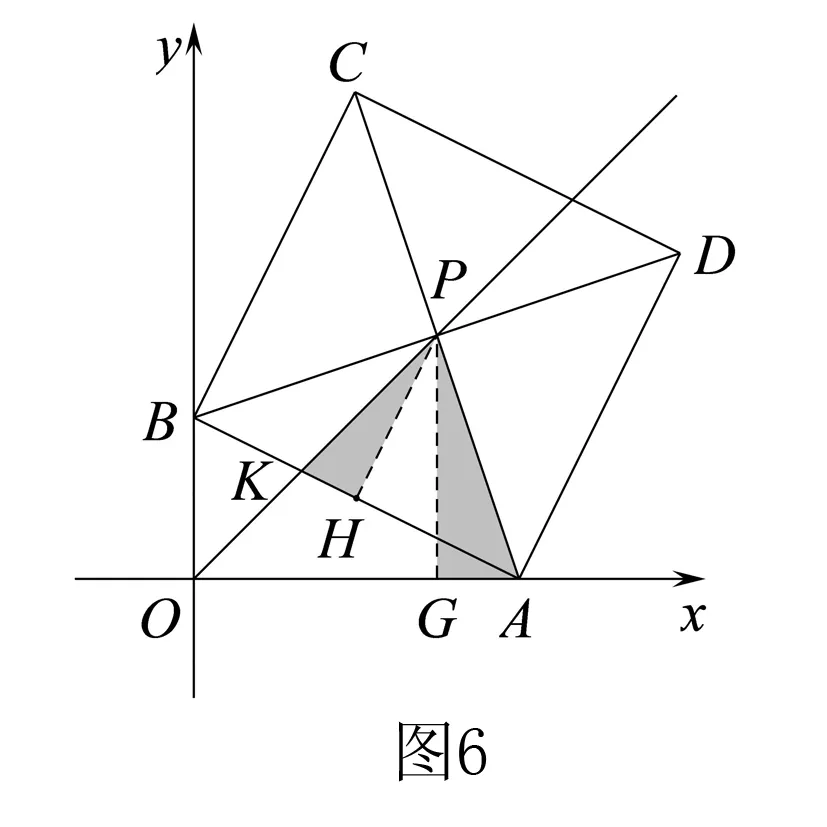
好的中考试题不仅考查数学知识和数学素养，还应该具有充分的发展性，让学生有回味无穷的感觉．

总之，本题的本质就是 “由特殊及一般”，通过减少或弱化条件实行一般化，利用数形结合由数量关系和图形关数形结合，以及对现象提出质疑、猜想结论并验证结论，建构模型解决问题等等都是创新的方法，这些方法是联结数学知识与迁移创新之间的桥梁.