对分层、分组、合作教学模式的研究

陈玉兰

(江苏省如皋初级中学 226500)

随着新课改的推进，分层、分组与合作学习的教学模式，越来越受广大教育工作者的重视.这种教学模式是在“因材施教”理念的贯彻下，将认知水平、实践能力及情感意志等方面有所差异的学生进行整合，开展合作学习，获得发展.将分层与合作融合于一体，可使得学生的差异性资源在教学中有效释放，最大限度提高学生的积极性，使得每个学生都获得不同程度的成长.

一、理论基础

1.现代教学理论

现代教学理论提出：将个别引导、分组合作与班级集体授课等教学方式结合在一起，能有效地提高教学成效.这与巴班斯基所提出的“教学形式最优化”的理念不谋而合.学生在综合化的教学模式下张扬个性、各挥所长、促进发展.

2.掌握学习理论

教育家布卢姆在他的掌握学习理论中提出：“学生虽存在个体差异性，但通过学习，每个人都有能力理解所学内容，达到预期的教学水平；他着重强调：教师应尽可能地为学生提供好的学习环境，学生在良好的学习条件下，存在学习速度、动机与能力等方面的个体差异性会逐渐缩小，乃至消失.”

3.合作学习理论

教育书籍《学记》中载有：“独学而无友，则孤陋而寡闻.”一个孤立的学习者犹如井底之蛙，总以为自己能看透一切，其实仅仅局限于自我狭小的范围内.这就要求我们学生在学习中要融入群体，与同伴取长补短、互相切磋，则能获得共同成长.

二、方法与步骤

1.调研学生水平，合理分层分组

分层，并非纯粹地依靠学习成绩来划分，还要关注学生的心理状态、情感倾向以及协调能力等诸多方面的因素.只有对学生进行了客观、公平、公正的分析与研究后，才能做到真正意义上的合理分层.一般我们根据学生的综合水平，将他们分为三层：A.基础层；B.普通层；C.提高层.一旦分层确定，就可以着手分组工作了.

分组，是在分层的基础上，遵循“组间同质，组内异质”的原则，将不同能力水平的学生组合到一个小组内.例如班上有40名学生，教师可根据学生分层情况，以1∶2∶1的模式进行分组，共分成10个小组.此过程中尤其要注意非智力性因素的影响，除了成绩之外，要重点关注学生的人格、适应能力以及心理状态等，分组的目的就在于促进每个学生的发展.

分层、分组确定之后，就进入分工阶段.每个成员都有自己独特的个性，分工时要考虑学生的特长，让每个学生都要有自己的有角色担当，尽可能将自己的能力发挥到极致.如小组四人，可设立组长、记录、资料员与汇报员.

(1)组长：选择合作意识与组织能力强，在学生中有一定威望的学生来担任.主要负责协调组内整体工作，如组内成员的操作、探究或交流等，不可让合作偏离轨道.组长最重要的职责是保证小组活动能有序开展，并让每个学生在活动中都能积极参与，在动手、动脑中开启思维、拓展思路、共同进步.

(2)记录员：选择写字清晰且速度快，并有较强责任心的学生担任.主要负责记录组内合作交流的过程、疑问、解决办法、相关决议以及讨论结果等.

(3)资料收集员：选择知识面广的“百事通”担任此职责.主要负责各项资料的搜集与整理，为问题的解决做好保障.

(4)汇报员：选择有较强的语言组织能力与表达能力的学生担任.主要负责将记录员整理的资料汇总、清晰表达.

2.改变教学结构，合作共同提高

新课标明确提出学生是课堂的主人，如今新课改的大力实施也明确了学生的主体性地位.如今的数学课堂一改传统的“注入式”模式，而是在教师的引导下，学生主宰着自己的学习.合作学习是“以生为本”的具体体现，学生根据教师提出的探究主题，自主分析、交流、思考、推理和总结，用集体的智慧完成一个共同的教学任务.

案例：“三角形中位线定理”的教学

课堂伊始，教师以趣导入，让学生对三角形中位线的基本概念产生初步认识.在此基础上，开展如下教学活动：

(1)自主操作

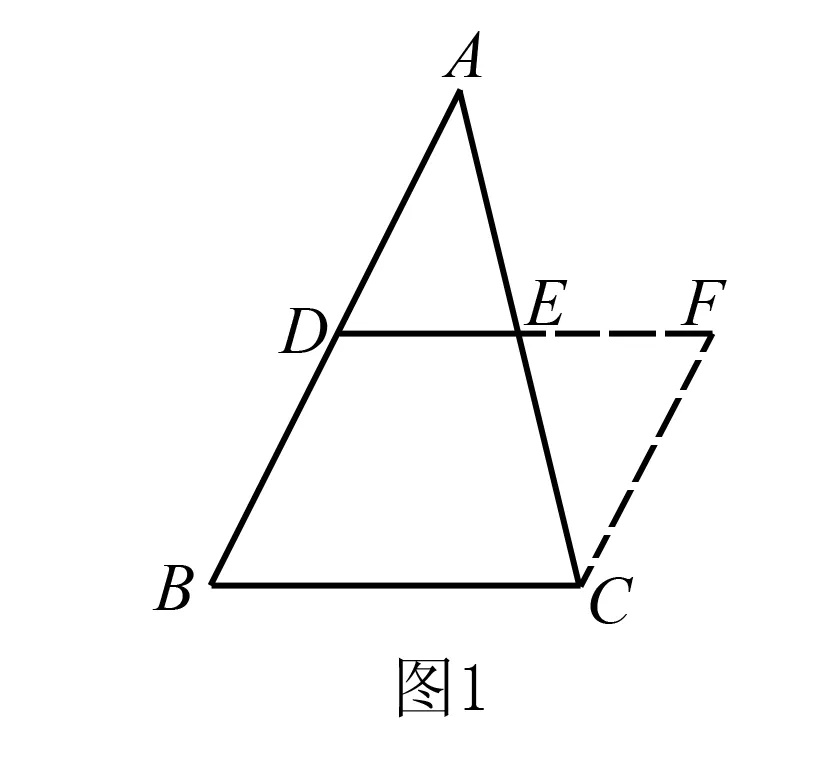
学生取出预先准备好的三角形纸张，如图1，沿着中位线DE剪开，将△ADE拼接到梯形DECB上，获得一个四边形BDFC.观察所获得的图形，大部分学生猜想：这是一个平行四边形.此时教师提出：“请大家合作交流，讨论一下拼接而成的图形为平行四边的证明过程.”

学生通过剪与拼的过程，一眼就看出中位线与原三角形的底边呈现出平行的关系，至于如何证明，仍需进一步研究.

(2)合作交流

学生在动手操作的基础上，进行合作交流，思路则清晰了很多.各组积极讨论，获得以下证明方法：

如图1，DE为△ABC的中位线，因为△DEA≅△FEC，所以可知DA=FC，∠EDA=∠F，由此可知DB‖FC.由AD=DB可得BD=FC，由此可确定拼接而成的四边形为平行四边形.

师：通过以上证明过程，我们能确定DE与BC的位置与数量关系吗？

生1:刚刚已经明确证明四边形BCFD为平行四边形，那么DE‖BC，至于数量关系，还得研究下.

师：现在请各组再次讨论，证明DE与BC具有怎样的位置与数量关系.

(学生合作学习)，各自展示答案.

学生通过自主证明，对中位线的定理有了明确的认识.不论那种方法，关键点是作准辅助线，不论是延长还是取长补短，都需要在学生思考的基础上，教师给予引导与点拨，如此可让学生充分体验探究的乐趣，对学习充满信心.

3.及时分层练习，评价总结提高

练习能深化学生对知识的理解、巩固与运用.根据学生实际情况，教师在设计练习时要注意分层，让每个学生都能在练习训练中获得学习带来的愉悦感，增强信心.

练习设计：

(1)如图2，已知一个三角形支架ABC的周长是90cm，求该支架三条中位线组成的三角形周长为多少？

(2)如图3，池塘的宽度为BC，一位工人在平地上选了一点点A，又分别找到AB与AC的中点点D与点E，若测得DE=18，求该池塘的宽度BC.

几道练习都是围绕本节课教学重点而展开，但难易程度却有所区别.对于不同层次水平的学生，教师可提出不同的完成要求.同时也鼓励低层次水平的学生探索高层次的练习，在“跳一跳，摘到桃”中获得成长.

总之，分层、分组、合作教学模式，将传统课堂转变为“以生为本”的现代化数学课堂，学生在小组合作中抱团前进，不仅获得知识与技能，更重要的是拓展了思维，并形成了良好的合作与学习能力，提升了数学核心素养.