整合课程资源 创新数学教学

赖巧云

(福建省龙岩市第五中学 364000)

课程资源的整合，与培养学生的综合能力是一致的，教师要积极拓展课程资源整合范围，创新数学教学方法，让学生从数学知识、技能、思想、经验积累中，获得全面发展.

一、突破学科屏障，启迪学生对数学的深层思维

在课程整合背景下，对数学教师而言，既要关注数学知识的有效整合，还要能够突破学科壁垒，关注数学与语文等其他学科间的融合.

1.以《西游记》人物顺序来诠释数学课程结构特点

在数学教学中，往往教完一节进行课程复习时，学生对已学知识存在忘记的现象.对课程进行有效复习与回顾，有没有良好的方法，能够让学生快速、准确、高效地记住本章知识点？在学习“数轴”一节时，我们借助于《西游记》中的人物出场顺序，将数学中的有理数、无理数，以及数轴、绝对值、相反数等进行有效串联.对于有理数、无理数的辨析，我们已经学习，并初步掌握如何分辨的方法.但面对教材中知识点的逻辑顺序，很多学生搞不清前后.在看《西游记》时，对于孙悟空及师徒四人的出场顺序，请同学回忆一下，谁最先出场？接着是谁，后来是谁？《西游记》里的人物众多，有仙、有人、有妖.但对于出场顺序，总要按照故事情节的发展逐一出场.同样，对照故事人物的出场顺序，我们在学习过有理数，再掌握无理数后，展开了数轴学习，认识数轴的特点与数的对应关系，之后，还要延伸绝对值、相反数等知识点，使其成为贯通的整体.如此以来，数学知识点不再是孤立的，而是可以整合在一起的.学生不仅做到“知其然”，更能够知其“所以然”，增进对数学课程结构的深度理解.

2.以《三国演义》人物描写来诠释数学数形结合思想

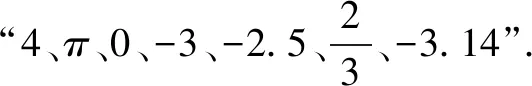
3.以《水浒传》故事情节来展现数学解题思维

在数学中，解题是重要部分.但对于学生，因缺失数学思维，导致找不准解题思路.怎样让学生走出解题的“死胡同”？以“绝对值”教学为例，对于某数轴上的A、B两点，其两点距离可以表示为|a-b|.如下图所示.

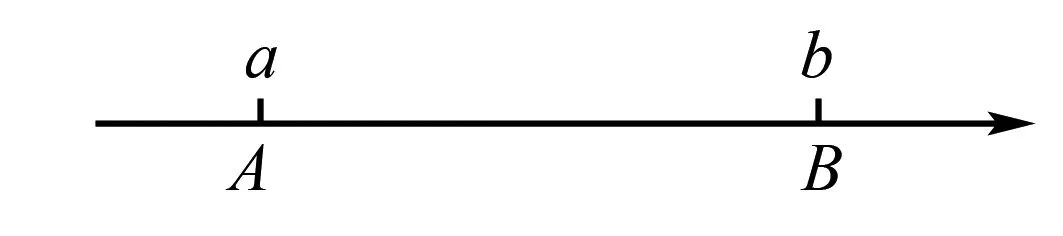
根据该题回答如下问题：对于数轴上表示“3”与“-2”的两点距离是多少？求代数式|x-1|+|x-2|+|x-3|+…+|x-2014|+|x-2015|的最小值？对于第一问，我们根据数轴，将对应的数代入|a-b|中，很快就得出答案.但对于第二问，很多学生感到困惑，不知如何下手，更无法找准解题思路.为此，我们引出《水浒传》中“三打祝家庄”故事.对于宋江所带领的队伍，在第一次攻打祝家庄时，失败了，第二次进攻，又失败了.之后，宋江与各位将领分析失败原因，对敌情不了解，攻打方法不当.在第三次攻打之前，先摸清盘陀路，后拆散李家庄、扈家庄、祝家庄的战略联盟，然后在敌人营盘布置伏兵，最终取得胜利.可见，面对复杂问题时，我们要向“三打祝家庄”学习，先找到关键点，再展开求解探究.我们可以先对|x-1|+|x-2|+|x-3|进行讨论，再由此总结解题规律，从而找到从“特殊”到“一般”的解题思路.

二、整合生活资源，夯实学生对数学的深刻认知

数学源于生活，在数学创新教学中，教师可以充分整合生活化资源，来延伸数学实例，激发学生兴趣，促进学生对数学知识的理解和把握.

1.从生活中运用数学方法解决实际问题

数学知识在讲解和运用中，具有一定抽象性，学生理解上有些难度.数学本身与生活实例的结合，可以丰富学生对数学情境的感知，增进对数学的学习积极性，还能够运用数学知识解决生活实际问题，提高学生的数学思维力.在学习“数据的集中趋势”时，我们对于数据的收集、整理方法，直接以班级学生某组的单元测试成绩进行比较，让学生从“97、92、95、99、87、100、74、62、83、91”等成绩中，去计算本组数据的平均数、中位数、众数.根据计算结果来分析，对于平均数，易受到极端值的影响，如本组平均数为88，与“62”这个数值有直接关系.因此，在比赛中，对选手成绩的计算，往往会选择去掉最高分、最低分，之后再求所有成绩的平均值.通过对该组数值进行排序，得到中位数92.4.一般对于数据个数为偶数时，计算中位数时，需要取中间两个数的平均值.对于该组数值，众数是93.由此，对于统计知识的数学方法，学生可以在实例体验中复习旧知，巩固新知，真正掌握解决数学问题的方法.

2.借助生活问题实现感性认知向理性思考的转变

在数学教学中，数学认知力是渐进发展的过程.面对实现问题，教师可以将之转换为生活化现象，让学生去直观地认知，为深刻领会数学本质奠定基础.在学习“一元一次方程”时，该节知识点的呈现，我们可以以生活中手机资费套餐为例，让学生进行感知和体会.在套餐一中，月租为20元，通话计费0.1元/分钟；套餐二中，无月租，但通话计费为0.2元/分钟.请同学们对比分析，哪种套餐资费比较合算？手机资费套餐是学生非常熟悉的生活化问题，借助于该题型的分析，让学生从中认识未知数、方程，从而比较出何种资费最实惠.我们假设通话时间为x分钟，两种资费相同，即得出方程20+0.1x=0.2x，解之得到x=200.也就是说，当通话时间为200分钟时，两种套餐的资费是一样的.但根据这个数值，当通话时间小于200分钟，即x<200，套餐二最实惠；当通话时间大于200分钟，即x>200，套餐一最实惠.这样以来，学生将方程问题与生活问题建立关联，从而强化数学问题的理性思考.

3.借助典型问题整合数学资源

在数学学习中，教师在教学设计上，要关注学生的已有经验，做到因势利导，因材施教.数学逻辑思维的发展，可以结合学生已有经验，引入典型数学问题，开阔学生的解题视野.在学习“二元一次方程”时，前面我们已经了解一元一次方程的知识，我们可以引入学生熟悉的“鸡兔同笼”问题，来构造数学情境.在一元一次方程学习后，我们可以假设鸡的头数，来推出兔的只数，再根据等量关系列出方程.在学习二元一次方程时，我们可以分别假设鸡、兔的只数，然后根据等量关系列出方程组，进而通过解方程组的方式来求解答案.由此，同样的问题，运用不同的解题思路来求解，让学生从中感知问题的求解方法.同样，在数学知识结构中，数学知识点本身并非单一，而是存在相互关联.在数学课堂上，教师可以激发学生自主探究，深化对数学抽象知识的理解，促进数学资源的整合.在学习“图形的相似”时，我们可以围绕“相似”与“全等”的关系，比较两个数学符号的差异性.对于全等符号，表示为“≌”，该符号中包含“∽”与“=”；对于相似，其符号表示为“∽”.可见，全等是特殊的相似，各对应边的比值为“1”.

总之，资源整合的目标在于增进学生对数学知识的理解和应用，帮助学生建构完整的数学知识体系.教师要重视课程资源整合，积极探索资源整合途径和方法，让学生全面认识数学、理解数学，运用数学来解决问题，促进学生数学核心素养的提升.