基于动态贝叶斯网络的接触网系统可靠性研究

焦志秀，于龙

(西南交通大学电气工程学院，四川成都 611756)

接触网露天架设于铁路沿线上空，把从牵引变电所中获取的电能通过与电力机车上部的受电弓滑动接触传递给电力机车[1]，在牵引供电系统中的地位十分重要。然而，由于接触网系统无备用、工作环境恶劣，这种苛刻的运行条件使得其故障常年居高不下[2]。接触网可靠性差已成为影响列车安全、畅通运输的重要因素，这在一定程度上制约了我国铁路的发展。因此，开展接触网系统的可靠性研究具有十分重要的意义。在对接触网系统的可靠性进行研究时通常采用的方法主要有：贝叶斯网络法(Bayesian Network, BN)[3-4]、故障树分析法(Fault Tree Analysis,FTA)[5-6]、马尔可夫分析法[7-8]。采用FTA 和BN 对复杂系统进行可靠性建模与分析时，往往针对的是系统的静态结构，难以反映系统可靠性随时间的动态变化过程。此外，它们无法描述系统的可维修性。马尔可夫分析法虽然能够反映可维修系统可靠性水平随时间的动态变化特征，但在可靠性建模过程中状态空间的数目会随系统规模的增加而呈指数增长[9]，这无形中给模型的建立和求解过程带来了很大的困难。近几年发展起来的动态贝叶斯网络(Dynamic Bayesian Network)技术是建立在静态BN 和隐马尔可夫模型基础上的一类概率图模型，它继承了BN的所有优点，是原始BN 在时间属性上的延拓，非常适合对带有时效特征的可修复系统进行可靠性建模[10-12]。通过引入时间维度，根据基本元件在初始时刻的条件概率和相邻时间片间的状态转移概率，即可建立复杂系统的动态可靠性模型，实现系统整体可靠性水平的动态估计。目前，鲜有论文对接触网系统可靠性及可用性随时间的变化特征进行研究。本文首次将DBN 理论应用于接触网系统的可靠性建模中，综合考虑接触网系统的动态特性和可维修性，通过构建接触网的FTA 模型，利用FTA 向DBN 的转化规则得到接触网系统的DBN 模型，完成DBN 的结构学习和参数学习。然后利用DBN 的双向推理功能求解接触网系统的可靠性模型，通过正向推理对接触网系统在未来某个时刻的可靠度和可用度进行估计，找到接触网系统可靠度及可用度随时间的动态变化规律；通过反向推理实现对接触网系统的故障诊断，用以识别接触网系统的薄弱环节。研究结果能够为接触网系统的检修和维护提供依据。

1 DBN简介与可靠性建模

1.1 DBN简介

BN 通常由有向无环图和条件概率表组成。有向无环图中的每个节点都代表一个随机变量，而节点间的有向线段则表示不同变量之间的依赖关系。各个节点都附有与之相对应的条件概率表，用以表示父、子节点之间的概率依赖程度。在已知网络结构和概率参数的情况下，利用联合概率分布公式可以推理出相关节点在一定状态下的概率值。

将BN在时间维度上进行扩展，即可得到DBN模型。DBN 是由若干个时间片构成的，每个时间片都可将其视为一个静态BN。在建立DBN模型时通常需要满足2个假设：一阶马尔可夫假设和平稳性假设[13]。基于上述2 个假设的DBN 可以定义为：(G0,G→)。其中G0是初始网络，G→是转移网络。初始网络由一个静态BN 构成，指定了初始时刻的网络结构及概率分布P(X0)。转移网络是一个包含了2 个时间片段的BN，指定了两相邻时间片间的网络结构及概率分布P(Xt|Xt-1)。利用初始网络和转移网络的条件概率分布便可延展DBN 的结构至任意T个时间片，与之对应的各节点的联合分布概率为[14]：

式中：X[0],X[1],…,X[T]表示在0 至T时刻随机变量集合X中的所有节点，xi[t]表示第t个时间片上的第i个节点的状态，πi[t]表示第t个时间片上的第i个节点的父节点的状态。

1.2 DBN可靠性建模

DBN 模型的建立通常包含结构学习和参数学习两个方面。结构学习用以确定初始网络和转移网络的结构，而参数学习则用以确定初始网络和转移网络中各节点的条件概率表。本文根据FTA向DBN 的转换规则实现接触网系统DBN 模型的结构学习和参数学习。将FTA 中的各级事件分别映射为DBN 模型中的各类节点便可完成FTA 向DBN的图形转化，得到DBN 模型的拓扑结构。需要注意的是，伴随着DBN 中时间维度的引入，应该将有向时序边添加进逻辑门的输入事件中，从而完成动态贝叶斯网络中时间片的级联，实现节点状态在时间轴上的拓展。将FTA 中基本事件的发生概率映射为DBN 中根节点的先验概率，同时将逻辑门所表达的逻辑关系映射为DBN 中相应的条件概率表便可完成数值转化，得到DBN 模型的概率参数。表1给出了FTA模型中常用逻辑“与门”和逻辑“或门”向DBN 模型转化的具体规则[15]。转换后DBN 的图形表达中，A(t+ Δt)，B(t+ Δt)，T(t+ Δt)分别表示节点A，B，T在t+ Δt时刻的状态量。可见，通过定义初始网络和转移网络，并经过多个时间片段的延拓，便可求取系统所处状态在某个时间段内的动态特性。条件概率公式中所列的A= 0 表示基本事件A不发生，即元件A处于正常工作状态；而A= 1表示基本事件A发生，即元件A不能正常工作。fA(t)记为元件A的失效概率密度函数，mA(t)记为元件A的维修概率密度函数。基本事件B的概率表示方式与基本事件A相同，此处不再赘述。

表1 FTA逻辑门的DBN转化规则Table 1 DBN conversation rules of FTA logic gates

1.3 复杂系统DBN模型的可靠性分析技术

可靠性工程中常将系统的可靠性定义为：系统在规定的条件下及规定的时间t内能够维持正常工作的能力，通常用可靠度R(t)进行定量描述，它是一个概率值。对于只有正常(0)和失效(1)这2种状态的二态系统来说，系统S的可靠度可以表示为：

在考虑维修因素后，系统的可靠性通常用可用度A(t)进行度量，它表征的是时刻t零部件(或系统)处于正常工作状态的概率。若不对零部件进行维修的话，则其可靠度R(t) =A(t)[16]。通过分析系统的结构和功能，在建立系统的FTA 模型后运用表1 的映射规则便可实现系统DBN 可靠性模型的构建，得到系统初始网络和转移网络的结构及条件概率分布。基于DBN 的一阶马尔可夫性及平稳性，故在任一时间片内的网络结构及各节点间的条件概率分布都是相同的，而零部件所代表的根节点的先验概率则会根据两相邻时间片间节点的转移概率分布在各个时间片上得到更新。

已知零部件Xi在t时刻能够正常工作的先验概率为P{Xi(t) = 0}，那么其在t+ Δt时刻处于正常工作状态的概率便可利用全概率公式更新为：

可见，若给定初始时刻零部件能够正常工作的先验概率P{Xi(0) = 0}，便可利用式(3)扩展得到任意时间片的先验概率。

而在同一时间片内，由根节点的先验概率及各节点间的依赖关系，利用联合概率分布便可正向推理得到系统的可靠度计算表达式：

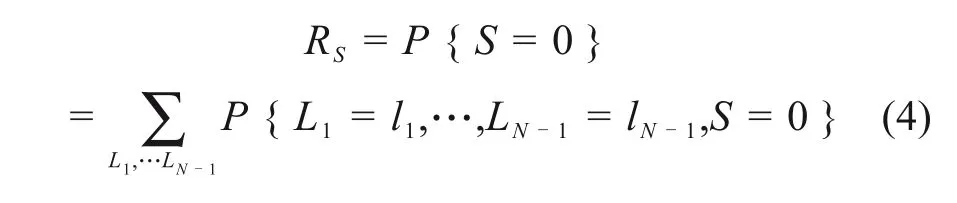
式中用N代表单个时间片内BN 的节点总数。Li(1 ≤i≤N- 1)代表BN 中除了系统节点S外的其余节点，它与FTA 的基本事件和中间事件是相互对应的。li∈{0,1}，它表示的是节点Li的状态取值。

此外，还可以通过反向推理得到单个时间片内某节点Lj发生失效时节点Li发生失效的后验概率计算表达式：

式中：1 ≤k≤N,k≠i≠j。

2 接触网系统DBN模型

2.1 接触网系统FTA模型

根据接触网系统的基本组成结构，可以将其视为由支柱与基础、支持装置、接触悬挂、定位装置这4 个子系统串联构成的系统[17]。而每个子系统又分别由相关的零部件串联构成。假设接触网系统及其各组成零部件均存在“正常”和“失效”这2种状态。因为是串联系统，所以其中的任意一个零部件失效都会导致整个接触网系统失去正常工作的能力。通过对接触网系统的结构分析，构建其FTA 模型，如图1 所示。FTA 中顶事件T表示接触网失效，中间事件M1，M2分别表示支持装置失效、接触悬挂失效。基本事件X1～X11所代表的各基本单元失效名称见表2。表2 中接触网各零部件的失效率λ(/年)及修复率μ(/小时)数据来源于文献[8]对某段电气化铁路接触网长年的故障统计所得。

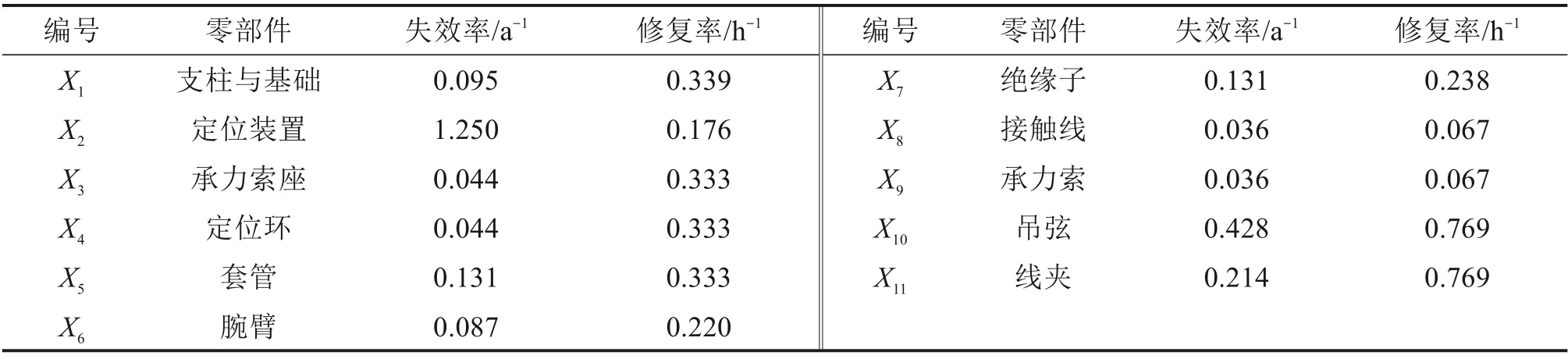
表2 接触网系统基本单元可靠性参数Table 2 Reliability parameters of basic unit of catenary

图1 接触网系统故障树模型Fig.1 Fault tree model of catenary system

2.2 结构学习

在图1 的基础上，利用表1 中给出的FTA 模型向DBN 模型的转化方法建立接触网系统的DBN 拓扑结构，如图2 所示。图2 中，指向节点自身的圆弧箭头表示DBN模型两相邻时间片间的转移网络，它反映了此节点在当前时刻中产生的信念对自身下一时刻的影响；不同节点之间的直线箭头则反映了同一时间片内各节点之间的关联关系。

图2 接触网系统DBN模型Fig.2 DBN model of catenary system

2.3 参数学习

由表1 中FTA 向DBN 的转化规则可以实现接触网系统DBN 模型中同一时间片内静态BN 的条件概率学习和相邻时间片间转移网络的条件概率学习。静态BN 的参数学习较为简单，不再赘述。现针对转移网络的参数学习进行具体叙述。假定接触网系统各零部件Xi都存在2种状态：工作状态0 和失效状态1，且它们的寿命和修复时间均服从指数分布，则与之对应的失效概率密度函数和维修概率密度函数分别为：fi(t) =λie-λit和mi(t) =μie-μit。将其带入表1的条件概率计算公式中，可以通过计算推出Xi从t时刻到t+ Δt时刻的转移条件概率表达式P{Xi(t+ Δt)|Xi(t)}，即：

若暂不考虑零部件Xi的维修问题，此时μi= 0，式(6)中的后面2个表达式便可更新为：

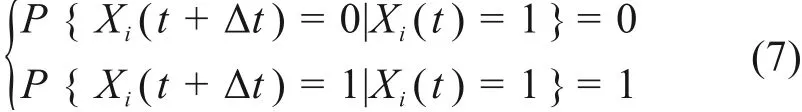
将表2 中各零部件λi和μi的参数值代入式(6)，即可完成接触网系统DBN 模型转移网络的参数学习。

已知零部件在任意时刻处于正常工作状态的先验概率，并结合现有的DBN 推理算法，便可实现对接触网系统可靠性水平的动态估计。

3 接触网系统可靠性分析

接触网系统的可靠性反映了接触网系统各零部件及子系统能够在规定的时间内维持正常工作的能力[17]，可以在一定程度上用它来评估接触网向电力机车供电的稳定性。本文以文献[8]统计的某段电气化铁路接触网的故障数据作为算例，基于DBN 技术对该段铁路接触网的可靠性进行分析。假设初始时刻接触网系统中各零部件Xi均处于正常工作状态，即在t= 0 时刻DBN 模型中各根节点Xi的先验概率为P{Xi(0) = 0}= 1，P{Xi(0) =1}= 0。采用GeNIe 软件建立接触网系统的DBN模型，并基于表1、表2 及式(6)完成网络的结构学习和参数学习后，利用联合树算法进行接触网系统后验概率的推理[18]。

3.1 可靠度估计

在不考虑维修因素的情况下，取时间间隔Δt= 1 月，通过DBN 的正向推理，计算接触网系统在任意时刻处于正常工作状态的概率P{T(t) =0}，即可得到系统可靠度随时间的变化曲线，结果如图3所示。

图3 接触网系统可靠度变化曲线Fig.3 Reliability variation curve of catenary system

由图3可以看出接触网系统的可靠度整体上会随其运行时间的增加而逐渐下降。若不对系统进行定期的维修，其可靠度最终会趋向于0。

下面对接触网、支持装置、接触悬挂、支柱与基础及定位装置的动态可靠度做一对比分析，结果如图4 所示。由图4 可知，随着运行时间的增加，接触网系统各基本组成装置的可靠度均会呈现下降趋势。由于接触网是由这些装置串联构成的系统，因此其下降趋势更为明显。不同装置的可靠度下降速度不同，其中定位装置可靠度的降低对接触网系统可靠度的下降程度影响最大，其次是接触悬挂和支持装置。可以根据定位装置、接触悬挂、支持装置、支柱与基础的可靠性变化规律制定不同的检修周期。

图4 基本装置可靠度变化曲线Fig.4 Reliability variation curves of basic equipment

3.2 可用度估计

考虑维修因素后，同样可以通过DBN 的正向推理计算出接触网系统在任意时刻处于正常工作状态的概率，得到接触网系统可用度随时间的变化曲线如图5所示。

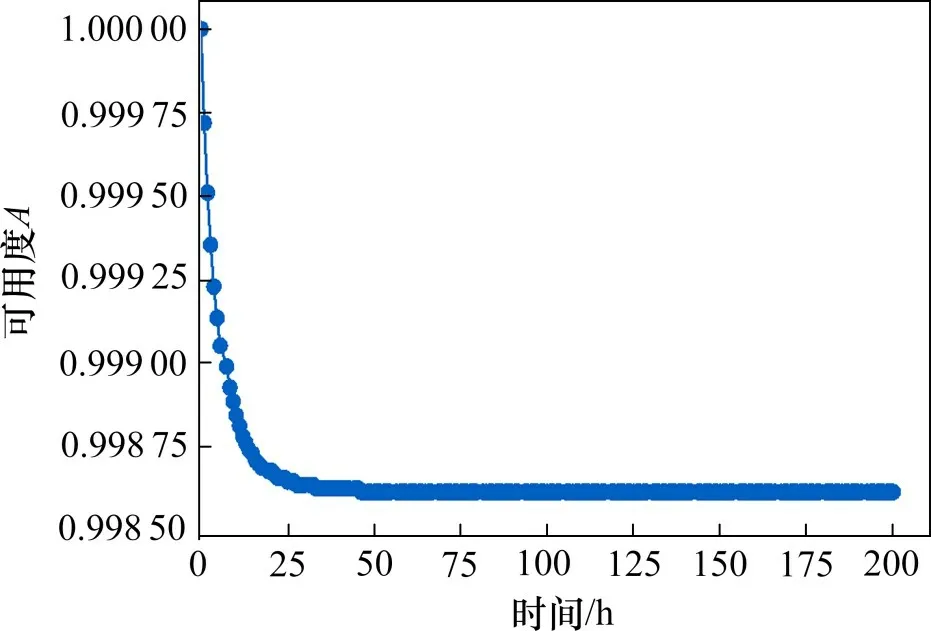
图5 接触网系统可用度变化曲线Fig.5 Availability variation curve of catenary system

由图5可知，在刚投入运行时，接触网系统的可用度逐渐下降，当采取维修措施后，随着时间的推移，系统的可用度逐渐趋于平缓，最终达到稳态可用度，约为0.998 606 933。可以看出算例中的该段铁路接触网具有较高的可用度。由于可用度是在考虑了维修因素的情况下得到的数值，即认为当系统中任意零部件发生故障时，维修人员会立刻对其进行维修，使系统能够恢复正常运行。然而在现实情况中，出于人为因素、环境因素及其他因素的限制，接触网的可用度可能会相较于计算结果值略微偏低一些。

此外，对比图3 和图5 可知，维修因素对接触网系统可靠性的影响较大。因此，为保证接触网系统可靠稳定的运行，对其进行定期维修是很有必要的。

3.3 DBN模型有效性验证

由于DBN 满足“平稳性”和“一阶马尔可夫性”，故对于DBN 中各个时间片内的根节点而言，其在相邻两时间片间的状态转移过程等同于一个齐次马尔可夫过程[19]。文献[8]基于马尔可夫分析法建立了接触网的可靠性分析模型，现将利用本文方法求解得到的接触网系统在运行过程中多个时间点上的可靠度及稳态可用度的计算结果与文献[8]的计算结果进行比较，如表3所示。

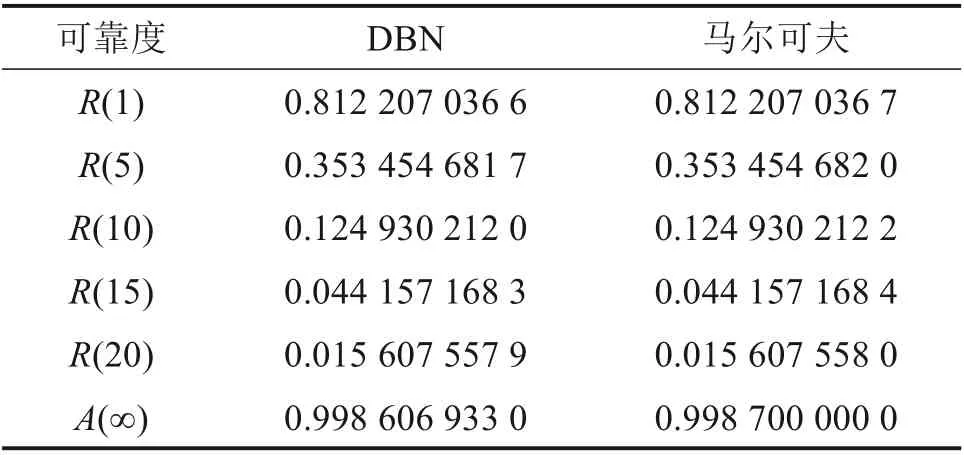
表3 求解结果对比Table 3 Comparison of results

由表3 可以看出利用这2 种方法求解得到的计算结果差异值很小，从而验证了本文所提DBN 方法的有效性和计算结果的精确性。但相较马尔可夫分析方法而言，DBN 方法可以直观地表达系统的组成结构，运用条件概率表表示变量之间的联系。利用变量间的条件独立性可以大大缩小状态空间的规模，有效地避免了马尔可夫分析方法在建模过程中因变量状态数过多而导致的组合爆炸问题[20-21]。而且DBN 还具有反向推理功能，可以实现系统的故障诊断(下节介绍)，这是马尔可夫分析方法所无法比拟的。现在已经有很多成熟的DBN 建模软件[21]，能够实现模型的自动求解，为系统的可靠性分析提供了很大的便利。

3.4 故障诊断

通过分析接触网系统故障后各零部件后验概率值的大小，可以反映出它们在系统中的重要程度。采用DBN 的诊断推理功能，计算出接触网系统在考虑维修因素的情况下进入稳定运行后的某一时刻发生故障时各零部件处于故障状态的后验概率值，即P{Xi(t) = 1|T(t) = 1}，并将各后验概率值按从小到大的顺序进行排序，分析结果见图6。由图6 可知，若该段铁路中接触网系统发生故障，后验概率值排名较为靠前的零部件有：定位装置(X2)、吊弦(X10)、绝缘子(X7)、承力索(X9)、接触线(X8)，它们是接触网系统运行过程中的薄弱环节，故在进行日常检修和维护时需要对这些零部件重点关注，通过提升它们的可靠性来提高接触网系统整体的可靠性。

图6 基本单元的后验概率值Fig.6 Posterior probability value of each basic unit

4 结论

1)将DBN 理论应用于接触网系统的可靠性建模与分析中，可以很好地描述系统的动态特性和可维修性，为接触网系统的可靠性研究提供了一种新思路。

2)在建立接触网系统DBN 模型的基础上，利用DBN 的正向推理能力得到了接触网系统可靠度和可用度随时间的变化趋势，并将计算结果与基于马尔可夫建模方法的求解结果进行横向对比，验证了本文DBN 方法的有效性和计算结果的精确性。

3) 对比可靠度和可用度随时间的动态变化规律可知：在不考虑维修的情况下，接触网系统的可靠度会随服役时间的增加而减小；考虑维修因素后，接触网系统的可用度能在很长的时间内维持在0.998 606 933。所以要保证接触网系统能够可靠地运行，对其故障零部件进行及时地维修是很有必要的。

4)利用DBN 的反向推理能力可以对接触网系统进行故障诊断。诊断结果表明，定位装置、吊弦、绝缘子、接触线和承力索是接触网系统的薄弱环节，因此要加强对它们的检修和维护。