基于客流与列车动态交互的多站 协同客流管控策略评价

孙晟凯，李思杰，刘志钢，赵 源

（1.上海工程技术大学 城市轨道交通学院，上海 201620；2.上海申通地铁集团有限公司 运营管理 中心，上海 201103）

0 引言

随着我国城市轨道交通的快速发展，网络规模逐步扩大，网络化效应日益凸显，客流需求不断增长，特别是在高峰时段，大客流现象普遍存在，与运输能力之间的矛盾突出。为了解决大客流问题，需要采取必要的客流管控手段，以达到提升运营安全的目的。

目前的研究成果多集中在如何科学编制客流管控方案上。部分学者从车站客流管控的角度出发进行研究，如康亚舒[1]以北京复兴门站为例，对车站客流阈值进行分析，确立了客流控制方案；Xu等[2]以不同需求场景下车站服务能力为研究对象，对车站乘客出行过程进行分析，得到了车站客流控制的详细方案。还有部分学者从线路整体客流管控的角度出发，如谢丽平[3]基于城市轨道交通服务能力与出行需求的匹配关系，以上车人数最大化和乘客总延误时间最小化为目标，提出了多站协同客流控制模型；Shi等[4]考虑客流的动态特性以总乘客等待时间最小为目标，对线路多站协同客流管控策略优化；杨静等[5]基于客流在车站间的传播效应，以乘客总延误时间最小为目标构建模型，并引入滚动时域控制方法，实现多站协同限流实时动态控制。在客流管控实施效果评价方面，目前相关研究成果较少。江志彬等[6]从定性与定量2个角度考虑，基于站台人数变化、乘客延误时间、客运周转量等指标建立了限流指标评价体系。禹丹丹等[7]从车站、线路、网络3个层次构建限流指数，用以评估限流方案。然而，以上成果没有充分考虑客运组织与行车组织相结合的实际情况，缺乏对措施实施效果综合量化的方法。

基于实际客流数据与列车运行数据，以车站限流和列车跳停的组合方案为研究重点，构建客流与列车的动态交互模型，得到列车满载率、站台聚集最大乘客数、乘客出行延误时间3类指标；在此基础上，从大客流疏解效率、站台客流拥挤风险和列车满载率均衡性3个方面，提出城市轨道交通协同客流管控策略综合评价指数的概念与计算方法，综合评价不同列车开行方案与不同限流方案实施后大客流问题的改善效果。

1 客流与列车动态交互模型

1.1 模型假设与数据定义

为便于问题研究，提出以下假设：①进入轨道交通系统内部的乘客不存在放弃出行情况，即出行过程中不会改变出行方式；②在列车跳停开行的情形下，乘客选择直达目的车站的列车出行；③若列车跳停开行，则满足同一列车不能连续跳停2站、一个车站不能连续跳停2次列车的开行要求；④在安全运行的前提下，列车允许一定程度的超载。

客流与列车动态交互模型（以下简称“模型”）需要输入列车运行数据、限流数据、客流出行OD数据和列车编组参数。通过列车时刻表的描述，确定所有列车在每个车站的到发时刻、区间运行时间、停站时间和跳停属性；通过限流策略确定限流车站和限流强度；通过自动售检票系统（AFC）提取原始乘客OD数据，经过统计得到每单位时间 （1 min）起讫点客流人数。模型输入数据指标定义如表1所示。

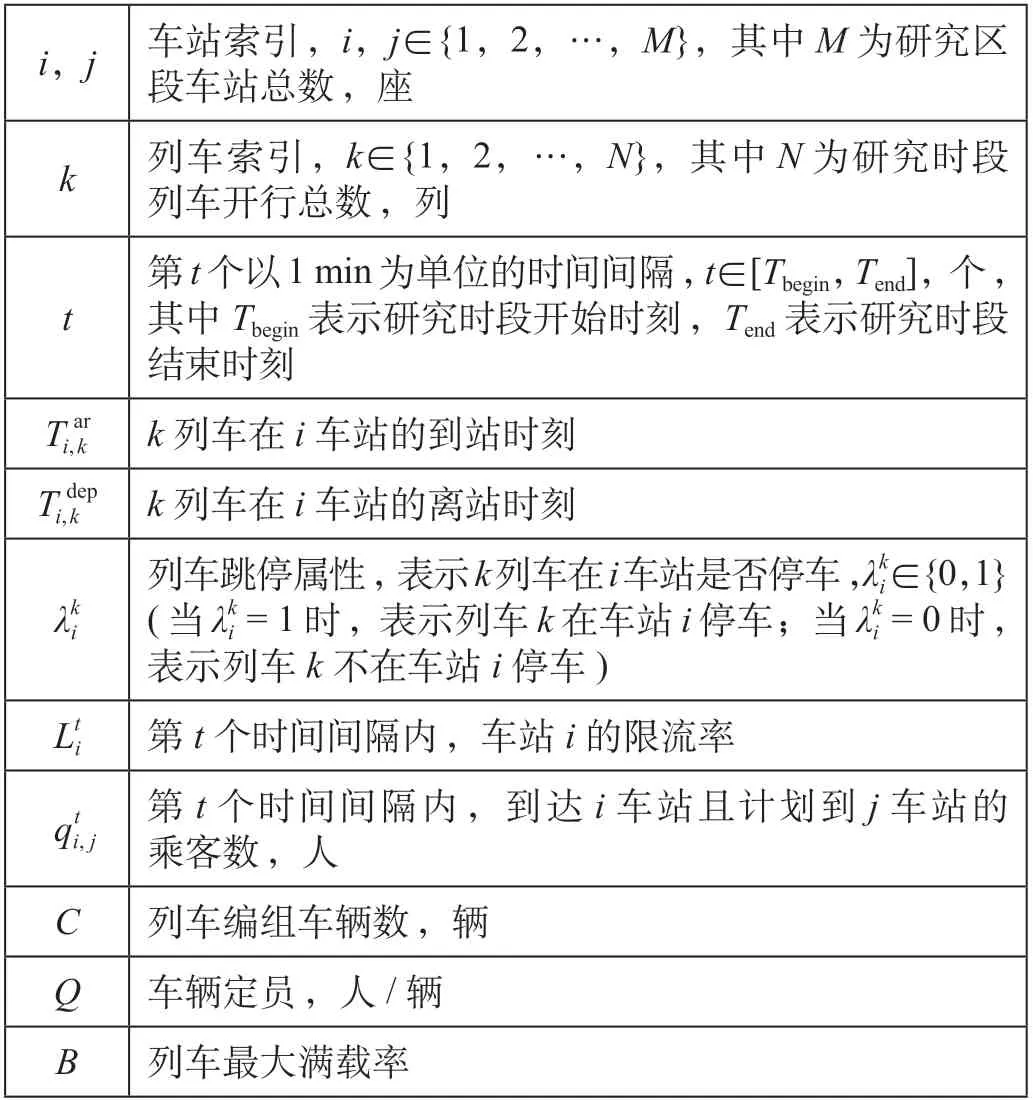
表1 模型输入数据指标定义Tab.1 Definition of model input data index

1.2 输出指标

模型将输出3类指标：列车各区间的满载率、站台聚集最大乘客数和乘客的出行延误时间。通过这3类输出指标可以精细化描述采取限流策略和列车跳停方案后的运营状态。

（1）列车满载率。列车满载率是衡量列车运力利用情况的重要指标。列车k发车到首站区间为空车开行状态，区间载客量为0；其余区间（i≥1）开行时，由于车站进行了乘客上下车作业，（i，i+1）区间列车满载率由（i-1，i）区间列车满载率、i站上车和下车乘客决定。列车满载率计算公式为

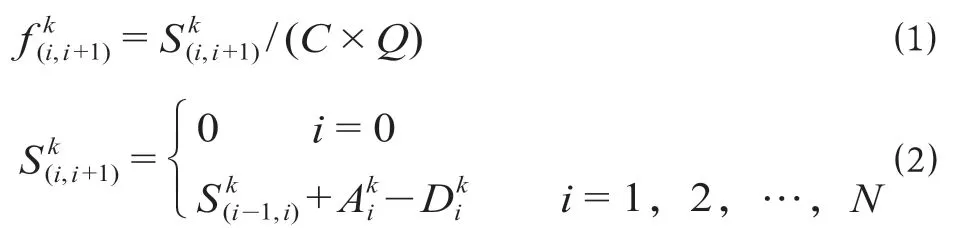
式中：为k列车在（i，i+1）区间的满载率；为k列车在（i，i+ 1）区间的载客量，人；为k列车到达i车站后的乘客上车人数，人；Dik为k列车到达i车站后的乘客下车人数，人。

（2）站台聚集最大乘客数。站台聚集最大乘客数是反映车站的乘客服务水平和站台安全性的重要指标。列车采取跳停开行方案下，在上一班列车在该站未停车，且本列车到站停车乘客全部顺利下车后，站台聚集乘客最多。站台聚集最大乘客数计算公式为

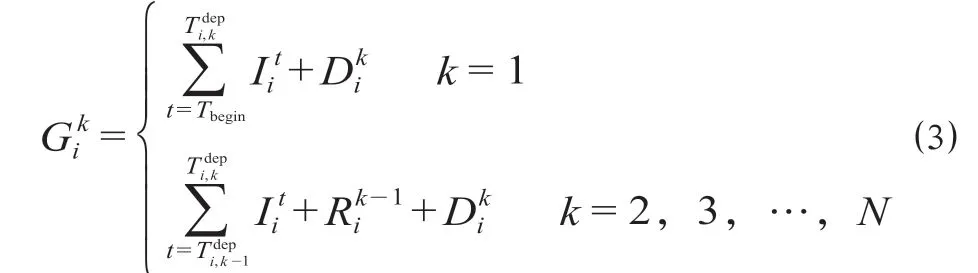
式中：Gik为列车k到达车站i后站台聚集最大乘客数，一般分为3类，分别是到达站台乘客、未能登上上一班列车而滞留乘客和到站下车乘客，人；Iit为第t个时间间隔内，车站i的进站乘客数，人；Rik-1为列车k-1到达车站i后因列车容量限制而不能上车的站台滞留乘客数，人。

（3）出行延误时间。乘客出行延误时间为在整个高峰时段[Tbegin，Tend]内，乘客出行延误时间的累计。乘客出行延误时间计算公式为

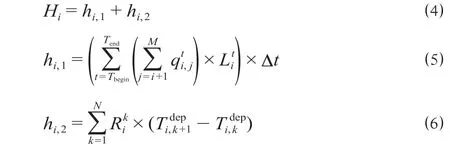
式中：Hi为i车站乘客出行延误时间，分为2部分，分别是限流导致的站外延误时间hi,1，min，列车跳停或运力不足导致的站台延误时间hi,2，min；Δt表示车站i限流率计算的时间间隔，min。

1.3 模型构建

针对时段[Tbegin，Tend]，从第1列车到达第1个车站开始，对每列车经过各个车站进行循环计算，得到乘客与列车动态交互过程中上车、下车、候车和滞留人数情况，最终输出3类评价指标。流程如下。

步骤1：输入列车运行数据（列车时刻表、跳停属性λik），列车参数（列车编组数C、车辆定员Q、列车最大满载率k），限流参数Li t，客流出行OD数据qti,j。

步骤2：数据预处理，依次计算第t个时间间隔内，i车站的进站客流和进站乘客中计划到j车站的乘客数。计算公式为

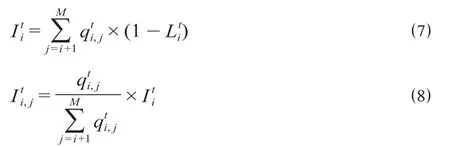
式中：表示进站乘客中计划到j车站的乘客数，人。

步骤3：算法初始化。令i= 1，k= 1。

步骤4：根据列车运行过程和乘客出行过程，计算各车站的客流状态数据。

i车站站台等待k列车的乘客中计划到j车站的乘客数计算公式为

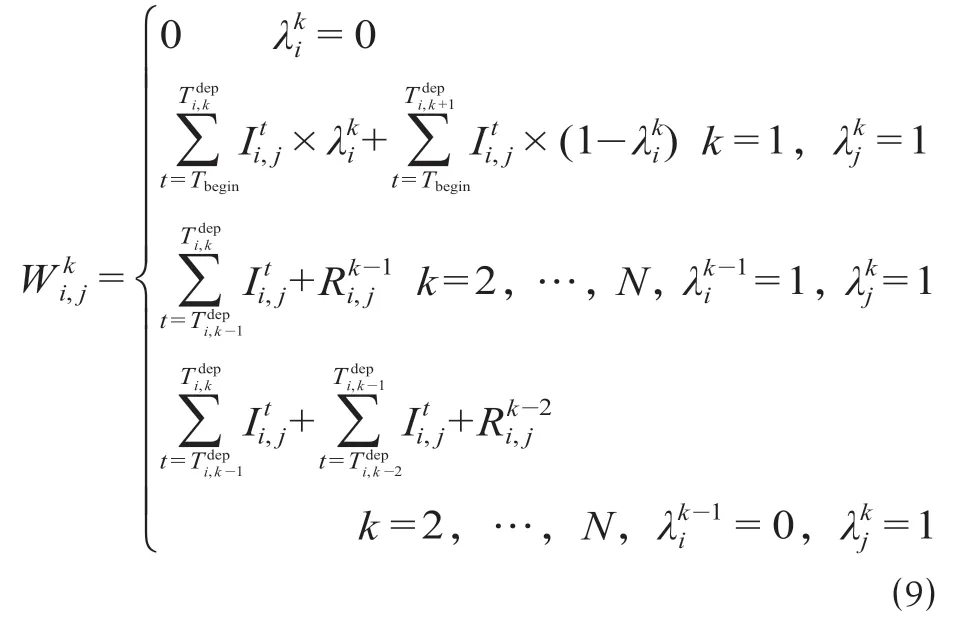
式中：W ki,j表示i车站站台等待k列车的乘客中计划到j车站的乘客数，人。

k列车在i车站乘客下车人数Dik计算公式为

式中：Atj,i表示t时刻在j车站计划到i车站的上车乘客数，人。

根据列车到站后的剩余运力是否足够，分类计算k列车在i车站乘客上车人数，计算公式为

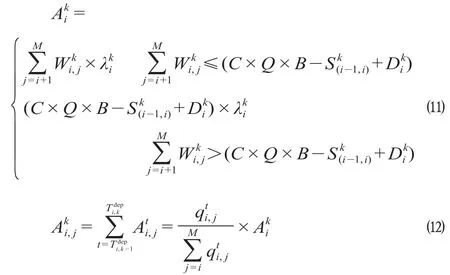
式中：Ati,j表示k列车在i车站计划到j车站的上车乘客数，人；表示列车到站后的剩余运力。

k列车离开i车站后站台滞留乘客人数分为2类：一类是因车辆满载而被动滞留的乘客；另一类是因该站跳停或到达站跳停而主动滞留的乘客，计算公式为

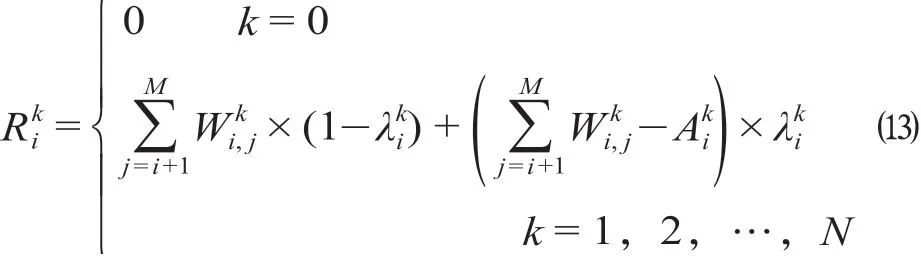
式中：Rik表示k列车离开i车站后站台滞留乘客人数，人。

步骤5：根据公式⑴至公式 ⑹ 分别计算区间列车满载 率，站台聚集最大乘客数，乘客的出行延误时间Hi。

步骤6：令i=i+ 1。若i＜M，返回至步骤3，计算列车k到达下一站站台和区间列车载客的状态；否则，转至步骤7。

步骤7：令k=k+ 1。若k≤N，令i= 1，返回至步骤3，计算下一列车到达所有站乘客与区间载客的状态；否则，转至步骤8。

步骤8：计算完毕，输出所有描述乘客列车交互过程的3类指标，算法结束。

模型运算结果与采取的客流管控策略完全匹配，客流控制下的AFC客流数据相较于现场客流控制数据更精准，更能准确得到乘客进站、上下车过程中各环节客流数据，并能够通过运算得到3类指标值的对比分析，评价最优客流管控策略。

2 多站协同客流管控策略综合评价

由于不同的协同客流管控策略下，模型运算所输出的N列车经过M个车站的3类指标是区间和车站微观层面的指标，无法从线路层面的角度总体评价客流管控效果。为了反映不同协同客流管控策略的线路层面效果，需要对模型运算的所有区间和车站指标进行综合评价。

2.1 综合评价指数的定义

综合评价指数是从线路的角度对协同客流管控策略缓解大客流问题效果的评估[8]，以多个层面评价为原则，对线路各站和区间客流拥挤情况影响要素进行探析[9]，确定了主要3个影响要素：大客流疏解效率、站台客流拥挤风险和列车区间运力均衡度，3者的合成值作为综合评价指数的评价结果。综合评价指数越大，则限流策略越优。

2.2 综合评价指数影响要素计算

综合评价指数影响要素由乘客与列车交互模型输出的指标进行量化得到，由于各要素评价值的量纲单位不同，故对数据进行无量纲化预处理。为了使预处理后数据能较真实地反映原指标值之间的关系，采用全局改进归一化方法作为指标一致化及无量纲化方法，对3类指标值进行预处理[10]。综合评价指数的影响要素评价值计算如下。

（1）列车区间运力均衡度。列车区间运力均衡度取决于线路上各列车在各区间的满载率离散程度。在列车运输能力约束下，列车满载率离散程度越大，则列车区间运力均衡度越小。计算公式为

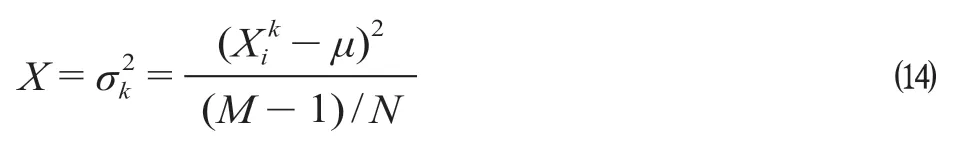
其中

式中：X表示列车区间运力均衡度；σk2表示Xik的总体方差；μ表示Xik的平均值；Xik表示列车k在区间（i，i+1）的列车满载率指标值预处理值。

（2）站台客流拥挤风险。线路站台客流拥挤风险取决于线路上各车站站台聚集最大乘客数Gik。在站台最大承载能力的约束下，i车站站台聚集最大乘客数越大，则站台客流拥挤风险越大。在客流高峰时段内，线路站台客流拥挤风险计算公式为

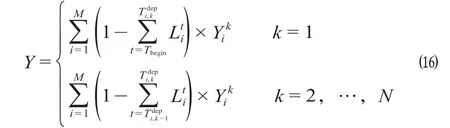
式中：Y表示线路站台客流拥挤风险；Yik表示列车k在车站i站台聚集最大乘客数Gik指标值预处理值。

（3）大客流疏解效率。线路大客流疏解效率取决于线路上各车站乘客出行延误时间Hi。乘客出行延误时间越小，则该站的大客流疏解效率越高；当乘客出行延误时间为0，即该站未发生客流拥挤时，大客流疏解效率为0。在客流高峰时段内，线路大客流疏解效率Z计算公式为

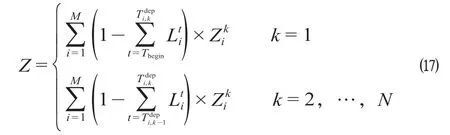
式中：Z表示线路大客流疏解效率；Zik表示车站i乘客出行延误时间Hi指标值预处理值。

2.3 综合评价指数的计算

根据2.2节计算过程可知，大客流疏解效率值、站台客流拥挤风险值、列车区间运力均衡度值与综合评价指数值负相关。为了使其呈正相关关系，对各影响要素评价指标取倒数。由于加法合成或多目标平均法指标间可以相互替代，较好的指标能够弥补较差指标，具有补偿作用，难以显出指标值之间的大小差距，从而影响对各方案的综合评价，而乘法合成法强调指标全面发展，若某项指标偏低则导致总体评价值降低[11]。因此，采取乘法合成法计算客流管控策略综合评价指数值，计算公式如下。

式中：E表示客流管控策略综合评价指数值，E值越大反映方案越优。

3 实证分析

以上海轨道交通9号线（以下简称9号线）为例进行实证分析，选取该线路某工作日客流早高峰（7 : 30—8 : 30）为研究时段，松江南站—杨高中路上行方向（共26站）为研究区段，通过不同列车跳停开行和不同限流策略的组合，进行3类指标和综合评价指数对比分析，验证评价方法的可行性和有效性。

3.1 基本参数

（1）列车运行参数。9号线采用城市轨道交通标准A型列车，列车运行参数如表2所示。9号线早高峰为了缓解线路整体客流压力，部分列车在松江大学城和洞泾站设置跳停。根据实际客流场景设定开行方案1 （跳停）和开行方案2 （不跳停），不同列车开行方案如图1所示。列车运行时刻表可根据发车间隔时间、区间运行时间、停站时间以及跳停方案递推得到，作为列车运行数据输入模型。

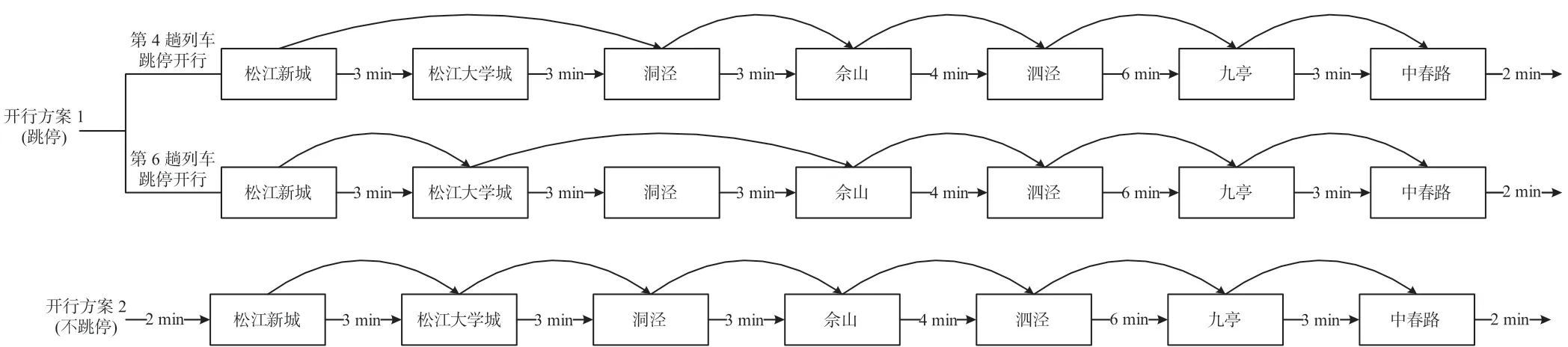
图1 不同列车开行方案Fig.1 Different train working diagrams

表2 列车运行参数Tab.2 Train operation parameters

（2）客流参数。通过对9号线AFC数据进行预处理得到线路客流数据，将9号线宜山路、徐家汇等换乘车站换入9号线上行方向的客流量与进站客流量加和作为对应站的客流量，将换出客流量与出站客流之和作为对应站的下车客流量，并以 1 min为时间间隔将输入的OD乘客需求分组记录，得到客流出行OD数据输入模型。

（3）限流参数。9号线早高峰常态化协同限流车站共有4座，分别为佘山站、泗泾站、九亭站和世纪大道站。根据实际客流场景设定限流策略1 （采取限流）与限流策略2 （未采取限流）作为限流方案数据输入模型，各限流策略限流率参数如表3所示。为了验证高峰时段客流管控策略综合评价指数适应性，将不同的列车开行方案和不同限流策略两两组合可得客流管控策略如表4所示。

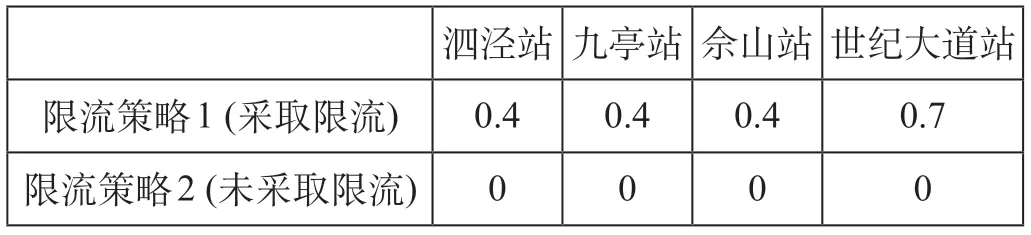
表3 限流率参数Tab.3 Flow restriction rate parameters

表4 客流管控策略Tab.4 Passenger flow control strategies

3.2 计算结果分析

3.2.1 模型运算结果分析

（1）列车满载率。用热力图表示每趟列车经过各区间的满载率大小，不同客流管控策略下列车满载率如图2所示。由图2可知，9号线早高峰时段未采取限流时，如策略B和策略D，多次发生列车满载率达到1.3的情况；采取限流或列车跳停开行后，如策略A和策略C，红色高满载率密集度明显下降；策略A同时采取限流和列车跳停开行，红色高满载率发生情况最低。说明在大客流情况下，采取限流和列车跳停开行能有效减少部分列车满载率过高情况的发生。

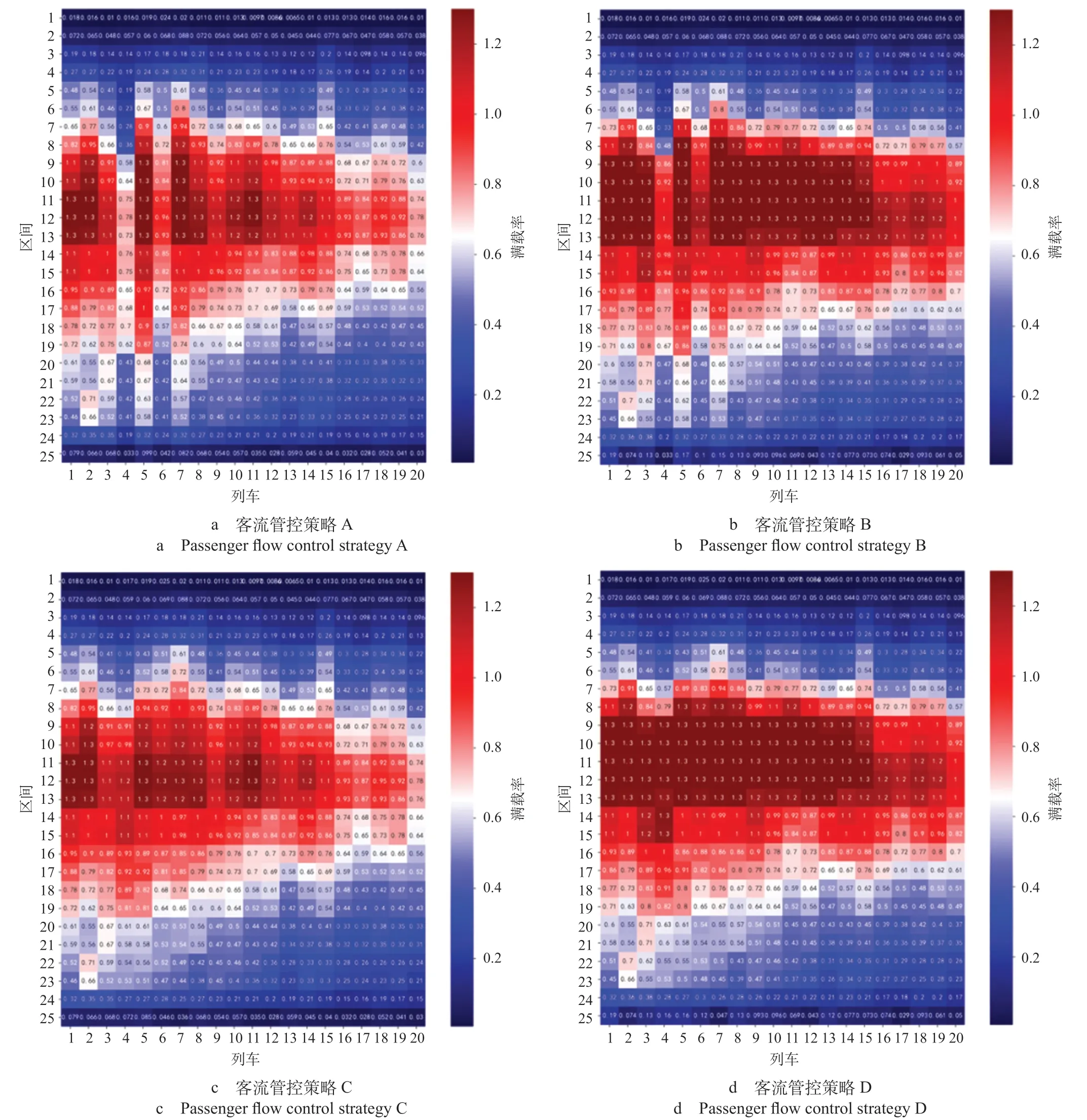
图2 不同客流管控策略下列车满载率Fig.2 Train full load rates under different passenger flow control strategies

（2）站台聚集最大乘客数。用气泡图表示每趟列车经过各车站的站台聚集最大乘客数，气泡越大站台聚集乘客数越多，不同客流管控策略下站台聚集最大乘客数如图3所示，图3中红色气泡表示超过站台设计最大承载能力（≥800人）的情况。由图3可知，9号线高峰时段，第1辆、第2辆车各站站台聚集最大乘客数明显多于其他列车，上行方向松江南站—合川路站站台聚集最大乘客数明显多于川路站—世纪大道站，与车站大客流的时空不均衡性特征一致。在采取限流或列车跳停开行后，出现大量气泡缩小情况，且4个常态限流车站最为明显，采取限流后超过站台设计最大承载能力发生次数明显降低。

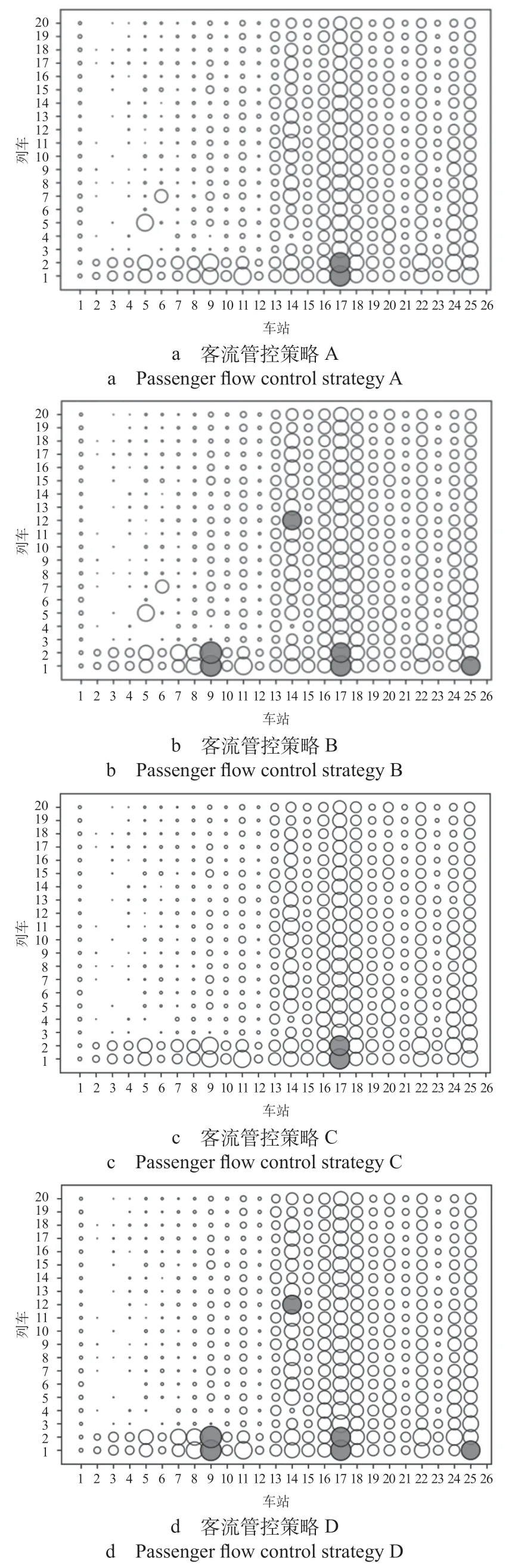
图3 不同客流管控策略下站台聚集最大乘客数Fig.3 Maximum number of passengers gathered at platforms under different passenger flow control strategies

（3）乘客出行延误时间。用气泡图来表示每趟列车经过各车站的乘客出行延误时间，气泡越大乘客出行延误时间越长，不同客流管控策略下乘客出行延误时间如图4所示。从图4可知，9号线高峰时段，在未采取限流情况下，由于前方限流车站佘山站—九亭站乘客数量增大，导致列车在九亭站—星中路站运输能力不足，发生明显的乘客出行延误现象，与实际情况相符；采取限流策略和列车跳停开行后，出现大量气泡缩小的情况，九亭站—星中路站乘客出行延误有效缓解。

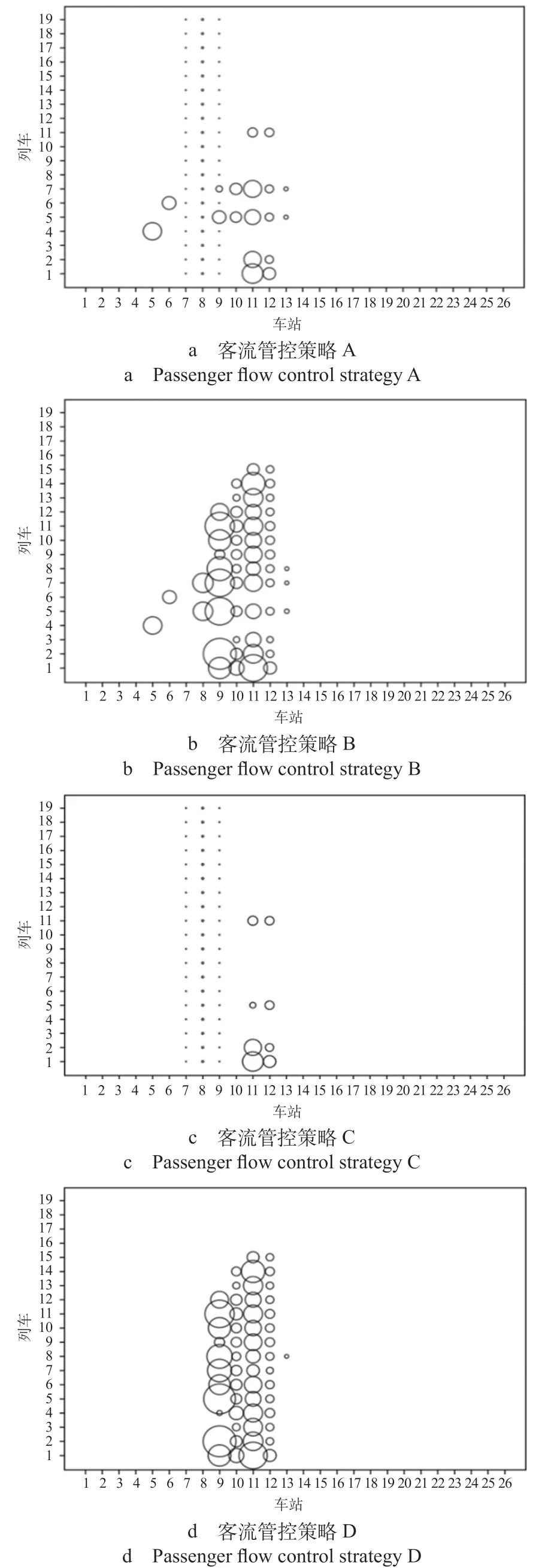
图4 不同客流管控策略下乘客出行延误时间Fig.4 Travel delay of passengers under different passenger flow control strategies

3.2.2 综合评价指数结果分析

各影响因素指标评价值如图5所示。由图5可知，列车区间运力均衡度X、站台客流拥挤风险Y和客流疏解效率Z能够从列车—车站—乘客3个角度反映不同运营方式下各类影响因素评价的优劣，且不同的列车开行方案和不同限流策略下，对列车区间运力均衡度X影响较大。结果得出，客流管控策略A的各类影响因素指标评价值均最高，说明在采取限流—跳停开行方案下，列车区间运力最均衡，站台客流拥挤风险最小，客流疏解效率最高。

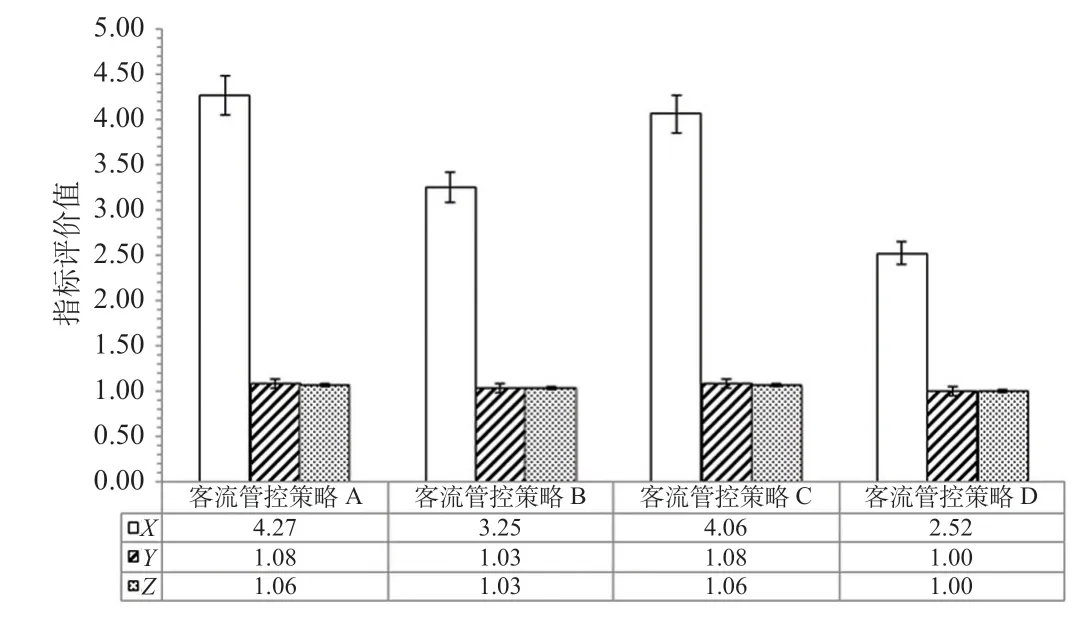
图5 各影响因素指标评价值Fig.5 Evaluation value of each influencing factor index

各客流管控策略综合评价指数值如表5所示。综合评价指数能够从线路整体的角度反映在大客流情况下，对各跳停开行方案下不同限流策略的优劣评价结果。根据表5，客流管控策略A综合评价指数值最大，缓解大客流效果最优；采取限流策略或列车跳停开行方案均可一定程度上缓解线路大客流现象。

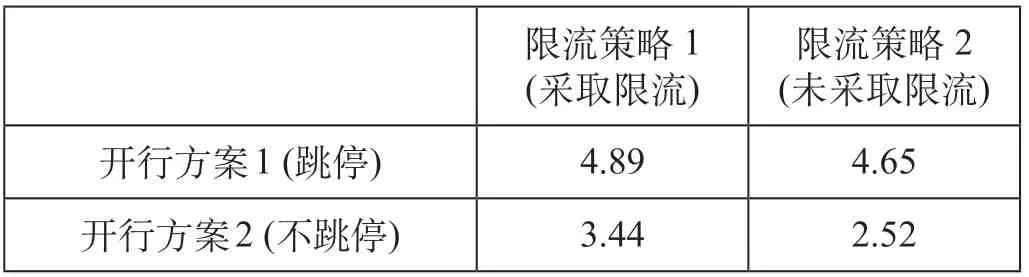
表5 各客流管控策略综合评价指数值Tab.5 Comprehensive evaluation index values of each passenger flow control strategy

4 结束语

基于客流与列车动态交互的多站协同客流管控策略评价方法，在充分考虑了列车跳停开行和多站协同限流情况下，构建客流与列车动态交互模型获取列车满载率、站台聚集最大乘客数、乘客出行延误时间3类指标，能有效反映高峰时段车站和列车的客流时空分布特征，提出的综合评价指数可从线路整体角度综合量化客流管控策略实施效果。案例实证分析中，客流与列车动态交互模型与评价方法适用于不同客流管控策略，评估结果有效，可为客流管控策略的制定与优化提供指导意见和数据支持。该方法适用于单线多站协同客流管控策略的评估，未来研究可从网络层面进行客流的溯源分析，进一步考虑客流管控措施对乘客路径选择的影响。