地铁进站客流量 SARIMA 与 GA-BP神经网络组合预测模型

2021-12-22强添纲裴玉龙

铁道运输与经济 2021年12期

强添纲，刘涛，裴玉龙

（东北林业大学交通学院，黑龙江哈尔滨 150040）

0 引言

随着城市经济的不断发展，越来越多的城市选择建设地铁来缓解当地的交通拥堵。城市地铁网络规模不断扩大、客流量不断增加等因素对地铁的运营管理提出更高的要求，如何利用地铁客流数据准确预测未来一段时期的客流量，对于制定合理的运营管理策略尤为重要。

目前，客流量预测方法主要分为基于时间序列的统计预测模型、基于非参数的预测模型和组合预测模型。基于时间序列的预测模型方面，赵鹏等[1]利用季节求和自回归移动平均模型（SARIMA）对北京地铁的端点站、中间站、换乘站及接驳站进行客流预测，结果表明SARIMA模型有较高的预测精度。李洁等[2]利用SARIMA模型预测广州南站、小榄站的发送客流量，与随机森林（RF）、支持向量机（SVM）等预测方法对比发现在预测步长较大时SARIMA模型最优。马超群等[3]利用求和自回归移动平均模型（ARIMA）进行拟合，并与自回归模型（AR）、支持向量线性回归模型（SVR）、反向传播（BP）神经网络进行对比，发现在不同时间粒度下ARIMA模型平均预测精度最高。王莹等[4]利用SARIMA模型对北京地铁进站客流量进行预测，结果显示模型预测的平均误差为0.3%。

基于非参数预测模型方面，Du等[5]提出一种比传统客流预测模型效果更好的深度不规则卷积残差（DST-ICRL）长短记忆（LSTM）网络模型。Liu等[6]提出了一种端到端的深度学习架构（DeepPF）来预测地铁客流量，研究结果表明DeepPF拥有较高的预测精度。Li等[7]提出一种多尺度径向基函数（MSRBF）网络预测地铁客流量，实验表明该模型预测精度高于其他智能模型。李洁等[8]根据时间序列数据建立循环神经网络（RNN）预测模型，结果表明RNN模型的预测精度与训练数据的类型和数量存在较大关系。谷金晶等[9]利用公交IC卡上车数据构建BP神经网络和径向基函数（RBF）神经网络，试验结果表明RBF神经网络预测效果更好。

组合预测模型方面，Wei等[10]提出了一种将经验模式分解（EMD）和BP神经网络相结合的混合EMD-BPN方法用于地铁客流量预测。Dimitriou等[11]提出一种基于自适应混合模糊规则系统（FRBS）的城市干道交通流短期预测方法，试验结果表明该方法优于传统的遗传算法。Zheng等[12]基于BP神经网络、RBF神经网络和贝叶斯定理构建贝叶斯组合预测模型，结果表明该模型预测结果较好但鲁棒性较差。Hong等[13]提出一种基于SVR模型和连续蚁群优化算法（SVRCACO）的城市间交通流短期预测模型，结果表明该模型预测结果优于SARIMA模型。赵建立等[14]提出一种基于卷积神经网络（CNN）与残差网络（ResNet）的组合预测模型（ResNet-CNN1D），结果表明该模型预测精度更高。林浩等[15]基于遗传算法（GA）和粒子群算法（PSO）构建GAPSO-SVM模型，实验显示GAPSO- SVM模型有较高的预测精度。黄益绍等[16]基于粗糙集（RS）和改进粒子群（IPSO）构建优化支持向量机（RS-IPSOSVM）的公交客流预测方法，结果表明该方法简化了训练样本，解决了SVM参数选择的盲目性。

地铁进站客流是具有一定周期性的时间序列数据，考虑SARIMA模型预测效果较好且所需数据较少，传统研究一般使用该模型对客流进行预测；而随着计算机技术的迅猛发展，且为解决SARIMA模型无法考虑相关因素对进站客流量影响的缺点，越来越多学者选择使用神经网络等算法预测客流量。考虑神经网络等算法容易出现局部极小化等问题，在已有研究基础上提出一种基于SARIMA模型和GA-BP神经网络的地铁进站客流组合预测模型。研究先分别对SARIMA模型和GA-BP神经网络参数进行标定，在获取到SARIMA模型和GA-BP神经网络预测值的基础上，结合SARIMA模型的最大季节回归多项式个数明确组合模型因变量个数来确定组合模型的权重值，并最终建立线性组合预测模型。

1 线性组合预测模型建立

1.1 季节求和自回归移动平均模型

考虑季节求和自回归移动平均（SARIMA）模型能够很好地描述客流量数据的趋势变化和季节周期特性，且城市地铁进站客流量属于周期性的时间序列数据，因而选择该模型作为子模型对进站客流预测。SARIMA模型是在自回归移动平均模型的基础上考虑到时间序列周期变化的季节性所带来不平稳现象做出改进，通过对含有季节性周期的时间序列进行季节差分的方法将其化为平稳序列。SARIMA（p，d，q）（P，D，Q）S计算公式为

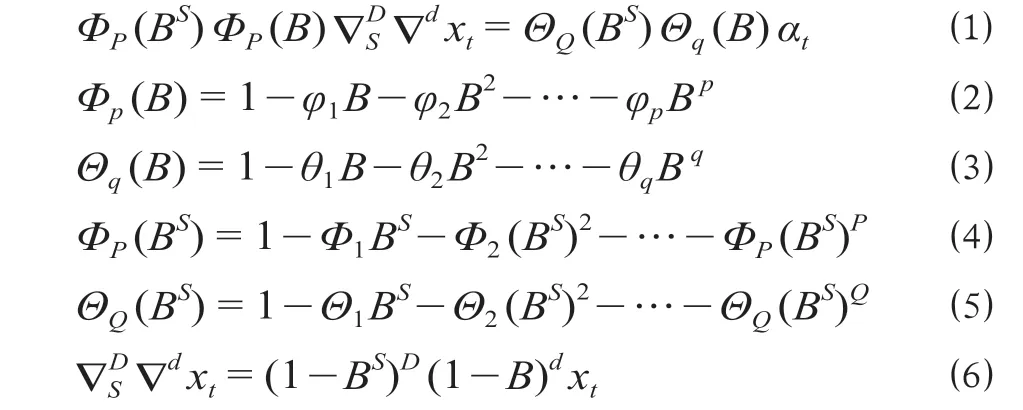
式中：Φ1，Φ2，…，ΦP为季节自回归系数；φ1，φ2，…，φp为非季节自回归系数；Θ1，Θ2，…，ΘQ为季节移动平均系数；θ1，θ2，…，θq为非季节移动平均系数；αt为t时刻的白噪声；∇SD为D阶季节周期为S的差分算子；∇d为d阶差分算子；xt为过去各期误差αt，αt-1，…，α1的线性组合；B为滞后算子。

其中，上述公式所对应的ΦP（BS）为P阶季节自回归系数多项式；Φp（B）为p阶自回归多项式；ΘQ（BS）为Q阶季节移动平均多项式；Θq为q阶移动平均多项式；为平稳的时间序列。

1.2 GA-BP神经网络模型

传统SARIMA模型无法考虑地铁发车次数等因素对进站客流的影响，为研究不同因素对客流的影响，研究选择使用GA-BP神经网络作为子模型对地铁客流进行预测。BP神经网络是一种利用梯度下降法使其实际输出值和期望输出值误差均方差为最小的多层前馈神经网络，正因如此BP神经网络预测时容易陷入局部最小值。研究选择使用遗传算法（GA）获取BP神经网络的初始权重值和阈值，降低BP算法陷入局部最小值可能性[17-18]， GA-BP算法流程如图1所示。

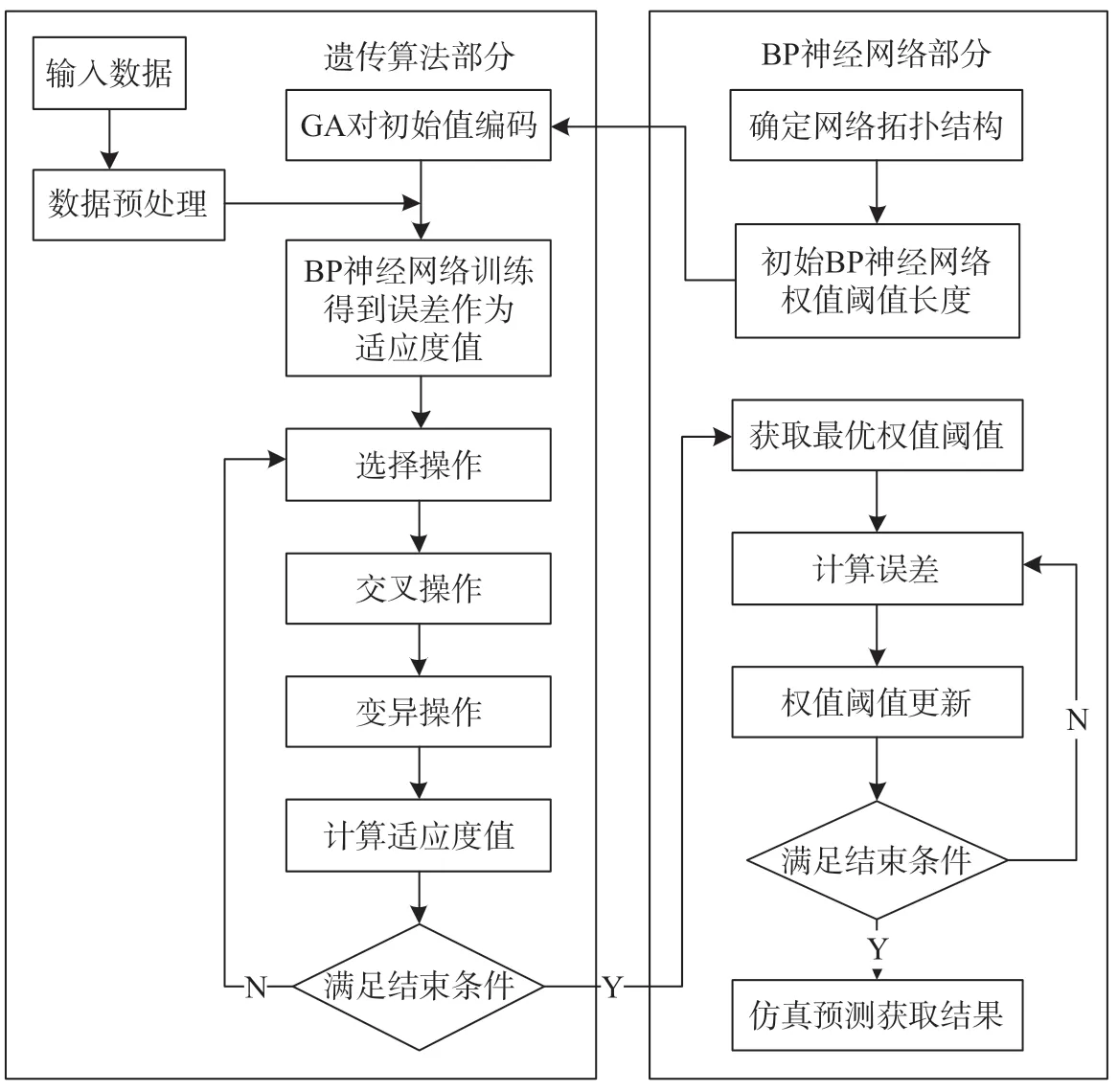
图1 GA-BP算法流程图Fig.1 Flow chart of GA-BP algorithm

模型以累计误差最小为目标，计算公式为

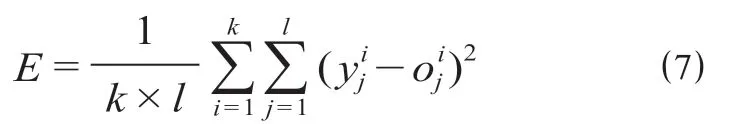
式中：E为累计误差；为BP神经网络预测第i个样本下第j维变量的预测值；为第i个样本下第j维变量对应的实际值；l为输出变量的维数；k为训练样本个数。

GA-BP神经网络训练步骤如下。

（1）步骤1：确定网络拓扑结构。确定网络输入层节点数a，隐含层节点数b，输出层节点数c，输入层与隐含层神经元之间的连接权值，隐含层与输出层连接权值，隐含层阈值，输出层阈值

（2）步骤2：随机化初始种群。个体采用实数编码方式，由输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值4部分组成，具体构成如公式（8）所示。

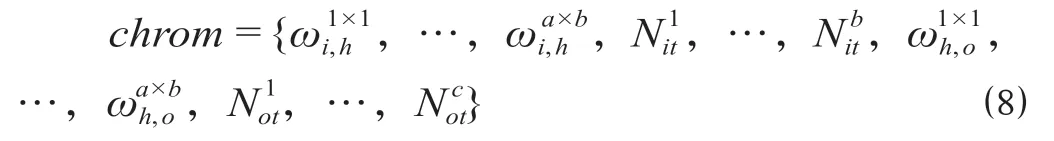
（3）步骤3：确定适应度函数。利用BP神经网络预测结果与实际结果之间误差的绝对值之和作为个体适应度值f，其计算公式为

式中：yi为输出层第i个节点的预测值；oi为输出层第i个节点的实际值。

（4）步骤4：选择操作。研究选择轮盘赌法，通过适应度比例确定个体i的选择概率pi，计算公式为

式中：Fi为个体i修正后的适应度值；fi为个体i的适应度值；k1为系数；n为种群个体数目。

（5）步骤5：交叉操作。研究选择实数交叉法，即第m个染色体gme和第l个染色体gle在e位交叉，交叉的计算公式为

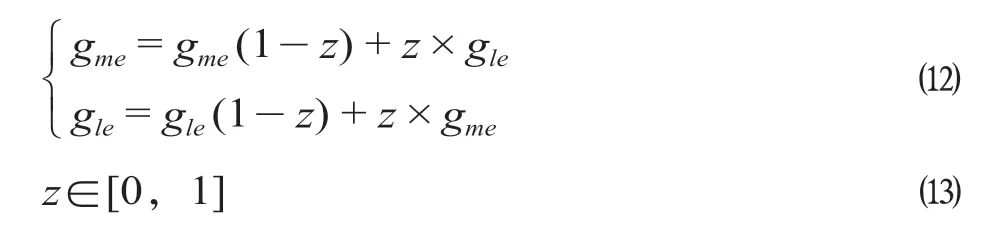
式中：z为[0，1]区间的随机值。

（6）步骤6：变异操作。选取第i个个体的第e个基因gie进行变异，考虑基因变异是一种随机现象，采用一个在[0，1]区间的随机值r来决定该基因的变异方式，具体变异方式如下。

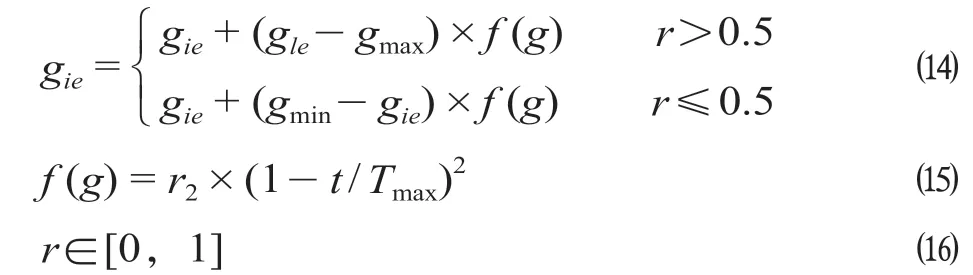
式中：gmax为基因gie的上界；gmin为基因gie的下界；r2为一个随机数；t为当前迭代次数；Tmax为最大迭代次数。

（7）步骤7：计算适应度函数值。如果满足算法结束条件则输出优化的权值和阈值，反之则返回步骤4。

（8）步骤8：隐含层计算。隐含层激励函数选择tansig函数，计算公式为

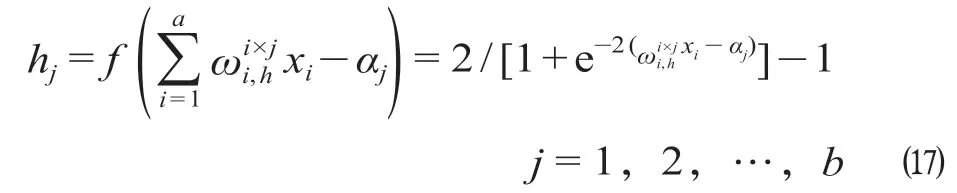
式中：xi为第i个个体输入值；αj为第j个系数。

（9）步骤9：输出层计算。

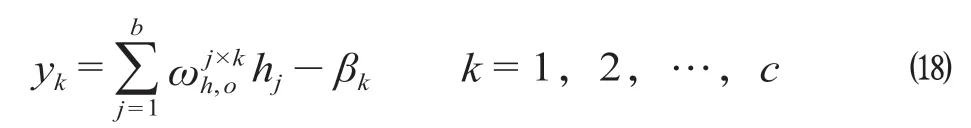
式中：βk为第k个系数。

（10）步骤10：判断是否满足结束条件，若不满足结束条件则返回步骤8。

1.3 组合预测模型

尽管利用遗传算法优化BP神经网络的初始权值和阈值，但该模型依然存在陷入局部最小值问题。为解决这一问题并提高模型的预测精度，研究在SARIMA模型和GA-BP神经网络预测值的基础上进一步地修正预测值。研究考虑时间序列季节性波动的特性，结合SARIMA模型的季节周期S、季节自回归系数多项式对应阶数P和季节移动平均多项式对应阶数Q选取某一历史时间段内的多个子模型预测结果，并根据其预测精度确定组合预测模型对应的权重值。

考虑SARIMA模型可以确定该时间序列数据是以S个步长为一个季节周期，其组合预测模型构建的具体思路如下。

（1）先明确需要预测数据在一个季节周期内的具体位置（如一个星期内的第4位则是星期四），以该位置为原点统计出训练集最近v个季节周期内相同位置2个模型的预测值，并计算其对应的平均绝对百分比误差（MAPE），具体计算公式为

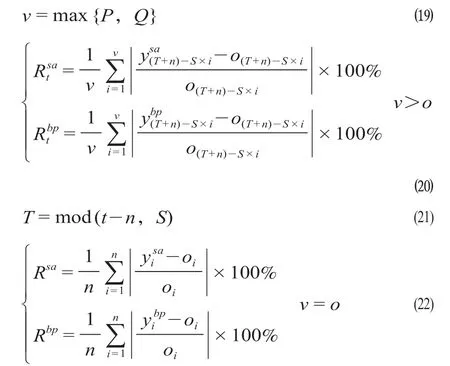
式中：Rtsa为SARIMA模型预测第t个数据的MAPE；Rtbp为GA-BP神经网络预测第t个数据的MAPE；Rsa为SARIMA模型在训练集下的MAPE；Rbp为GA-BP神经网络在训练集下的MAPE；为 SARIMA模型预测步长为（T+n） -S×i时的预测值；为GA-BP神经网络预测步长为（T+n） -S×i时的预测值；o（T+n）-S×i为第（T+n） -S×i个数据的实际值；t为所需要预测数据值的序号；n为训练集的个数；S为季节周期长度；T为（t-n）与S的余数。

（2）为避免MAPE值过小，并让更小的MAPE模型拥有更大的权重。将子模型MAPE值转变为倒数，再进行归一化处理后作为组合预测模型的权重值，计算公式为

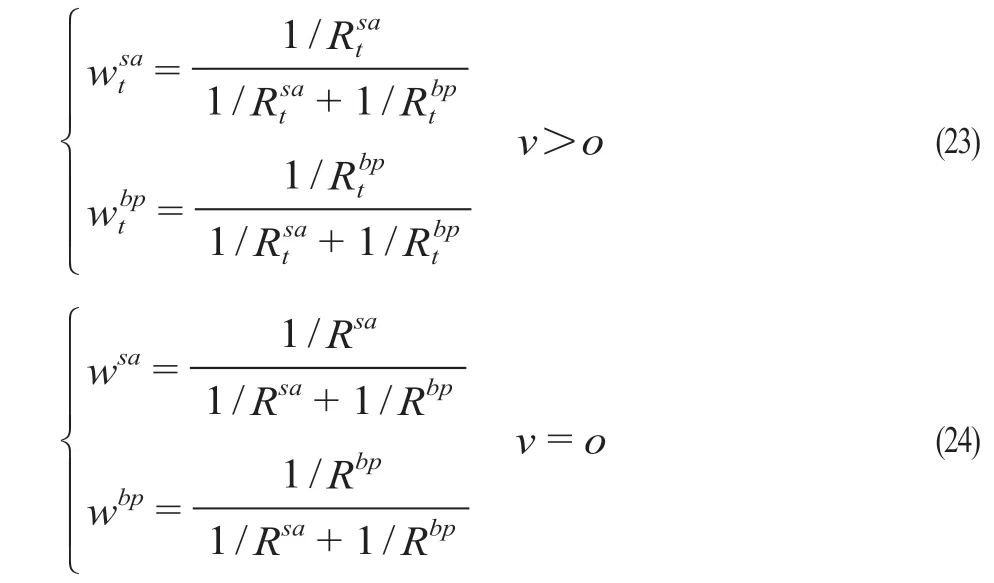
式中：wtsa为使用SARIMA模型预测第t个数据所对应归一化值；wtbp为使用GA-BP神经网络预测第t个数据所对应归一化值；wsa为当v= 0时使用SARIMA模型预测第t个数据所对应归一化值；wbp为当v= 0时使用GA-BP神经网络预测第t个数据所对应归一化值。

（3）结合权重值和子模型的预测值构建线性组合模型，计算公式为

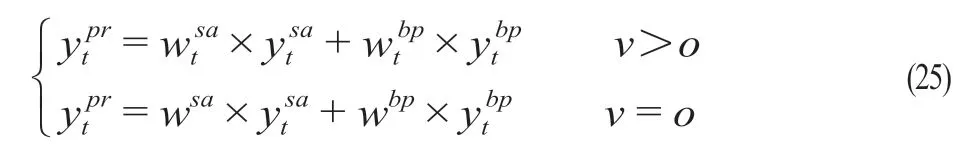
式中：ytpr为使用组合预测模型预测第t个时刻的预测值；ytsa为使用SARIMA模型预测第t个时刻的预测值；ytbp为使用GA-BP神经网络预测第t个时刻的预测值。

可以发现，研究构建的组合模型考虑季节性因素，实质上是对一个季节周期内每一个时刻都构建一个线性组合预测模型，权重均是以多个其他季节周期内对应时刻的百分误差为依据计算。

2 实例分析

2.1 案例数据来源

研究利用2020年7月1日—2020年9月20日（共82 d）哈尔滨南站进站客流数据标定模型参数，使用2020年9月21日—2020年9月30日（共10 d）哈尔滨南站进站客流量进行预测。

2.2 SARIMA模型预测

通过对数据进行1阶7步差分消除长期趋势和季节性周期影响，再依据差分后的自相关-偏自相关分析图反复尝试建立SARIMA （2，1，2）（1，1，3）7模型，自相关－偏自相关分析图如图2所示。模型的拟合优度R2值为0.79，SARIMA模型预测结果如表1所示。

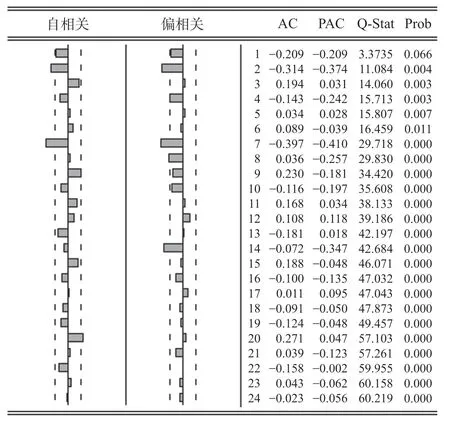
图2 自相关-偏自相关分析图Fig.2 Autocorrelation-partial autocorrelation analysis diagram

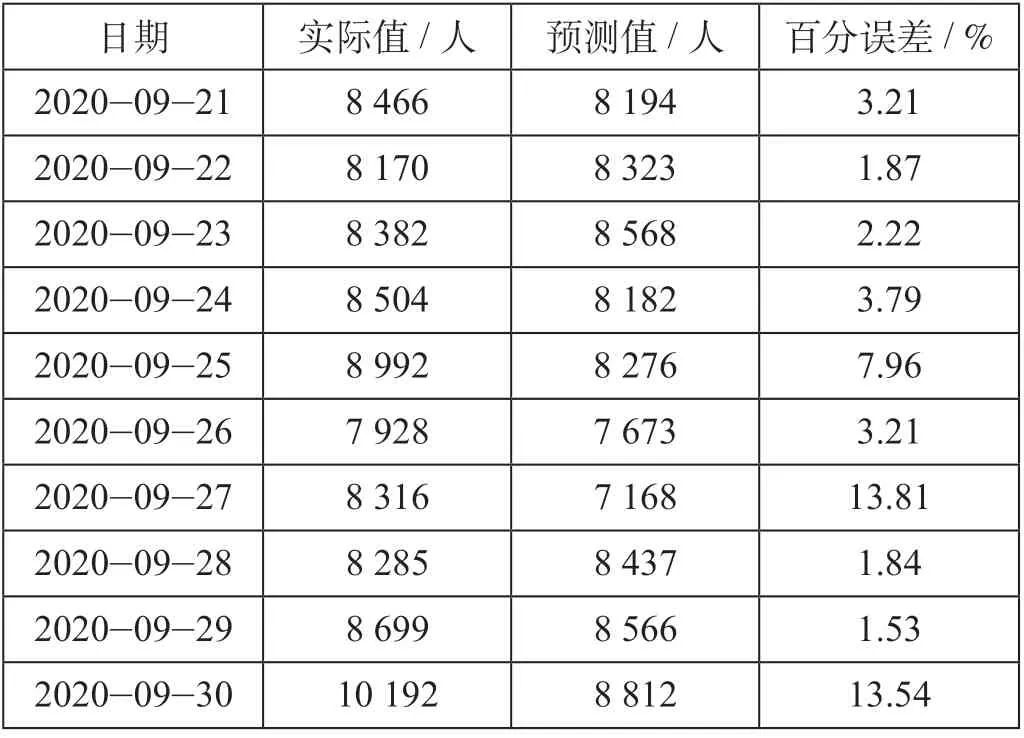
表1 SARIMA模型预测结果Tab.1 Prediction of SARIMA model

2.3 GA-BP神经网络预测

研究选取每日发车次数、是否工作日和周期数作为输入变量，并对训练集的输入变量和输出变量进行归一化处理，消除量纲不统一对模型的影响。

遗传算法的参数设定：总群规模为25，迭代500次，交叉概率为0.4，变异概率为0.2。

BP神经网络的参数设定：隐含层节点个数12个，训练次数为600次，学习速率为0.125，训练目标为0.000 05。GA-BP神经网络预测结果如表2所示。研究参考文献[19]使用校正后的拟合优度作为评判标准，其校正拟合优度R2值为0.65。

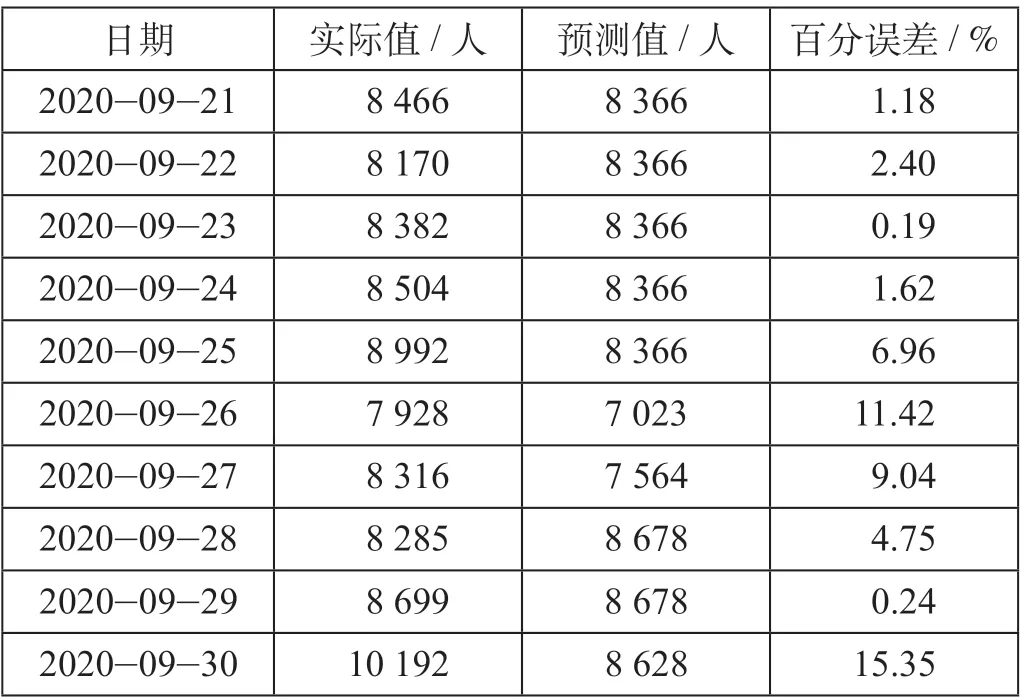
表2 GA-BP神经网络预测结果Tab.2 Prediction of GA-BP neural network

2.4 组合模型预测

首先利用拟合的SARIMA模型和GA-BP神经网络对训练集进行预测，考虑到SARIMA模型预测需要基于历史数据，因而只预测7月18日—9月20日共65 d的数据。接着计算2个子模型的MAPE，接着利用公式（19）—（24）计算8月31日—9月20日共21 d （v为3，S为7）每天的MAPE及其倒数。最后确定组合预测模型所对应子模型的权重值，并得出组合模型的拟合优度R2值为0.63，组合模型预测值如表3所示。

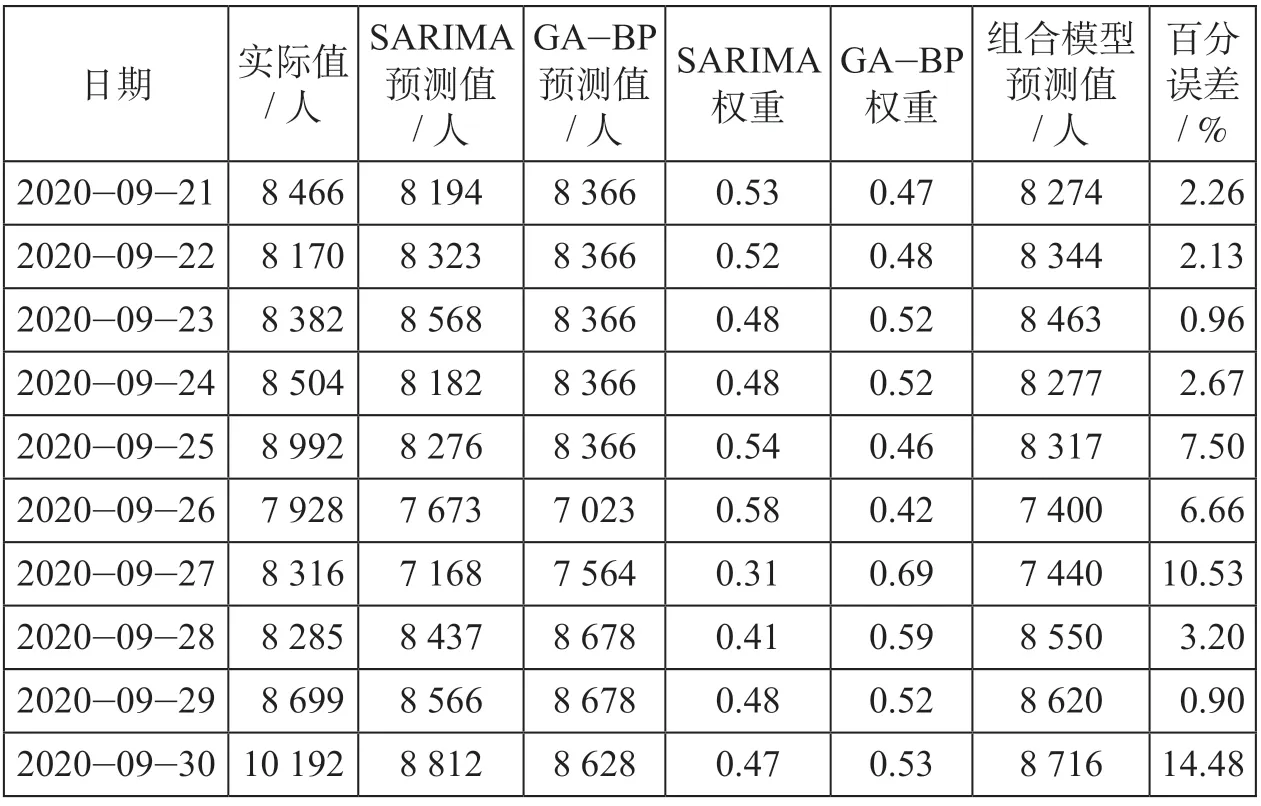
表3 组合模型预测值Tab.3 Predicted value of the combined model

参考文献[19]，研究设定拟合优度和校正拟合优度值不低于0.60时通过拟合优度检验。就R2值而言，SARIMA模型、GA-BP神经网络、组合模型均通过拟合优度检验。事实上，R2值大小不仅与预测结果相关，还与样本量的多少存在关系。本研究的训练样本为82个，SARIMA模型预测的训练样本为65个，GA-BP神经网络预测的训练样本为82个，组合模型预测的训练样本为44个，这样计算的R2值无法用于对比分析。为更好地对比分析各模型，选择组合模型对应的训练样本和实际客流值重新计算R2值，得出SARIMA模型为0.80，GA-BP神经网络为0.44，组合模型为0.63。可以发现，SARIMA模型对于地铁客流这类周期性的时间序列数据预测有着较为明显的优势；GA-BP神经网络在样本量较小时拟合优度远低于样本数为82个时的R2值，这表明模型的预测波动性较大；组合模型的拟合优度介于子模型间，能够避免单一模型样本量较少时拟合优度过低问题。

此外，为了更好地研究提出组合模型的效果，研究加入一个传统的线性组合预测模型（以下简称“组合模型0”）。该模型不同于组合模型根据一定规则挑选部分预测值的MAPE值作为其权重值的确定依据，组合模型0是以SARIMA模型和GA-BP神经网络所有预测值的百分误差之和作为其权重值确定依据，其计算公式为

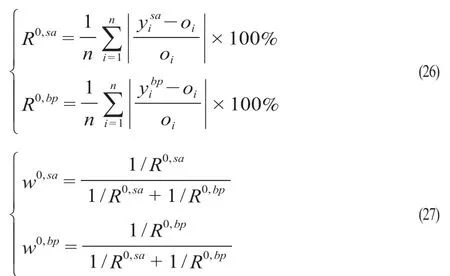
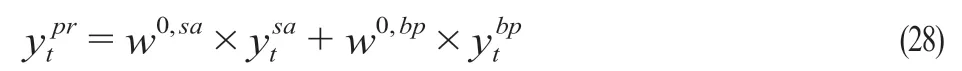
式中：R0,sa，R0,bp为SARIMA和GA-BP神经网络的MAPE值；w0,sa，w0,bp为组合模型0的SARIMA和GA-BP神经网络的权重值。

组合模型0的预测结果如表4所示。

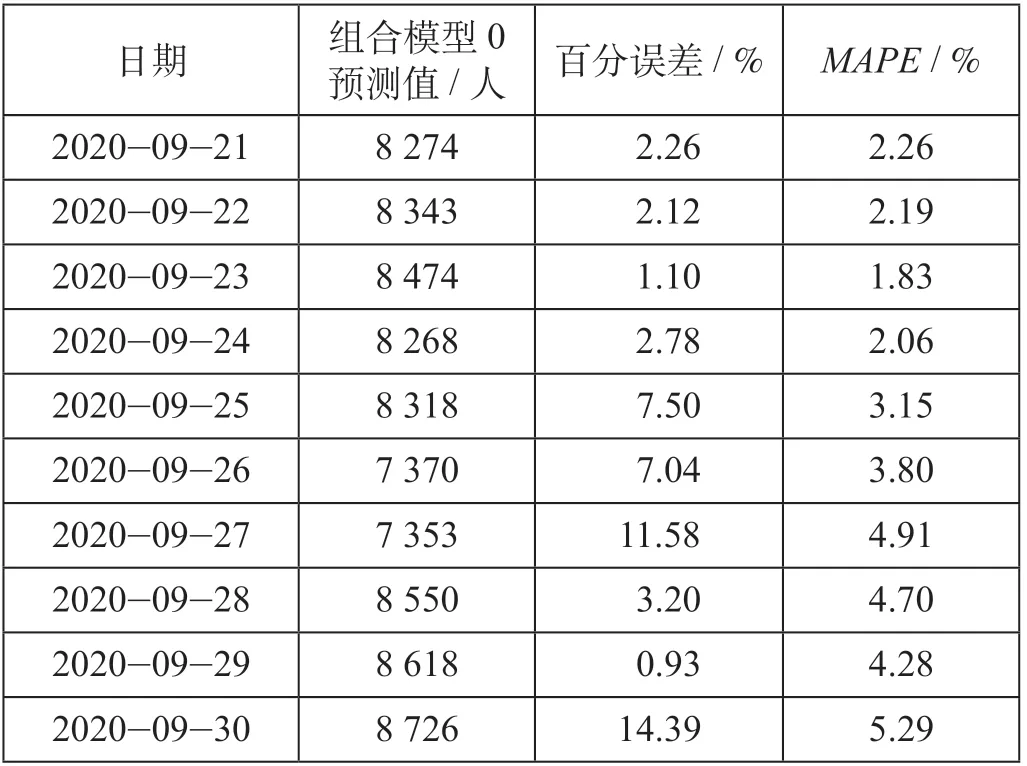
表 4 组合模型0的预测结果Tab.4 Prediction of combined model 0

2.5 模型结果分析

研究统计子模型与组合预测模型的百分误差并计算得出预测不同个数下的MAPE，各模型的百分误差和MAPE如表5所示，对应的百分误差和MAPE折线图如图3所示。

结合表5和图3可以发现，子模型的百分误差上下波动较大，组合模型介于两者之间，这表明组合模型有效缓解单一模型预测时出现波动较大的可能性。其中，组合预测模型的百分误差始终处于子模型之间，这表明组合预测模型的预测精度取决于子模型的预测精度，只有当所有子模型预测精度达到同一水平时组合预测模型的预测精度相对较高，组合预测模型并不能在子模型的基础上进一步提升其预测精度。通过对比组合模型0的百分误差可以发现，预测的10个数据中仅有2个预测值不如组合模型0，这表明研究提出的组合模型优于组合模型0。

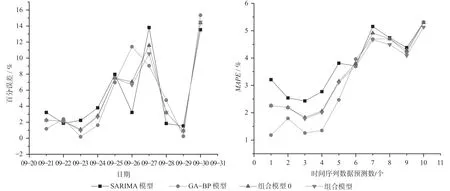
图3 百分误差和MAPE折线图Fig.3 Line charts of percentage error and MAPE

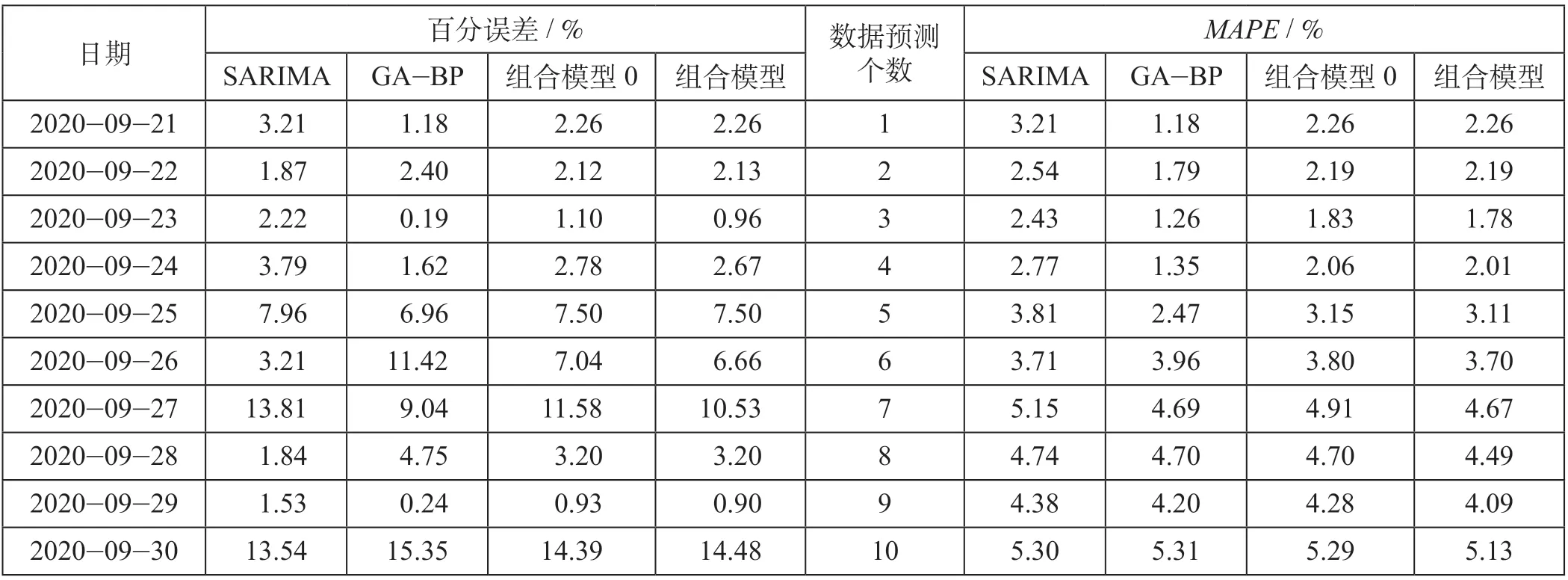
表5 各模型的百分误差和MAPETab.5 Percentage error and MAPE of varied models

通过观察各模型的MAPE、百分误差可以发现，MAPE值随着预测个数增加不断提高，但各模型MAPE值均不高于10%，且组合模型随着预测个数的增加，MAPE值增长速率越低，这表明组合模型长期预测效果较好。其中，SARIMA模型在短期预测（≤5 d）时预测精度较差，但是在长期预测（＞5 d）时均高于GA-BP神经网络；GA-BP神经网络在短期预测时预测精度高于SARIMA模型，但在长期预测时预测精度不如SARIMA模型；组合模型0无论在长期还是短期预测中，预测精度大体介于子模型之间；组合预测模型在短期预测中受限于预测个数过少缘故，预测精度一直介于子模型之间，但在长期预测时组合预测模型的预测精度好于所有子模型，当预测个数大于2个时，组合模型的预测精度高于组合模型0。