拱顶罐油气空间温度分布及其变化规律研究*

肖开喜 侯磊 赵智 李延豪 黄亚楠 张蕊

1中国石油大学（北京）机械与储运工程学院·油气管道输送安全国家工程实验室

2玉门油田分公司工程技术研究院

石油及其产品在储存和收发作业过程中，由于受到工艺技术和设备的限制，不可避免地会有部分轻质液态烃蒸发到罐内气体空间，通过呼吸阀逸入大气，造成无法预估的油品损失和环境污染[1-3]。早在20 世纪40 年代，国外相关机构和学者就开始对油品蒸发损耗理论进行研究，试图从理论上阐述油品蒸发的机理，探明影响蒸发损耗的因素和相关参数的变化规律[4-6]。与油品蒸发性质最为相关的参数是温度，对罐内温度分布及其变化规律的研究是油品蒸发损耗研究工作的重要组成部分。

杨宏伟等[7-10]实地测量了罐外环境温度、罐内油品温度和油罐气体空间不同位置的温度，对实测数据进行分析和处理，得到了气体空间温度分布规律。梁颖[11]在对某固定顶油罐温度分布实测数据进行分析的基础上，利用ANSYS 软件对温度场进行模拟，根据模拟数据拟合出气体温度分布公式，确定“小呼吸”起始与终了时的温度。VISSER 等[12]对液化气储罐内非稳态传热进行模拟，得到储罐内温度分布和到达液化气的热流密度，用温度分布和热流密度来预测储罐的蒸发损失，通过最小化蒸发损失优化储气罐的传热设计。张丽娜等[13]为研究呼吸阀冻结问题，建立了油罐气体空间温度分布二维稳态导热模型，采用有限差分方法将其差分格式化，运用列主元消去法求解方程，得到了气体空间温度分布规律。马晓宇等[14]根据实测数据建立了某固定顶油罐气体空间传热模型，对计算温度值进行分段线性拟合分析，为深入研究蒸发损耗提供了理论依据。

对油罐气体空间温度分布及其变化规律的研究主要有现场温度实测、专业软件模拟和数学模型计算三种方式，目前研究主要针对某一时刻的温度分布，对其变化规律的研究不够深入，对温度分布的影响因素处理较为简单。本文考虑地理环境、大气温度、太阳辐射和油品温度等影响因素，建立油罐气体空间二维传热数学模型；采用有限容积法对数学模型和边界条件进行离散处理，引入当量温度概念转化边界条件，简化模型求解过程；结合实际案例编写计算程序，对计算结果进行关联分析和误差分析，验证了模型具有很高的准确度。

1 数学模型

1.1 模型建立

油罐气体空间温度分布主要受到环境温度、太阳辐射和油面温度等因素的影响，罐内气体与环境和油品的热量交换是一个复杂的气-液-固三态传热过程，传热包括热传导、对流换热和辐射三种形式[15-16]。为方便建立数学模型，作以下假设：油罐为密闭空间不存在自然通风；油气内部只存在导热形式的传热；油气温度分布只是高度和半径的函数；罐顶和罐壁受到的太阳辐射分布均匀。气体空间温度变化的热量来源主要包括经罐顶、罐壁和油面传入的热流量，经罐顶、罐壁传入的热流量包括大气传入的热流量和油罐接收的辐射热流量，油面与气体的换热是以对流换热形式完成的。罐内气体空间换热结构原理如图1 所示。

图1 油罐热流图Fig.1 Heat flow diagram of oil tank

可将罐内气体空间视为圆柱形，忽略向阳或背阳对温度分布的影响，根据其对称性建立柱坐标下的二维稳态导热数学模型[17]。

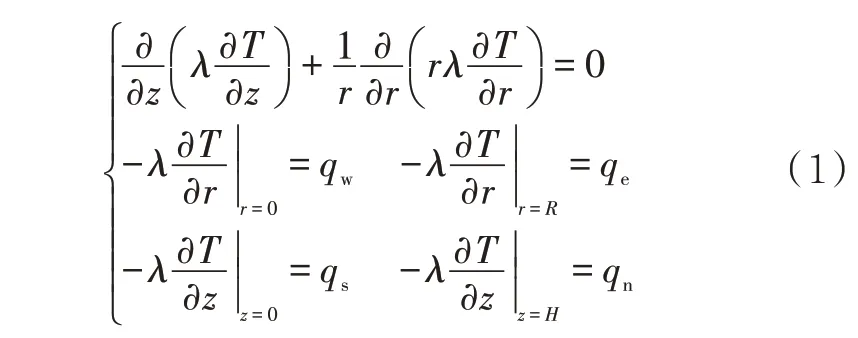
式中：λ为罐内气体导热热阻，w/（m·k）；qw为对称中心处传入的热流量，W/m2；qe为经罐壁传入的热流量，W/m2；Qe为罐壁辐射热流量，W/m2；Tf为环境温度，K；Te,b为罐壁处气体温度，K；re1、re2和re3分别为大气到油罐外壁传热热阻、油罐钢板导热热阻和油罐内壁到罐内气体传热热阻，m2·K/W；qs为经油面传入的热流量，W/m2；To为油品表面温度，K；Ts,b为油品表面处气体温度，K；rs1为油品表面到气体空间的传热热阻，m2·K/W；qn为经罐顶传入的热流量，W/m2；Qn为罐顶辐射热流量，W/m2；Tn,b为罐壁处气体温度，K；rn1、rn2和rn3分别为大气到罐顶外壁传热热阻、罐顶钢板导热热阻和罐顶内壁到罐内气体传热热阻，m2·k/W。

1.2 方程离散

有限容积法是求解温度场微分方程广泛使用的离散化方法之一，其基本思想是将计算域分成若干互不重叠的有限容积单元，使每一个网格结点都由一个有限容积单元所包围，这个有限容积单元在单位时间内接收或传出热量仅与其相邻的单元有关，并且等于相邻单元通过界面传入或传出热量的总和[18]。柱坐标下导热微分方程有限容积法离散如图2 所示。

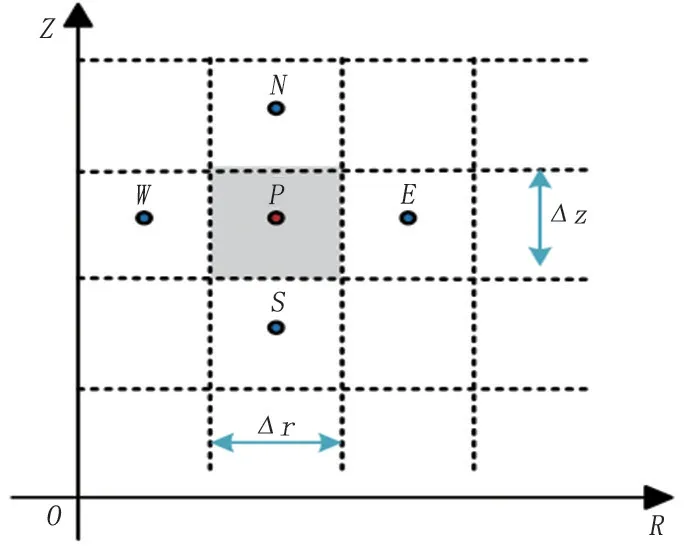
图2 柱坐标下有限容积示意图Fig.2 Schematic diagram of finite volume in cylindrical coordinates

采用有限容积法对二维稳态导热微分方程进行离散处理，离散后的形式如下

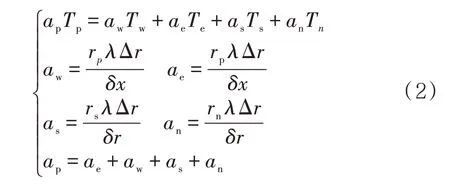
与某一边界相邻的内点，其对应系数值会发生变化，为了便于分析计算，将边界处内点系数值和边界条件同时考虑和处理。计算区域的边界为第三类边界条件，边界节点的温度未知，为了在Tp中不出现未知温度，需利用己知边界条件消去。

针对右边界处，式（2）可表示为

其中：ae(Te-Tp)=qerpΔz，qe为流进控制体的热流量。

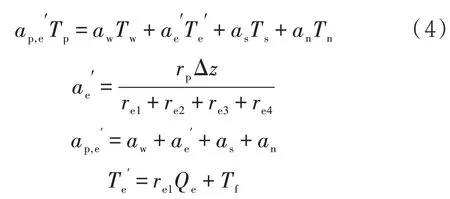
式中：re4为右边界控制体边缘到中心的导热热阻，m2·K/W；为同时考虑大气传入热流量和罐壁辐射热流量的当量温度，K。

通过引入当量温度概念将复杂的第三类边界条件转换成简单的第一类边界条件来求解微分方程。对左边界、下边界和上边界采取相同的处理方式，结果分别为

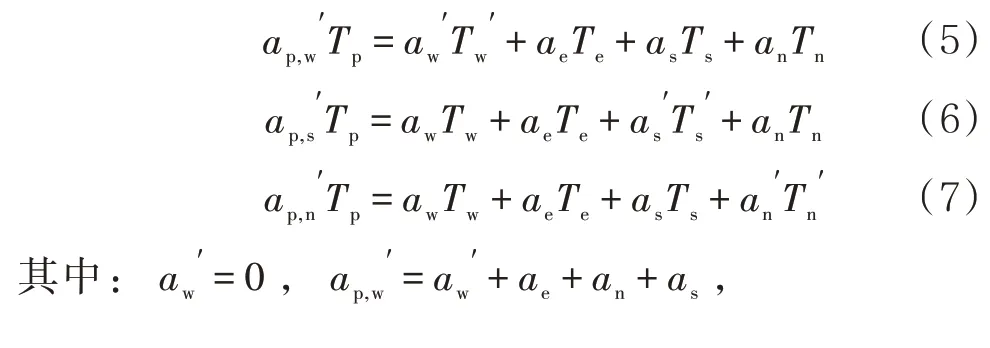
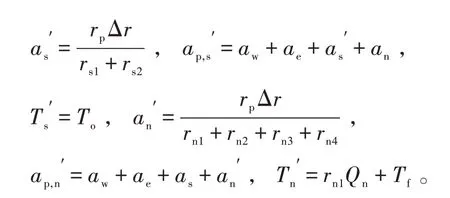
式中：rs2为下边界控制体边缘到中心的导热热阻，m2·K/W；rn4为上边界控制体边缘到中心的导热热阻，m2·K/W；为同时考虑大气传入热流量和罐顶辐射热流量的当量温度，K。

2 实例验证

某地区一座2 000 m3立式拱顶罐，直径D=14.57 m，罐体总高H=12 m，气体空间高度Hg=9.7 m。罐内气体导热系数λg=0.028 W/（m·K），油面对流换热系数h=11 W/（m·K），相关传热热阻re1=0.08 m2·K/W、re2=0.002 m2·K/W、re3=0.08 m2·K/W，rn1=0.1 m2·K/W、rn2=0.002 m2·K/W、rn3=0.1 m2·K/W。

以初夏某一天为例，查得正午太阳天顶角θ0=35°，测得部分时间的环境温度和油面温度如表1所示，根据已知参数即可求得油罐气体空间的温度分布及其变化规律。

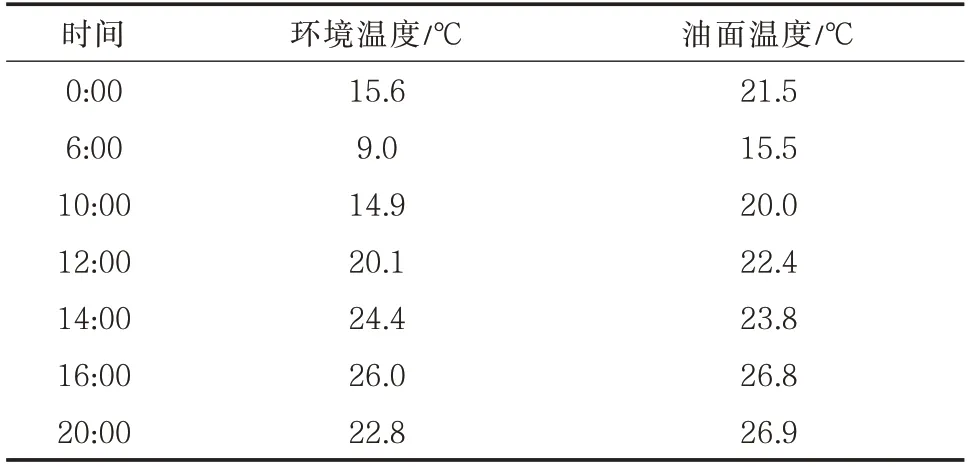
表1 部分环境温度和油面温度测量数据Tab.1 Partial measurement data of ambient temperature and oil level temperature

2.1 计算分析

罐顶或罐壁在不同时间、不同位置接收到的太阳辐射热流量不同，考虑大气对太阳辐射的削弱作用和罐顶、罐壁对辐射的吸收能力，与阳光照射方向垂直的单位面积罐顶、罐壁所吸收的辐射热流量用式（8）计算。

以正午太阳辐射强度计算，得到q0=420.05 W/m2。一天里阳光不能总是垂直照射在罐顶、罐壁上，根据兰贝特定律，任一时刻单位面积罐顶、罐壁所吸收的太阳辐射热流量可用式（9）计算。

式中：Qn、Qe分别为罐顶和罐壁单位面积吸收的辐射热流量，W/m2；圆频率ω=π/12；日出时间τrc=6。

计算得到一天内不同时间单位面积罐顶、罐壁所吸收的辐射热流量结果如图3 所示，根据环境温度和油品温度的一般变化规律，拟合得到一天内不同时间的温度。确定相关参数后，迭代计算罐内气体空间温度分布，分析其变化规律。Python 编程计算流程如图4 所示。

图3 罐顶、罐壁辐射热流量Fig.3 Radiant heat flow of tank top and wall

图4 温度分布计算流程Fig.4 Calculation process of temperature distribution

迭代计算得到不同时间气体空间各个节点的温度值，利用Python 软件强大的数据可视化功能对计算数据进行处理，能够更加直观地观测和分析温度分布情况。图5 为不同时刻罐内气体空间平均温度。由图5 可知：日出前气体空间的温度处于油面温度和大气温度之间；日出后由于太阳辐射热流量的传入，气体空间温度逐渐增加，很快就超过油面温度和环境温度，在午后2 h 左右达到最大值，之后温度又开始降低；日落后温度又处于油面温度和大气温度之间，这种状态一直持续到第二天日出。图6 为罐内气体空间不同高度的平均温度。由图6可知：日出前大气温度低于油面温度，气体温度随着高度的增加而减小；日出后到日落前大气温度高于油面温度，同时还有太阳辐射的作用，气体温度随着高度的增加而增加；日落时温度的递增趋势变为先增后减，之后这种变化趋势与日出前一样。

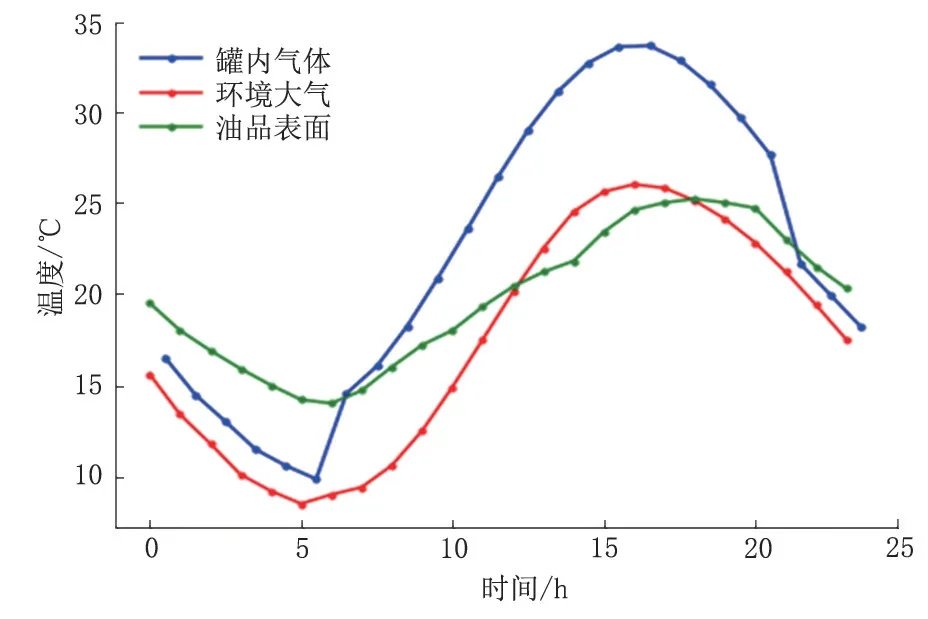
图5 气体空间、环境和油面平均温度Fig.5 Average temperature of gas space，environment and oil level

图6 气体空间不同高度平均温度Fig.6 Average temperature of gas space at different height

图7 为不同时刻油罐气体空间温度云图。日出前没有太阳辐射，气体空间温度分布受大气温度和油面温度影响，除油面附近一薄层外，同一高度气体空间温度基本相等，径向温差一般不超过1～2 ℃。日出时，只有罐壁接收到太阳辐射，罐壁附近不仅有大气传入的热流量，还有太阳辐射热流量，气体空间高温主要在罐壁附近，此时平均径向温差达到2.15 ℃。日出后，罐顶接收到的太阳辐射逐渐增大，罐壁接收到太阳辐射逐渐减小，在12:00 分别达到最大值和最小值，气体空间温度在纵向上出现明显的分层，正午过后罐壁接收到的太阳辐射逐渐增加，径向上又开始出现明显的温差。日落时，又只有罐壁接收到太阳辐射，此时气体空间出现明显的温度差，平均径向温差达到3.02 ℃，在气体空间中间位置的径向温差尤为明显。日落后，罐顶和罐壁都没有接收到太阳辐射，气体空间的温度只受油面温度和大气温度影响，罐内温度分布与日出前相同。

图7 不同时刻气体空间温度分布Fig.7 Gas space temperature distribution at different time

2.2 模型验证

通过对数值计算结果进行分析表明，建立的数学模型以及处理方式能够较准确地反映出油罐内部气体空间温度分布及其变化规律。图8 为气体空间不同高度的计算温度和测量温度对比图。由图8 可知，计算结果变化趋势与实测值一致，误差也较小。

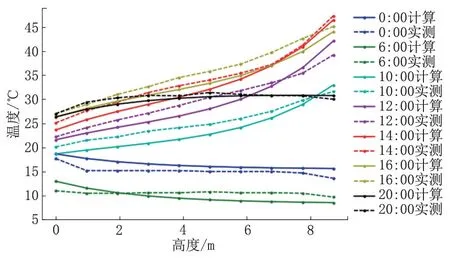
图8 不同高度的平均温度Fig.8 Average temperature at different height

为了进一步验证数学模型的可靠性，进行计算数据与实测数据灰色关联分析和误差分析。灰色关联分析为温度分布曲线趋势提供了量化的度量，误差分析用来量化判定计算数据的精确性，关联系数计算公式为[19-20]

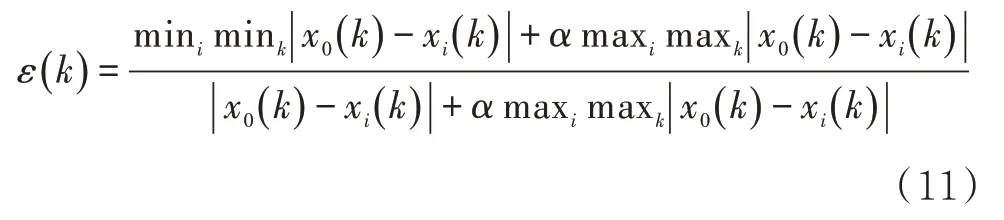
式中：x0(k)、xi(k)分别为不同高度位置对应的测量温度值和计算温度值；α为分辨系数，一般取0.5。

数值计算温度与实测温度的平均绝对关联度和平均绝对误差值如表2 所示。由表2 可知，所选取7 个时间段计算出的平均关联度均大于0.6，平均温度误差均小于2 ℃，计算温度与实测温度具有良好的关联性和较小的误差，能够充分反映油罐气体空间的温度分布情况。

表2 计算值与实测值的关联度和误差Tab.2 Correlation and error between calculated value and measured value

3 结论

（1）针对油罐气体空间与环境、油品之间的复杂气液固三态传热问题，综合考虑环境温度、油面温度和太阳辐射等影响因素，建立气体空间二维稳态传热数学模型，采用有限容积法对模型进行离散处理，引入当量温度概念转化边界条件，简化模型求解过程。

（2）根据某地区一座拱顶罐实测参数，利用Python 软件编程计算得到不同时间温度分布数值解，计算结果能够准确反映罐内气体空间的温度分布。为了进一步验证模型的准确度，用计算温度和实测温度进行误差分析和灰色关联分析，验证得到模型具有较高的准确性。

（3）从日出到日落，油罐气体空间为蓄热过程，热量经罐顶和罐壁传至气体空间，再传到油品使油品温度升高；从日落到第二天日出，气体空间为放热过程，热量经罐顶和罐壁传递给大气，同时油品温度也下降；罐内气体空间温度分布受太阳辐射影响最为明显，油气空间昼夜温差可比环境温差大10～20 ℃。

（4）温度分布直接影响到罐内压力和油气浓度，罐内压力决定呼吸开始和终了时间，油气浓度决定呼出气体中油气的含量。根据温度分布能够研究罐内压力变化和浓度分布，准确计算不同工况下油品蒸发损耗量，可为采取降低蒸发损耗措施提供指导依据。