基于MATLAB 人工神经网络的土壤腐蚀性评价模型*

朱庆杰 张建龙 陈艳华 雒振林 李雪 刘亚婷

1常州大学江苏省油气储运技术重点实验室

2华北理工大学建筑工程学院

3河北省建筑工程质量检测中心有限公司

近年来，国家强调建设清洁低碳、安全高效的现代能源体系，燃气作为一种经济、高效、清洁的能源被广泛应用。燃气管道运输量大、占地面积小、投资费用低，但长期埋在地下的燃气管道防腐材料不可避免的会受到土壤腐蚀而逐渐老化，安全性能逐年降低。埋地燃气管道的腐蚀破坏给各行各业带来了安全隐患，对经济、能源以及人身安全等诸多方面构成威胁，因此，对埋地燃气管道所处地的土壤腐蚀性进行科学评价、为管道的安全运行提供依据显得极其重要[1]。影响土壤腐蚀性的参数主要包括土壤电阻率、含水量、氧化还原电位、土壤pH 值、含盐量[2]。大多数评价方法是在数学模型的基础上对评价指标进行加权评判，如模糊综合法、主成分分析法等方法。虽然上述方法在实际应用中均取得了较好的效果，但依据操作人员和相关领域专家对评价指标法的权重进行赋值是不客观的，评价结果的准确性受主观因素影响很大，对于非线性问题的自学习、自适应的能力不足[3-4]。

人工神经网络（artificial neural network，ANN）在工业、金融等领域的预测和评价中被广泛应用，它能将诸多影响因素之间的共同作用通过非线性的方式计算出来，从而很好地解决这种非线性相关关系，是一种用于处理非线性问题的较好方法[5]。本文针对常州市埋地燃气管网所处的位置，确定了土壤的电阻率、含盐量、含水量、氧化还原电位、pH 值五个评价因子[6]。将神经网络理论应用到埋地燃气管网的风险评价中，构建影响因素评价因子和土壤腐蚀性概率大小之间的非线性关系模型，从而能够克服传统评价方法的一些缺点。通过对神经网络的结构的优化，最终建立基于MATLAB人工神经网络的评价模型[7]。

1 计算方法

人工神经网络模型采用级联的前向神经网络，这种网络的每一层都与输入层连接，拟合性能更好。神经网络各个网络层相互连接，信息由输入层依次向前传播[8]。其网络的一般数学表达式为

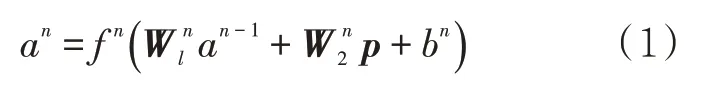
式中：a为每一层的输出向量；n为神经网络层数；f为激活函数；W为系数矩阵，每一层的神经元数目为行数，输入层的元件数为其列数；p为输入向量；b为阈值。

隐含层的激活函数为sigmoid 函数，输出层的激活函数为线性函数。求解神经网络每一层的权值、误差反向传播的算法偏值，误差反向传播是最小均方差（least mean square）算法的推广[9]。通过网络将敏感性反向传播的公式为

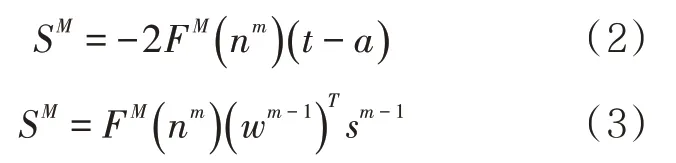
式中：SM为最后一层的敏感性；nm为权值和阈值的显式函数；F为近似均方误差。

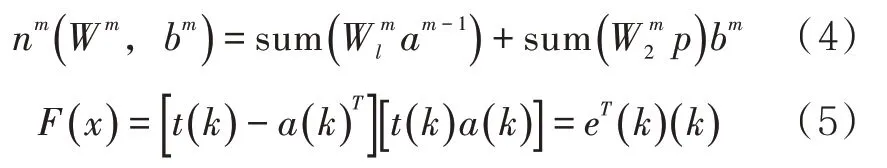
式中：a学习率；sm为剩余层的敏感性；t为实际的输出向量。

每次迭代用最速下降法修改权值和阈值的修改公式为

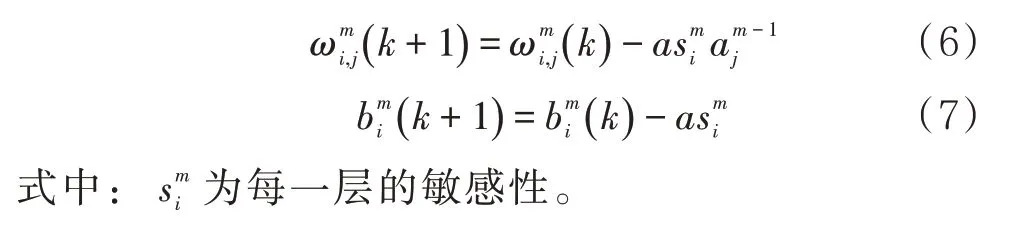
2 评价因子分析

从土壤腐蚀等级分类的指标出发（表1），将埋地天然气管道腐蚀的影响因素主要分为五类：土壤的电阻率、含水量、含盐量、氧化还原电位、pH 值。研究区块的管线图[10]如图1 所示。

表1 土壤腐蚀性等级分类指标Tab.1 Classification index of soil corrosiveness grade

图1 研究区块的管线图Fig.1 Pipeline diagram of the study block

（1）土壤电阻率是土壤腐蚀性等级中最重要的参数，体现了土壤的导电性能，甚至在一些情况下，土壤电阻率是决定性的因素。

土壤氧化还原电位体现了土壤氧化还原程度的强度。当电位高时，土壤体系通气性较好，氧化性强。反之则氧化性差，使管壁因失去电子而造成腐蚀。

土壤中的水分能够与可溶性盐组成电解液，产生腐蚀现象。当含水量超过临界含水量时，土壤腐蚀性的强度逐渐变弱；当含水量在临界含水量以内时，土壤的腐蚀性随着含水量的增加而变强。

土壤中的盐分是引起土壤导电性和电化学反应的又一重要因素，土壤中的含盐量和腐蚀性之间呈负相关的关系，土壤的腐蚀性随着含盐量的增大而降低。

土壤pH 值是土壤酸碱性强弱的指标，酸性土壤对管道的腐蚀性最强，中性、碱性较弱，可通过测定pH 值来判定土壤的腐蚀性。

通过对常州市土壤腐蚀性的计算，可知土壤电阻率、氧化还原电位、含水量、含盐量以及pH 值对腐蚀影响的权重依次为：0.261 5，0.063 4，0.033 3，0.129 0，0.512 8。则土壤腐蚀性的权重线性计算公式为

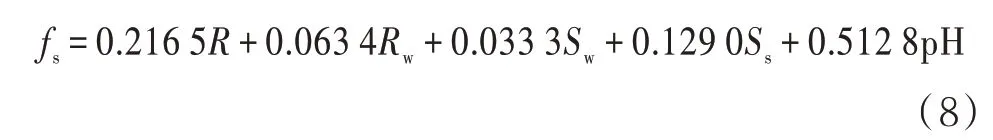
式中：fs为土壤腐蚀性；R为土壤电阻率；Rw为土壤氧化还原电位；Sw为含水率；Ss为含盐率；pH 为土壤酸碱度。

根据研究区块埋地燃气管网敷设的位置，选取具有代表性的500 组空间点作为评价的样本点，依次将土壤电阻率、氧化还原电位、含水量、含盐量和pH 值进行归一化处理，归一化后的部分数据如表2 所示。

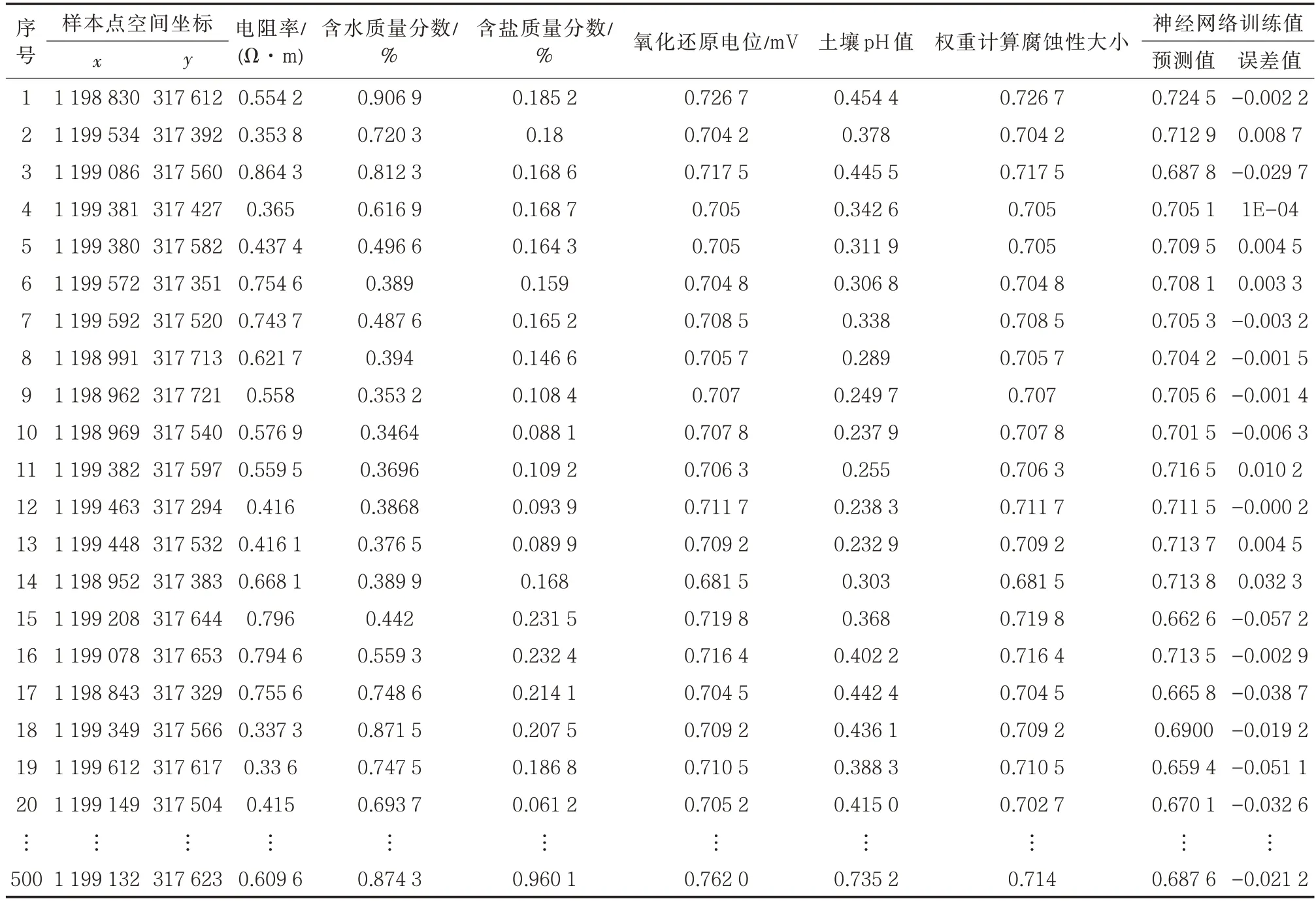
表2 样本归一化及计算数据Tab.2 Sample normalization and calculation data

3 人工神经网络评价模型

依据上文所述的计算方法，在MATLAB 软件中通过对训练函数的选取及隐含层结构优化，可以确定神经网络模型的网络结构，从而建立人工神经网络评价模型。

3.1 网络隐含层

级联前向神经网络的输入层元件为5，代表了5 种评价指标因子，输出层为1，代表土壤腐蚀性大小，设定训练步数为1 000，学习目标0.01，学习速率0.01，训练函数为莱文贝格－马夸特方法的BP 训练函数。隐含层的个数与网络训练误差如表3所示。

表3 网络训练误差Tab.3 Network training error

从表3 可以看出，在网络训练中隐含层为11，4 的网络，得到的训练误差值最小，逼近效果较好，并且经2 次就能够达到了训练目标误差。运用其他网络时的训练误差值较大，故最能接受隐含层结构为：2 个隐含层，隐含层1 和隐含层2 的神经元个数分别为11，4。

3.2 网络的选择

首先，选择莱文贝格－马夸特方法的BP 训练函数对网络进行训练，收敛速度快是其优点。当隐含层神经元数目为11，4，训练次数为2 次时，网络的误差为0.046 4。网络的训练结果见图2。

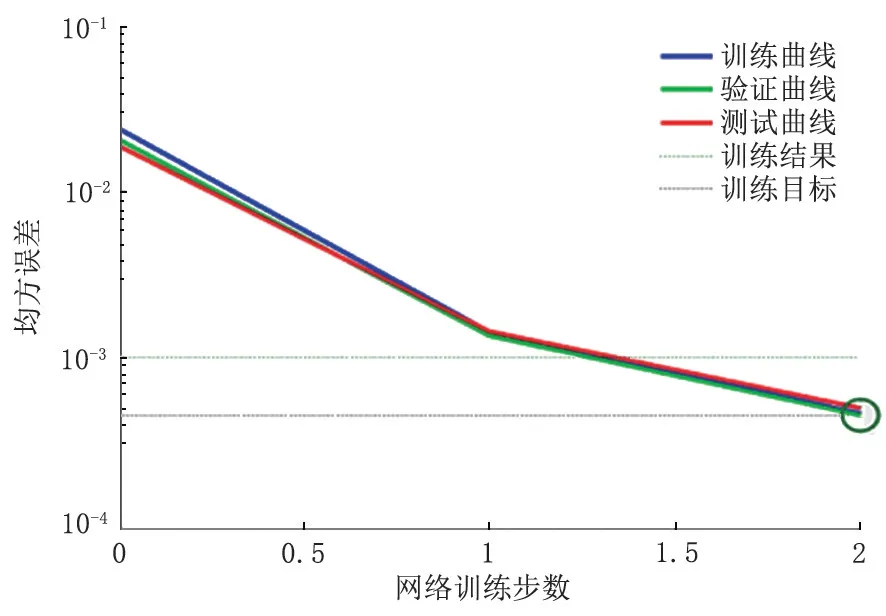
图2 莱文贝格－马夸特方法函数训练图Fig.2 Levenberg-Marquart algorithm function training graph

然后应用梯度下降和自适应的BP 训练函数进行网络训练，学习算法是梯度下降动量法，其学习速率是自适应的。网络的训练结果见图3，可见在训练步数为123 时，才达到训练误差的要求，这时的误差为0.213 3。

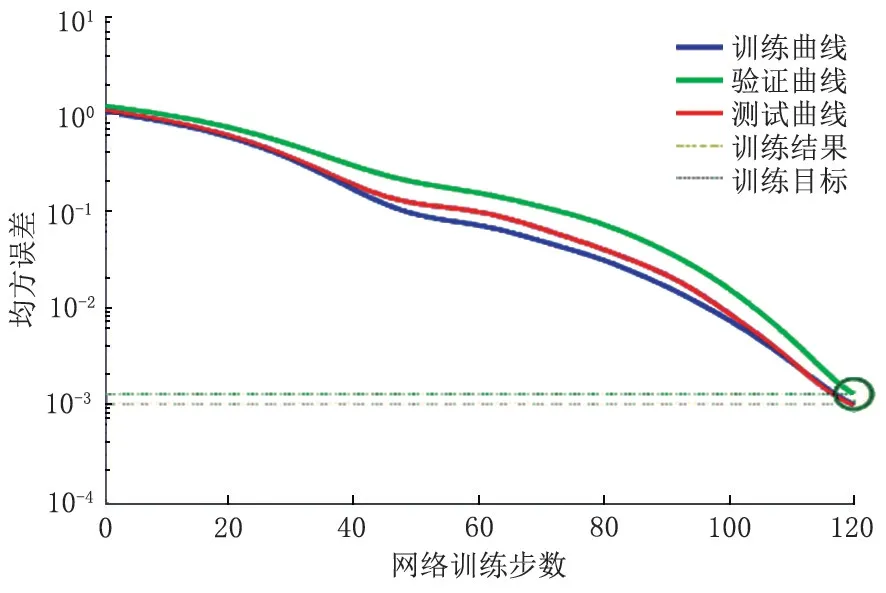
图3 梯度下降和自适应的BP 训练函数训练图Fig.3 Gradient descent and adaptive BP training function traning graph

最后是梯度下降的BP 训练函数对网络进行训练，此函数所用的学习算法是普通的梯度下方法。训练参数1 000 后，仍达不到误差要求。训练结果如图4 所示。不同训练函数的训练结果见表4。

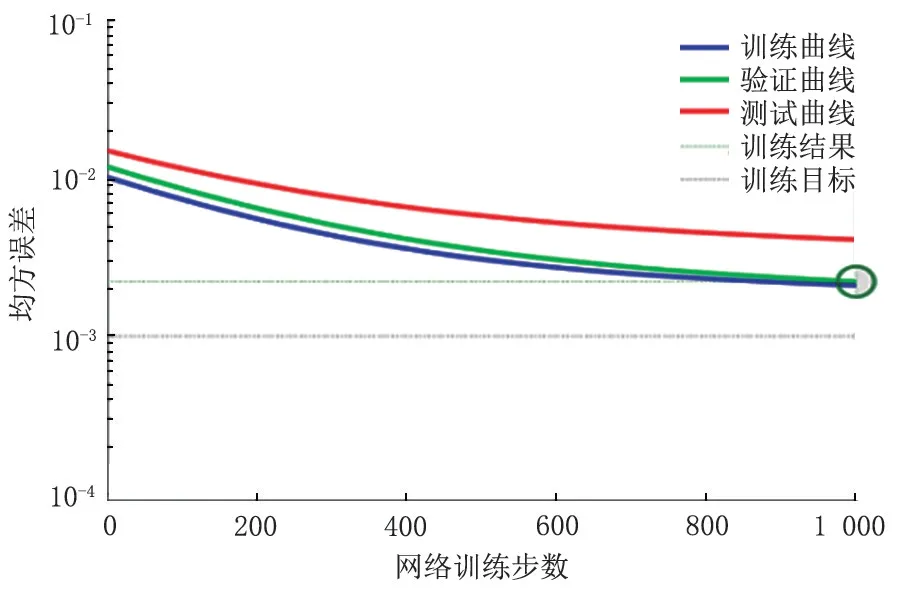
图4 梯度下降的BP 函数训练图Fig.4 Gradient descent BP function training graph

表4 训练函数对误差值的影响Tab.4 Influence of training function on error value

从表4 可以看出，不同的训练函数对网络的性能有着重大的影响，网络的训练误差、收敛速度都与选取的训练函数有密切的关系，所选取的训练函数既可能会使网络的误差达到要求、收敛速度很快，也可能使网络无法收敛。

3.3 最终网络结构

根据样本数据，通过网络的训练误差分析，确定了所采用人工神经网络模型的网络隐含层结构，根据训练函数的收敛性能以及训练误差，确定了最优的训练函数，最终采用的神经网络结构为元件数为11，4 的双隐含层、训练函数为莱文贝格－马夸特方法的网络。

神经网络模型的最终表达式为

式中：W10为第一隐含层到输入层的权值矩阵；W21为第二隐含层到第一隐含层的权值矩阵；W32为输出层到第二隐含层的权值矩阵；W20为第二隐含层带输入层的权值矩阵；W31表示输出层到第一隐含层的权值矩阵；W32为输出层到输入层的权值矩阵。xi（i=1，2，3，4，5）为输入层的元件数，也就是评价的指标。

这样就确定了常州市土壤腐蚀性评价的人工神经网络模型，根据任意空间位置土壤腐蚀性的各评价因子的调查结果，将这些评价因子的值带入已经建立的神经网络模型中，就可以得到常州市埋地燃气管网破坏危险性的评价结果。

4 结果分析

通过建立人工神经网络评价模型，依据燃气管道所在的空间位置和此位置各个评价因子的风险值，可以计算出这个位置土壤腐蚀性的大小。依据表2 的计算结果，结合图1 所示的研究区块的管线图，得到土壤腐蚀性较小的区域分布在管线图的中部地区，这里洪水集中的较少、土壤含水率较低、土壤电阻率较大，因而土壤腐蚀性较小，适合铺设埋地燃气管道。根据燃气管网的布置图也可以看出，此处埋地管道布置紧密，其他区域的腐蚀性较大，管道的铺设松散，也尽量避开险区。此方法得出的土壤腐蚀性评价结果人为主观性因素不明显，能更好地反应研究区块实际的土壤腐蚀性特征。

人工神经网络模型可以对非线性相关的各评价指标做出较为准确的预测。从表3 可以看出，网络的训练误差不仅与隐含层的层数有关，还与隐含层的元件数目有关。当隐含层层数及元件数目增加时，网络的训练步数也增加。从图2、图3、图4 以及表4 可以得出，神经网络的训练函数对网络性能和误差也有着重大影响。本例中，采用莱文贝格－马夸特方法BP 训练函数训练网络时，收敛的速度较快，仅训练2 步后就达到了误差要求，误差最小值为0.046 4；采用梯度下降和自适应的BP 训练函数训练网络时，虽然可以达到设定的误差要求，但是收敛速度较慢；采用梯度下降的BP 训练函数训练网络时，经过1 000 次后迭代失败，没有达到精度要求。

5 结论

本文应用人工神经网络的方法建立了常州市土壤腐蚀性的多元非线性模型，得到了研究区块的埋地燃气管道在土壤腐蚀性下的破坏风险分布，同时得出如下结论：

（1）由于埋地燃气管道土壤腐蚀性大小受到多种影响因素的共同作用，难以精确预测其危险性，但是如果能够找到影响因素和土壤腐蚀性之间的某种非线性的关联关系，就可以建立非线性结构模型，对其腐蚀性的概率大小进行预测。人工神经网络是解决这种非线性相关关系、建立非线性模型的好方法。

（2）依据最终构建的土壤腐蚀性评价模型以及埋地燃气管道所在的空间位置坐标点，能够得出埋地管道在该区域的土壤腐蚀性概率的大小。在敷设管道的时候，应最大限度地避开这些腐蚀性较大的危险地带，从而可以做好埋地燃气管道的安全防护。在腐蚀性较小的区域，敷设的管道不易受到土壤腐蚀。

（3）构建人工神经网络模型主要是对神经网络模型的选择、对网络结构的确定，以及对神经网络隐含层层数、隐含层的元件数确定。另外，人工神经网络采用不同的训练函数，对网络训练误差值均有较大的影响。因此，网络结构的优化分析，是建立人工神经网络模型的关键。