基于残差网络的微波关联成像目标重构方法
2021-12-22李海龙赵露涵
李海龙, 苗 强, 赵露涵
(空军工程大学信息与导航学院,西安,710077)
目前成像雷达主要有实孔径雷达、合成孔径雷达(synthetic aperture radar)、逆合成孔径雷达(inverse synthetic aperture radar)[1-3]。实孔径雷达距离向分辨率取决于发射信号的带宽,方位向分辨率受限于天线或阵列孔径的大小,想要提升分辨率只能通过增大天线孔径或提高发射信号带宽,这将导致雷达体积和重量的增加,影响实用性。合成孔径雷达和逆合成孔径雷达都依赖距离-多普勒效应,需要雷达与观测目标存在相对运动,只能进行侧视或斜视成像,无法凝视成像。自A.Gatti等[4-5]研究人员实验证实了经典热光源也可以实现关联成像,将量子强度关联成像思想拓展到微波领域,衍生出了微波关联成像[6],为解决传统雷达所受限制提供了新的思路和方向。
然而,现有的微波关联成像重构算法如伪逆算法(pseudo-inverse algorithm)、截断奇异值分解(TSVD)算法[7]、Tikhonov正则化算法等不仅要求高采样率,其重构结果也不够理想。E. J. Candes、J. Romberg、T. Tao 和D. L. Donoho等[8]提出的压缩感知(Compressed sensing)理论利用自然物体的稀疏性,可以极大地减少重构所需要的采样次数,在低采样次数下,反演出目标图像。压缩感知理论也衍生出了许多重构算法,但均面临着计算复杂度高,反演时间长等问题。阻碍了微波关联成像的发展。
近年来,随着计算速度的迅速提升和数据量的急剧增加,深度学习已经广泛应用于图像处理和计算机视觉领域。许多研究人员也尝试将深度学习应用于关联成像目标重构中,2017年,SINHA等[9]实验证明了通过训练后的深度神经网络可解决计算成像问题。2018年,HE Y等[10]将卷积神经网络应用于鬼成像,该方法成像速度有所提升,但成像效果较差,模型泛化能力较差。2019年,中国科学院上海光学精密机械研究所司徒国海课题组[11]提出了一种利用仿真数据训练神经网络用于恢复实验数据的方法,解决了训练数据及难以获得的问题,并在计算鬼成像中验证了该方法的可行性。为深度学习在关联成像方面的应用提供了理论基础。LIU等[12]提出基于卷积神经网络的压缩感知重构算法,将压缩感知测量值作为网络的输入进行图像重构,可以实现在低采样率下的目标重构,但该方法没有利用到采样矩阵的信息,使得图像部分信息丢失,造成重构效果不理想。
本文借助卷积神经网络(convolutional neural network,CNN)与残差网络(residual network,ResNets)[13]特征提取优势,提出一种基于残差网络微波关联成像目标重构方法,以接收到的回波数据作为网络的输入,进行初期重构后通过训练好的特征提取网络和图像增强网络,可以得到高质量反演图像。
1 相关理论
1.1 微波关联成像基本原理
微波关联成像基本原理见图1,其物理过程可以简单描述为以下几步:首先,将待成像区域均匀划分成n个大小相等的网格,每个网格的散射特性用其中心点的后向散射系数σ(i)代替,利用相控阵天线构造时空二维随机辐射场Ei(t,r),辐射场与待成像目标相互作用形成散射场Fi(t,r),雷达接收器接收散射回波Fi,将接收到的回波Fi与二维随机辐射场Ei(t,r)做关联处理反演出图像信息。

图1 微波关联成像模型
辐射场是由阵列天线发出的电磁波经空间传播后生成,是各个阵元的发射信号在某同一位置的叠加,如式(1)所示:
Ei(t,r)=
(1)
式中:f(t)为天线发射信号;S(ri,r)表示天线发射阵列中第i个发射阵元的天线方向图;ri表示第i个发射阵元到待成像目标的距离;G(r,ri,t,t′)相关性格林函数,表示散射场和辐射场的关系。
散射场是由辐射场与待成像目标相互作用形成的,是某同一位置各个网格散射信息的叠加。雷达散射回波是由散射场经空间传播得到,见式(2):
(2)
式中:r0表示接收阵元的位置;G(r,ri,t,t′)取标量形式。
在不考虑噪声的情况下,回波信号可以表达为一列关于时间的采样序列。成像区域被分割成n个具有相同尺寸的离散单元,将其展开成列向量与每个点对应的辐射场做乘法,则雷达散射回波Fi(t)的表达式可简化为:
(3)
简化表示为:
F=E•σ
(4)
可以看出,式(3)中的每一行都是一个方程,表示待成像区域被划分成n个离散单元后,在ti时刻,接收回波等于每个网格的辐射场与其后向散射系数的乘积。微波关联成像的反演本质就是利用式(1)对式(3)中每个方程进行求解,求解出目标后向散射系数σ,得到目标的反演图像。
1.2 卷积神经网络与残差网络
近年来,卷积神经网络被证明具有强大的特征提取能力,在图像处理领域应用十分广泛,其工作原理主要分为网络模型的定义、网络训练以及网络预测。典型的卷积神经网络一般由输入层、卷积层、池化层、全连接层、输出层组成[14]。可根据不同的应用场景对卷积神经网络模型结构进行设计。训练数据集也是影响神经网络模型性能的主要因素,不同的训练数据集训练出的神经网络模型性能往往差距很大,根据实际需求选取适当的训练数据集。随着网络越来越深,训练变得原来越难,网络的优化变得越来越难。残差网络通过加入残差块(residual block),使神经网络模型变得更加容易被优化。两种不同的残差块结构如图2所示。
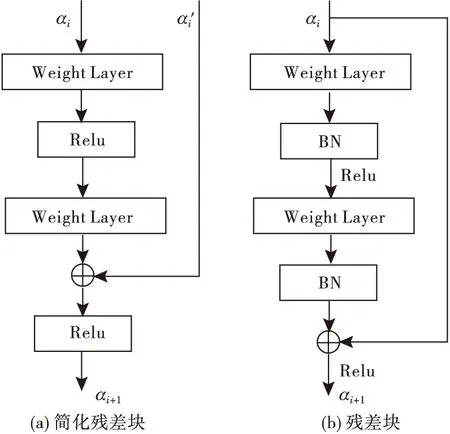
图2 2种不同残差块结构
2 基于残差网络的重构模型设计
模型由3个部分构成:初期重构网络,特征提取网络和图像增强网络。具体过程简单描述为:选取图像中亮度分量作为被测目标后向散射系数,利用相控阵天线分配随机相位方法[15]模拟生成时空二维随机辐射场,辐射场与散射系数相互作用得到散射场,雷达接收机接收散射回波,将散射回波采样序列作为初期重构网络的输入,进行直接关联重构得到初期重构图像,此时图像中含有被测物体信息,但视觉效果较差难以分辨。因此使用特征提取网络对初期重构图像进行特征提取并进行重构,可以得到比较模糊但含有被测物体特征的中间重构图像,将其作为图像增强网络的输入,图像增强网络对其进行特征增强和噪声去除,即可输出重构后优质的被测物体图像。具体细节见图3。

图3 基于残差网络重构模型
2.1 初期重构网络
传统重构算法要求采样数至少等于待成像区域所划分的网格数,才可以实现对目标的重构,这样就要求接收机的采样频率很高,十分影响实用性。初期重构网络以雷达接收机接收的散射回波采样序列作为网络输入,进行直接关联计算输出初期重构图像。可根据不同的采样率要求,取不同的序列长度。将采样序列与时空二维随机辐射场进行关联计算得到初期重构图像,有效降低了图像重构的采样数量。
2.2 特征提取网络
低采样数的雷达序列经初期重构网络重构得到的图像十分模糊,特征提取网络的主要是从初期重构图像中提取被测物体的特征信息并进行图像重构。因此,其输入是一张尺寸为28×28×3的初期重构图像,经过32个大小3×3的卷积层对输入图像进行高维特征提取,将提取到的高维特征信息分别经过8次如图所示的残差块(ResBlock)和32个大小3×3为的卷积核后与高维特征信息进行加权计算,最后一层选用3个大小1×1为的卷积核,步长为1,不设置激活函数,进行通道调整和非线性映射。输出一张尺寸为28×28×3的含有被测物体特征的中间重构图像。具体参见图4。
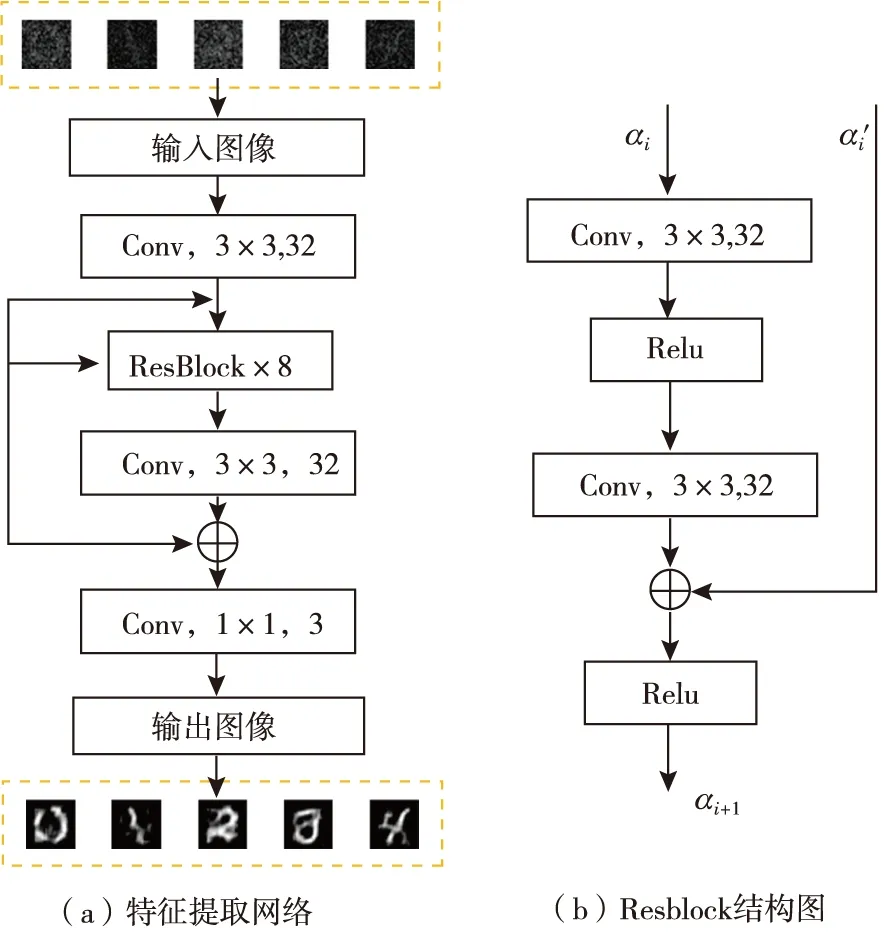
图4 特征提取网络
2.3 图像增强网络
特征提取网络输出的中间重构图像虽然特征明显但含有大量噪声,特征信息不够清楚。因此加入图像增强网络可以实现对噪声的有效去除,同时还能增强图像特征,提升重构质量,参见图5。

图5 图像增强网络
由图5可看出,图像增强网络由3个卷积层构成,其输入为一张尺寸为28×28×3的中间重构图像,前两层都采用大小为3×3的卷积核,步长为1,激活函数选择Relu,分别生成32个和8个特征图;第3层选择3个大小为1×1的卷积核,步长为1,不设置激活函数,进行通道调整。输出为一张尺寸为28×28×3的优质重构图像。
3 仿真实验与结果分析
3.1 仿真实验
为了评估本文所提出的重构算法,进行仿真实验,首先基于matlab2016b利用相控阵天线构造时空二维随机辐射场,工作波长设置为0.008 2 m,目标中心与发射天线距离为2 m。基于Tensorflow 2.2平台对上述神经网络模型进行搭建。选取2组数据集分别进行仿真,一组数从MNIST手写数据集[16]中随机选取一组(包含20 000个大小为28×28的训练图片和10个28×28测试图片)训练图像,记为数据集A。另外一组选取STL-10数据集中BSDS200中199张大小为481×321的图片,并从BSDS500_test中选择3张作为测试图片,对其进行灰度图像转换并按照MNIST手写数据集的尺寸对其进行均匀切割剪裁处理,可以得到37 213张大小为28×28的图像,记为数据集B。分别将2组数据集进行归一化后输入初期重构网络,取采样序列长度为78,进行初期重构得到初期重构数据集A′和数据集B′。
将数据集A′和数据集B′分别与数据集A和数据集B进行对应,对特征提取网络进行训练。两次仿真实验均训练30个周期,每个周期内分别含有16个批次和581个批次,每个批次含有64张大小为28×28的图片。采样均方误差(MEAN)作为损失函数,优化算法选择自适应矩阵估计(adaptive matrix estimation)优化算法,学习率设置为0.001。训练结束后,分别输入数据集A′和数据集B′得到中间重构数据集A″和数据集B″。将数据集A″和数据集B″分别与数据集A和数据集B进行对应,对图像增强网络进行训练,训练100个周期。其他参数与上述相同。训练结束后输入测试图片,就可以重构出目标图像。
3.2 仿真结果分析
本节将本文算法分别与伪逆算法和压缩感知算法进行比较。其中压缩感知反演算法选择正交匹配追踪算法(orthogonal matching pursuit)[17],迭代次数设置为15。本实验选用MNIST手写数据集测试集中的10张图片和BSDS500_test中的3张标准测试图片进行重构测试。分别在0.05、0.1、0.25的采样率β下进行无噪声重构测试,MNIST database仿真结果见图6。

图6 MNIST database不同采样率下的3种方法实验结果对比
MNIST database数据集仿真实验结果表明,采样率对重构效果的影响十分明显,随着采样率的提升,重构也效果越来越好。虽然MNIST database数据集图片稀疏度较高,但在采样率比较低的情况下压缩感知和伪逆算法重构出的图像模糊不清,含有大量噪声,难以分辨图像。本文算法重构出的图像相对于其他两种重构方法,在对比度和边缘特征都有显著增强,对背景噪声也有滤除作用,重构图像的视觉效果优于其他算法。
BSD500 database仿真结果如图7,BSD500 database相比于MNIST database数据集中的图像特性更加丰富。仿真结果表明,在低采样率下,伪逆算法重构图像含有大量噪声,特征信息模糊,视觉效果不佳,甚至无法成像。压缩感知对图像的特征信息有所保留,但仍含有大量噪声,图像模糊。本文算法相比于其他算法无论在以上两个方面都有所提升。为进一步客观评价本文方法的优越性,进行峰值信噪比(peak signal to noise ratio,PSNR)[18]和图像重构时间对比分析。2组数据集上的平均PSNR值如表1所示,图像重构时间对比分析如表2所示。

图7 BSD500 database不同采样率下的3种方法实验结果对比
表1表明,本文算法重构图像的平均PSNR值高于伪逆算法和压缩感知算法,在相对较低的采样率下,伪逆算法和压缩感知算法重构的图像含有大量噪声,图像特征信息不明显,与原图相似度较低。通过本文算法可以有效避免这些问题。

表1 不同采样率下图像重构平均PSNR
表2为单张测试图片在不同采样率下各算法重建图像所需要的平均运行时间。可以看出,在不同的低采样率下,本文方法重构时间已达到0.061 s左右,小于压缩感知方法重构时间。因此相比于传统微波关联成像重构方法,本文重构方法在保证重构图像质量的前提下,所需重构时间更短。

表2 单张测试图像在不同采样率下各算法重建图像的平均运行时间 单位:s
4 结语
本文将残差网络和卷积神经网络应用到微波关联重构算法中,提出一种基于残差网络的微波关联图像重构方法,利用残差网络的特征提取优势,可以有效解决微波关联传统重构算法在低采样率下重构图像成像质量差问题。为验证本文算法的有效性,分别与伪逆算法和压缩感知算法进行了实验仿真分析对比得到:在相同采样率下,本文算法能够重构出更优质图像,并且拥有更高的PSNR值;在高采样率下,本文算法提供了更优的重构质量,保留了更丰富的图像信息;在低采样率下,也能保留图像的关键信息。同时,本文方法为解决微波关联成像速度问题提供了一个新的解决方案,有效推动了深度学习在雷达微波关联成像领域的应用。在后续的研究中,将进一步完善网络模型的结构提升模型的泛化能力。
