思维接力：小初衔接的应然视角

陆椿

【摘 要】当前，同属于基础教育阶段的小学、初中两个阶段，在数学课程学习中各自为营的现象比较普遍。本文从义务教育一体化的视角出发，以“数的运算”为例，从沟通思维的联系、感悟思维的递进、体会思维的延展等方面阐述了小初衔接的关键是做好思维衔接。

【关键词】数学思维 小初衔接 数的运算

分析小初数学教学的衔接问题，笔者以为，首要是关注并解决好思维衔接的问题。以“数的运算”为例，初中阶段的内容较之于小学有两大显著变化：一是数的范围扩充到有理数领域，数的运算也相应地在加、减、乘、除四则运算的基础上引入了乘方、开方运算，实现了由局部到全局的跨越。二是研究领域从“数”扩充到“式”，从算术运算向代数运算过渡，这是学生在认知上由具体到抽象、由特殊到一般的跨越。

一、类比：沟通思维的联系

无论是小学还是初中，基本算理是一脉相承的。教学中应关注知识整体，沟通不同单元板块之间的内在联系，并做适当延伸。在“数的运算”的复习中，出示如下题组：

①345+2955=3300 ②18.6+7.88=26.48

③3— 4-1— 6=9— 12-2— 12=7— 12

上述由整数、小数和分数三个计算组成的题组，学生在计算得到正确结果方面显然不存在困难。重点引导学生以此来分别复习整数、小数、分数加（减）法的计算法则。这三种运算表面上看有比较大的差异：整数加（减）法要求相同数位对齐;小数加（减）法要求小数点对齐;而分数加（减）法关键是要统一分数单位。继续引导学生从表面走向深入：实质上三则计算法则的核心都是相同计数单位方可直接相加减，异分母分数之所以不能直接相加减是因为它们的分数单位不统一，需要转异为同。在学生初步感悟到“数的加减运算，就是‘基本单位’相同情况下，‘基本单位’的个数的加减运算”的基础上，拓展思维，如：4a+5a，“基本单位”是a，就是4个a加5个a等于9个a，即9a;6ab-2ab，“基本单位”是ab，就是6个ab减2个ab等于4个ab，即4ab。如此尝试用“基本单位”的思维方法来进行含有字母的式子的加减运算，学生进入初中后，通过类比便能更快地掌握和理解式的运算。

在小学阶段的教学中，还有很多地方可进行上述类比，本文就不一一列举。小学阶段的计算教学，大多通过生活情境引入。如整数的四则混合运算，就是通过模拟购物，先分步再综合，最后得出运算顺序。这样的编排，符合小学生的年龄特征，也利于学生通过现实情境来理解先乘除再加减的运算顺序。进入初中后，引入了乘方和开方运算，由二级运算拓展到三级运算。因此在教学中，可结合情境向学生说明：从运算的发展来看，加减法是最基本的运算，乘法是相同加数连加的简便运算，除法则是递减相同减数的简便运算（也是乘法的逆运算），乘除法比加减法高一级。因此，“先乘除再加减”既是解决实际问题的需要，也是根据数学的发展而规定的。而乘方（开方）则是第三级运算，乘方可以看作是乘法的简便运算，要优先计算，这是由法则本身的形成及法则之间的关系规定的。这样就便于学生循序渐进地理解和掌握三级运算的运算顺序。

教学中还要注意沟通四则运算的意义、算理和算法、运算律和运算性质之间的联系。理解运算律（特别是乘法分配律）和运算性质的本质和作用，沟通一级运算和二级运算之间的联系。沟通“数”与“式”的联系，通过类比将“数的运算”过渡到“式的运算”。挖掘教材中的衔接点，如乘方、解方程、面积和体积的公式计算等，主动实现小初的整体衔接。

二、迁移：感悟思维的递进

从“数”到“式”的变化，是初中阶段显著的一个变化。用字母表示数是小初衔接的一项重要内容，是初中阶段学习代数式、整式的基础。如：儿子今年a岁，爸爸的年龄是儿子的4倍，妈妈比儿子大26岁，则爸爸年龄为4a岁，妈妈年龄为（a+26）岁。这些关系，在小学称为用字母表示数，而到了初中，4a我们称为单项式，a+26为代数式。小学阶段可适当加强用字母表示稍复杂的数量关系的教学，以顺利过渡到初中“式”的运算。

小学阶段的运算主要是“数”在参与运算，而初中阶段则进入了代数式的领域——整式、分式、有理式、代数式等，更强调数学的本质，也更抽象，更能解决问题。从思维层面来说，无论是“数”还是“式”，其实质都是基于乘法分配律的运算。乘法分配律：（a+b）×c=a×c+ b×c，拓展时可以把括号内的两个数增加到三个数或更多数，如（a+b+c）×d=a×d+ b×d+ c×d，这是从量上进行拓展。还可以安排这样的思维训练：

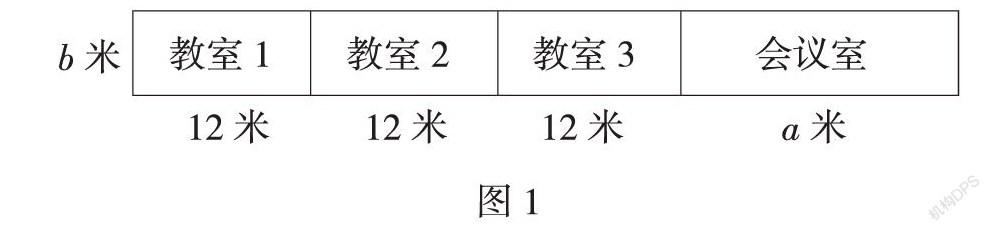
求图1所示楼层的总面积，可以这样算：12b+12b+12b

+ab=36b+ab;也可以这样算：（12+12+12+a）×b=（36+a）×b。这两种算法都是正确的，通过两种算法渗透运用乘法分配律进行合并同类项的基本方法。

另外在小学阶段，还可加强运用乘法分配律进行简便运算的各种变式练习，如：4.44×3.3+2.22×3.4=（2.22×2）×3.3+2.22×3.4=2.22×6.6+2.22×3.4=2.22×10=22.2;3333×2222÷6666=（3×1111）×（2×1111）÷（6×1111）=1111。通過让学生找相同的“数”（即相同的“项”），体会“合并”的数学思想方法。

从“数”到“式”，虽然外在“形”的变化很大，但实质上与小学阶段学过的运算律和运算性质是一致的。在小初衔接中，我们就要抓住这一“变”与“不变”的辩证关系，进行渗透。如整式的运算中，去括号是一个易错点，其实去括号也可以利用小学阶段的乘法分配律或减法的性质来说明。因此在小学阶段，应加强运用运算定律和运算性质的训练，达到知识迁移的目的。

三、推理：体会思维的延展

教材的知识体系是根据学生的年龄特征和认知规律交替螺旋上升编排的，学生的思维要经历不同阶段的延伸、拓展和丰富，由浅入深，最终形成清晰和完整的概念。因此，我们要建立小初衔接的整体理念，主动进行思维推理。如苏教版数学五年级下册安排了《用字母表示数》，其中有涉及“平方”的知识，即“a×a可以写成a·a，也可以写成a2，a2读作a的平方”。在六年级上册《长方体和正方体》中涉及“立方”的知识，即“a·a·a也可以写成a3，读作a的立方，a3表示三个a相乘”。在七年级上册《有理数》中，则对“有理数的乘方”进行了系统的教学，指出：“一个数的二次方，也称为这个数的平方;一个数的三次方，也称为这个数的立方。”以此沟通前后知识间的联系，明确“平方”和“立方”的实质都是“求相同因数的积的运算”。

小学阶段关于“平方”和“立方”的学习主要是让学生理解它们的意义、读法和写法，以及作为计量单位（如cm3、m2）的表示方式和含义。而到了初中，“乘方”则作为一级运算直接参与到有理数的混合运算中。因此，我们在小学阶段可以渗透以下几个方面的教学：

首先，让学生理解a2和a3的意义，a2=a×a，表示2个a相乘;2a=a+a，表示2个a相加。对比两者在“形”与“意”方面的异同。也可以让学生说说b3表示的意义。

其次，适当安排简单的乘方运算，如32=3×3=9，43=4×4×4=64。在运算的时候，强调让学生写出过程，即几个几相乘，以加深对乘方意义的理解。除了求整数的乘方外，还可以安排小数和分数的乘方运算，如0.12=0.1×0.1=0.01，0.23=0.2×0.2×0.2=0.008。需要特别指出的是，求某个分数的二次方或三次方，在形式上应该用小括号把分数整个括起来，同时分子和分母都要参与运算。

第三，渗透含有乘方的混合运算的运算顺序。虽然含有乘方的混合运算是七年级的全新内容，但小学阶段其实也有所涉及。如圆的面积计算公式S=πr2，圆柱的体积计算公式v=πr2·h，学生都知道要先算“半径的平方”，再依次计算其他步骤。教师可强调类似含有“平方”的需要优先计算，并安排一些练习让学生计算和体会，如32-23，82-14，8+22，等等。需要注意的是，含有乘方的混合运算，除乘方运算本身外，其他以一步为宜。

最后，在六年级总复习阶段，复习到“平方”和“立方”的知识时，也可以进行一下适当拓展，如：10×10写作102，10×10×10写作103，那10×10×10×10可以写作怎样的形式呢？让学生通过找规律的形式，合情推理，为后续学习做铺垫。

总之，当小初过渡中思维实现了无缝衔接，其他诸如教学方式、知识内容、学习习惯等方面的问题也就迎刃而解了。