考虑系统稳定性的新能源优化配置方法

李娟

（国家电投集团广西电力有限公司运营服务分公司，广西 南宁 530003）

更靠近负荷的间歇性新能源发电的接入方式，不但具有节能减排、降低终端用户费用的作用，而且节省了远距离输电线路损耗和提高供电可靠性等优点，受到了世界广泛的关注。如何将间歇性新能源安全、可靠的接入电网是新能源并网研究的热点问题之一。

间歇性新能源并网对电网运行的影响主要由接入位置和容量决定，优化安装位置和容量不仅可以保证新能源接入的安全稳定运行，还可以降低网损、改善电网电压、提高网络线路的负载能力等。目前不少学者对间歇性电源分布式接入微电网、低压配网和局部电网的优化配置开展了优化模型和优化方法的广泛研究。文献[6]进行了间歇性能源和储能的模型优化，采用了可行容量评估的方法进行容量配置，文献[7]以网损最小和电压最优为目标函数；文献[8]利用简单遗传算法实现了最大化系统负荷裕度和分布式接入的效益；文献[9]采用链式配电网络及电源的功率模型；文献[10]采用整数和非线性规划的混合方法，优化电源的接入点和注入系统容量，达到稳定电压稳定裕度的目的。

本文提出针对局部电网新的优化方案——以电网系统薄弱点处发电机的静态稳定储备系数最大和输电线路的网损最小为目标函数，采用小生境遗传算法。采用该方法不仅提升系统的静态稳定性，有效改善系统运行的电压，而且配电网的网损最小化，提高经济效益。

1 优化配置的数学模型

1.1 静态稳定储备系数

根据静态稳定极限的计算式（1）

式中，E为发电机的空载电势，V为并网母线电压，X∑为系统电抗。

间歇性电源并入系统运行，可能提高母线电压运行水平V、减小系统的等效电抗X∑，从而达到提高系统静态稳定极限PGM。

常用静态稳定储备系数Kp表示各发电机的静态稳定裕度，如式(2)：

式中，PGM为静态稳定的极限输送功率；PG0为发电机输出的有功。

多机系统中发电机的静态稳定储备系数的计算步骤如下：

（1）常规潮流计算，得到各发电机的内电动势Eg，并得到负荷等值阻抗。

（2）在发电机节点后加一个内电动势节点，将各负荷等值阻抗并入网络的导纳矩阵，消去原网络的全部节点，则只有发电机内电动势节点的导纳矩阵YG。

（3）依据公式(3)求出全部发电机的功率极限Pgm。

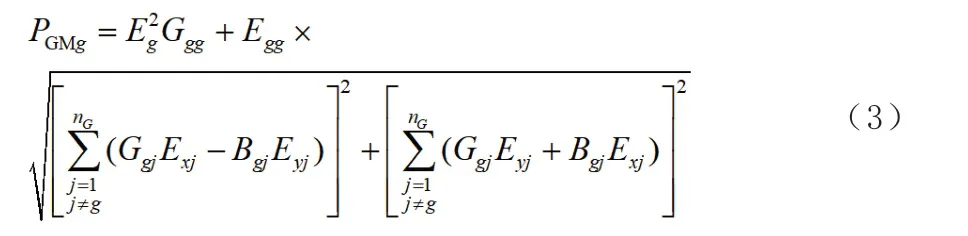
式中，Exj和Eyj分别为各内电动势的实部和虚部；Ggj和Bgj分别为导纳YG矩阵中元素Ygj的实部和虚部。

（4）依据公式(2)就可以求出发电机g的Kpg。

本文选取储备系数最小的发电机结点为系统薄弱点，则系统薄弱点的储备系数如表达式（4）：

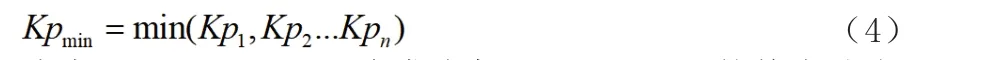
式中，Kp1、Kp2…Kpn为发电机1，2… …n的静态稳定储备系数。

1.2 间歇性电源优化模型

为了确保整个电网在接入分布式电源后能够安全稳定运行，本文提出以电网最薄弱点处发电机的静态储备系数Kp最大为优化目标。

目标函数

等式约束的潮流方程：

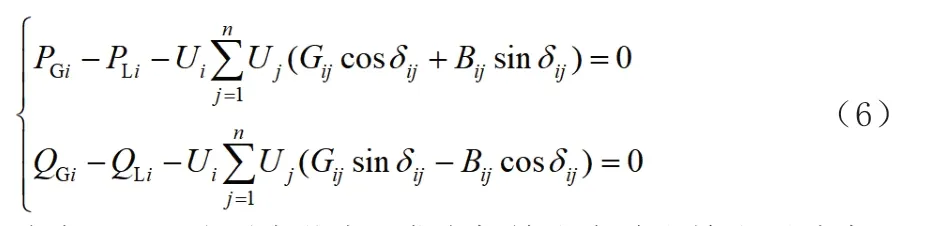
式中，PGi、分别为节点i发电机输出有功和输出无功力；分别为节点i处的有功无功负荷；Ui、Uj分别是节点i和j的电压幅值；δij为节点i和j的电压相角差。

不等式约束：

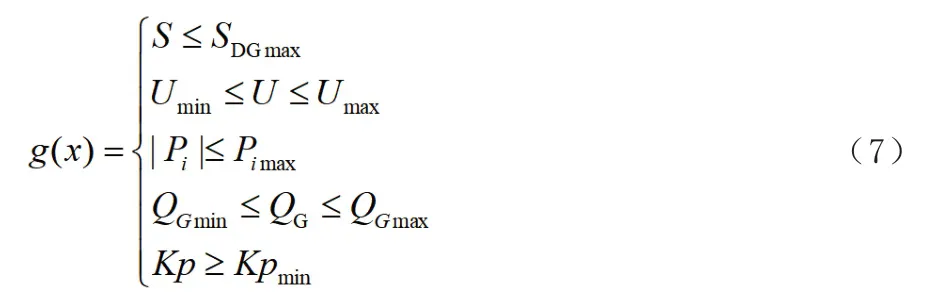
式中，S、SDGmax分别为间歇性电源的容量及其最大值；U、Umin、Umax分别为系统节点电压及最小值和最大值；Pi、Pimax分别为支路的有功功率及其最大允许值；QG、QGmin、QGmax分别为发电机的无功及最小值和最大值；Kp、Kpmin分别为静态储备系数及其最小允许值，Kpmin在正常运行方式下，一般取15%，非正常方式下可取10%。

2 小生境遗传算法

采用小生境遗传算法对电网中的间歇性电源（DG，Distributed Generation）进行优化配置，具体流程如图1所示，步骤如下：

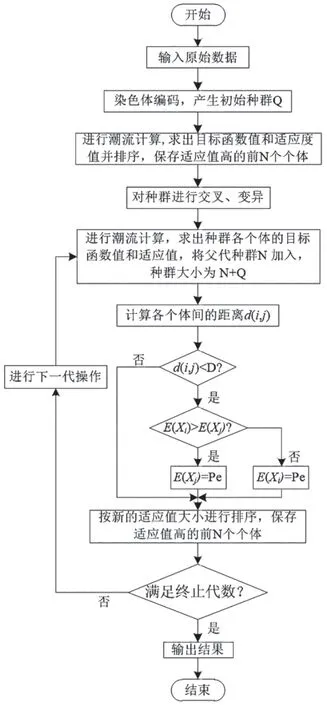
图1 本文的方案算法的流程

（1）输入原始数据，对DG的位置和容量进行编码，生成初始种群。采用十进制编码，包含间歇性电源的位置和容量两个元素，如式（8）：

式中，C1表示间歇性新能源的安装位置，C2表示间歇性新能源的安装容量。

（2）计算目标函数值：包括网损和静态稳定储备系数，计算适应度函数值，保留当前最好的N个个体。

（3）对种群Q进行交叉与变异，通过潮流计算，得到每个个体的目标函数值及适应度函数值，把父代种群加入，种群大小为N+Q。

（4）依据式(8)计算个体间的距离d(i，j)，修正个体的适应度函数。淘汰距离范围内适应值小的个体，保留最优的N个个体。

（5）当前遗传代数m≤M（M为设定的遗传代数），则跳回步骤（3），若m≥M，得出最优解，输出计算结果。

3 算例及结果分析

以IEEE-30节点系统为例，采用Matlab软件，该系统有功负荷为283.4MW，无功负荷为126.2Mvar，系统结构如图2所示。

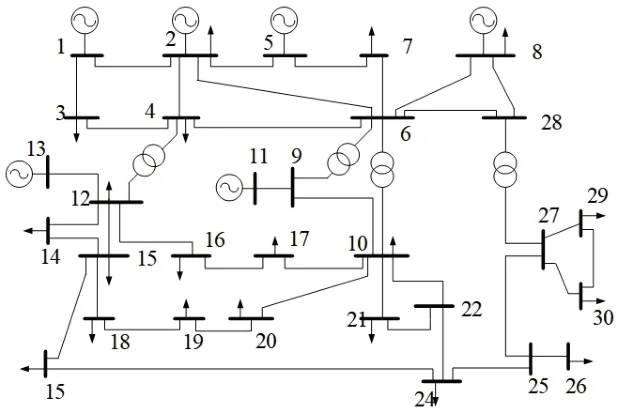
图2 IEEE-30节点系统结构图

各个参数的选取：

（1）C1、C2参数的确定。由于节点1为平衡节点，故可安装DG的位置数为29，C1的取值范围为0～29；C2的取值范围为：

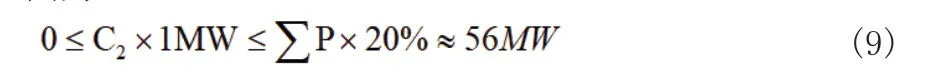
式中，∑P为系统的总有功负荷283.4MW，即C2∈[0，56]。

（2）其余参数选取。种群规模为50，变异概率0.0778，交叉概率0.7，代沟0.9，最大遗传代数50，Pe取0.001。

计算结果如图3和表1所示，图3中横坐标为迭代次数。

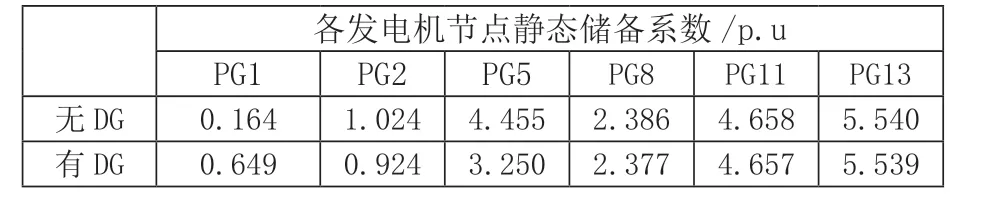
表1 网损和静态储备系数的优化结果

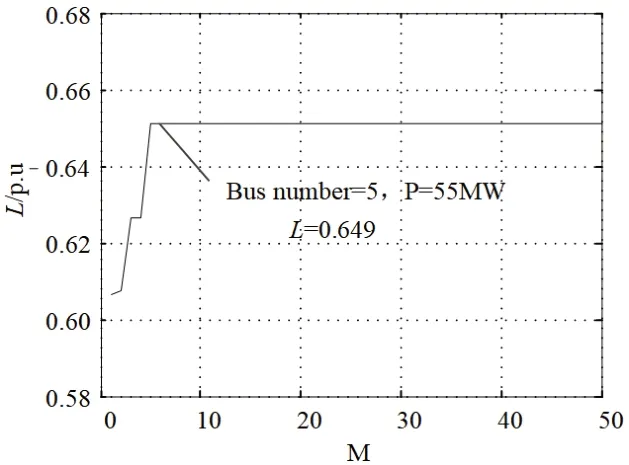
图3 本文算法迭代结果

由图3可知，经过5次遗传迭代计算可得出IEEE-30节点系统的最佳安装位置是节点5，容量为55MW。

表1为间歇性电源接入后，系统的有功网损与各发电机节点的静态储备系数的大小。由表1可知，系统薄弱点处，发电机1的静态储备系数由16.4%提升为64.9%，提高了295.73%。

图4(a)和4(b)分别为间歇性电源安装在不同位置对应薄弱点处的静态储备系数。

图4表明，当间歇性电源安装在节点5时，系统薄弱点处的发电机静态储备系数最大。由此验证了节点5为减小系统网损和提高系统静态稳定储备系数的最佳安装位置。

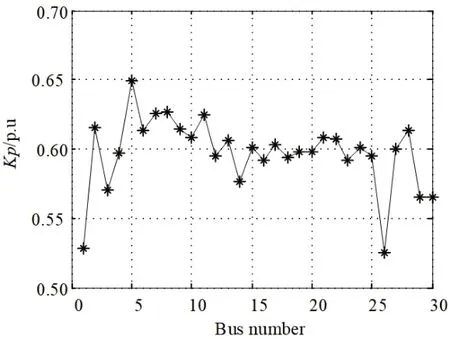
图4 安装在薄弱点的静态储备系数

间歇性能源接入前后节点电压如表2。

表2 DG接入前后IEEE 30节点电压

比较接入前后的各节点的电压，其最大的电压差为0.0006p.u，可见间歇性电源的接入不影响电网的正常运行。

算例表明，本文所提出的间歇性电源优化配置方法，可以有效地改善系统的运行条件，提升系统的静态稳定性。

4 结语

针对间歇性电源接入对电网的安全稳定性和经济性，本文提出的方法使系统薄弱点处发电机的静态储备系数提高为原来的2.96倍，网损降低49.96%，显著改善网络运行性能，为间歇性新能源接入系统提供一种新思路。