基于无应力状态法的多跨连续梁桥合龙研究
2021-12-21叶再军徐宏广
叶再军 徐宏广
(1.湖北省交通运输厅工程质量监督局 武汉 430014; 2.杭州建工集团有限责任公司 杭州 310013)
预应力混凝土连续梁桥具有变形小、结构刚度好、行车平顺舒适、伸缩缝少、养护简易等优点,是一种常见的桥梁结构,一般采用先悬臂再合龙的方式施工。合龙是悬臂法施工的关键环节,涉及合龙段浇筑、合龙预应力束张拉、临时固结的拆除等多个复杂工序。目前,悬臂法施工的预应力混凝土连续梁桥常见的合龙施工顺序有先边跨后中间跨,或先中间跨再边跨,不同的合龙顺序或合龙束张拉顺序直接影响着结构次内力、内力重分布和位移变化的情况,对成桥状态的内力和位移会产生一定影响[1]。孙全胜等[2-5]以连续刚构桥和连续梁桥为例,分析比较了不同合龙顺序对连续桥梁成桥内力和位移的影响,并给出了优化的合龙方案,但并未深入分析不同合龙顺序下成桥内力和位移不同的原因。本文以某多跨预应力混凝土连续梁桥为研究对象,分析不同合龙方式对连续桥梁成桥状态的影响及产生影响的本质原因。
1 无应力状态法理论
无应力状态法是秦顺全院士提出的一种解决桥梁分阶段施工的控制理论方法[6],它是一种利用结构的无应力长度和无应力曲率这一个抽象的控制量将桥梁结构安装的中间状态和成桥状态联系起来对桥梁进行分析的方法。该理论认为桥梁结构无论实际形成过程如何,只要最终的成桥结构构件单元的无应力长度、无应力曲率、外荷载,以及支承条件一定,则最终成桥结构的内力状态和位移状态与结构的形成过程无关[7]。对多跨连续梁而言,梁段的无应力曲率在构件安装时就已确定,在后续施工过程中,随着结构体系和外荷载的变化,结构的内力和位移会发生变化,但结构的无应力曲率不会随结构体系和外荷载的变化而变化。已有研究将该方法应用于桥梁的施工控制研究,取得了较好的效果。
2 工程概况及有限元模型建立
2.1 工程概况
某9跨预应力混凝土变截面箱形连续梁桥,桥跨布置图见图1。其跨径布置为:50.25 m+7×90 m+50.25 m。

图1 1/2桥型布置图(单位:cm)
该桥主梁为纵、横、竖三向预应力结构,纵、横向预应力体系采用高强度低松弛钢绞线,竖向预应力筋采用直径32 mm精轧螺纹钢筋。主梁混凝土强度等级为C50,桥墩混凝土强度等级为C40。
本桥采用悬臂浇注法施工,由于墩顶所设永久支座不能承受施工过程中产生的不平衡弯矩,在悬臂浇注阶段必须将主梁与各主墩在墩顶处临时固结形成结构稳定的T形刚构,从1号墩到8号墩共形成8个T形刚构。各T形刚构除墩顶的零号块外,每边各分为10个节段,纵向长度为5×3.5 m+5×4 m,墩顶处的零号块长13 m,边、中跨合龙段长均为2 m。墩顶处的零号块采用搭设支架浇注混凝土施工,当零号块混凝土达到设计强度等级的80%后进行预应力筋的张拉。零号块预应力筋张拉完毕后,在零号块的左右两侧对称地进行1、2号块挂篮的安装,接着利用挂篮悬臂浇筑1、2号块的混凝土。按与1、2号块相同的施工方法,以每2个节段为1组,对称地进行其余18个节段的挂篮安装与混凝土浇筑施工,直到该T形刚构左右两侧的梁段全部浇筑完毕。待梁段的混凝土达到规定的强度等级后即可进行预应力筋的张拉及后续的挂篮拆除工作,从而完成1个T形刚构的施工。当全部的8个T形刚构施工完毕后,再将各合龙口按一定顺序合龙和张拉合龙预应力筋。原设计方案为从左、右边跨向中间跨对称地逐跨依次合龙施工,后结合现场施工状况,对合龙方案进行优化,提出了2种优化后的合龙方案。方案I为原设计方案,方案II、III为优化方案,3种合龙方案具体如下。
方案I。先合龙边跨(即第1、9跨),再按顺序逐次合龙次边跨和次中跨(即第2、8跨、第3、7跨和第4、6跨),最后合龙中跨(即第5跨),并在合龙时张拉全部合龙束预应力、拆除相应墩顶临时固结,方案I合龙步骤图见图2。

图2 方案I合龙步骤
方案II。先合龙边跨(即第1、9跨),再合龙其余奇数跨(即第3、5、7跨),再合龙第2、8跨和第4跨,最后合龙第6跨,并在合龙时张拉全部合龙束预应力、拆除相应墩顶临时固结,方案II合龙步骤图见图3。
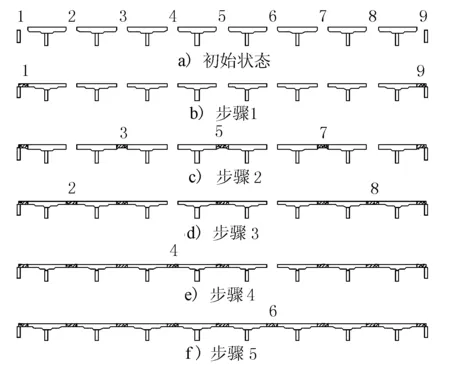
图3 方案II、III合龙步骤
方案III:与方案II合龙的顺序完全相同,不同之处是第3、5、7跨合龙时,先张拉部分底板合龙束,全桥合龙完成后再张拉剩余底板合龙束。本桥第1、9跨底板合龙束编号为B1~B5,第2~8跨底板合龙束由短束到长束分别为B6~B11,第3、5、7跨合龙时,先张拉部分底板合龙束,即第3、5、7跨合龙时先张拉B10、B11底板束、拆除相应墩顶临时固结,其余跨合龙时则与方案II一样张拉全部底板合龙束预应力、拆除相应墩顶临时固结,全桥合龙后再张拉第3、5、7跨的B6~B9等底板合龙束。
2.2 有限元模型
为比较3种施工方案对成桥过程的影响,采用有限元分析软件midas Civil建模进行模拟分析。在利用midas Civil建模时,将结构简化为平面结构,各梁段离散为梁单元,由于本桥桥墩刚度较大,在模型中不考虑墩柱的影响(即按桥墩刚度无限大来考虑),按设计的施工节段进行梁单元划分,不同合龙方案通过在模型中建立不同施工过程进行模拟,为便于不同模型之间的对比分析,在模型中不考虑混凝土材料收缩与徐变的影响。
3 结果与分析
3.1 成桥状态主梁弯矩
3种方案的成桥状态主梁弯矩图见图4。由图4可见,3种方案主梁成桥弯矩存在一定差异,方案I最大正弯矩为34 920 kN·m,位于次边跨(第2、8跨)边跨侧1/4跨附近,最大负弯矩为98 976 kN·m,位于第2、7号墩顶;方案II最大正弯矩为39 994 kN·m,也位于次边跨(第2、8跨)边跨侧1/4跨附近,最大负弯矩为125 000 kN·m,也位于第2、7号墩顶;方案III最大正弯矩为37 755 kN·m,位于第6跨1/4跨附近,最大负弯矩为96 264 kN·m,也位于第2、7号墩顶。

图4 3种合龙方案主梁成桥弯矩图(单位:kN·m)
3.2 成桥状态主梁挠度图
3种方案成桥状态主梁挠度图见图5。

图5 3种合龙方案主梁成桥挠度图(单位:mm)
由图5可见,3种方案主梁成桥挠度差别较大,方案III挠度最小,方案I次之,方案III最小。各方案向上、向下的最大位移分别为:方案I向下的最大位移为50 mm,向上的最大位移为31 mm;方案II向下的最大位移为97 mm,向上的最大位移为51 mm;方案III向下的最大位移为34 mm,向上的最大位移为15 mm。方案III与方案II挠度变化趋势基本一致,但方案III的挠度值较方案II有明显减小。
4 合龙方案对成桥状态影响的机理分析
本桥预设的3种不同的合龙施工方案中,成桥状态时桥梁的外荷载和支承条件均相同,根据无应力状态法理论,造成成桥内力和位移状态不同的原因只能是桥梁的无应力长度或无应力曲率。本桥从悬臂施工到合龙直至成桥的过程中,不同方案在合龙前的悬臂施工过程是一致的,故主梁的零号块、各悬臂节段和边跨支架施工段的无应力状态量是相同的。若主梁的无应力状态量不同,只能是合龙段的无应力状态量不一致。这里指的合龙段无应力状态量是保证满足主梁在合龙段处弹性曲线连续的条件下进行合龙段无应力安装的无应力状态量。
在满足合龙段处主梁弹性连续合龙段无应力安装的条件下,合龙段无应力曲线可表示为[3]
(1)
(2)
由式(1)、(2)可求得合龙段两端无应力曲率为
(3)
(4)
式中:ui、vi、θi和uj、vj、θj分别为合龙段两端水平向、竖向和转角位移;v(x)为合龙段无应力曲线;l为合龙段无应力长度;κi、κj分别为合龙段两端无应力曲率。
分别从方案I、II、III中提取各合龙段合龙前两侧悬臂端节点位移列于表1中,在满足主梁合龙段处弹性曲线连续的条件下,两侧悬臂端节点的位移即为合龙段两端的位移。将两侧悬臂端节点位移值代入式(2)~(4)可得各合龙段无应力长度和两端无应力曲率,计算结果分别列于表2、表3。据表2、表3可知,方案I与方案II、III相比,合龙段2~8的无应力量不一致;方案I与方案III相比,合龙段2、4、6、8的无应力量不一致。

表1 各合龙段两端合龙前位移表

表2 各合龙段无应力长度表 mm

表3 各合龙段两端无应力曲率表
为进一步探讨不同合龙方案时,成桥状态下的内力和位移不同的本质原因是否与合龙段无应力状态量有关,在有限元模型中对悬臂端节点施加节点强制位移荷载,使不同合龙方案下各合龙段合龙前两侧悬臂端节点位移一致,待全桥合龙完成后再卸除所施加的节点强制位移荷载,使合龙时不同合龙方案各合龙段无应力长度和无应力曲率一致,再对不同合龙方案的有限元模型的成桥内力和位移状态进行比较。
在方案II的有限元模型相应节点上施加节点强制位移荷载,使方案II各合龙口两侧悬臂端节点位移值与方案III一致,待全桥合龙后卸除节点强制位移荷载,修改后的方案II主梁成桥弯矩图及位移状态见图6和图7。

图6 修改后的合龙方案II主梁成桥弯矩图(单位:kN·m)
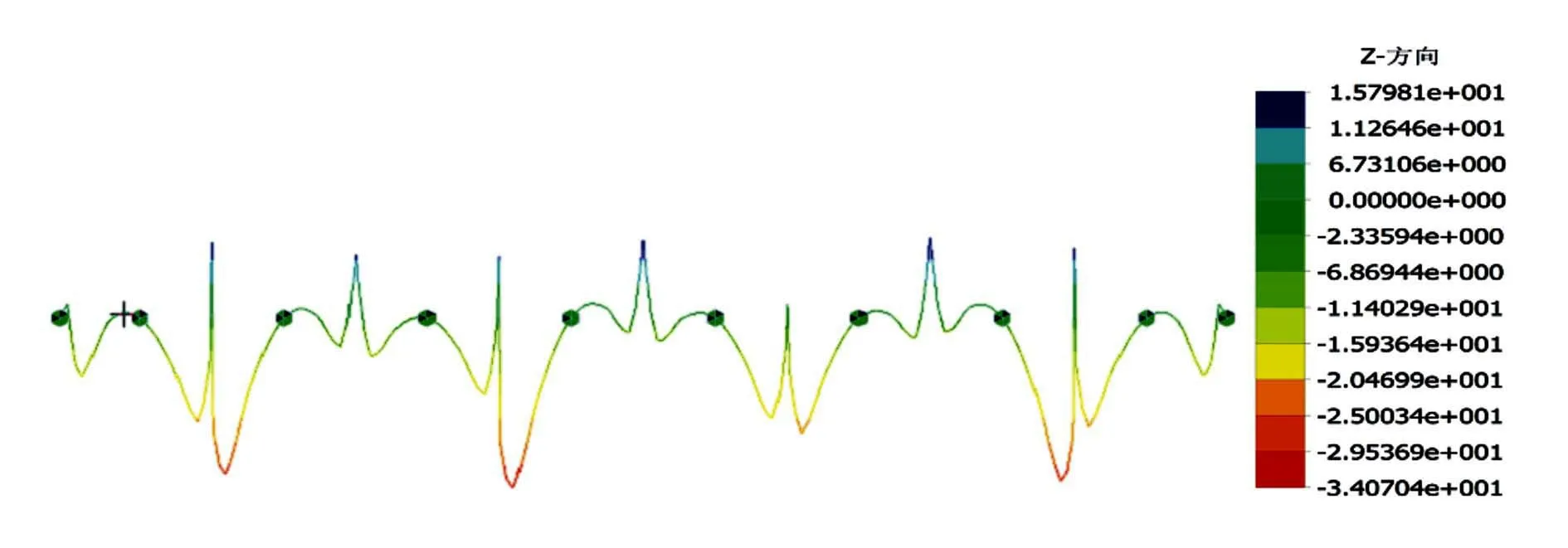
图7 修改后的合龙方案II主梁成桥挠度图(单位:mm)
对比图4(b)和图5(b)可知,方案II经修改后其桥梁成桥弯矩和位移状态与原方案III一致。选取方案I和方案II做上述对比分析结果亦如此。由此可见,在不改变原有合龙顺序和合龙束张拉顺序的条件下,通过在合龙前对悬臂端施加适当荷载,使合龙段无应力状态量一致,不同合龙方案下桥梁的成桥内力和位移状态一致,说明造成方案I、II、III最终成桥状态不同的本质原因为合龙段无应力状态量不同。
5 结论
1) 多跨连续梁不同合龙顺序或合龙束张拉顺序下成桥内力状态和位移状态不同,其本质原因是在不同合龙顺序或合龙束张拉顺序时,合龙前悬臂端产生的转角位移不同,从而造成合龙时合龙段无应力状态量的不同。
2) 多跨连续梁在不同合龙顺序或合龙束张拉顺序时,其成桥的内力和位移状态一般不同,如能在合龙前采用一定的措施保证合龙段处两悬臂端的转角一致,使不同合龙顺序或合龙束张拉顺序合龙段两端点处无应力状态量一致,则桥梁成桥的内力和位移状态在不同合龙顺序或合龙束张拉顺序时亦可保持一致。
理解多跨连续梁结构的无应力状态量意义,对处理多跨连续梁在施工控制中的一些问题有很大的帮助,可应用无应力状态法理论,对多跨连续梁施工方案进行适当优化,在连续梁全部合龙后,桥梁结构的无应力状态量已确定,方案III中各合龙段底板合龙束的张拉先后顺序不改变主梁无应力状态,可根据现场实际情况选择合适的张拉顺序,其对最终的成桥状态不会产生影响。
