平均风荷载作用下斜列三方柱的干扰效应研究
2021-12-21廖坤阳
廖坤阳
(福建林业职业技术学院 建筑工程系,福建 南平 353000)
方柱在实际工程中应用广泛,例如桥墩、桥塔、海上钻井平台、超高层建筑群等.与圆柱类似,方柱作为最典型的钝体结构之一,在实际工程应用中通常也不是以单一的形式存在,它们往往按照一定的方式进行排列和布置,以“组”或“群”的形式呈现.多方柱的绕流伴随着流动的分离、碰撞、再附着、漩涡脱落等十分复杂的流动现象,这些都是影响结构抗风的重要因素.因此,研究多方柱在不同形式下的排列和布置时的流动特性就显得十分有意义.
20 世纪七八十年代学者们就对方形截面的钝体开展了研究.在不同风向角下,Kwok[1]通过风洞试验,确定了方形柱体周围的压力分布.研究发现,湍流度的增加显著地改变了方柱的压力分布和横向力特性.Du 等[2]采用风洞试验的方法研究了间距比为1.25~5.0 时,2 个相同方柱的气动特性,得到了上、下游方柱的平均气动力系数、平均压力系数和斯托罗哈数.黄剑等[3]在均匀流场中研究了等高双方柱在3 种不同布置情况下平均风压的阻塞效应,结果表明,阻塞度的变化范围为2.7%~10.0%,平均风压系数的阻塞效应和单体建筑的较为相似,阻塞效应对模型迎风面平均风压的影响可以忽略;但侧面和背风面平均负压随阻塞度增加显著增大.Liu 等[4]研究了间距比为1.5~9.0,雷诺数Re=2.0×103~1.6×104的情况下串列方柱的流动特性.试验发现,雷诺数的变化可以使临界间距发生在不同位置,且其递增时的临界间距大于递减时的临界间距.文献[5-6]表明:对于多柱体绕流而言,间距比与风向角是影响其气动特性的关键因素,且多柱体绕流存在临界间距比,在不同的间距比内绕流形态也有所不同.国内外学者针对单、双方柱绕流问题进行了大量的研究,而对于三方柱绕流的研究相对较少,对于方柱的布置方式多为串列和并列且间距比也不理想,干扰机理的研究不够清晰,且研究方法多为数值计算.
本文针对上述情况,依托某大桥,采取刚性模型测压风洞试验的方法,主要研究了不同间距比下斜列三方柱绕流时流场流态的变化对各方柱平均风压的干扰效应.
1 风洞试验概况
风洞试验在某大学大气边界层风洞的低速试验段中进行,试验装置如图1 所示.
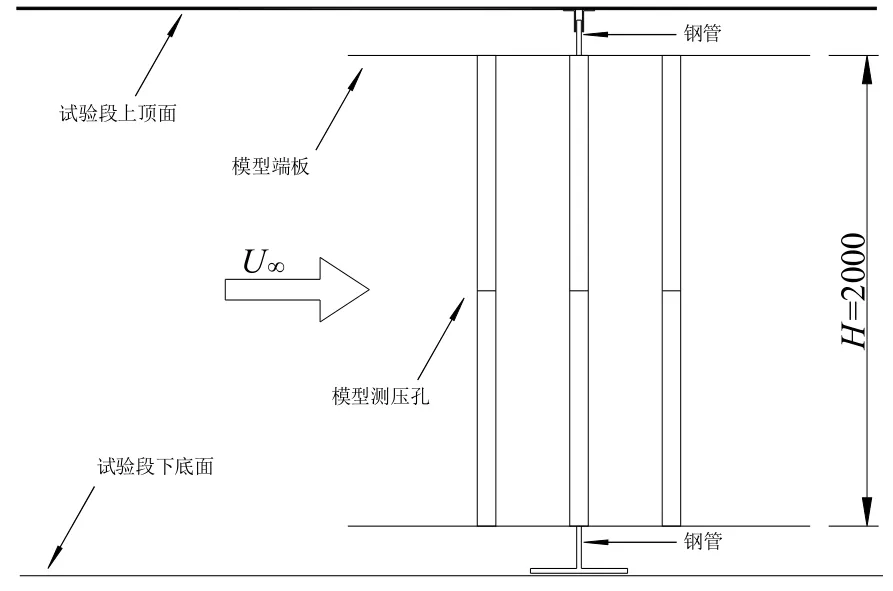
图1 试验模型与试验装置/mm
由图1 可知,模型连同模型两端的端板通过上、下2 根钢管竖直固定,下端钢管固定在试验段转盘上,旋转转盘可改变模型的来流风向角.如图2所示,试验风向角α的变化范围为0°~90°,模型的高度H=2 000 mm,横断面边长D=100 mm,可知试验满足阻塞度的相关要求.如图3 所示,沿模型高度方向中央位置处布置1 圈测压孔,考虑到流场参数在模型棱角附近变化较为剧烈,故对这些位置的测压孔进行加密.模型表面不同位置测压孔的风压通过电子压力扫描阀测得.为消除模型的端部效应,在模型两端布置了端板.
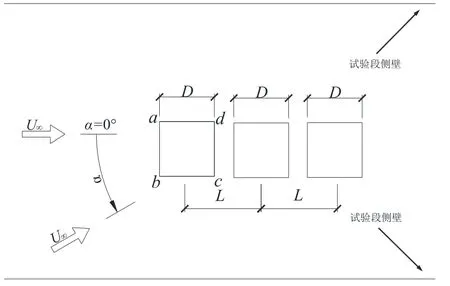
图2 试验模型的尺寸及相对位置/mm
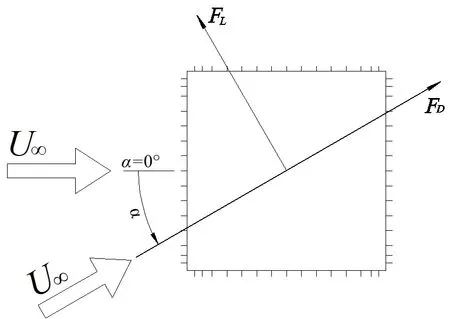
图3 试验模型的测点布置
为保证结果的可靠性,首先对单方柱进行试验,并将试验结果与已有结果进行对比;在保证可靠性后,再对不同间距下的斜列三方柱进行试验.其中,间距比L/D(L为2 个方柱的中心距,D为方柱的边长)的取值分别为1.2,1.4,1.6,1.8,2.0,2.5,3.0,3.5,4.0,4.5,5.0,6.0,7.0 和8.0.
2 试验结果分析
2.1 不同风向角下单方柱的平均风压分布
不同风向角下方柱的风压分布可用无量纲参数风压系数表示,定义为
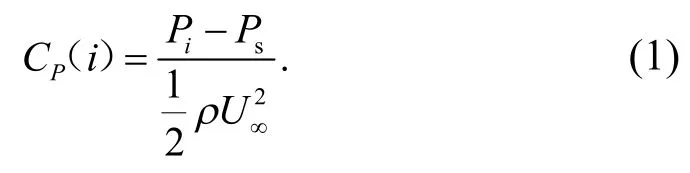
其中,Pi是模型表面某测点处测得的瞬时压力信号的时间序列;Ps是参考点处的静压值;ρ为空气密度;U∞为模型远前方来流的风速.
平均风压系数CP,mean可定义为
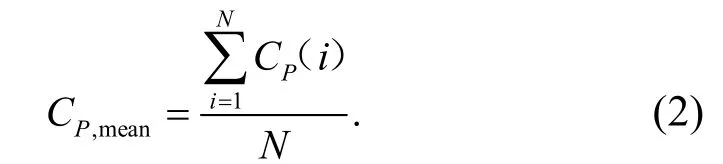
其中,N为采样点数,本试验为9 900 个.
图4 显示了不同风向角下单方柱各测点的平均风压系数.为方便论述,将方柱4 个角点分别标记为a,b,c和d,如图2 所示.这样方柱4个面可分别标记为面ab、面bc、面cd和面da.
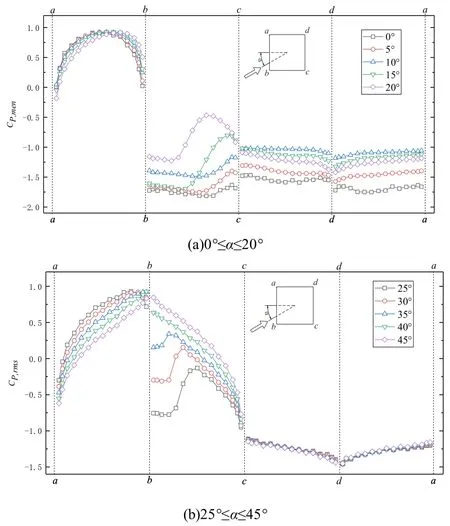
图4 不同风向角时单方柱各测点的平均风压系数
从图4 中可以看出:
1)风向角的改变对面ab和面bc上测点的平均风压系数的影响要明显大于对面cd和面da的影响.
2)当0°≤α≤20°时,面ab上测点的平均风压系数基本为正值,呈现出中间大两端小的分布特征,且随风向角的增大变化很小.
3)当25°≤α≤45°时,随着风向角的增大,面ab上测点的平均风压系数逐渐减小,且靠近角点a的部分测点的平均风压系数出现负值.
4)当0°≤α≤10°时,面bc上测点的平均风压系数为负值,随着风向角的增大,平均风压系数绝对值逐渐减小.
5)当15°≤α≤45°时,随着测点由角点b向角点c靠近,平均风压系数呈先增大后减小趋势,且平均风压系数的最大值对应的测点随着风向角的增大逐渐向角点b靠近.
6)面cd和面da上测点的平均风压系数变化规律相似.当0°≤α≤10°时,随风向角增大,平均风压系数的绝对值逐渐减小;当15°≤α≤45°时,随风向角增大,平均风压系数基本没有变化.
2.2 不同风向角和间距比下斜列三方柱的平均风压分布
为方便阐述不同风向角与间距比下的斜列三方柱平均风压分布情况,将风向角范围分为3 个部分:0°≤α≤10°、15°≤α≤75°、80°≤α≤90°.为了使图像清晰美观且能反应大致规律,只选取典型间距比(L/D=1.2,1.6,2.0,2.5,3.0,3.5,4.0,6.0 和8.0).因篇幅有限,本文仅呈现出α=0°,45°和90° 3 个典型风向角下的三方柱平均风压分布结果.
图5 为α=0°时上游方柱在不同间距比下各测点平均风压系数.
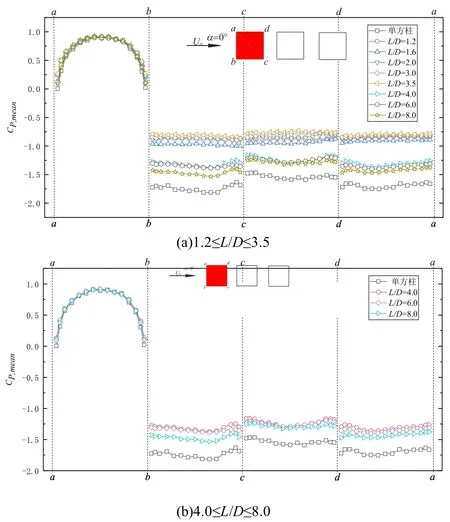
图5 0°风向角下上游方柱各测点的平均风压系数
由图5(a)可知,当1.2≤L/D≤3.5 时,迎风面ab上各测点风压系数与单方柱试验结果吻合良好且均为正值;由图5(b)可知,当4.0≤L/D≤8.0时,各测面平均风压分布规律大致与1.2≤L/D≤3.5时相同.由此可知,不同间距比下对于上游方柱的平均风压干扰效应主要集中在bc、cd和da3个面,且随着间距比的增大进一步增大了这3 个面上的平均风压系数绝对值.
图6 为α=0°时中游方柱的各测点平均风压系数.由图6(a)可知,当1.2≤L/D≤3.5 时,由于中游方柱受到上、下游方柱的干扰,其各面平均风压系数均为负值,且ab面与cd面上的平均风压系数随间距比的增大其绝对值逐渐减小;由图6(b)可知,当4.0≤L/D≤8.0 时,中游方柱各面平均风压分布出现较好的一致性.
图7 为α=0°时下游方柱各测点平均风压系数,其分布规律与中游方柱相似.
图8 为α=45°时上游方柱在不同间距比下各测点平均风压系数.由图 8(a)可知,当1.2≤L/D≤3.5 时,ab面和bc面平均风压分布规律与单方柱相似,cd面和da面平均风压系数随间距比逐渐增大接近单方柱试验结果;由图9(b)可知,当4.0≤L/D≤8.0 时,方柱各面平均风压分布与单方柱基本一致,具有良好的对称性,且方柱各面平均风压系数“分层”现象开始消失,迎风面出现由ab面向bc面过渡的现象.
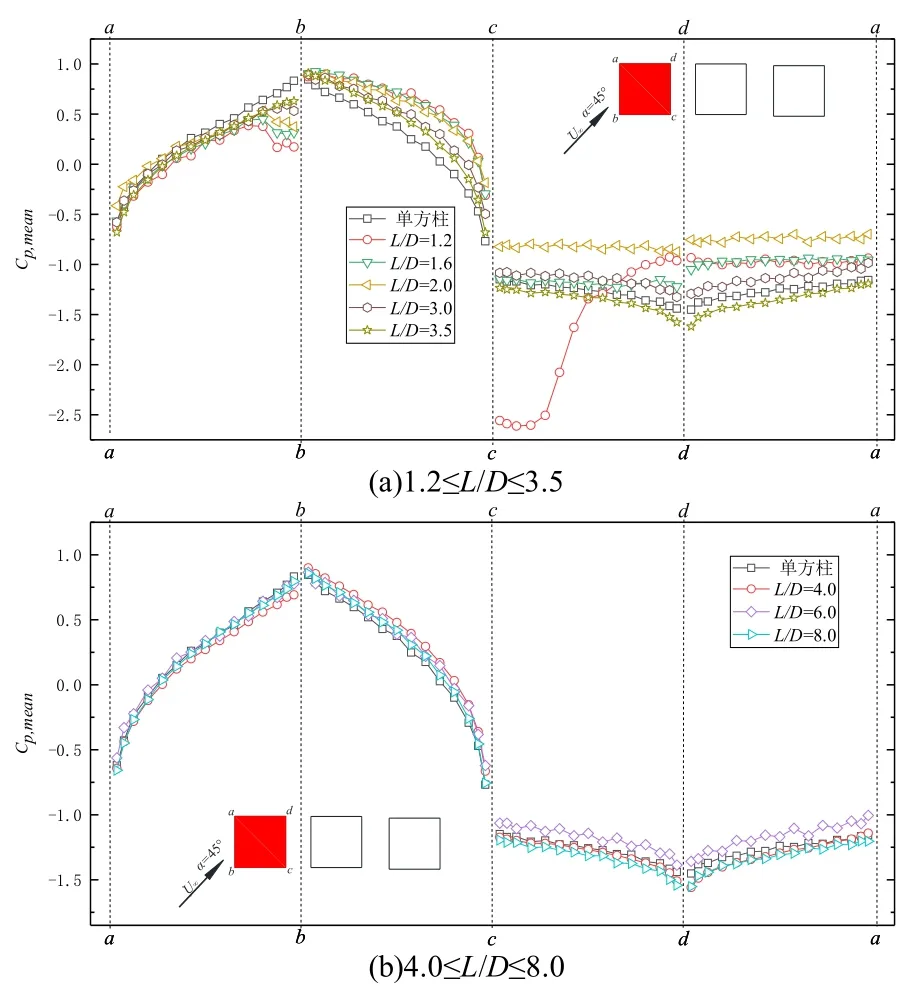
图8 45°风向角时上游方柱各测点的平均风压系数
图9 为α=45°时中游方柱的各测点平均风压系数.由图9(a)可知,当1.2≤L/D≤3.5 时,ab面平均风压系数变化较为复杂,这可能是间隙位置处产生了较强的气动干扰;由图9(b)可知,当4.0≤L/D≤8.0 时,方柱各面平均风压系数与单方柱试验结果基本相同,具有良好的对称性,角点d处出现了极小值.
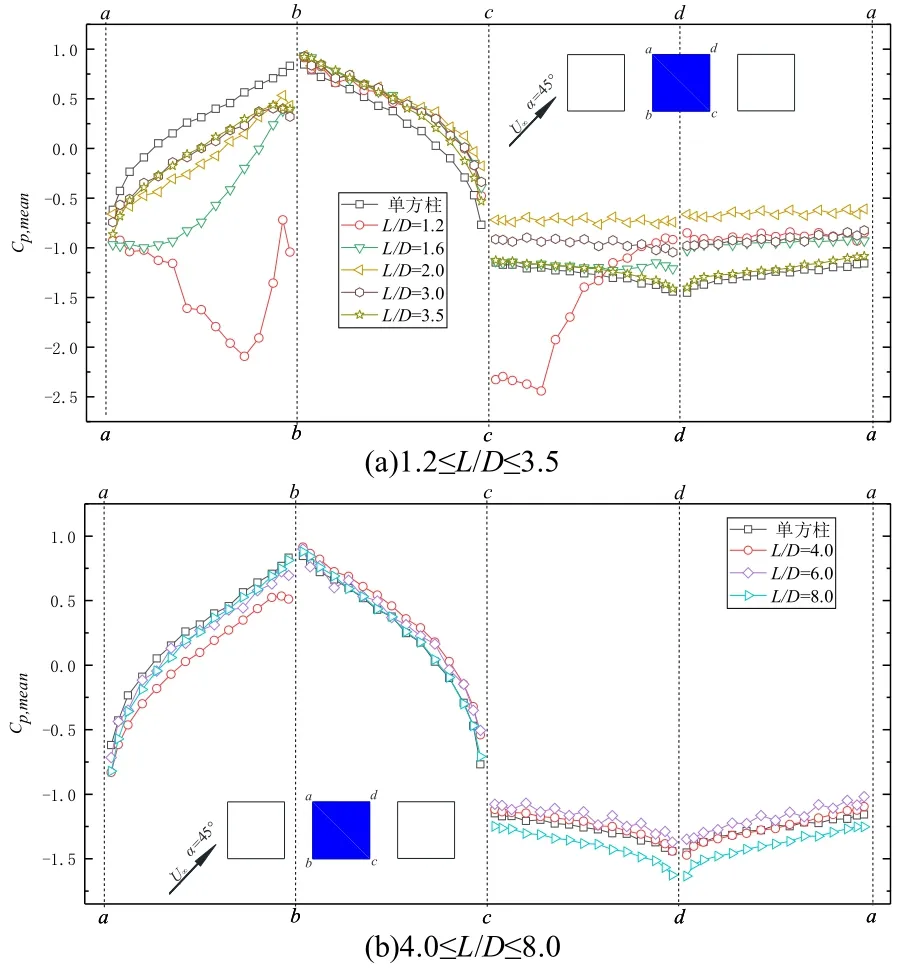
图9 45°风向角下中游方柱各测点的平均风压系数
图10 为α=45°时下游方柱的各测点平均风压系数.由图10(a)可知,当1.2≤L/D≤3.5 时,ab面和bc面平均风压系数同中游方柱相类似;cd面和da面平均风压系数基本不发生变化,从角点c到a平均风压系数呈现出“水平线”,其值基本维持在−1~−0.5,这是下游的方柱被上、中游方柱产生的分离剪切层完全包裹所致.由图10(b)可知,当4.0≤L/D≤8.0 时,ab面和bc面平均风压系数与单方柱试验结果相似;cd面和da面平均风压系数随着间距比的增大“水平线”现象消失.
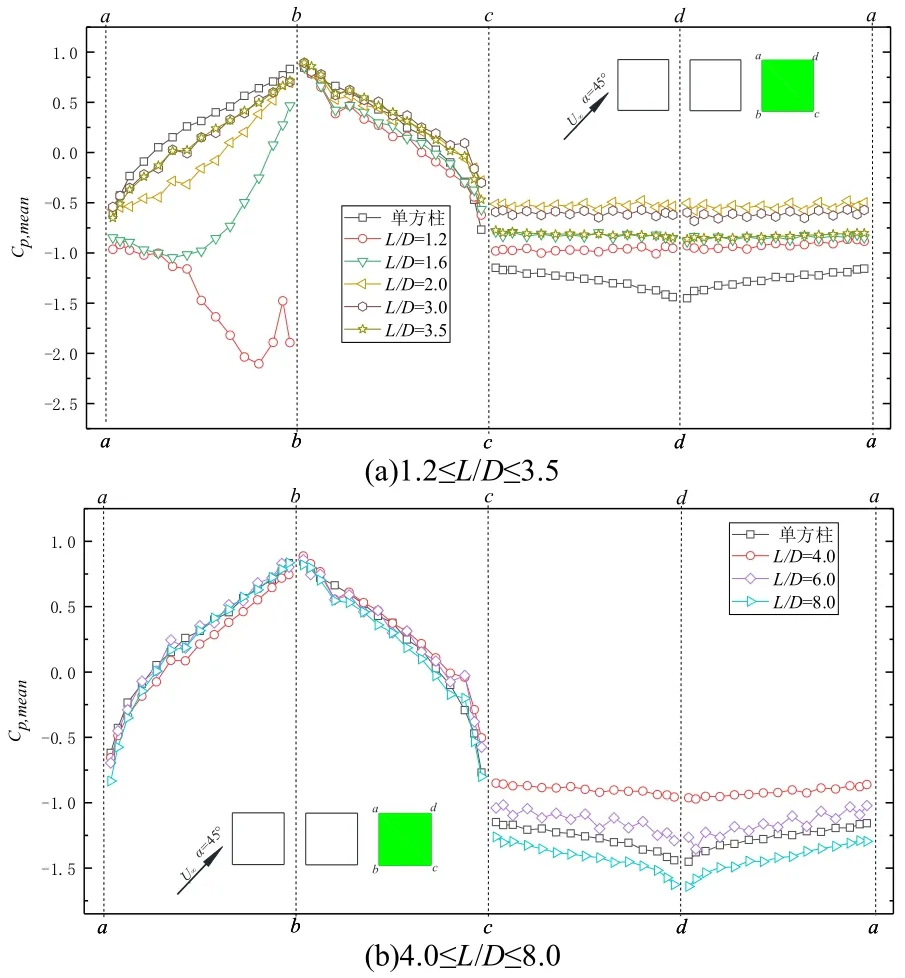
图10 45°风向角时下游方柱各测点的平均风压系数
图11 为α=90°时上游方柱在不同间距比下各测点平均风压系数.由图 11(a)可知,当1.2≤L/D≤3.5 时,ab面所有测点平均风压系数均为负值,且随着间距比增大其绝对值也逐渐增大,各测点平均风压系数沿ab面方向变化不明显.由图11(b)可知,当4.0≤L/D≤8.0 时,不同间距比下各测点平均风压系数变化情况基本一致,各面平均风压系数与单方柱试验结果接近,除bc面外,其余各面的平均风压系数均为负值.
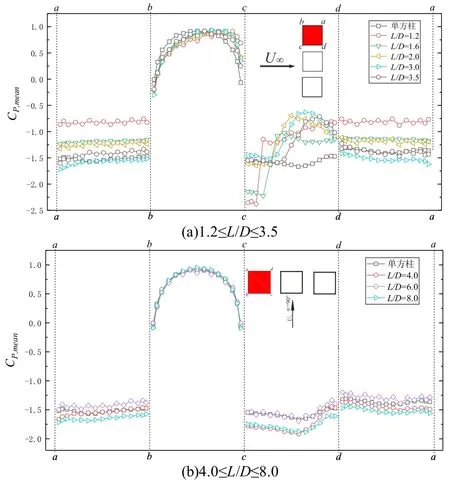
图11 90°风向角时上游方柱各测点的平均风压系数
图12 为α=90°时中游方柱的各测点平均风压系数.由图12(a)可知,当1.2≤L/D≤3.5 时,ab面所有测点平均风压系数均为负值,其值从a点到b点随L/D增加逐渐减小;bc面从b点到c点,平均风压系数先增大后减小.不同间距比下各测点平均风压系数与单方柱试验结果有较好的一致性,bc面各测点平均风压系数均为正值.由图12(b)可知,在4.0≤L/D≤8.0 时,不同间距比下各测点平均风压系数变化情况基本一致,各面平均风压系数与单方柱试验结果接近.
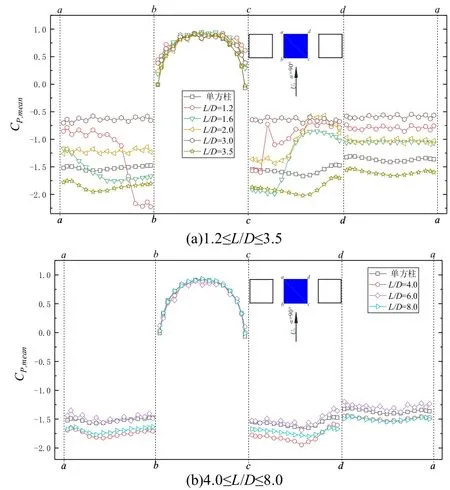
图12 90°风向角时中游方柱各测点的平均风压系数
图13 为α=90°时下游方柱的各测点平均风压系数.由图13(a)可知,当1.2≤L/D≤3.5 时,ab面各测点平均风压系数与上游方柱cd面的对称性良好;bc面从b点到c点,平均风压系数先增大后减小,与单方柱试验结果基本吻合;cd面从c点到d点与da面从d点到a点各测点平均风压系数变化并不明显.当1.2≤L/D≤2.0 时,各测点平均风压系数均为负值且绝对值小于单方柱试验结果,L/D=3.0和3.5时的平均风压系数接近单方柱试验结果.由图13(b)可知,当4.0≤L/D≤8.0 时,不同间距比下各测点平均风压系数变化情况基本一致,各面平均风压系数与单方柱试验结果接近.
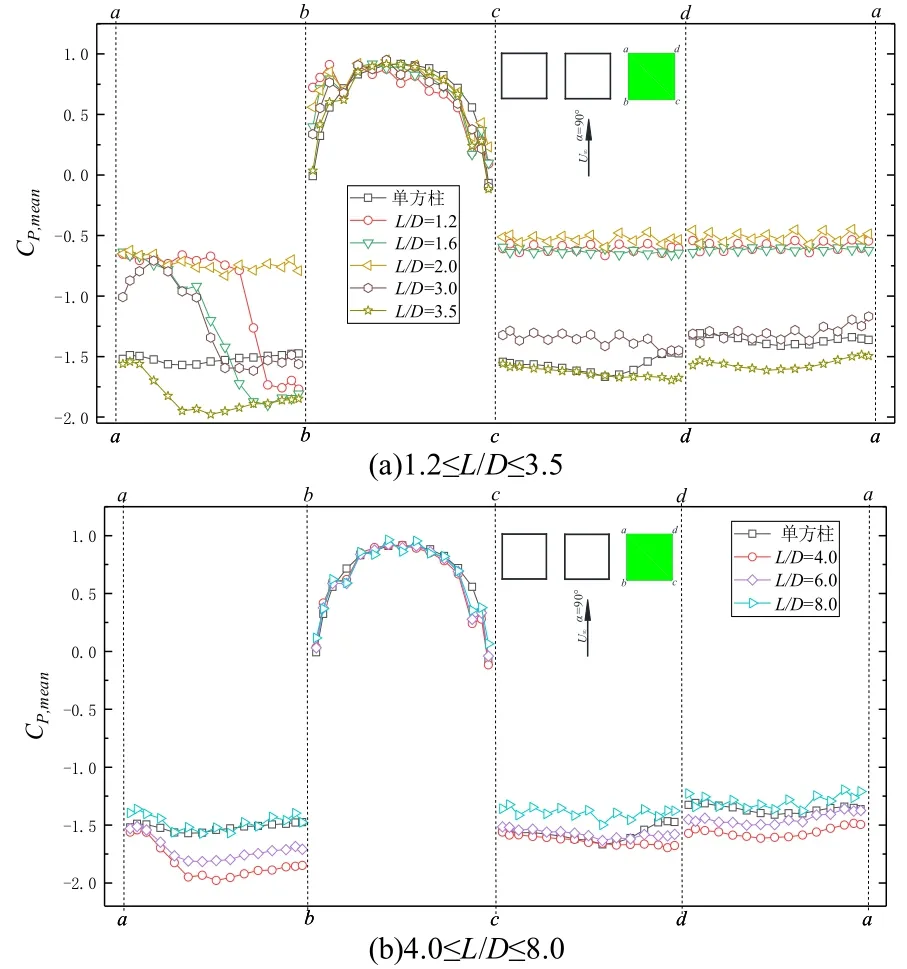
图13 90°风向角时下游方柱各测点的平均风压系数
3 结论
1)当1.2≤L/D≤3.5,且风向角较小时,不同间距比下的上游方柱各面均保持基本一致的风压分布,随着风向角的增大,干扰效应主要集中在cd面和da面;风向角的变化对中游方柱平均风压分布影响最为显著,且随着风向角的增大,干扰主要集中在ab面、cd面和da面;下游方柱所受到的平均风压干扰与中游方柱相似.
2)当4.0≤L/D≤8.0,且风向角较小时,上游方柱所受干扰与1.2≤L/D≤3.5 时相似,基本只受到较小的干扰效应;随着风向角的增大,上、中、下游方柱各面平均风压系数随间距比的增大逐渐接近单方柱试验结果.
