碰碰车与防撞梁正碰撞工况的瞬态动力学分析*

赵九峰

河南省特种设备安全检测研究院 郑州 450000

0 引言

碰碰车是碰碰车类游艺机中的一种可以任意行驶在固定车场内，依靠灵敏的转向系统，车体之间、车体与防撞梁不断发生碰撞的游乐设备。车架边缘配有起碰撞缓冲作用的缓冲胎，车场四周设有防撞梁，乘客驾驶碰碰车在车场内随心所欲的横冲直撞，从中得到极大乐趣。碰碰车的主要安全装置为安全带和缓冲胎，安全带主要防止乘客在游玩时，磕到方向盘上，缓冲胎可显著降低因为车辆相撞产生的惯性力，减轻过大惯性力对车体的损伤及给乘客带来的不适[1]。

以结构动力学理论为基础进行瞬态动力学分析，考虑碰撞体之间动量交换和惯性效应的前提下[2]，用以计算结构冲击或快速时变载荷下的结构动态响应，研究冲击载荷对设备结构的损伤状况[3]。车架和防撞梁作为碰碰车中经常受碰撞冲击部件，其强度计算一直是设计中的难点。碰碰车在运行过程中，经常承受作用时间很短但幅度很大的碰撞冲击载荷，传统的游乐设施结构计算中，采用1个放大冲击系数考虑碰撞冲击载荷的影响[4]，设计时一般无法准确计算；由于碰撞时间短、过程复杂，样机碰撞试验难以精确地测验碰撞过程中的受力变形[5]。为了解决当前碰碰车设计时碰撞冲击系数理论计算不精确，样机碰撞试验又过于昂贵和繁琐的现状[6]，以结构动力学理论为基础，应用有限元工程分析软件，模拟碰碰车和防撞梁的正碰撞过程，计算出碰撞过程中结构的最大应力分布情况，以确定碰撞载荷对车架和防撞梁结构强度的影响，并对计算结果进行安全分析与评价，可为碰碰车等游乐设施的产品设计提供参考。

1 碰碰车运行原理

碰碰车主要由车架、防撞系统、操纵系统、驱动系统、电控系统和电极板（地板）等组成。碰碰车前轮结构可360°旋转，且动力也在前轮上，结构简单、转向角度灵活。碰碰车的结构简图如图1所示。

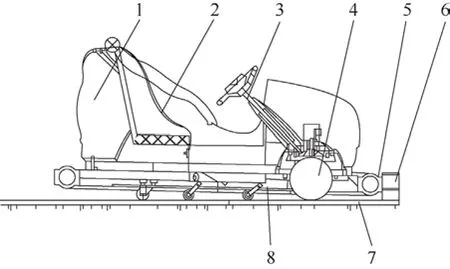
图1 碰碰车结构简图

碰碰车通过地板提供电力，可在整个地板上形成2极，因为在导电地板上有一系列带状，且碰碰车足够大，足以覆盖至少2个带状以形成完整电路。驱动系统采用直流电机驱动，通过车体上的导电轮使电机得电带动车体运行。碰碰车车架外侧四周配有橡胶做成的缓冲胎，运行碰撞过程中，撞击力通过缓冲胎间接作用在车架上，碰撞时起到缓冲作用，尽可能减少对车架的损伤和对驾驶人伤害[7]。

2 碰撞分析理论

碰撞分析通过动态接触问题来求解，碰撞冲击的问题属于典型瞬态动力学，是典型的连续接触力的非线性动态接触过程[8]，碰撞时系统满足动力分析方程

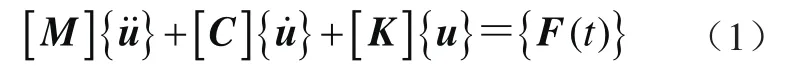
式中：[M]为结构质量矩阵，[C]为结构阻尼矩阵，[K]为结构刚度矩阵，｛｝为节点加速度向量，｛｝为节点速度向量，｛u｝为节点位移向量，｛F(t)｝为随时间变化载荷向量。

在任意给定的时间t，式（1）可看做是一系列考虑了惯性力［M］｛｝和阻尼力［C］｛｝的静力平衡方程。在Ansys程序中使用Newmark时间积分的方法，在离散的时间点上求解这些平衡方程。2个连续时间点之间的时间增量称为积分时间步长（Integration time step）。算法可以自动调节至适合的步长，使误差的估计逐渐趋于0，从而得到这种有效方法可靠的数值解[9]。

3 有限元分析

3.1 有限元模型

瞬态动力学分析可用来对承受碰撞冲击的结构进行动力响应过程中的载荷、强度模拟计算[10]。碰碰车运行时，碰碰车之间、碰碰车与场地防撞梁之间频繁地发生碰撞，车体结构和防撞梁经常受到冲击载荷作用，故有必要对其进行瞬态响应分析。

碰碰车满载时的总质量（含2名乘客）m=408 kg，碰碰车骨架为钢板（厚度t=2 mm），防撞梁为方管（100 mm×100 mm×2.5 mm）（长×宽×厚），材料为Q235B，碰碰车缓冲胎的材料为橡胶（厚度t=6 mm），碰碰车与防撞梁碰撞前的最大水平速度v=2.5 m/s。在建模、加载及求解过程中不考虑材料塑性影响，定义各部分的材料属性如表1所示。

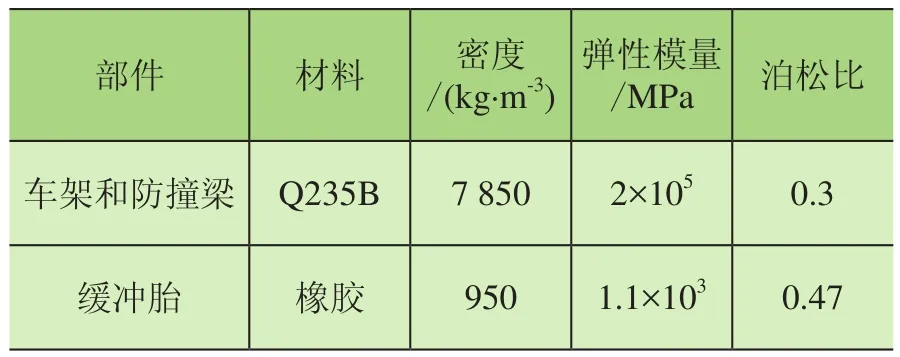
表1 材料的力学性能[11]

在Ansys Workbench瞬态动力学模块Transient Structural中对碰碰车骨架和防撞梁进行参数化建模和仿真分析。依据本次碰撞仿真的实验目的，为保证计算准确、减小计算规模并使模型能够反映碰碰车真实的力学特性，对碰碰车结构进行适当简化[12]，忽略碰碰车玻璃钢外壳、操纵系统、驱动轮等，在车架结构上附加质量单元（Point Mass）用来模拟乘客和座舱等质量。碰碰车和防撞梁的几何模型如图2a所示，采用4节点的壳单元Shell l81，每个节点拥有3个方向的平动自由度和3个方向的转动自由度，不仅能进行线性分析，还能应用于大应变、大转角状态下的非线性分析[13]。使用四边形为主的网格划分，在缓冲胎与防撞梁的可能接触部位，因碰撞接触产生应力，对网格进行细化，控制网格大小为10 mm，生成13 888个节点，14 151个单元。有限元模型如图2b所示。

图2 碰碰车和防撞梁模型

碰碰车缓冲胎与防撞梁之间施加面-面无摩擦接触（Frictionless），为了避免单元节点相互穿透，算法选择法向拉格朗日（Normal Lagrange），对于碰撞冲击类型、时间步控制选择预测碰撞（Predict For Impact）。对车架模型施加初速度2.5 m/s，车架底部施加Y向平动位移约束（Displacement），进行碰撞仿真分析，总分析时间为0.1 s。

3.2 结果分析

瞬态动力学分析求解碰碰车与防撞梁正碰撞的典型工况下的动态响应。碰碰车与防撞梁正碰撞的实质是缓冲胎与防撞梁接触的过程，碰碰车的冲击动能传递到防撞梁，再传递到防撞梁两端的固定约束部位，提取防撞梁约束位置的撞击力曲线[14]，如图3所示。

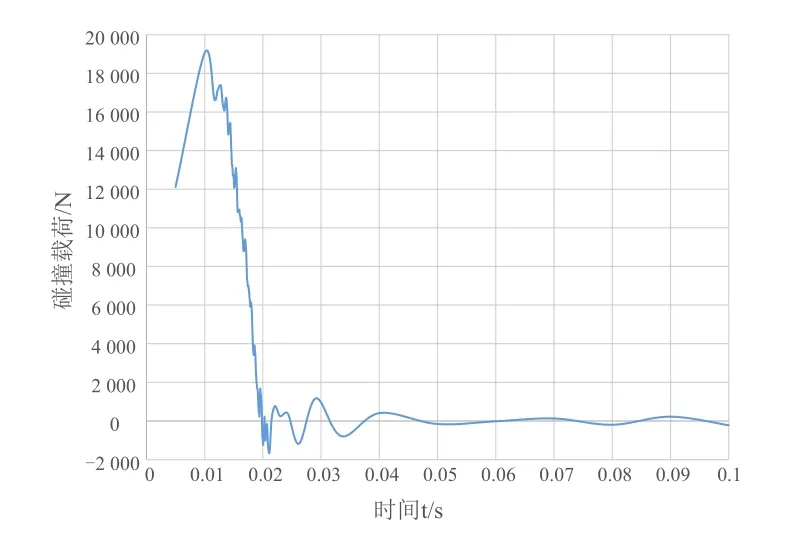
图3 撞击过程中接触力的时程曲线

由图3可以看出，碰碰车与防撞梁的碰撞载荷，在碰撞开始后10 ms达到峰值19 059 N，20 ms后碰撞结束，缓冲胎与防撞梁脱离接触。碰撞载荷经过较短一段时间波动后趋于0。

碰碰车防撞梁的分析结果如图4所示。碰撞过程中防撞梁的最大应力时间历程曲线如图4a所示。图中可以看出，在0.01 s时，防撞梁应力达到最大峰值，提取此刻防撞梁的应力云图如图4b所示，防撞梁的最大应力为73.981 MPa，出现在防撞梁碰撞接触位置。

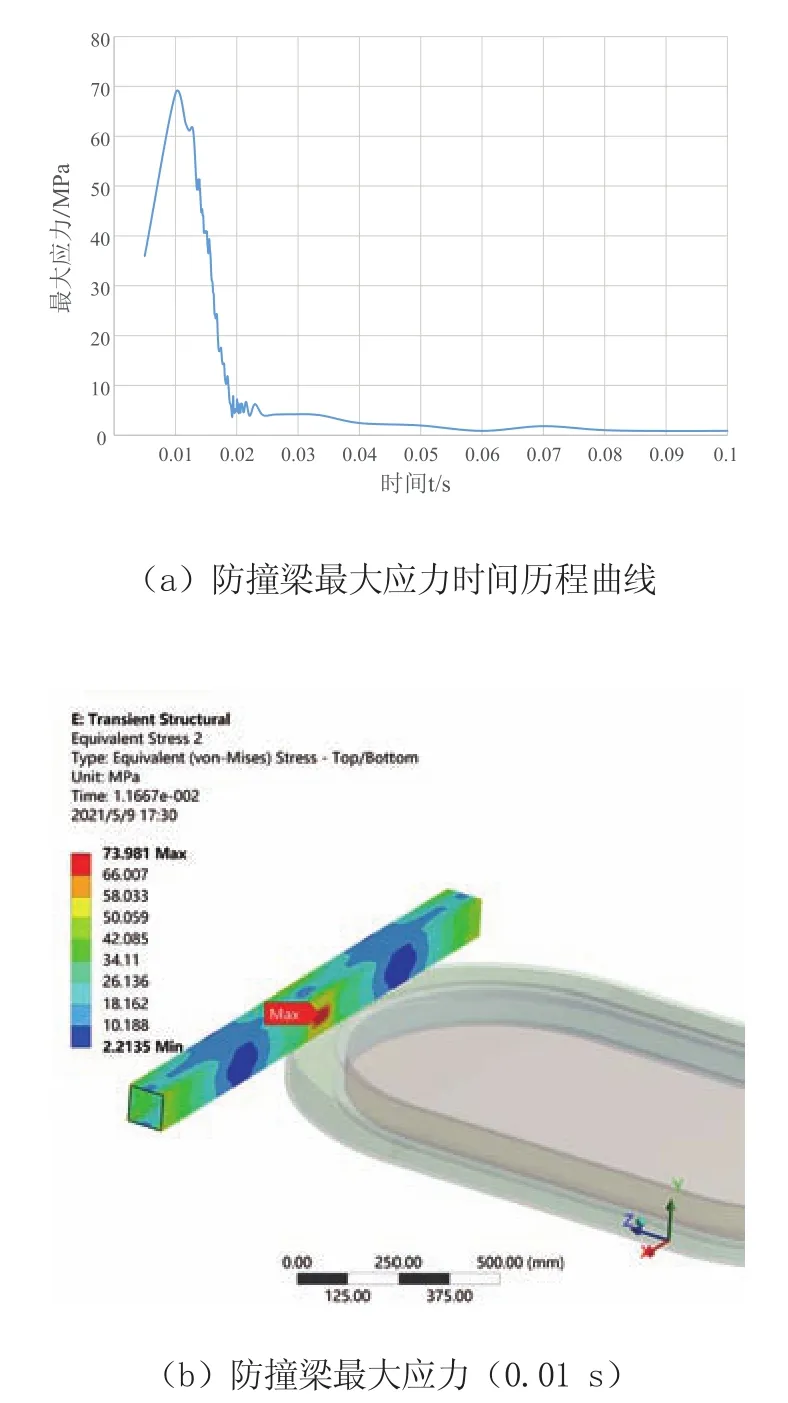
图4 防撞梁分析结果

碰碰车车架的计算结果如图5所示。碰撞过程中车架的最大应力时间历程曲线如图5a所示。图中可以看出，在0.01 s时，车架应力达到最大峰值，提取此刻车架的应力云图如图5b所示，车架的最大应力为68.52 MPa，出现在车架前方位置。

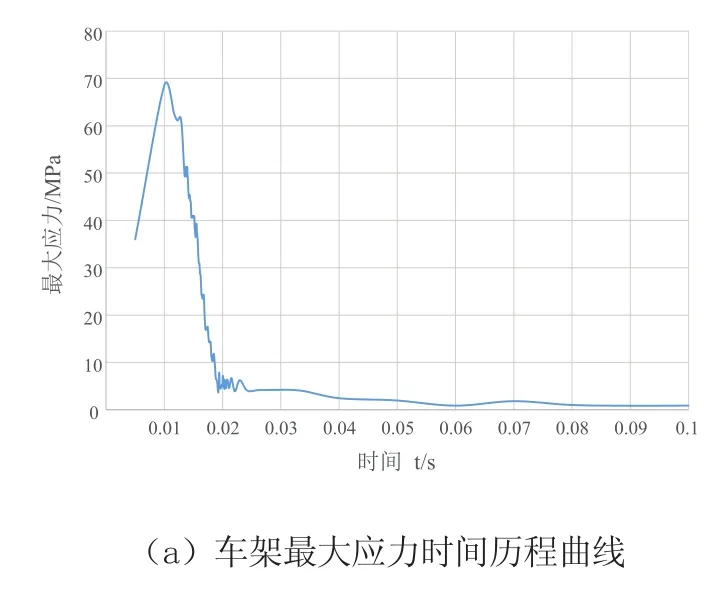
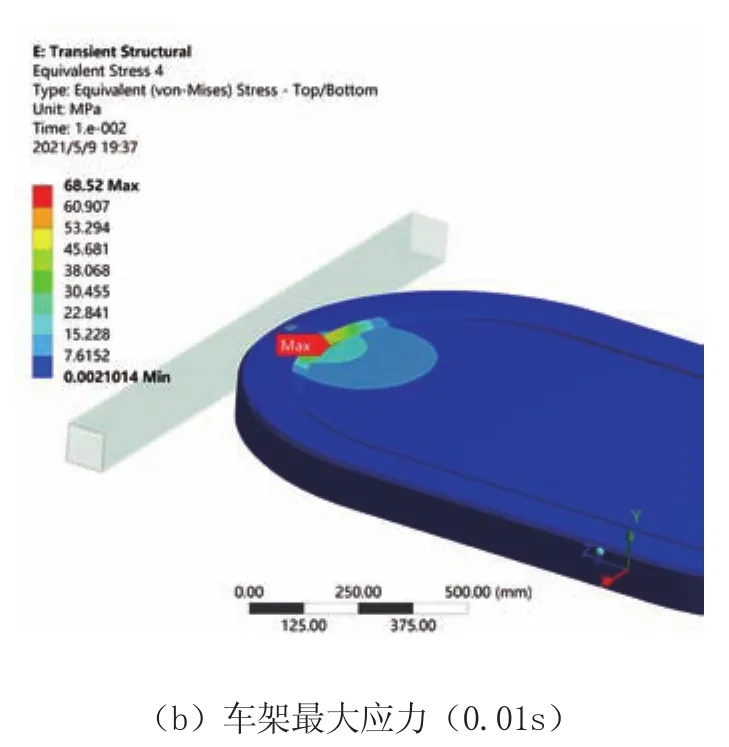
图5 车架分析结果e（0.01s）

4 安全评价

由GB 8408—2018《大型游乐设施安全规范》6.2.2条：材料极限应力与其承受的最大应力的比值为安全系数，运动部件和不直接涉及人身安全的支撑框架安全系数n≥3.5[15]。故游乐设备中零部件的安全系数

式中：bσ为材料的极限应力，Q235B材料bσ＝375 MPa。

由式（2）可得，防撞梁的安全系数n＝375÷73.981＝5.1；车架的安全系数n＝375÷68.52＝5.5。碰碰车防撞梁和车架的安全系数大于3.5，满足使用要求。

5 结论

本文以碰碰车为工程背景，运用有限元软件Ansys Workbench的瞬态动力学分析模块对碰碰车进行碰撞冲击模拟计算，模拟碰碰车与防撞梁正碰撞的动力学特性，获取传统力学理论计算无法或难以计算得到的数据，并依据分析结果对结构安全进行评价校核，计算结果表明：

1）通过碰碰车车架与防撞梁正碰撞工况下的瞬态动力学分析，提取各部件的应力时程曲线，能获取整个碰撞过程中设备的薄弱部位，为进一步的结构改进设计提供参考设计提供参考。

2）由分析计算结果，依据相应的规范标准，对碰碰车车架和防撞梁进行安全校核与评价，碰碰车车架和防撞梁的安全系数大于3.5，计算结果表明车架和防撞梁满足设计要求。

3）建立碰碰车和防撞梁的模型并进行了仿真分析，其建模方法也适合其他游乐设施的仿真分析，对于碰撞性能的仿真结果，还需要结合实车样机试验验证并深入研究。

瞬态动力学分析方法可在设备动态碰撞冲击仿真过程中，实时输出关键部位的在整个碰撞过程中的动应力曲线，获取任意一点在任意时刻的应力值，也可以得到某一时刻的应力分布，从而保证计算结果的准确性和可靠性，提高计算的效率。