基于区间分析的汽车起重机结构非概率可靠性研究*
2021-12-21莫光辉田国富
莫光辉 王 涛 田国富
沈阳工业大学机械工程学院 沈阳 110870
0 引言
汽车起重机是现代工业中不可缺少的设备,它在很大程度上减轻了劳动强度,其安全问题随之受到高度重视。臂架作为汽车起重机的主要承载结构,其安全性决定着整机的安全性。传统可靠性求解方法为概率论和模糊理论描述不确定变量,概率论法和模糊理论需要获知详细的数据信息,而汽车起重机的生产批量小,不能收集到足够的数据,容易得到不确定因素的界限。
Ben Haim Y 等[1]于1994年第一个提出基于凸集合模型的非概率可靠性理论;Ben-Haim Y 等[2]根据非概率可靠度定义研究结构的非概率可靠性,认为非概率可靠性指标是一个区间;郭书祥等[3]将结构的不确定参数描述成区间变量,使用非概率可靠性理论进行了结构可靠性研究;王欣等[4]对轮式起重机的箱形臂架进行了非概率可靠性优化;王睿星等[5]对4种主要的结构非概率可靠性模型进行了比较;杨淑伟等[6]首次对起重机臂架结构进行了凸模型非概率可靠性分析;刘丽等[7]对履带式起重机进行了区间非概率可靠性分析。
由于汽车起重机臂架区间非概率的研究不多,本文将汽车起重机的起升载荷、冲击系数、偏摆角作为载荷的不确定性,确定臂架结构强度、刚度、稳定性可靠性计算准则,建立区间非概率可靠性模型,并用工程实例来验证其正确性。
1 区间分析方法
1.1 区间分析的基本概念
不确定变量a为有界限的变量,其上界限为a1,下界限为a2,满足a∈A=[a1,a2](A为总向量集合)称a为区间变量。通过标准化转化有
式中:ac为a的均值,ar为a的离差,δ为标准化区间变量取值为[-1,1]。
1.2 非概率可靠性分析方法
设向量X=(x1,x2,…,xn)为与结构相关的基本区间变量集合,xi∈X(i=1,2,…,n)。取M=g(X)=g(x1,x2,…,xn)为结构的功能函数。设其均值用Mc表示,离差用Mr表示,结构的非概率可靠性为η=Mc/Mr。由结构可靠性理论可知,超曲线g(X)=0表示失效面,结构的基本参数空间被失效面分为失效域与安全域2部分,当M=g(X)<0时结构属于失效的,当M=g(X)>0时结构属于安全的。

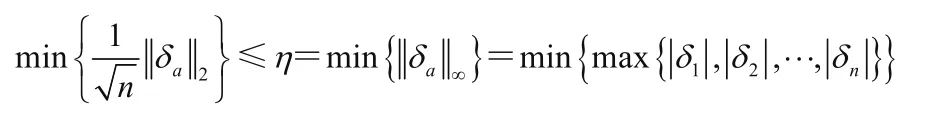
只有在g(δ1,δ2,…,δn)=0和|δ1|=|δ2|=…=|δn|时等式才成立。
2 汽车起重机臂架结构非概率可靠性
2.1 臂架结构区间变量及运算
本文将臂架中存在的额定起升载荷Q、起升冲击系数φ1,起升载荷的偏摆角φ作为不确定量,用区间表示为Q∈[Ql,Qu]、φ∈[φl,φu]、φ∈[φl,φu]可根据区间均值和离差公式求出这3个不确定区间变量的均值和离差分别为Qc、Qr、φc、φr、φ1c、φ1r,然后进行标准化变换得到

本文中相关的区间变量所受力和力矩标准化公式为

式中:δ1、δ2、δ3、δ4为相应变量的标准化区间变量值。
2.2 臂架的整体非概率稳定性功能函数
臂架整体稳定性失效准则确定的功能函数为
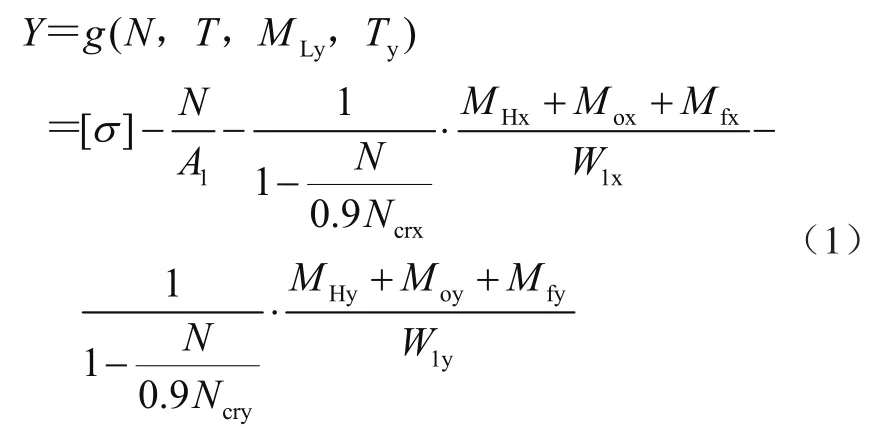
式中:[σ]为许用应力,A1为基本臂截面积,W1x、W1y为基本臂抗弯模量,Ncrx、Ncry为变幅回转平面的临界力,MOx、MOy为臂架端部弯矩,MHx、MHy为横向载荷在变幅回转平面的最大弯矩,Mfx、Mfy臂架间隙挠度产生的弯矩。
由式(1)可得
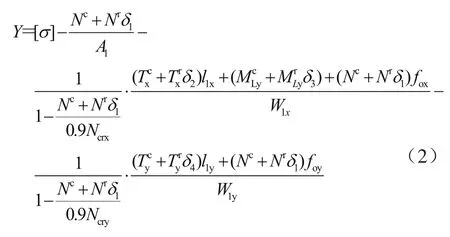
非概率可靠性指标定义为

2.3 臂架强度非概率可靠性功能函数
臂架z处的强度非概率可靠性功能函数为
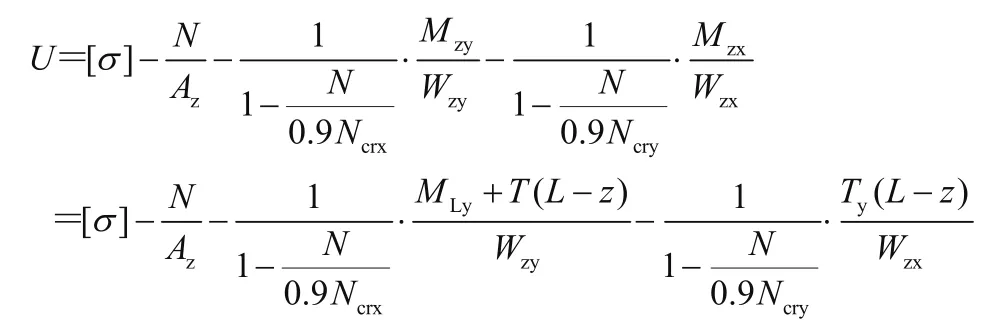
式中:Mzy、Mzx为横向载荷在变幅回转平面产生的截面弯矩,Wzy、Wzx为断面抗弯模量。
结合上式可得

非概率可靠性指标定义为


2.4 臂架的刚度非概率可靠性功能函数
臂架在变幅平面的刚度非概率可靠性功能函数为

回转平面的刚度非概率可靠性功能函数为

3 工程实例
对某25 t汽车起重机臂架进行可靠性分析,选取得起重机臂架总长L=32 400 mm,臂架材料为HG60钢,屈服强度σs=460 MPa,抗拉强度σb=570 MPa,计算选择最危险的工况,伸缩臂全伸,臂架幅度为5.5 m,起升角度为θ=81º,额定起升载荷为6 t。起重量的变化区间为Q∈[50,60] kN,起升冲击系数φ1∈ [0.85,1.15],偏摆角φ∈ [2º,5º],根据公式可以得到轴向力F∈[102.2,119.7] kN,横向力Tx∈[12,13.8] kN,载荷偏心引起的弯矩MLy∈ [2.3×107,2.9×107] N · mm,回转平面所受的侧向载荷Ty∈[2.7,6] kN。计算参数如表1所示。

表1 臂架主臂截面性质
将实例中区间变量标准化,即有
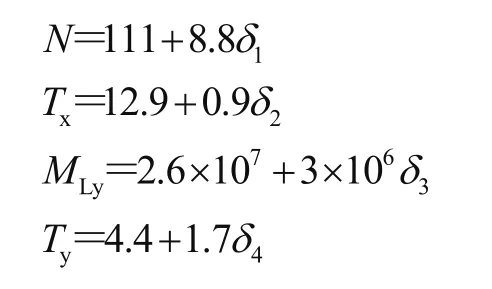
3.1 臂架的稳定性非概率可靠性计算
在此工况下,n=1.33,则许用应力为

将表中1数据带进来得到结果,令Y=0,得到η1=1.6669 07>1,可知道此臂架得整体稳定性是可靠的。
3.2 臂架的强度非概率可靠性计算
由臂架强度失效准则可知,以往的力学分析和臂架受力特点可选取每节臂的搭接处截面和第一节臂与变幅液压缸的交点处截面为最危险截面进行臂架强度失效分析(见图1),臂架计算截面参数见表2。

表2 臂架计算截面参数
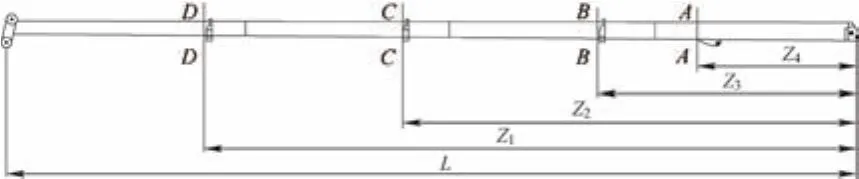
图1 臂架强度危险截面
将相应的数据带到式(3)可得:ηA=1.854 1,ηB=1.644 9,ηC=1.457 5,ηD=2.377 5。由计算结果可知,该臂架的强度非概率可靠性是安全的。
3.3 臂架的刚度非概率可靠性计算
臂架的刚度非概率可靠性计算公式为

臂架计算长度参数为:L=32 400 mm,L1=9 728 mm,L2=9 628 mm,L3=9 159 mm,L4=9 170 mm,H1= 26 400 mm,H2= 22 672 mm,H3= 15 152 mm,H4=7 653 mm,l1=5 270 mm,l2= 2 108 mm,l3=1 660 mm,l4=1 517 mm。将以上参数代入到功能函数公式中,即可得出变幅平面刚度非概率可靠度为η2=1.146 3,回转平面刚度非概率可靠度为η3=1.205 1,由此可知该臂架满足整体的刚度稳定性。
4 结论
1)由区间非概率可靠性方法对工程实例进行计算得出臂架的稳定性、强度、刚度可靠性结果均大于1,可知该臂架结构处于安全状态,用此方法只需知道不定量参数的集合界限,而无需知道大量样本信息弥补了缺少实验数据的问题,对臂件的内部结构无要求。
2)由对工程实例的计算可知,用区间非概率可靠性的方法计算汽车起重机可靠性问题只需知道额定起重量、起升冲击系数、起升载荷偏摆角度这些不确定量的区间,就可计算出结构的可靠性指标。
