基于综合赋权和改进集对分析的起重机安全评价

王建儿 邝湘宁 仇佳捷 杨金辉 张 芳

宁波市特种设备检验研究院 宁波 315000

0 引言

我国现存起重机数量庞大，大多数因长期使用而运行性能受到较大影响。起重机安全问题自2014年起逐渐增多，2016年发生的起重机安全事件达94起[1]。起重机在工业生产中处于重要地位，保障其安全运行意义重大，对起重机进行安全评价能预防安全事故的发生，进而确保起重机的安全工作。

现有的起重机安全评价方法有综合安全评判法、模糊层次分析法（FAHP）、基于灰度理论的评价方法、基于组合赋权的评价方法、基于未确知测度理论的评价方法、人工神经网络、支持向量机（SVM）、基于可拓理论的评价方法等。Stian R等[2]综合了风险分析和成本效益并应用于起重机安全评价；胡静波等[3]研究人员采用模糊层次综合分析法评价门式、桥式起重机安全等级，实现了起重机的定量分析评价；陈兆芳等[4]将灰色理论和层次分析法结合并应用于门座起重机门架系统的安全评价，优化了评价时间，提高了评价结果的客观性；Li A H等[5，6]研究出一种结合熵权和累积前景理论的起重机安全评估模型，该模型根据综合远景值的排序来确定安全等级，后续研究出基于正态隶属度函数的变量模糊集评价模型，用于评价岸边集装箱起重机的安全等级。朱思明等[7]将12台起重机测得信息和寿命评价数据对LM-BP神经网络进行训练，拟合出起重机评价模型；舒文杰等[8]量化处理了起重机检测数据，并通过主成分分析法降维，采用支持向量机构建桥式起重机安全评价体系；赵晓姣等[9]将可拓理论和改进层次分析法结合，为起重机安全评价提供了一种新的方法。由于起重机设备的特殊性，其正常运作依靠多种因素协同配合来实现，而上述评价方法具有一定局限性，影响最终的评价结果。现有方法在求解指标权重上大多使用单一指标权重或人为因素影响较大的组合权重，难以保证评价结果的客观性。本文基于综合赋权和改进集对分析理论构建起重机的安全评价模型，分别采用熵权法和CRITIC法求解指标权重，使用博弈论方法组合2组权重，得出起重机安全评价的组合权重，采用改进的集对分析理论对起重机安全进行评价。运用该评价模型对通用桥式起重机进行评价，证明了综合赋权和集对分析理论在起重机安全评价中合理性与有效性。

1 指标权重的计算

桥式起重机安全评价流程包含构建指标体系、计算综合权重和评价结果3部分，如图1所示。

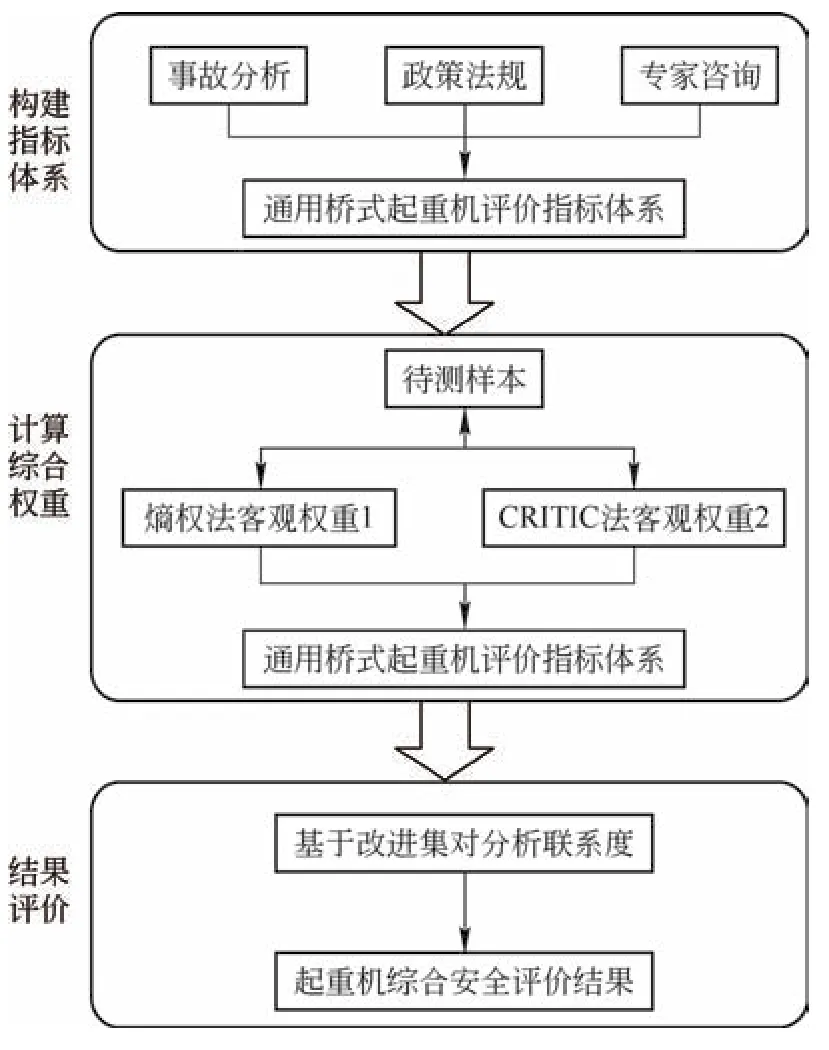
图1 桥式起重机安全评价流程图

1.1 熵权法

信息熵最早由香农在1948年提出[10]，熵权法通过事物具备的信息量计算指标权重，信息量越大指标权重越大，相反则指标权重越小。熵权法通过结合样本值使各指标权重客观性较强,熵权法的具体步骤是先构建评价矩阵，然后确定指标权重。

1）构建评价矩阵

假设共有p个待评价样本，单个待评价样本共有m个评价标，则样本i的第j个评价指标的评价值为µij（i＝1，2，…，p；j＝1，2，…，m），各样本指标评价值组成的评价矩阵U＝(dij)p×n为

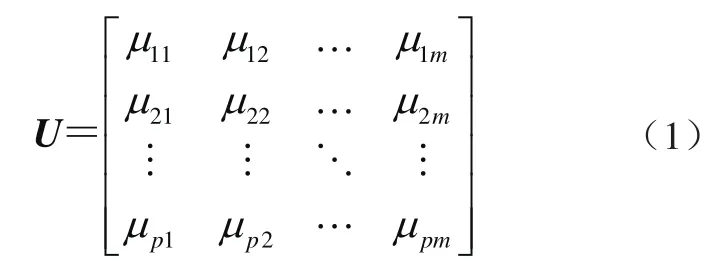
2）指标权重确定

假设每个评价指标共有n个等级，则第j个评价指标的信息熵为

式中：pjk为评价指标在对应等级的概率，当pjk＝0时，pjklnpjk＝0，以使公式有意义。

则第j个评价指标的熵权为

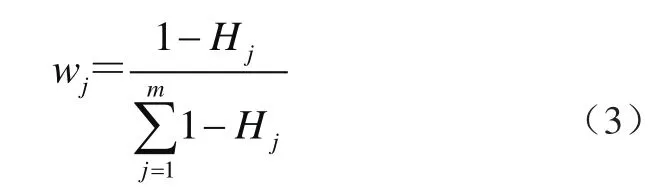
评价指标的权重向量为

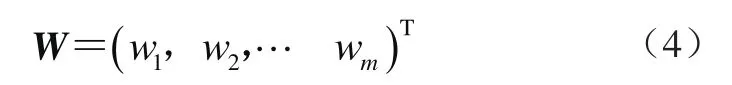
1.2 CRITIC赋权法

Diakoulaki在1995年提出名为CRITIC的客观赋权方法[11]，通过引入待评价样本的对比强度和冲突性使权重结果客观性更强。其中，对比强度即评价指标间的区别通过标准差来体现，标准差的数值越大，评价指标包含的信息量越大；冲突性体现了指标间的联系度，2指标间的联系度越小则冲突性越大。评价矩阵与式（1）相同，CRITIC赋权法的求解过程是进行评价指标归一化处理，得出评价指标均值和标准差，然后计算相关系数和客观权重。

1）评价指标归一化处理

对越大越优的指标为

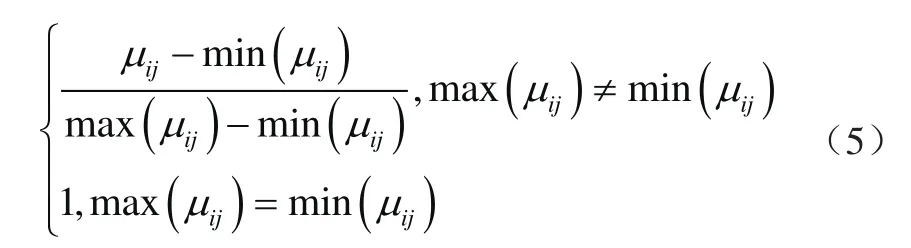
对越小越优的指标为

2）评价指标均值和标准差

式中：为p个样本评价指标µj的平均值，σj为评价指标µj的标准差。

3）计算相关系数

指标间的联系程度通过评价指标的相关系数体现。相关系数按照积差的方法计算，以2种评价指标评价值与各指标平均值的离差为基础，由2种指标的离差相乘来表示指标间的联系度，即

式中：rij为指标Xi和Xj的相关系数。

4）计算客观权重

由上述公式求解的标准差和相关系数可得到指标包含的信息量为

计算第j个评价指标的客观权重为

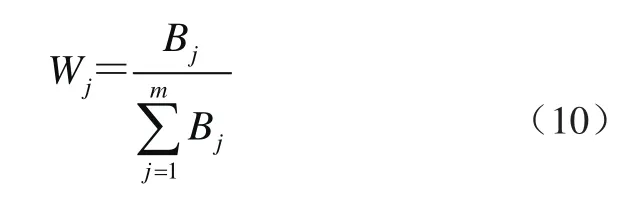
1.3 基于博弈论的综合权重

博弈论综合各类权重的方法在于组合后的权重与各类权重的偏差最小[12]。通过熵权法和CRITIC赋权法求解的2类指标权重，即本文使用2种方法求解基本权重，从而获得2个权重向量W(l) ＝(wl1，wl2，…，wlm)，l＝1、2，则2个权重向量的任意线性组合为

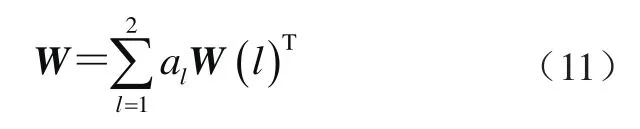
式中：al为线性组合的系数，W为组合权重向量。

为综合考虑2类权重值，通过W与W(l)的离差最小化为优化目标，求解组合系数al，得到最优组合矩阵W，优化过程的目标函数为

根据矩阵的微分性质，式（12）的最优化一阶导数可等价为

根据式（13）求得组合系数向量(a1，a2)，归一化处理向量中元素

由博弈论求解评价指标的综合权重为

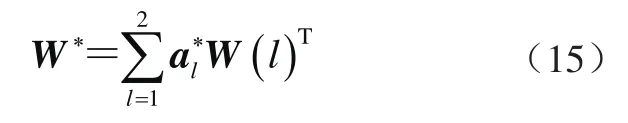
2 集对分析理论评价模型

2.1 桥式起重机评价指标与评价标准

桥式起重机安全问题的种类繁多，结合国内外桥式起重机发生安全问题的原因，经过专家分析确定4个一级评价指标分别为桥架B1、起升机构B2、运行机构B3、人及安全因素B4，提取16项二级评价指标分别为结构连接C1、裂纹变形C2等，如图2所示。评价标准可确定为I级（优）、II级（良）、III级（中）、IV（较差）、V（差）5个等级，对通用桥式起重机5个等级的分级界限值进行标准化转换，各指标对应的等级范围标准化结果如表1所示。

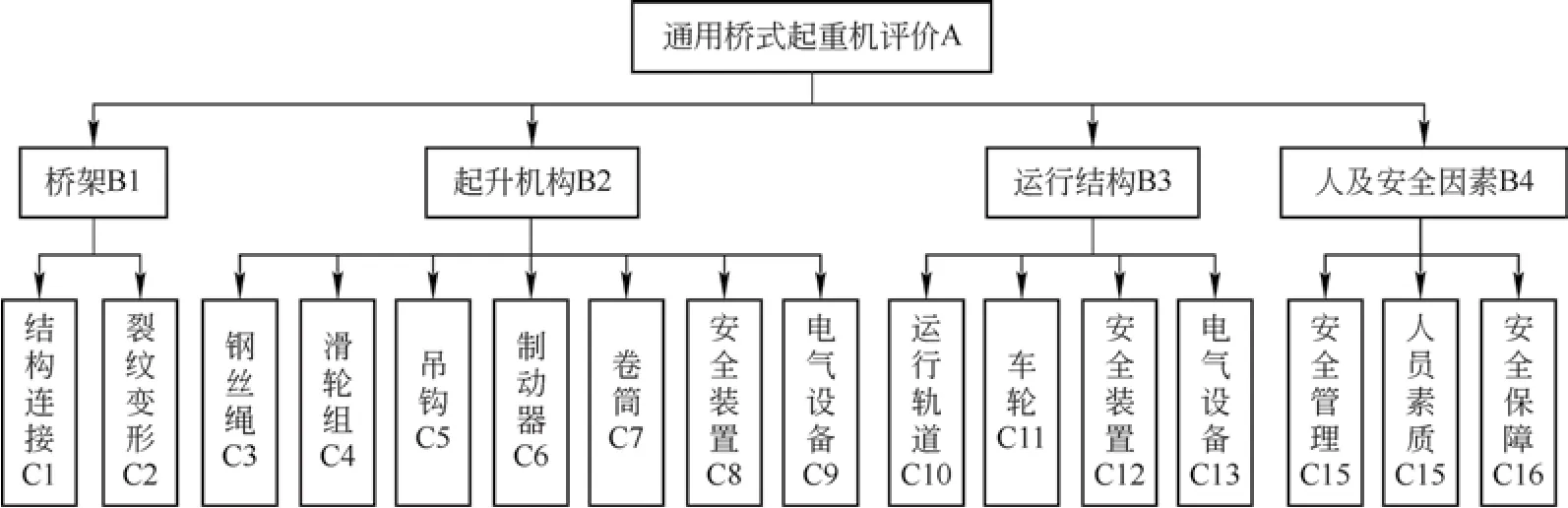
图2 通用桥式起重机评价指标体系

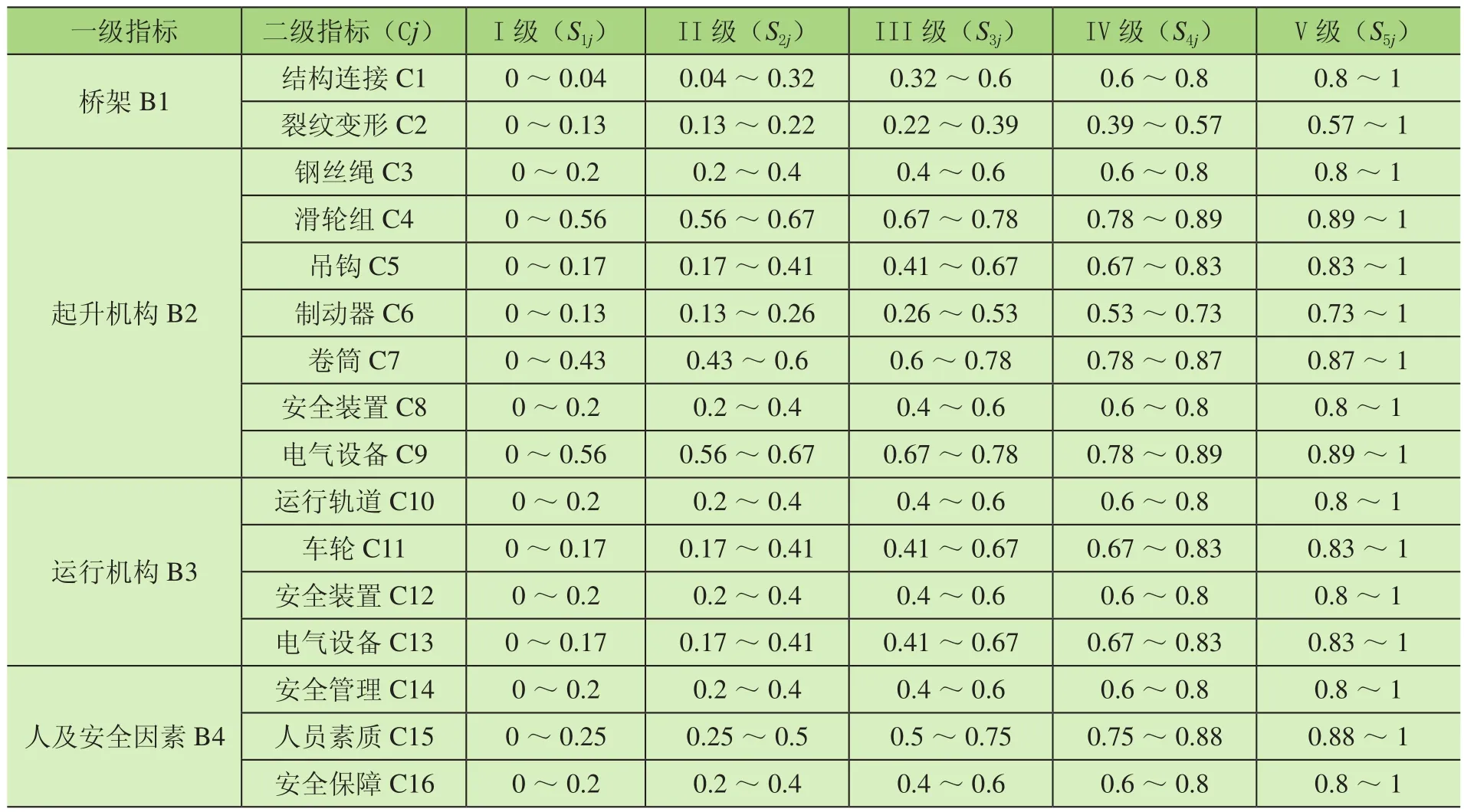
表1 通用桥式起重机评价指标及分级标准化处理

2.2 改进集对分析评价模型

赵克勤于1989年提出的一种用于解决不确定性模糊问题的分析方法，叫作集对分析理论[13]，现如今广泛应用于电能质量、交通管制、水资源承载力的评价等领域。集对分析理论的原理是将评价样本和影响因素之间的关系看作一种不确定性系统，2个影响因素之间存在相同、差异和对立3种关系性质，其中相同性、对立性属于确定性关系，差异性属于不确定性关系。集对分析理论不仅具备传统解决不确定问题方法的优势，同样能客观地考虑影响因素间的关联性，实现更合理客观的评价。

传统集对分析的基本原理为：假设A集合、B集合构成集对H＝（A，B），在待评价样本的基础上分析集对H，A集合、B集合总共存在N个因素，相同性因素有S个，对立的因素有P个，差异性因素有F个，则2集合的联系度为

式中：λ为2集合的联系度；i为差异性系数，取值范围[-1，1]；j为对立性系数，j＝-1；a、b、c分别为同一度、差异度和对立度，a、b、c的取值范围为[0，1]，三者满足条件a+b+c＝1。

传统集对分析理论应用于评价方案时，具备以下特点：待评价样本的样本值位于某评价级别范围内时，则认定两者同一；样本值位于相隔等级范围内，即认定2样本对立；样本值位于相邻等级范围内，即认定两者差异。但是，这种关系评定方法过于笼统，无法应对特殊情况如样本值位于等级边界。对传统集对分析评价方法进行改进，对于样本i的指标j的评价值µij，Skj为指标j的等级k的界限值（k＝1,2,…,5；j＝1,2,…,16）。当µij位于Skj的相邻等级中，若更接近等级的优良一侧则认定为优异，设为b1；若更趋于较差一侧即认定为劣异，设为b2。当µij位于Skj的相隔等级中，若更接近等级的优良一边则认定为优反，设为c1；若更接近劣差一侧即认定为劣反，设为c2；拓展后联系度方程可表示为

式中：i1∈[0，1]，i2∈[-1，0]，j1∈{0，1}，j2＝-1，系数满足a+b1+b2+c1+c2＝1。

根据评价值与各等级取值范围的距离计算系数。若评价值位于评价等级中，则a＝1，其余系数为零；当样本值位于相邻级别中，距离该级别边界越近，a值越大，相反则b1、b2、c1、c2值越大；距离相邻等级优良一侧越远，a值越小b1值越大，相反则a值越大b1值越小；若距离相邻等级较差一侧越远，a值越大b1值越小，相反则a值越小b1值越大；若样本值位于相隔等级中，若距离该等级优良一侧越远，则a和b1值越小，c1值越大；若距离劣差一侧越近，则a和b2值越大，c2值越小。结合改进集对分析模型求解指标j的5个级别的联度可为

2.3 起重机安全评价等级的确定

采用改进后的集对分析理论评价起重机的安全等级，即将安全程度和评价等级形成1个集对，求解待测样本的评价指标j和各评价等级n的联系度µnj，通过上述求得的综合权重，得到平均联系度

式中：µn为评价指标与评价等级n的平均联系度，wj为评价指标的权重。若µc＝max{µn}，c＝（1，2，…，5），则样本评价等级为c级。

3 通用桥式起重机案例分析

3.1 评价值来源与预处理

以桥式起重机为研究对象，根据文献[9]中4台通用桥式起重机各评价指标的评价值，对样本值进行归一化处理，整理的评价值如表2所示。

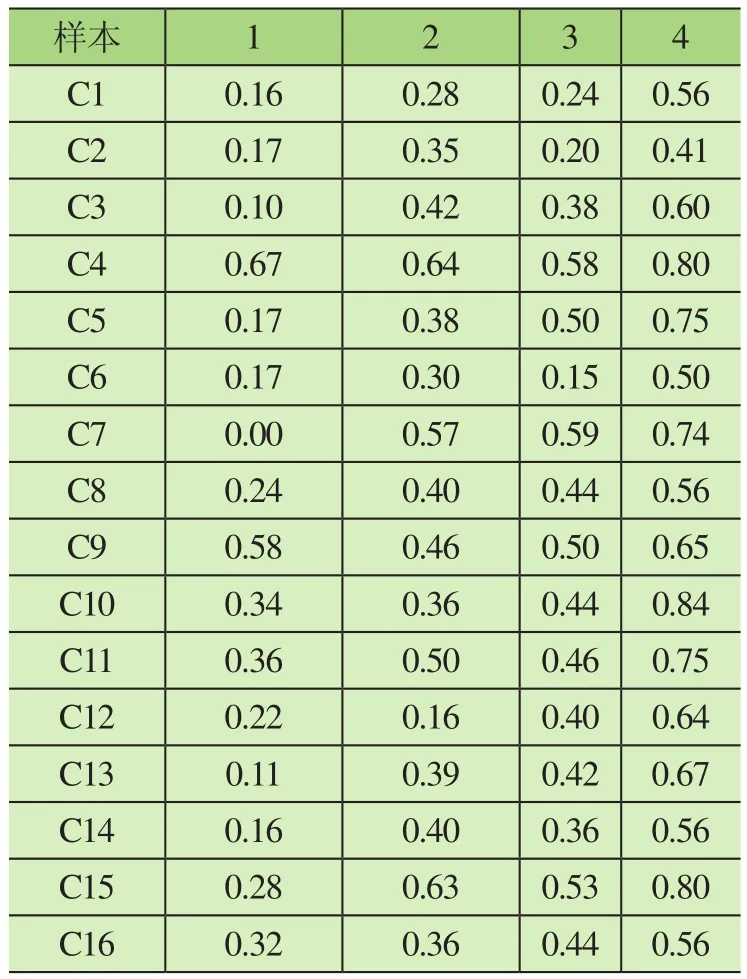
表2 4台通用桥式起重机评价值

3.2 评价指标的权重

根据4台通用桥式起重机的评价值，分别由熵权法和CRITIC法求解评价指标权重。其中，熵权法指标权重w1由式（1）～式（4）求解，CRITIC法指标权重w2由式（5）～式（10）求解，最后通过博弈论组合权重法式（11）～式（14）求解综合赋权系数并归一化处理，求出，通过式（15）求解出评价指标的综合权重w*，3种权重的计算结果见表3。

表3 评价指标权重

3.3 评价指标的联系度计算

结合表2中4台起重机评价指标的标准样本值，通过式（17）～式（21）分别计算样本各评价指标对应评价等级I级～V级的单指标联系度λ1～λ5，因篇幅限制，此处仅列举第一台起重机的联系度矩阵λX1。

3.4 通用桥式起重机综合安全评价

通用桥式起重机的安全评价综合了多个指标的特性，而前述仅求解了样本的单指标等级联系度，无法整体评价起重机的安全等级。结合式（23）的平均联系度函数和前述求解的综合权重值，求得起重机样本1～4的指标等级平均联系度矩阵为

基于均分原理[14]，令i1＝0.5，i2＝-0.5，j1＝0，j2＝-1，将系数值代入各样本平均联系度矩阵，得出表4所示各样本所有评价等级联系度和综合评价等级。

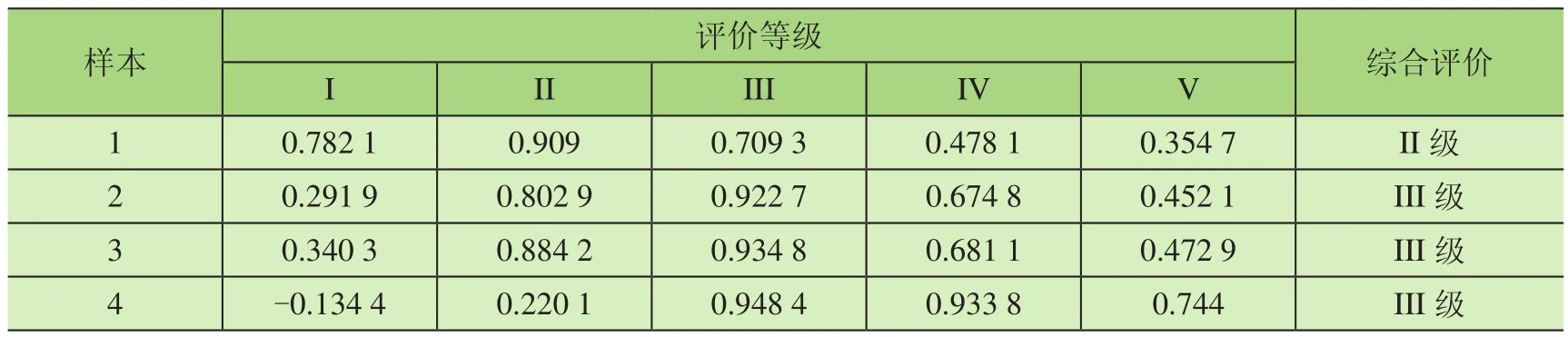
表4 综合评价结果

根据表4计算结果得出，样本1的评价指标中有4项指标为I级，11项指标为II级，1项指标为III级；起升机构中的评价指标滑轮组C4表现较差，需要在后期及时更换滑轮组。样本2的指标中存在2项指标为I级，7项指标为II级，7项指标为III级，表现为III级的主要为桥架中的裂纹变形；起升机构中的钢丝绳、制动器、安全装置，运行结构中的车轮、人及安全因素中的安全管理和人员素质，其中钢丝绳在安全评价中权重较大，需要格外关注，定时检修和更换。样本3的指标中有1项为I级，7项为II级，8项为III级，表现为III级的评价指标中运行机构的安全装置需要格外关注。样本4的指标中有1项为II级，7项为III级，7项为IV级，1项为V级，表现最差的为运行机构的运行轨道，需要立即更换，避免发生安全事故。

4 结论

桥式起重机作为一种大量在仓库、码头、厂房工作的特种设备，其安全状况对安全生产起到关键作用。本文首先将客观权重求解方法熵权法和CRITIC法求解指标权重并通过引入博弈论将2组权重合理综合，采用改进集对分析理论求解样本与评价等级之间的联系度，得出通用桥式起重机的安全评价模型，对4台起重机样本进行安全等级评价。

1）设置的评价等级全面考虑了桥式起重机的主要影响因素。将博弈论思想综合熵权法和CRITIC法求解的权重，既避免了主观赋权的误差，又较大程度保留了2种权重方法的优势。

2）通过改进集对分析理论构建通用桥式起重机安全评价模型有效地解决了综合评价中的不确定因素，更直观地得到评价指标与评价结果的联系度。

3）运用该安全评价模型得出样本1为II级，样本2、3、4为III级。由4台起重机的联系度矩阵可知，在起重机的工作过程中，易损耗类的构件如滑轮组、钢丝绳、运行轨道需要格外关注，定时地检修更换，保障起重机安全稳定地运行。