建筑结构化爆作用级数型荷载动力系数研究
2021-12-20耿少波贺耀北
刘 榕,耿少波,贺耀北,3
(1.湖南省交通规划勘察设计院有限公司,长沙 410200;2.中北大学 土木工程学科部,太原 030051;3.湖南大学 土木工程学院,长沙 410082)
重要的建筑物一般需进行抗爆设计,爆炸荷载作为一种偶然作用,常分为核爆、化爆和物理爆炸三类。和平与发展仍为当今时代发展主题,且受世界范围内核材料的严格管控,核爆发生概率很低。我国大量危险性化工企业、工矿企业逐步被城市包围,遍布的燃气管网、加油加气站、储油储气站及烟花爆炸储运等重大爆炸危险源的大量增加,建筑结构遭受化爆作用发生灾害现象呈上升趋势,例如2019年江苏盐城化工厂爆炸事故造成严重后果。同时,受国际政治变化、民族冲突、恐怖袭击等不稳定社会影响,选择建筑结构进行常规武器爆炸袭击的可能性也在增加,例如2015年我国驻索马里使馆遭受炸弹袭击受到国际社会强烈关注。
国外进行建筑结构抗爆设计研究较早,并形成了相关设计手册或指南,例如美国的技术手册TM5-1300《抗偶然爆炸结构设计手册》[1]、TM5-855-1《常规武器防护设计原理》[2]、UFC 3-340-02[3]和加拿大的CSA/S850-12[4]。我国民用抗爆设计主要在人防工程领域,现已形成国标GB 50038—2005《人民防空地下室设计规范》[5],轨道交通领域RFJ 02—2009《轨道交通工程人民防空设计规范》,北京市DB 11/994—2013《平战结合人民防空工程设计规范》。2012年修订的GB 50009—2012《建筑结构荷载规范》[6]中也新增了常规武器爆炸作用的计算方法及说明。爆炸荷载结构响应涉及流固耦合、几何及材料非线性等计算内容,计算效率很低,不利于结构抗爆设计。因此,与国外抗爆设计规范类似,我国现行规范在结构抗常规武器等化爆作用设计时,建议采用动力系数进行等效静力荷载换算,实现基于构件层次的结构抗爆设计。现行规范将爆炸荷载简化为正超压作用下等冲量线性衰减模式。动力系数需要由等效单自由体系弹塑性振动响应得出,该振动方程为二阶常系数微分方程,荷载简化后使得方程求解容易,因此该简化模型得到了国内外规范广泛认可。
在研究领域,Biggs[7]较早采用线性衰减荷载等效单自由度法对无阻尼简支梁、固端梁、简支-固端梁及双向板等进行了等效静载分析,并形成了动力系数的近似计算图解法;杨科之等[8]采用线性衰减荷载等效单自由度法研究了动力系数与延性比的关系,指出了线性衰减荷载计算受限范围;方秦等[9-10]研究了钢筋混凝土梁结构在线性衰减爆炸作用下的弯曲、剪切及弯剪破坏模式,确定了线性衰减荷载作用下梁式构件剪力动力系数理论;Nagata等[11]提出了修正的等效单自由度模型,使等效单自由体系模型能够适用于近场爆炸作用下梁的最大位移计算;师燕超等[12-14]采用可靠度理论分析爆炸荷载,考虑了梁式构件材料、尺寸的不确定性,更新了等效单自由度体系理论及动力系数求解的运用。
从化爆作用荷载参数测试来看,其衰减曲线采用指数型或级数型表达比较合适。线性衰减荷载在等冲量条件下保持超压峰值不变,通过调低正超压作用真实时长,来保证冲击波的正冲量为实际数值,这种简化使冲量、时间比增大,结构设计更保守一些。换言之,对于绝大多数民用建筑结构,可能会导致制造成本偏高。耿少波等[15-16]采用指数型爆炸荷载求解了无阻尼体系下梁式构件动力位移响应及等效静载动力系数,对衰减曲线形状系数对动力系数的影响缺少分析。Gantes等[17]采用软件分析指数型爆炸作用无阻尼单自由度结构的弹塑性位移响应解,指出指数型函数在进行动力学方程求解时较为复杂,可采用其他曲线函数进行解答。
爆炸荷载作为建筑结构承受的一种偶然荷载,不同于其他常规荷载,受炸药的严格管控,目前开展爆炸荷载下的结构试验相对较少,且主要集中在建筑结构典型配筋率、特定截面形式或特殊材料开展[18-19]。因此,加强曲线型衰减爆炸荷载结构响应理论分析成为完善抗爆设计理论的一项重要基础工作。基于弹性的抗爆设计理论简便但会导致制造成本过高,若允许结构进入一定的塑性阶段或形成特定塑性铰,将会降低等效静载动力系数,进而降低抗爆设计工程造价,因此,国内外规范广泛采用考虑延性比的弹塑性进行抗爆设计。结构塑性阶段振动响应与荷载作用时长密切相关,等冲量线性衰减荷载作用时长小于爆炸荷载真实作用时长,这种等效处理方式,必然对等效静载动力系数产生影响;而且不同当量炸药、不同比例距离产生的爆炸荷载衰减曲线波形系数不同,这些参数对动力系数影响如何,国内外鲜有研究。
作者选用能充分反映爆炸荷载曲线衰减形式的级数型数学函数完成动力系数与延性比的计算公式推导,并与现行建筑结构规范、人防工程规范推荐使用的等冲量线性衰减荷载下的动力系数进行对比,进一步考查简化荷载所带来的计算误差。
1 抗爆结构振动微分方程
1.1 爆炸荷载等效单自由度振动方程
根据动力学理论可知,忽略阻尼后的抗爆结构弹性阶段动力学方程为
(1)
式中:Me为等效单自由度体系中等效质量;Ke为等效刚度;Pe(t)为等效荷载;W(t)为观察截面位置结构动位移;t为结构振动的时间变量。
Me=mlkM,Pe(t)=Δp(t)lkL,Ke=KkL
(2)
式中:m为结构单位长度质量;l为结构跨度;kM、kL分别为弹性阶段荷载质量、荷载转换系数;K为结构刚度。进一步定义kML=kM/kL,则式(1)变为
(3)
同理,忽略塑性阶段动力学方程可写为
(4)
式中:kml为塑性阶段等效质量与等效荷载比;qm=KWT/l,WT为弹性阶段最大位移。
从耿少波等的研究可知若采用指数型函数描述曲线爆炸荷载超压函数时为
(5)
式中:Δpm为超压峰值;f(t)为归一化后的超压衰减函数;t+为正超压冲击波作用时长;a为指数型衰减荷载曲线系数。
由图1及函数理论可知,级数型爆炸荷载无法直接确定级数的组成项、组合系数,需先构建幂函数进行幂级数的确定,再进一步确定级数型荷载的函数表达式。其中幂函数描述爆炸荷载超压函数时为

图1 爆炸荷载时长关系图Fig.1 Load duration diagram for different blast loadings
(6)
式中,n为幂函数的次幂。
采用指数型函数作为等冲量基准时,将式(5)在其作用时长内积分后,冲量为
i=Δpmt+[1/a+(e-a-1)/a2]
(7)
同理,可确定等冲量作用下幂函数的次幂为
(8)
分析式(5)可知,曲线波形系数a越大,t+以后的超压函数数值越接近0。结合文献中实测数据,参数a在1~2能充分反映负超压段,本文选用此范围进行分析,此时对应参数n范围为1.72~2.52。n为非自然数时,式(3)及式(4)无解。由此时n最接近的自然数为1与3。若将幂函数型用级数型代替,则有
Δp(t)=Δpmf(t)=
(9)
或
Δp(t)=Δpmf(t)=
(10)
式中,b0、b1为级数型爆炸荷载组合系数。
由杜哈梅积分可知,式(3)对应弹性阶段位移解、速度解为
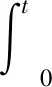
(11)
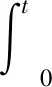
(12)
式中:Wst为Δpm为静载时的静位移;ω为结构振动频率;τ为积分时间参数。
若定义tT为弹性结束时刻,则此时刻位移及对应的速度为

(13)

(14)
由式(3)及式(13)、式(14)可知,塑性阶段结构振动位移及速度为
W(t)=WT+vT(t-tT)+
(15)
(16)
基于理想弹塑性理论的等效静载动力系数为
(17)
1.2 级数型爆炸荷载参数确定
由图1可知,等冲量线性衰减荷载的等效时长为ti,指数型或级数型爆炸荷载的真实作用时长均为t+。以指数型爆炸荷载为基准,根据等冲量线性衰减荷载函数
(18)
将其积分后利用与式(7)的相等条件,可计算出两种荷载作用时长关系
(19)
根据式(9),一三次项级数型荷载冲量为
i=Δpmt+(b0/2+b1/4)
(20)
由式(10),二三次项级数型荷载冲量为
i=Δpmt+(b0/3+b1/4)
(21)
由与指数型冲量相等、超压峰值相等两条件,可分别求出一三次、二三次项级数的组合参数为
b1=2-4/a-4(e-a-1)/a2,b0=1-b1
(22)
b1=4-12/a-12(e-a-1)/a2,b0=1-b1
(23)
2 基于延性比的动力系数理论解
2.1 第一种塑性状态
爆炸荷载真实作用时长t+或等冲量线性衰减荷载等效时长ti数值很小,可认为低于结构弹塑性振动最大位移时间tm。结构完成弹性振动进入塑性的时刻tT存在两种形式:第一种塑性状态,t+(或ti) 令θT=ωtT、θ+=ωt+,对于第一种塑性状态,将式(9)、式(13)代入式(17),可得一三次级数型爆炸荷载动力系数为 (24) 同理可得二三次级数型爆炸荷载动力系数为 (24) 由式(13)、式(14)可得一三次项级数型荷载作用,结构即将进入塑性时弹性振动速度与位移比 (25) 同理,二三次项级数型荷载作用下,结构即将进入塑性时弹性振动速度与位移比 (26) 由式(16)及塑性振动结束时速度为0可知 (27) 由式(15)可知 (28) 由延性比β定义及式(27)、式(28)可知, (29) 从式(29)可以看出,当tT=tm时,即认为结构只有弹性振动无塑性阶段时,结构延性比为1,此时为基于弹性理论的动力系数。 同时由等效单自由度体系参数可知 (30) 式中:Wst为超压峰值视作静载数值时结构静位移;ω为结构振动频率,计算公式为ω2=Ke/Me。 若采用式(25)及式(27)、式(30)代入式(29)后,可得一三次项级数型荷载在第一种塑性状态下,基于动力系数的延性比 (31) 同理,可得二三次项级数型荷载在第一种塑性状态下,基于动力系数的延性比 (32) 因此,根据结构设计所需延性比,结构振动频率、级数型爆炸荷载组合参数、荷载作用时长等参数,即可由式(31)、式(32)进行迭代求出对应的动力系数。 由2.1节第二种塑性状态定义,将式(9)、式(13)代入式(17),可得一三次级数型爆炸荷载动力系数为 (33) 同理可得二三次级数型爆炸荷载动力系数为 (34) 由式(13)、式(14)可得一三次项级数型荷载作用,结构即将进入塑性时弹性振动速度与位移比 (35) 同理,二三次项级数型荷载作用下,结构即将进入塑性时弹性振动速度与位移比 (36) 由式(9)、式(16)及塑性振动结束时速度为0可知,一三次项级数型荷载作用下,进入塑性振动时速度为 (37) 将其代入式(30)后可得 (38) 同理,可得二三次项级数型荷载作用下,进入塑性时振动时速度与位移比 (39) 进一步令θm=ωtm,且令式(36)与式(38)相等时,便可得一三次项级数型荷载作用下表达式 (40) 同理,二三次项级数型荷载作用下表达式为 (41) 由式(15)及延性比定义,经过积分后,对于一三次项级数型荷载作用,其表达式为 (42) 同理,对于二三次项级数型荷载作用,延性比为 (43) 由第二种塑性状态延性比式(42)、式(43)可知,比第一种塑性状态对应的延性比式(31)、式(32)中多一参数θm,此参数不来源于爆炸荷载或结构设计参数,需由式(40)或式(41)求出。 GB 50009—2012《建筑结构荷载规范》指出等冲量线性衰减荷载超压峰值、等效时长来源于GB 50038—2005《人民防空地下室设计规范》;未明确给出动力系数计算公式。因此,以GB 50038—2005《人民防空地下室设计规范》中动力系数计算公式为本文对比基准,完成本文计算工况验证。 弹性及塑性阶段等效质量与等效荷载比kML、kml,由GB 50038—2005《人民防空地下室设计规范》分别取值0.78、0.66;延性比β由GB 50038—2005《人民防空地下室设计规范》中规定的1~4选择典型数据进行;等冲量线性衰减荷载作用下θi由杨科之等、耿少波等的研究中确定的典型数据0.2~2.8进行;爆炸荷载曲线衰减波形系数a由Gantes等研究中的数值表征的典型范围1~2进行。由上述确定的参数数值,进一步形成一三次项、二三次项级数型荷载作用下计算工况,共10种计算工况,如表1所示。 表1 爆炸荷载算例工况Tab.1 Calculation situations for blast loading 完成各种计算工况及对应的规范公式计算后,结果如图2所示。 一三次、二三次项级数型爆炸荷载动力系数曲线均能在两种塑性状态下光滑过渡。在固定的荷载结构参数θi(即ωti)数值下,随着波形系数a的增加,荷载真实作用时长与线性荷载等效时长比值增大,级数型爆炸荷载动力系数也与规范公式计算动力系数差值逐渐增大。所有的计算工况在相同的延性比β作用下,动力系数Kh随θi增大而增大。爆炸荷载及其作用时长ti无法控制降低,有效地降低结构参数ω是一种可行方式。 (a)第一组延性比 等冲量、等峰值、等作用时长条件下,二三次项级数型较一三次项级数型爆炸荷载接近规范公式的动力系数计算结果。当β<2.5且θi<1.2时,可忽略两种级数型荷载动力系数之间差异,与规范线性衰减荷载动力系数最大误差在2%以内,即结构为“密闭、防水要求高”的使用要求时,对于常规武器等化爆作用,可忽略荷载曲线类型,直接采用规范推荐公式;当β<2.5且θi≥1.2时,工况6为所有工况中动力系数最大数值,与规范计算结果差值最小为8.2%,工况5为所有工况中动力系数最小数值,与规范计算结果差值最小为19.8%,此时采用一三次项级数型爆炸荷载是降低造价的一种良好选择;当β≥2.5且θi<1.2时,可忽略级数型爆炸荷载的次项组合情况,选用任何一种级数型爆炸荷载均会降低造价;当β≥2.5且θi≥1.2时,动力系数与级数型爆炸荷载组合次项、波形系数a均发生关联,a=1.0的二三次项级数型爆炸荷载对应的工况6,与规范公式差异最小为10.1%,a=2.0的一三次项级数型爆炸荷载对应的工况1,与规范公式差异最大为37.2%,此时参数θi为1.8。 (1)本文推导完成的化爆作用级数型爆炸荷载模式下动力系数公式,采用真实荷载作用时长的曲线型函数,划分了两种塑性状态,比现行规范线性衰减函数下的爆炸荷载动力系数精准。 (2)级数型爆炸荷载动力系数与曲线波形系数a、项数组合系数b0、b1、结构荷载参数θ+等有关,整体上级数型爆炸荷载动力系数均小于规范计算结果,二三次项级数型较一三次项级数型爆炸荷载动力系数接近规范。 (3)当延性比β<2.5且结构荷载参数θi<1.2时,级数型与线性爆炸荷载模式差异可忽略,可采用人防设计规范提供的简化动力系数公式进行抗爆设计。 (4)当β<2.5且θi≥1.2时,一三次项级数型爆炸荷载动力系数较低,可降低造价;当β≥2.5且θi<1.2时,可忽略级数型爆炸荷载的次项组合情况,选用任何一种级数型爆炸荷载的动力系数均可降低造价;当β≥2.5且θi≥1.2时,若采用较低的动力系数,需考虑级数型次项组合、曲线波形系数a因素后确定。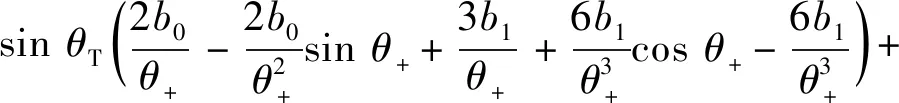
2.2 第二种塑性状态
3 算例验证
3.1 算例工况

3.2 结果分析

4 结 论
