基于多种群遗传与思维进化的混合算法

倪水平，戚海涛，李慧芳

（河南理工大学计算机科学与技术学院，河南焦作 454000）

0 概述

进化算法作为计算机科学与生物进化规律结合发展形成的一类启发式搜索算法，克服了传统优化算法存在的全局寻优能力差、解的质量依赖初始值等缺陷，对求解复杂问题表现出较强的鲁棒性［1］。标准遗传算法（Standard Genetic Algorithm，SGA）［2］作为进化算法的代表之一，广泛应用于图像处理［3］、组合优化［4］、函数优化［5］、车间调度［6］等领域。然而，SGA 存在收敛速度慢、易早熟等问题［7-9］。

为克服SGA 存在的早熟收敛问题，研究者提出自适应遗传算法［10］、免疫遗传算法［11］、小生境遗传算法［12］、基于结构相似度的遗传算法［13］等改进算法，并进行实际应用。但SGA 的这一缺陷与诸多因素有关，并且其控制参数的设定［14］和遗传算子的设计［15］应根据实际问题试探性地进行。文献［16］在SGA 的基础上提出了多种群遗传算法（Multiple Population Genetic Algorithm，MPGA）。MPGA 引入了多种群的概念，通过为不同种群赋予不同控制参数的方式，提高了SGA 控制参数的灵活性，同时，还定义了移民算子和人工选择算子，用于加强各种群之间的联系，实现了多种群协同进化，但该算法的全局寻优能力存在进一步提升的空间［17］。

文献［18］针对早期进化算法存在的问题提出了思维进化算法（Mind Evolution Algorithm，MEA）。MEA 在结构上保留了进化算法的并行性，其定义的趋同操作和异化操作分别用于局部搜索和全局探测，两者相互协调并保持一定的独立性。虽然MEA具有灵活、高效的搜索框架，但其执行过程存在重复搜索、局部寻优能力弱、异化过程生成的临时子群体具有随机性等缺陷。文献［19-20］分别提出了基于禁忌搜索思想和使用小生境技术改进的MEA，解决了MEA 重复搜索的问题。此外，文献［21］使用粒子群算法提高了MEA 的局部寻优能力。

本文提出一种MPGA 与MEA 的混合算法，将MPGA 的寻优机制和遗传操作融入MEA 的搜索框架，以期在保留MPGA 优点的基础上提升MEA 局部搜索精度和全局寻优能力。

1 思维进化算法与多种群遗传算法

1.1 思维进化算法

MEA 是对人类思维进化过程的模拟，其中包含的趋同操作和异化操作使得该算法具有“记忆”和“正向进化”的能力。MEA 中趋同操作、异化操作和成熟子群体的定义分别如下：

定义1子群体范围内的个体为成为胜者而进行竞争的过程称为趋同。

定义2各子群体在解空间范围内为成为胜者而相互竞争并进行不断地探索的过程称为异化。

定义3当一个子群体在趋同过程中不再产生新的胜者时，该子群体称为成熟子群体，其趋同过程也随之结束。

MEA 的寻优流程如图1 所示。

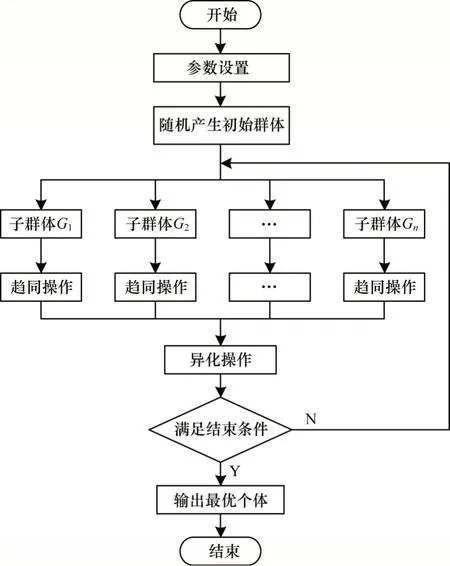
图1 MEA 寻优过程Fig.1 Optimization process of MEA

MEA 在寻优过程中，把全部解空间看作一个群体，再把群体划分为若干个子群体，每个子群体包含对应局部区域的若干个体。适应度得分高的子群体会作为优胜子群体，用于记录全局竞争中优胜者的信息；得分低的子群体则作为临时子群体，用于记录并辅助完成全局竞争的过程。

趋同操作负责各子群体内的局部搜索，该操作的关键步骤是搜寻局部最优个体，并在其临近区域随机生成若干新的成员继续参与搜索，这种寻优方式使得MEA 的搜索精度较低。待子群体成熟后，MEA 执行异化操作，通过查找全局公告板记录的信息释放得分低的子群体，并使在解空间随机生成新的临时子群体继续参与竞争，保证最优解正向进化，这一过程决定着MEA 的全局寻优能力。如此反复迭代，实现全局寻优。

1.2 标准遗传操作

遗传操作是SGA 的核心，包括选择、交叉和变异。3 种遗传操作的实现过程如下：

1）选择操作

从当代群体中以一定的概率选择个体作为父辈，并繁衍下一代。个体被选中的概率与适应度值成正相关，选择操作为后代的质量提供了保障。

GA 常用的选择操作有锦标赛法和轮盘赌法，本文选用基于适应度比例的轮盘赌法。在该选择策略下，选中个体i的概率pi的计算公式如式（1）所示：

其中：N为种群中的个体数目；Fi为个体i的适应度得分。

2）交叉操作

对挑选的2 个个体以一定的概率交换彼此的部分染色体，生成保留父辈特性的新个体。第l个染色体xl和第m个染色体xm在j位的交叉操作如式（2）所示：

其中：b是［0，1］之间的随机数。交叉算子是产生新个体的主要算子，取较大的交叉概率值有助于提升算法的全局寻优能力。

3）变异操作

对种群中的个体以一定的概率改变其一个或多个基因座上的基因值。第i个个体的第j个基因xij执行变异操作如式（3）所示：

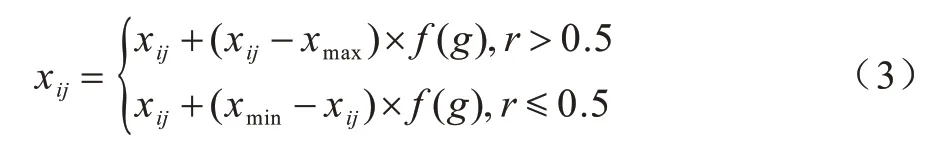
其中：xmax和xmin分别为基因xij的上下界；r为［0，1］区间内的随机数。f(g)的计算公式如式（4）所示：

其中：g为当前迭代次数；r2是一个随机数；Gmax为最大进化次数。变异算子是产生新个体的辅助算子，取较小的变异概率值有利于提高局部寻优的精度。

1.3 多种群遗传算法

与SGA 相比，MPGA 具有以下特点：

1）MPGA 在解空间生成规模、搜索域相同的多个种群中进行并行优化搜索，打破了SGA 单种群进化的框架，其通过对不同种群赋予不同的控制参数，实现不同的搜索目的。

2）各种群之间通过移民算子实现协同进化，最终获得最优解。

3）通过人工选择算子保存各种群在每个进化代中的最优个体，并作为判断算法是否收敛的依据。

MPGA 引入的移民算子和人工选择算子描述如下：

1）移民算子。用源种群中的最优个体定期地替换目标种群中的最差个体。

2）人工选择算子。在进化的每一代选出各种群的最优个体放入精英种群进行保存，并且精英种群不进行选择、交叉、变异等遗传操作。

MPGA 的寻优过程如图2 所示。可以看出，MPGA 中多种群的差异性是由SGA 的不同控制参数来维持的，即交叉概率和变异概率的取值。这2 个参数的计算公式如式（5）所示：

图2 MPGA 寻优过程Fig.2 Optimization process of MPGA

其中：Pcro和Pmut为交叉概率和变异概率的初始值；dcro和dmut为变化的区间长度；rand()为产生随机数的函数；Gn为种群数目。

1.4 算法分析

MEA 定义的趋同操作和异化操作相互独立并彼此协作，任何一方的改进都有利于提高算法的搜索性能：趋同操作并行作用于多个子群体，保证了搜索的高效性；异化操作对成熟子群体进行筛选并探索解空间中新的区域，保证了群体的每一次迭代都是正向进化的。然而，MEA 中各子群体相互独立，不同子群体中的个体无法交流，缺乏寻优多样性，并且趋同操作和异化操作在生成子群体成员时具有随机性，增加了搜索成本同时也降低了寻优的效率和精度。

SGA 的优点是不受约束条件的限制，在进行函数寻优时不依赖于目标函数的梯度信息、连续性及可导性，其所定义的遗传操作可有效降低算法陷入局部最优的可能性，具有突出的全局搜索能力。但同时，SGA 的进化搜索性能受交叉概率、变异概率以及种群规模的影响较大，致使其无法兼顾搜索精度和计算效率，难以找到问题的最优解。MPGA 针对SGA 的缺陷进行了改进，通过多种群协同进化的方式降低单个种群规模对算法的影响，引入移民算子增强种群的多样性，通过对不同种群设置不同的参数降低寻优结果对交叉概率和变异概率取值的敏感度。MPGA 的特性决定了其具有解决大规模、非线性优化问题的能力，但对高维、复杂的多峰函数进行寻优时，仍存在不可忽略的早熟收敛风险。

通过以上分析可知：MEA 具有灵活、高效的寻优框架，趋同操作和异化操作均可单独进行改进；MPGA 具有多种群协同寻优的特点，能够对种群所在的连续区域进行全面、细致的搜索，但各初始种群的分布会影响其搜寻最优解的能力。由于这2 种算法的操作都是面向多种群/子群体的，因此存在一定的相似性，这为本文将MPGA 嵌入MEA 提供了理论基础。MPGA 的寻优机制可辅助MEA 趋同操作的执行，增强子群体间的交互，实现局部精细化寻优，保证成熟子群体的质量，并且选择、交叉和变异算子用于异化过程可以提升临时子群体的质量，避免低效搜索。同时，异化操作又能指导新一轮的迭代继续向有利方向进行，最终实现提高MEA 局部寻优精度和全局收敛能力的目的。

2 MPGA 与MEA 的混合算法

2.1 混合策略

本文将MPGA 和MEA 相结合，提出MPGA-MEA算法，混合策略为：利用MPGA 的寻优过程替代MEA子群体内的个体竞争，并在局部公告板中定期记录子群体的最优个体用于移民操作，当局部公告板不再更新时，判定其对应的子群体成熟，此时更新全局公告板，释放得分低的成熟子群体。在此基础上，利用全局公告板信息选择父代，对选中的个体执行交叉、变异操作，将产生的子代个体作为中心个体，以此生成高质量的临时子群体，用于下一轮的迭代寻优。

MPGA-MEA 寻优的简化过程如图3 所示，具体步骤如下：

图3 MPGA-MEA 寻优过程Fig.3 Optimization process of MPGA-MEA

步骤1参数设置。设群体规模为PPopsize，优胜子群体的数量为SN，临时子群体的数量为TN，子群体规模NNind=PPopsize/(SN+TN)。

步骤2群体初始化。在解空间内随机生成规模为PPopsize的群体，并根据适应度得分进行排序。取得分最高的(SN+TN)个个体作为中心个体，在以它们为中心的一定区域内分别产生规模为NNind的SN个优胜子群体和TN个临时子群体。

步骤4异化操作。完成临时子群体和优胜子群体的替换和释放，并选择全局公告板中记录的优胜个体执行交叉、变异操作得到新个体，在以该个体为中心的一定区域内生成新的临时子群体参与下一轮竞争，保证子群体的总数不变。

步骤5判断是否满足终止条件。若是，结束迭代并输出结果；否则，返回步骤3，进行下一轮迭代搜索。

2.2 算法实现

MPGA-MEA 算法实现伪代码如下：

算法1MPGA-MEA

上述伪代码中各部分与算法步骤的对应关系如下：输入参数设置对应于步骤1；1～3对应于步骤2；5和6对应于步骤3；7.1～7.5 对应于步骤4；4 和8～10 对应于步骤5。通过算法描述可知，MPGA-MEA的迭代包括2种：1）步骤3 中MPGA 的寻优过程，子群体需要进行多次迭代直至成熟，记为内部迭代；2）步骤5 MEA 框架中的迭代，用于辅助子群体正向进化，记为外部迭代。

3 测试与分析

3.1 测试函数与对比算法

为验证MPGA-MEA 的性能，选取表1 中列出的6 个标准测试函数进行寻优测试，其中：f1、f2、f3分别为碗状、板状、山谷状的单峰函数，常用于检测算法的收敛性能和搜索精度；f4、f5、f6为局部极值点分布规律各异的多峰函数，可有效检测算法对复杂优化问题的全局搜索能力。6 个标准测试函数的搜索域各不相同，全局最小值均为0。

表1 测试函数Table 1 Test functions

选择MPGA 和MEA 作为MPGA-MEA 的对比算法。各算法的时间复杂度与具体的参数设置有关，为降低计算成本，需要根据目标函数的寻优难度和变量维度分别设置合理的初始参数。

3.2 测试结果及分析

本文对不同维度的测试函数设置不同的目标精度，如表2 所示。当算法搜索到满足目标精度的最优解时停止运行，同时为算法陷入局部极值的情况设置相应的终止条件。每个算法对不同维度的测试函数运行50 次，适应度函数即为对应的测试函数。

表2 测试函数在不同维度下的目标精度Table 2 Target accuracy of the test functions under different dimensions

选用寻优成功率、最差解和耗时作为算法的评价指标。寻优成功率表示算法寻优值达到目标精度的测试次数占测试总次数的百分比；最差解是在算法寻优失败的测试中所搜索到的最差目标值精度；耗时即每次搜索的总用时，评价时取50 次测试用时的平均值用于对比。测试环境为64 位Windows10操作系统，Intel®CoreTMi7-4510U 处理器，仿真平台为MATLAB R2017b，MPGA 的相关操作借助Sheffield 遗传算法工具箱完成。

俗话说：“书中自有黄金屋，书中自有颜如玉。”最令我开心的既不是去旅游，也不是品尝美食，而是在图书馆中遨游。

3.2.1 单峰函数测试与分析

设置MPGA 和MPGA-MEA 的交叉概率Pcro=0.4，变异概率Pmut=0.2，最优个体的保持代数MMaxGen=3；MEA子群体最优个体的保持代数为10；MPGA-MEA 的最大外部迭代次数IIter=10；算法的各种群/子群体中的个体数NNind=30。在对不同维度的单峰函数寻优时，其他主要参数设置如表3 所示。其中，MP为种群数，SN、TN分别为优胜子群体和临时子群体的数量。

表3 3 种算法在不同维度下的关键参数设置Table 3 Key parameters settings of three algorithms under different dimensions

表4 列出了各算法对单峰函数的测试结果。可以看出：对于碗状函数Sphere，MPGA 和MPGA-MEA 都具有良好的寻优效果，MPGA-MEA 平均耗时略小于MPGA，MEA 的搜索结果与目标精度相差很大；对于板状函数Zakharov，最优值附近梯度变化平缓，寻优难度高，MEA 仅在维度取2 时有30%的寻优成功率，在高维度下寻优能力弱，MPGA 和MPGA-MEA 的寻优能力接近，但MPGA-MEA 的平均耗时更短；对于2 维的山谷状函数Rosenbrock，仅有MPGA-MEA 的寻优成功率为100%，且耗时最短，当维度取值为50、100、200时MEA难以达到目标精度，但寻优结果与目标精度接近，而MPGA 在高维度下用时较短。

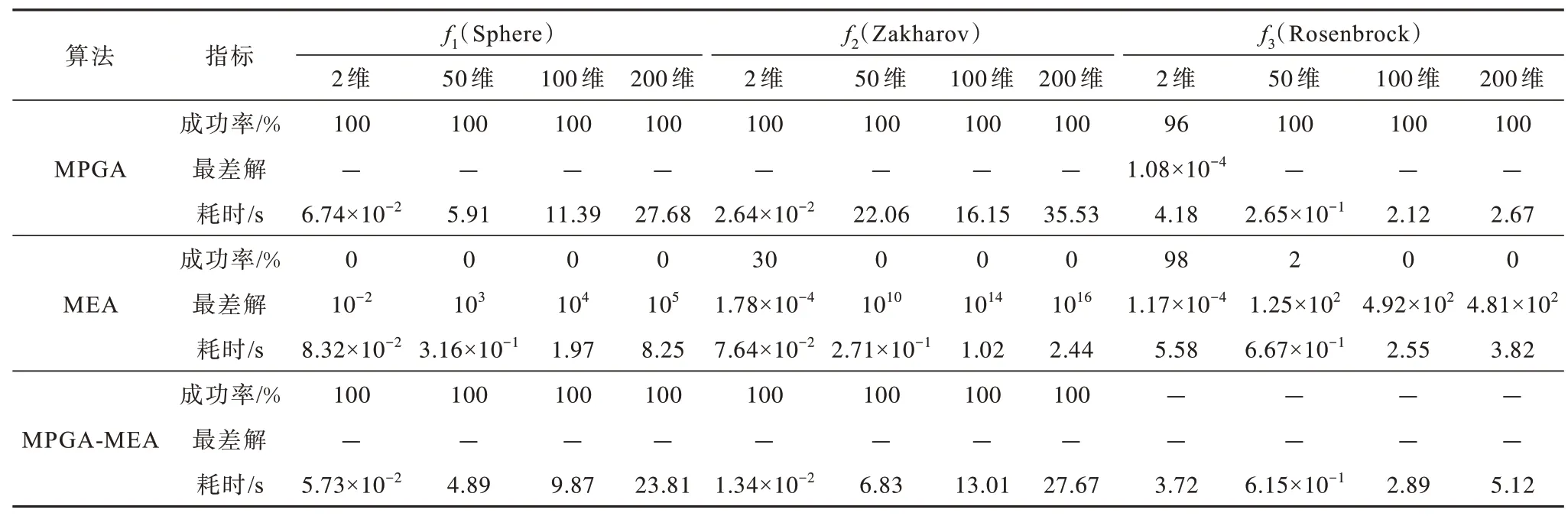
表4 3 种算法对单峰函数的寻优性能比较Table 4 Comparison of optimization performance of three algorithms for unimodal functions

通过以上分析可知，MPGA-MEA 对单峰函数的寻优成功率最高，MPGA次之，MEA的搜索精度远低于前两者。MPGA 和MPGA-MEA 对单峰函数的综合寻优能力比较接近，对于MPGA存在寻优失败的情况（如2维的f3函数），MPGA-MEA可以通过异化操作对最优值所在的局部区域加强搜索，直至满足结束条件。为对MPGA和MPGA-MEA 的收敛规律做进一步比较，绘制f1～f3在2维和100维时的收敛曲线，如图4所示。

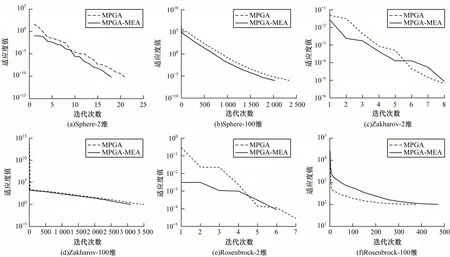
图4 MPGA 和MPGA-MEA 算法对单峰函数寻优的收敛曲线对比Fig.4 Comparison of convergence curves of MPGA and MPGA-MEA algorithms for unimodal functions optimization

由于MPGA-MEA 的迭代为优胜子群体或临时子群体执行的内部迭代，因此MPGA-MEA 参与执行1 次迭代的子群体数少于MPGA 参与1 次迭代的种群数。同时由于单峰函数不存在局部极值，因此一般无需执行MPGA-MEA 的异化操作，图4 实质是比较MPGA-MEA 中趋同操作和MPGA 的收敛能力。

MPGA-MEA 的子群体是以全局优质个体为中心生成的多个小范围种群，因而其收敛曲线的起点一般优于随机分布的MPGA 的起点。此外，MPGA 的收敛过程变化相对平稳，MPGA-MEA 对寻优难度低的函数迭代次数更少，但两者收敛曲线的整体变化趋势相似。

3.2.2 多峰函数测试与分析

设置MPGA 和MPGA-MEA 的交叉概率Pcro=0.4，变异概率Pmut=0.2，最优个体保持代数MMaxGen=3；MEA子群体最优个体保持代数为10；MPGA-MEA 和MEA的最大迭代次数IIter=30；算法的各种群/子群体中的个体数NNind=30。由于不同的多峰函数寻优难度相差较大，为保证算法的寻优能力和对比的公平性，对多峰函数的不同维度进行寻优时，分别设置不同的种群和子群体数量，如表5～表7所示。其中：MP为种群数；SN、TN分别为优胜子群体和临时子群体的数量。

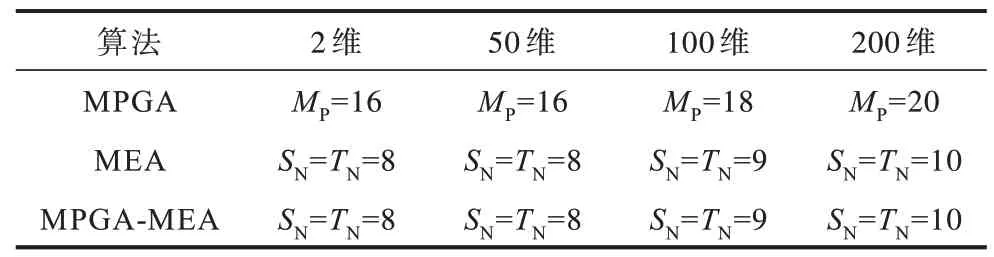
表5 3 种算法对f4的参数设置Table 5 Parameters settings of three algorithms to f4

表6 3 种算法对f5的参数设置Table 6 Parameters settings of thress algorithms to f5

表7 3 种算法对f6的参数设置Table 7 Parameters setting of three algorithms to f6

表8 列出了各算法对多峰函数的测试结果。可以看出：格栅函数Griewank 具有很多规律分布的局部极小值，MPGA 有较大几率陷入局部极值致使寻优失败，此时搜索到的最优值坐标与实际最优值坐标发生明显偏离，MPGA-MEA 的趋同操作同样存在陷入局部极值的风险，得益于异化操作的介入，其能够以较低的代价在最优值附近重新生成新的临时子群体参与迭代搜索，直至满足结束条件，MEA 的寻优成功率为0，且与目标精度相差甚远；Rastrigin 函数的寻优难度会随着维度的增加迅速增大，使得各算法均无法搜索到高精度的目标值，因此，在高维度下设置的目标精度较低，该目标精度下MPGA 的寻优失败率低，MPGA 和MPGA-MEA 的平均耗时无明显差距，但后者的寻优成功率稳定在100%，MEA 无法达到目标精度；Ackley 函数广泛用于测试优化算法，该函数最优值附近的梯度变化大，寻优难度相对较低，MPGA 和MPGA-MEA 在不同维度下都能以较高的精度收敛到最优值附近，两者耗时相近，MPGA-MEA 的寻优成功率较高，MEA 的搜索精度远低于目标精度。

表8 3 种算法对多峰函数的寻优性能比较Table 8 Comparison of optimization performance of three algorithms for multimodal functions

通过以上对比可知，MPGA-MEA 对多峰函数的寻优能力突出，即使在高纬度下，该算法依旧具备很强的跳出局部极值的能力，可以较低的计算成本提高寻优成功率；MPGA 在解决高维度、多极点问题时存在不同程度陷入局部极值的风险，寻优失败的搜索过程耗时也略高；MEA的寻优精度远低于前两者。为对比MPGA和MPGA-MEA 的收敛特性，绘制f4～f6在2 维和100 维时MPGA 和MPGA-MEA 的收敛曲线，如图5 所示。

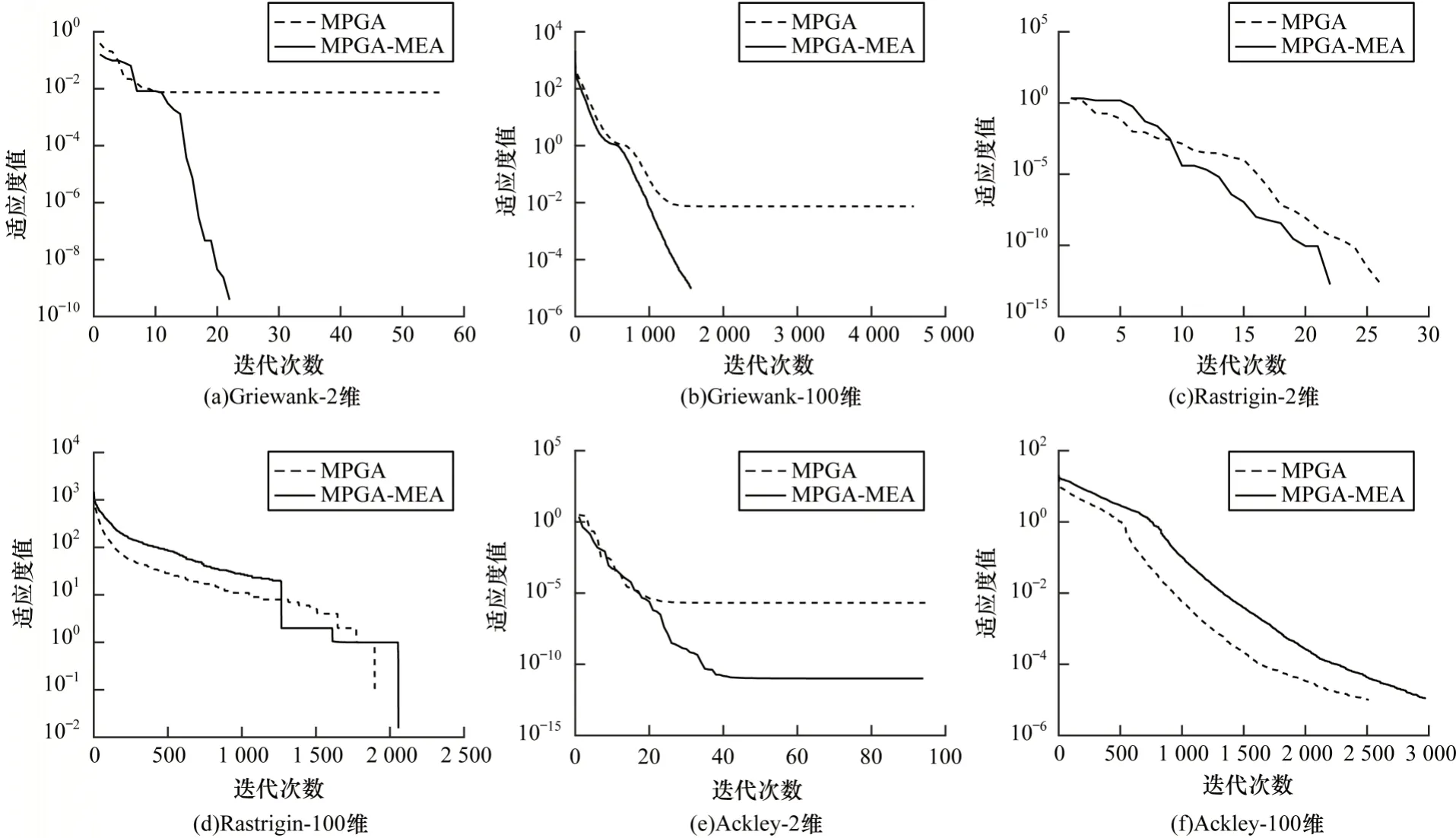
图5 MPGA 和MPGA-MEA 算法对多峰函数的寻优曲线对比Fig.5 Comparison of optimization curves of MPGA and MPGA-MEA algorithms for multimodal functions

选取MPGA 对函数Griewank 寻优失败的收敛曲线进行对比，如图5（a）和图5（b）所示，可以看出：MPGAMEA 的收敛精度明显优于MPGA，但两者在前期的收敛曲线变化一致；当维度取2 时，MPGA 在第10 次迭代时便陷入局部极值，直至寻优结束也未能跳出；当维度为100时，MPGA约在第1 300次迭代时陷入局部极值，直至结束寻优过程；MPGA-MEA能利用异化操作跳出局部极值，生成新的子群体参与下轮搜索。

选取MPGA 对函数Rastrigin 寻优成功的收敛曲线进行对比，如图5（c）和图5（d）所示，可以看出，MPGA 和MPGA-MEA 的收敛规律相似。

选取MPGA 对函数Ackley 寻优失败和成功的收敛曲线进行对比，如图5（e）和图5（f）所示，可以看出：维度为2 时，MPGA 前20 次迭代过程的收敛曲线变化和MPGA-MEA 相似，然后MPGA 陷入局部极值；当维度为100 时，两者的收敛曲线变化规律相似。

综上可知：MPGA-MEA 对单峰函数的寻优能力与MPGA 相近，远高于MEA；对高维、复杂的多峰函数进行寻优时，MPGA-MEA 的优势明显，可在保证运算效率的同时，有效克服MPGA 和MEA 早熟收敛的缺陷。

4 结束语

本文分析MPGA 和MEA 的优缺点，从优势互补的角度出发设计混合算法MPGA-MEA。该算法以MEA 为框架，以MPGA 为内核，将MPGA 的寻优机制和遗传操作应用到MEA 的趋同操作和异化过程中，优化趋同操作对各子群体的搜索效果，提高异化过程中生成的临时子群体的质量，实现对MEA 局部搜索精度和全局寻优能力的均衡提升。仿真实验结果验证了MPGA-MEA 优越的综合性能。由于条件受限，本文仅对MPGA-MEA 进行理论分析和部分标准测试函数的仿真验证，下一步将研究高维度下提升MPGA-MEA 寻优效率和搜索精度更优的参数设置，探索各参数取值和算法性能之间的关系，并将现有对MPGA 的改进方法应用到MPGA-MEA 的趋同操作中，以进一步提升算法的搜索性能。