永磁涡流耦合器传递转矩计算方法研究

程习康, 刘 巍, 孙明浩, 罗唯奇

(大连理工大学 机械工程学院, 辽宁 大连 116024)

随着全球经济的高速发展,目前人类面临着日益严重的环境破坏、资源匮乏、生态污染等问题,发展以节能、高效、环保为理念的清洁绿色产品对人类可持续发展具有重要意义,永磁涡流耦合器在这种产品理念驱动下产生[1].永磁涡流耦合器作为一种新型的非接触传动装置,具有结构简单、节能高效、传动平稳、无污染、允许主从动轴不对中等特点,而且具有良好的环境适应性[2-4].与液力耦合器和变频器相比,液力耦合器可控性差且存在喷油污染,低速时无法平滑加速;变频器故障率高、环境适应性差,产生谐波污染进而影响电网,而永磁涡流耦合器在实现转矩调节和传递的同时,可有效地规避上述问题,因此一定程度上可以替代液力耦合器和变频器,在汽轮机、冷却泵、皮带运输机、大型刮板机、破碎机、球磨机等重大工程装备中具有较好应用前景[5-7].

永磁涡流耦合器最早由美国MagnaDrive公司应用在尼米兹号和斯坦尼斯号航空母舰的海水泵上,后来扩展到民用行业,并于2008年引进到中国.近年来,国内外学者针对永磁涡流耦合器的传递转矩进行了大量的研究.Canova等[8]基于分离变量法将永磁涡流耦合器从三维问题简化为二维,得到了转矩-转速关系的纯解析模型;文献[9-11]考虑了材料的磁饱和及永磁体本身特性,同时考虑了三维结构参数,建立了一种可处理复杂结构的永磁涡流耦合器传递转矩预测模型,并将该模型与有限元结果对比,得到了一致性较好的评价;文献[12-14]在平均半径处进行线性化假设,求解了三维麦克斯韦方程,研究了磁极对数、气隙长度等几何参数的影响,建立了一种新的永磁涡流耦合器传动性能二维解析模型,并将计算的转矩与有限元和实验结果进行了比较;Erasmus等[15]提出了一种求解径向磁通永磁涡流耦合器转矩的半解析计算方法,考虑了磁通密度谐波的影响,采用罗素系数顾及了三维端部效应,通过实验验证了半解析转矩计算方法的正确性.

国内针对永磁涡流耦合器的研究起步较晚.杨超君等[16]以层理论为指导,分析并得到了永磁涡流耦合器的转矩计算方法,然后通过有限元方法分析三维瞬态磁场的分布,并得到了关键参数如气隙长度、永磁体厚度、磁极数、从动盘的槽数、槽深以及主动转速等对转矩计算结果的影响;文献[17-18]基于等效磁路法建立了永磁涡流耦合器的解析模型,分析了永磁涡流耦合器各区域磁导和漏磁,求解出气隙中的磁感应强度,进而推导出转矩计算公式;何富君等[19]利用Ansoft Maxwell仿真软件建立了永磁涡流耦合器三维有限元模型,对耦合器的传动特性进行仿真研究,得到传递转矩与间隙、转速差之间的对应关系;李德永等[20]以电磁感应原理为基础,提出了简化的永磁体阵列三维模型,基于洛伦兹定律建立了转矩的解析模型,并和有限元结果进行了对比,分析了永磁涡流耦合器动态特性的影响因素.

与上述研究不同,本文以一台6磁极对数、额定输入转速1 450 r/min的永磁涡流耦合器为例,首先以永磁涡流耦合器的三维复杂结构为导向,提出了一种更加简单且有效的等效磁路模型,然后基于安培环路定律,对样机的传递转矩进行解析计算,最后建立三维有限元模型和实验平台对转矩进行了验证,与实验结果对比,计算方法具有较好的精度.

1 永磁涡流耦合器几何结构及磁路

1.1 永磁涡流耦合器几何结构

永磁涡流耦合器主要由两部分组成:其中一部分是导体转子,包含导体轭铁和导体盘;另一部分是磁体转子,包含磁体盘、永磁体和磁体轭铁.电机端连接导体转子并进行旋转,导体转子切割磁体转子的N/S交替磁场,根据法拉第电磁感应定律,导体转子内将产生变化的涡流磁场,在永磁体本身磁场和涡流磁场的交互下,实现了电机端到负载端的转矩传递.永磁涡流耦合器几何结构如图1所示,导体转子和磁体转子之间存在着气隙,通过改变气隙厚度可以实现转矩大小的调节.此外,导体轭铁和磁体轭铁的作用是保证磁力线的收敛.

图1 永磁涡流耦合器几何结构

图1中,li1为导体轭铁厚度,lcs为导体盘厚度,la为气隙厚度,lp为磁体盘厚度,lpm为永磁体厚度,li2为磁体轭铁厚度,r2为导体盘外径,r1为导体盘内径,rp2为永磁体外径,rp1为永磁体内径,rav为永磁体平均半径,wpm为永磁体径向宽度,τm为相邻永磁体之间的距离,τp为相邻永磁体中心之间的距离.

1.2 永磁涡流耦合器磁路

永磁涡流耦合器磁路可以有效地表示其磁力线走向,这是分析并计算传递转矩的重要前提.为了得到这一磁路,采用有限元方法对永磁涡流耦合器进行了分析.如图2所示,由于永磁涡流耦合器属于对称结构,这里只建立了包含一对永磁体的永磁涡流耦合器磁路.①表示永磁涡流耦合器的主磁路,其磁力线走线为:永磁体→磁体盘→导体盘→导体轭铁→导体盘→磁体盘→永磁体→磁体轭铁→永磁体;②表示永磁涡流耦合器的第一泄漏磁路,其磁力线走向为:永磁体→磁体盘→导体盘→磁体盘→永磁体→磁体轭铁→永磁体;③表示永磁涡流耦合器的第二泄漏磁路,其磁力线走向为:永磁体→磁体盘→磁体轭铁→永磁体.

图2 永磁涡流耦合器磁路

2 有效磁通量求解

2.1 泄漏磁阻求解

根据图2的第一泄漏磁路②和第二泄漏磁路③,可以分别计算出第一泄漏磁阻和第二泄漏磁阻.第一泄漏磁阻主要存在于气隙和导体盘处,存在如下关系:

(1)

式中:Rl1为第一泄漏磁阻;μ0为真空磁导率;μa空气磁导率;xa为第一漏磁积分边界条件.

第二泄漏磁阻主要存在于永磁体本身之间,存在如下关系:

(2)

式中:Rl2为第二泄漏磁阻;xb为第二漏磁积分边界条件.

根据第一泄漏磁阻和第二泄漏磁阻,获得总泄漏磁阻和总泄漏磁导的表达式为

(3)

式中:Rl为总泄漏磁阻;Λl为总泄漏磁导.

2.2 有效磁动势求解

在永磁涡流耦合器结构中,永磁体是可靠的磁源,负责提供稳定有效的磁场.根据永磁体本身的属性,可以得到原有磁动势为

F0=Hpmlpm.

(4)

式中,Hpm为永磁体矫顽力.

类似于电路中电源的内阻,永磁体本身也存在磁阻,这个永磁体磁阻的表达式为

(5)

式中：Rpm为永磁体磁阻;μpm为永磁体相对磁感应强度.

根据磁导与磁阻的关系,进一步获得永磁体磁导为

Λpm=1/Rpm.

(6)

本质上来说,由式(3)获得的总泄漏磁导相对于永磁体磁导是一种磁损耗.因此,根据式(1)～(6)可以获得有效磁动势为

(7)

式中,kr为有效磁阻修正系数,其数值按经验获取,不同的应用场合数值略有不同.

2.3 有效磁通量求解

永磁涡流耦合器各部分都存在磁阻,导体盘磁阻的表达式为

(8)

式中，μcs为导体盘相对磁导率.

气隙磁阻的表达式为

(9)

磁体盘磁阻为

(10)

式中,μp为磁体盘相对磁感应强度.

导体轭铁磁阻和磁体轭铁磁阻为

(11)

式中:Ri1为导体轭铁磁阻;Ri2为磁体轭铁磁阻;μi1为导体轭铁相对磁导率;μi2为磁体轭铁相对磁导率.

在图2中,虽然建立了永磁涡流耦合器磁路,但是该磁路涉及的磁力线路径相对复杂,不能直接反映出有效磁通.根据上文的分析,图3建立了一个简单且有效的永磁涡流耦合器等效磁路模型.

根据图3建立的等效磁路模型和式(7)获得的有效磁动势,求得有效磁通量为

(12)

图3 永磁涡流耦合器等效磁路模型

3 传递转矩模型

3.1 有效涡流深度

永磁涡流耦合器正常运转时,导体盘和磁体盘之间存在转速差,促使穿过导体盘的磁通量方向和大小随时间呈现周期性变化.根据法拉第电磁感应定律,导致导体盘上产生围绕磁通量变化方向的涡流.该涡流并不是完全存在于导体盘内,而是集中于导体盘表层,越接近于导体盘表面,涡电流密度越大,这一现象被称为趋肤效应.初始趋肤深度为

(13)

式中:p为磁极对数;Δn为导体盘和磁体盘之间的转速差;σcs为导体盘电导率.

考虑到涡电流密度在导体盘深度方向(z方向)呈现指数级递减,涡电流密度和趋肤深度满足方程

(14)

式中:J为涡电流密度;ld为有效趋肤深度.

对式(14)进行求解,得到有效趋肤深度为

ld=(1-1/e)ld0.

(15)

进一步化简,得到有效涡流深度为

lce=min(lcs,ld) .

(16)

3.2 磁感应强度求解

为了更清晰理解建模过程,在永磁体剖切视图和导体盘视图下,图4建立了涡流区域的坐标系位置.该坐标系以永磁体正对导体盘的中心为原点,垂直于导体盘为z方向.

图4 涡流区域坐标系位置示意图

当导体盘切割磁力线运动时,不仅应该考虑永磁体本身磁场,同时应该考虑涡流产生的感应磁场.因此,建模时必须将磁感应强度划分为有效磁感应强度和感生磁感应强度,得到[10]

B(y)=Be(y)+Bi(y) .

(17)

式中:B(y)为磁感应强度;Be(y)为有效磁感应强度;Bi(y)为感生磁感应强度.其中,根据式(12)的结果和图4建立的坐标系,得到有效磁感应强度为

(18)

涡电流密度和磁感应强度的关系为[10-11]

J(y)=σcsΔωravB(y) .

(19)

式中:Δω为导体盘和磁体盘之间的角速度差,Δω=2πΔn/60.

根据安培环路定理,得到

(20)

进一步对式(20)化简得到

(21)

对式(21)进一步化简得到

k=μ0σcsΔωravlce/[2(lp-lpm+la+lce)].

(22)

式中,k为中间变量代号,使用k是为了让表达式简洁.

对式(22)进行微分,得到

dBi(y)=kBe(y)+kBi(y),y∈[-τp/2,τp/2] .

(23)

对式(23)进行求解,得到

(24)

式(24)中,必定存在一个y0使得Bi2(y=y0)=0成立,得到

c2=Bee-ky0.

(25)

由于涡流区域对称分布,在区间[-τp/2,y0]和区间[y0,τp/2]的涡流大小是一样的,得到

(26)

根据函数的连续性,得到

(27)

结合式(25)～(27),y0,c1,c2,c3可以计算得到:

(28)

将式(28)代入到式(24)中,得到

(29)

求得感生磁感应强度后,磁感应强度可以由式(17)计算获得.

3.3 传递转矩求解

根据式(19)得到的J(y),得到单个涡流区域的传递功率为

(30)

进一步对式(30)积分得到

(31)

考虑到磁极对数的影响,得到初始传递转矩：

(32)

如图5所示,涡流区域被划分为悬垂区和中心区,只有存在于中心区的涡电流对转矩传递产生实质作用,这种现象被称为三维端部效应.考虑到这种端部效应[3],必须对初始传递转矩进行修正.该修正系数为

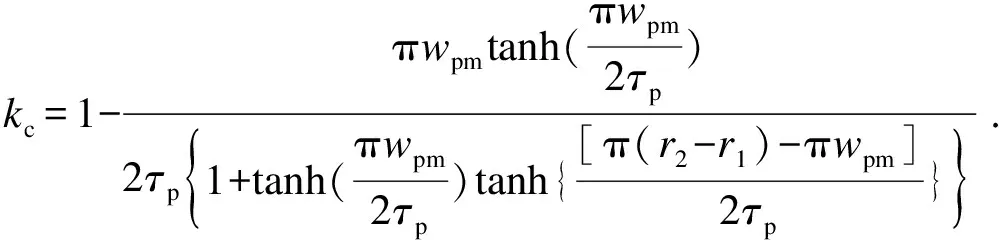
(33)

图5 三维端部效应

对初始传递转矩修正后,得到传递转矩为

T=kcT0.

(34)

4 试验验证

4.1 试验平台

为了验证本文提出的永磁涡流耦合器传递转矩计算方法,同时为了弥补实验和有限元方法本身的误差,建立了如图6所示的传递转矩试验平台和如图7所示的三维有限元分析模型.其中,三相异步电机是试验平台的动力源,其额定输入转速为1 450 r/min.转矩转速传感器分别设置在电机端和负载端,可有效测量永磁涡流耦合器的转速差和转矩.气隙调节器可以改变永磁涡流耦合器导体盘和磁体盘之间的气隙大小,其调节范围为4～30 mm.

图6 永磁涡流耦合器试验平台

图7 三维有限元分析模型

同时,设置了所制作的永磁涡流耦合器样机的详细参数(表1).

表1 永磁涡流耦合器样机参数

4.2 试验结果和对比分析

试验时,三相异步电机输出转速设定为1 450 r/min,同时调整负载大小可以实现对转速差的改变,转矩转速传感器将转矩数据上传到上位机.试验数据的获取必须待永磁涡流耦合器运行稳定之后,以气隙厚度4 mm和转速差5 r/min为例,在30 min内传递转矩波动小于2%,此时获得的数据可作为最终传递转矩结果,如图8所示.

图8 30 min内的传递转矩波动

永磁涡流耦合器正常运转下,气隙厚度一般在10 mm以内,设定气隙厚度分别为4 mm和6 mm,将采用本文方法计算的结果与试验结果和有限元结果进行对比,如图9所示.

从图9的对比结果可以看出,在转速差小于100 r/min的情况下,所提传递转矩计算方法与试验和有限元结果有较好的一致性,其相对误差在6%以内.所提方法的计算结果略大于试验和有限元结果,这是因为在建模过程中未充分考虑到机械损耗和发热损耗的影响.在转速差大于100 r/min时,所提方法与试验和有限元结果之间的误差逐渐增大,在转速差达到200 r/min时,相对误差接近10%,这是因为随着转速差增大,所提方法无法准确衡量漏磁的大小,同时也无法顾及在大转速差条件下,发热对磁场的影响.另外,随着转速差的增大,传递转矩不断增大,但是在转速差大于150 r/min时,所提方法获得的传递转矩增速放缓且有减小的趋势,而试验与有限元结果没有减小的趋势,这是因为三相异步电机具有承受120%～150%过载的能力.实际运行过程中,永磁涡流耦合器的转速差在100 r/min以内,因此该永磁涡流耦合器传递转矩计算方法,满足实际要求,具有较好的工程应用价值.

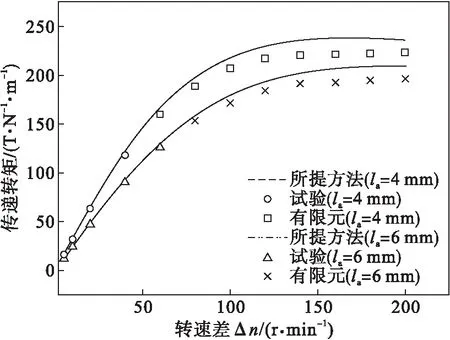
图9 永磁涡流耦合器传递转矩和转速差关系

设定转速差为50 r/min,图10进一步建立了传递转矩在不同气隙厚度条件下的变化关系,可以看出,所提方法和试验结果具有较好的一致性,相对误差在6%以内.同时,随着气隙厚度的增加,传递转矩不断降低,这是因为气隙厚度的增大导致磁场的减弱.

图10 永磁涡流耦合器传递转矩和气隙厚度关系

4.3 预测和建议

永磁涡流耦合器样机制作完成之后,如果通过改变零件几何尺寸,重新开展试验和设计优化,成本较高.所提方法完全依赖于永磁涡流耦合器的几何参数,采用所提方法进行设计优化可以有效节约成本和时间.设定气隙厚度为4 mm和转速差为50 r/min,图11建立了永磁涡流耦合器传递转矩和导体盘厚度关系,图12建立了永磁涡流耦合器传递转矩和磁极对数关系.从图11可以看出,随着导体盘厚度的增加,传递转矩不断减小,在满足负载所需转矩要求的情况下,可以采用较小的导体盘厚度,这样可以减少导体盘的质量,腾出更大的设计空间.从图12可以看出,随着磁极对数的增加,传递转矩增加明显,若负载所需转矩

图11 永磁涡流耦合器传递转矩和导体盘厚度关系

图12 永磁涡流耦合器传递转矩和磁极对数关系

无法满足要求,可以考虑增加磁极对数来增大传递转矩,但增加磁极对数的同时也要增加磁体盘直径,否则无法装载足够多的永磁体.因此,在实际工程中,所提出的传递转矩计算方法对永磁涡流耦合器的设计优化具有参考价值.

5 结 论

1) 本文以二维有限元仿真结果为指导,建立了永磁涡流耦合器的等效磁路模型,获得了传递转矩的解析结果.与试验和有限元结果对比,在正常的转速差范围内(<100 r/min),所提传递转矩计算方法具有较好的一致性,相对误差在6%以内.但是在较大的气隙和转差下,由于漏磁和热损耗无法准确虑及，计算结果有所失准.

2) 本文提出的永磁涡流耦合器传递转矩计算方法,完全依赖于零部件的几何参数,可以节约时间成本和费用成本.研究结果对永磁涡流耦合器的设计和优化具有指导意义和参考价值.