四川地区M5.0及以上地震时间间隔统计分析与概率预测

王 璇

（上海对外经贸大学统计与信息学院，上海201620）

地震发生时间间隔的分布特征一直以来都是地震学家感兴趣的话题，了解区域地震发生时间间隔对地震区划、地震预报、地震危险性分析和地震灾害预测具有重要意义。中国位于环太平洋地震带和欧亚地震带的交汇部位，是一个震灾严重的国家，地震活动频度高、强度大、震源浅、分布广。基于地质的地震研究的作用不可否认，通过运用沉积地质学、地貌学和构造地质学等常用方法有助于评估未来地震发生概率（刘静等，2021），这些方法的局限性在于许多地震不会在确定的断层出现，因此，将统计学应用到地震发生和预测上很有意义。本文将地震发生看作一个统计过程，假设地震发生时间间隔是与一些概率分布模型相关联的随机变量，找出地震发生时间间隔的最佳拟合概率分布函数，它的分布特征对研究地震活动的复发和预测未来的地震有重要作用。

自从概率统计方法与地震预报研究相结合以来，许多学者对地震发生时间间隔的统计规律进行了不同程度的研究。于利民等（1996）对中国大陆有史以来的强地震发生时间间隔进行分析，得出强震时间间隔的经验概率和模拟函数。范琦（2001）以甘肃天祝地区为例，利用最大熵原理进行分析检验，结果认为地震震级和地震间隔时间的变化服从威布尔分布。李强和徐桂明（2002）利用威布尔分布建立了江苏及邻区中强地震的时间间隔分布模型，并对该地区未来几年发生中强地震的概率进行预测。王炜和刘震华（1987）探讨了华北地区小震时间间隔的统计分布，经过统计检验认为它服从威布尔分布。张亚奎（1996）对吉林省伊通—舒兰断裂带以及我国南北地震带南段安宁河—滇东地震带发生的地震进行了统计分析，发现在大的地震带上发震时间间隔服从正态分布。Utsu（1984）使用威布尔分布、伽马分布、对数正态分布和指数分布估计日本地区的地震发生时间间隔。Sadeghian（2018）研究适用于伊朗地区的地震时间间隔数据的概率密度函数，结果为伽马分布、贝塔分布、指数分布、对数正态分布、正态分布和威布尔分布。Khan等（2021）根据拟合优度检验，得出威布尔分布和对数逻辑分布是兴都库什地区最佳拟合模型，对数正态分布和伽马分布分别为该地区第二和第三合适的概率模型。Somette和Knopoff（1997）基于威布尔分布、对数正态分布、指数分布、伽马分布和贝塔分布等5种概率分布研究了地震时间间隔并预测地震复发时间。

2008年5月12日，四川汶川发生8.0级大地震，破坏性极强、波及范围广，造成了非常严重的人员伤亡和经济损失。在四川发生过的中小地震更是数不胜数，因此本文选取中国四川地区发生的中强地震作为研究对象，从指数分布、伽马分布、对数正态分布和威布尔分布4种概率分布出发，分别研究1970年至2007年和1970年至今发生的M5.0及以上地震，通过拟合优度检验找出地震发生时间间隔的最佳拟合分布，并评估未来发生M5.0及以上地震的概率。

1 数据与方法

1.1 地震数据

根据国家地震科学数据中心记载（1970年1月1日至2021年7月31日的地震数据），四川自1970年至2021年7月曾发生过164次M5.0及以上的地震。由于2008年汶川地震余震过于频繁，若使用2008年全部地震数据预测未来发生强震则会导致概率值偏高，因此剔除2008年发生的余震数据。本文使用的数据见表1，共121条数据。

表1 地震数据

本文主要探讨两部分内容：（1）使用1970年至2007年的地震数据，计算两次地震时间间隔（以天为单位），根据计算结果做模型拟合和预测，通过预测2008年发生M5.0及以上地震的可能性从而验证模型选择方法的可靠性；（2）使用表1全部数据用同样的方法预测未来发生M5.0及以上地震的可能性。

1.2 模型介绍

本文分析4种概率分布，首先介绍这4种概率分布的概率密度函数、模型参数（见表2）。

表2 4种概率分布的概率密度函数

（1）指数分布：指数分布是伽马分布和威布尔分布的特殊形式，具有无记忆性，即对随机变量T，有P（T＞s＋t｜T＞t）＝P（T＞s），且（t，s＞0），常用来表示独立随机事件发生的时间间隔，其参数λ表示单位时间内事件发生的平均次数。其在可靠性研究具有广泛应用。

（2）伽马分布：伽马分布的参数α为形状参数，β为尺度参数，当α＝1时，伽马分布为指数分布。龚平等（2001）指出当地震的发生为相互独立事件且仅依赖于时间间隔，与时间起点无关时，可得出地震发生时间服从伽马分布。

（3）对数正态分布：对数正态分布的参数μ为位置参数，σ为形状参数，与正态分布相似，在可靠性研究中，数据若不符合正态分布，则常取其对数使之符合正态分布，因此称作对数正态分布。

（4）威布尔分布：威布尔分布的参数η为比例参数，m为形状参数，当m＝1时，威布尔分布为指数分布。该分布在地震研究中也具有广泛的应用。

1.3 验证模型

本文使用常用的模型选择方法——赤池信息准则（AIC准则）、贝叶斯信息准则（BIC准则）和K-S检验。

AIC可以衡量统计模型拟合的优良性，它建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。AIC定义为式（1）：

式中k为模型参数个数，L为似然函数。从一组可供选择的模型中选择最佳模型时，通常选择AIC最小的模型。AIC为模型选择提供了有效的规则，但也有不足之处。当样本容量很大时，在AIC准则中拟合误差提供的信息就要受到样本容量的放大，而参数个数的惩罚因子却和样本容量没关系，因此当样本容量很大时，使用AIC准则选择的模型不收敛于真实模型，它通常比真实模型所含的未知参数个数要多。

BIC贝叶斯信息准则与AIC相似，可用于模型选择，并且改进了AIC的不足之处。BIC定义为式（2）：

式中k为模型参数个数，n为样本数量，L为似然函数。BIC值越小，说明模型拟合程度越高。

单样本K-S检验是一种拟合优度的非参数检验方法，利用样本数据推断总体是否服从某一理论分布。K-S检验一般返回两个值：D和P值。其中D值表示两条累计分布曲线之间的最大垂直距离，所以D值越小，这两个分布的差距越小，分布越一致。P值是假设检验里面的P值，如果P值大于0.05，那么就不能拒绝原假设，所以P值越大，分布越一致。

2 结果分析

本文首先拟合四川省2008年以前发生M5.0及以上地震时间间隔的概率分布模型，计算参数值，并根据AIC、BIC、D值和P值来检验指数分布、伽马分布、对数正态分布和威布尔分布对地震发生时间间隔的拟合程度，运算结果如表3所示。根据数据的累积概率对应4种分布累积概率绘制p-p plot（见图1），可以直观的看出样本数据是否服从某一分布。由于指数分布的AIC和BIC值相较于其他3种分布偏大很多，说明拟合效果最差。比较伽马分布、对数正态分布和威布尔分布的K-S距离，可以看到在K-S检验中伽马分布返回的D值最小，P值最大。由图1可见，样本数据与伽马分布拟合的较好。因此，选用伽马分布作为四川省2008年以前发生M5.0以上地震时间间隔的最佳拟合分布。

图1 1970年至2007年地震数据4种概率分布P-P plot图

表3 1970年至2007年地震数据建模的拟合检验结果

2008年汶川8.0级地震发生之后，大小余震不断，使用2008年的全部地震数据预测未来并不合理，因此使用剔除2008年余震数据以后的地震数据对四川发生M5.0及以上地震时间间隔的概率分布模型进行拟合检验，运算结果如表4所示。根据数据的累积概率对应4种分布累积概率绘制p-p plot（见图2）。指数分布和对数正态分布未通过拟合检验，伽马分布的AIC、BIC和D值均最小，P值最大，并且通过图2可以直观的看出样本数据与伽马分布更加接近，因此，可以认为伽马分布对四川省1973年以来M5.0及以上地震时间间隔数据的拟合程度最高。

表4 1970年至今地震数据（剔除2008年余震数据）建模的拟合检验结果

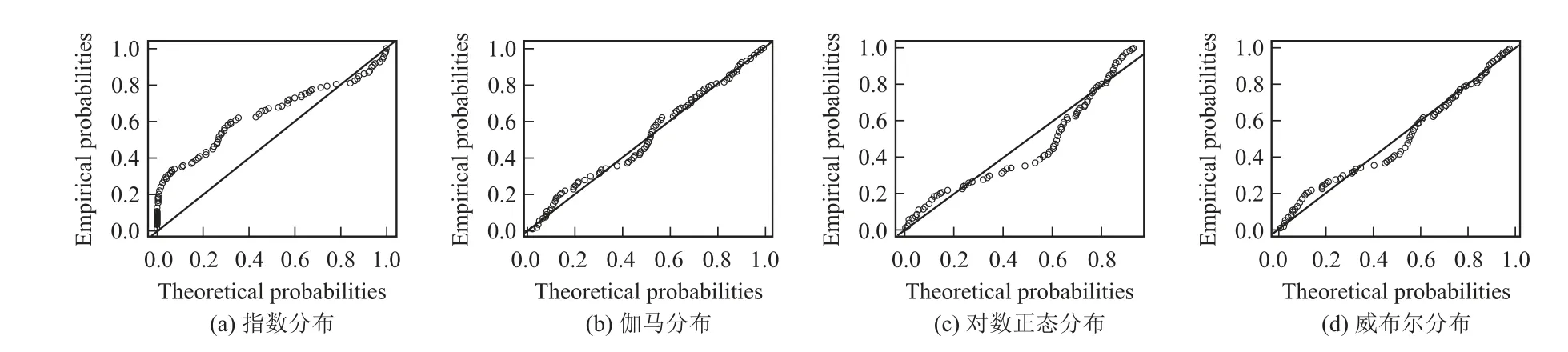
图2 1970年至今地震数据（不含2008年余震）4种概率分布P-P plot图

利用建立的伽马分布对四川的地震危险性进行预测。根据四川2008年以前发生M5.0及以上地震数据求得的伽马分布累积函数（见图3），其横坐标表示地震发生的时间间隔，单位为天；纵坐标表示某一时间地震发生的概率。将上一次发生地震的时间作为坐标原点，则从图中可得出自上一次地震发生之后再发生一次地震的累积概率。由表1可知，在2008年5月12日发生强震的前一次地震在2005年8月5日，从图3可以看到，在2005年8月5日之后2000天中，发生地震的概率随时间的增加而增大，365天（一年）后发生M5.0及以上地震的概率为0.87左右；739天（两年）后发生M5.0及以上地震的概率为0.95左右；预测到在1011天（约2.77年）时，即2008年5月12日发生M5.0及以上地震的概率高达0.98，这与事实基本吻合，说明伽马分布的预测效果较好。

图3 2005年后发生M5.0及以上地震概率曲线

根据上述方法，使用全部样本数据预测未来发生M5.0及以上地震的概率（见图4）。由表1可知，截至2021年7月31日，四川发生上一次强震日期为2020年4月1日，在图4中，设2020年4月1日为坐标原点，可以看到，639天后（即2021年年底）发生M5.0及以上地震的概率大约为0.94，1 004天后（即2022年底）发生M5.0及以上地震的概率大约为0.98，1 369天后（即2023年底）发生M5.0及以上地震的概率为0.99。

图4 未来发生M5.0及以上地震概率曲线

3 结论

本文讨论了1970年至2007年和1970年至今四川地区发生M5.0及以上地震时间间隔的分布及概率预测，得到如下结论：（1）经过拟合检验得出，伽马分布为4种概率分布（指数分布、伽马分布、对数正态分布和威布尔分布）中对四川地区M5.0及以上地震发生时间间隔的最佳拟合。（2）根据1970年至2007年四川发生M5.0及以上地震数据，通过伽马分布预测在2008年会发生M5.0及以上地震，与事实相符，证明模型选取与预测具有可靠性。（3）根据1970年1月1日至2021年7月31日四川地区发生M5.0及以上地震数据（剔除2008年汶川地震余震），利用伽马分布预测未来可能发生地震的概率，得到四川地区2021年发生M5.0及以上地震的概率约0.94，2022年发生M5.0及以上地震的概率约0.98，2023年以后发生M5.0及以上地震的概率趋于1，说明发生M5.0及以上的地震的概率极高。（4）确定最佳的概率模型可以为研究地震提供另一种评估该地区地震危险性的方法。但本研究存在的不足之处在于仅从4种概率分布出发研究地震事件，更适用于对地震预测的初步参考，在后续的研究中可以研究更多概率分布在地震预测上的应用。