被动式激光跟踪测量方法及其误差补偿技术

娄志峰,耿万佳,张记云,林钰琪,范光照,王晓东

(大连理工大学 机械工程学院,辽宁 大连116024)

0 引言

随着智能制造的不断推进和制造业人力成本的不断提升,工业领域中机器代替人工的现象日趋普遍。2018年我国工业机器人的产量达到14.8万台,预计到2022年我国工业机器人的年销售量将超过27万台[1]。工业机器人等装备产量的增加及质量的提升需要制造企业具备高精度、高效率的空间位置测量设备作为支撑。目前,工业机器人绝对位置精度主要采用激光跟踪仪测量。

激光跟踪(Laser Tracking)测量由Lau等人在20世纪80年代发明,Lau等人[2]开展了早期的激光跟踪仪测量误差分析工作,研究了轴系垂直度误差、激光束对正误差等对测量精度的影响。崔成君等人[3]研究了激光光轴与竖直轴的几何误差对仪器测量精度的影响。在激光跟踪测量系统中,测角误差是影响空间坐标测量的主要因素。Ouyang等人[4]采用坐标测量机校准跟踪仪旋转轴的转角误差。Gassneran与Martin[5-6]采用精密转台校准角度测量误差。卢荣胜[7]提出采用自准直仪结合多面棱体对跟踪仪金属圆光栅测角误差进行离散标定。董登峰等人[8]采用谐波分析方法对角度误差进行了修正。

针对激光跟踪仪误差分析与补偿建模方法,Loser与Muralikrishnan等人[9-10]分别提出了带转角镜与无转角镜的两类激光跟踪仪的误差分析模型,并利用长度测量和双面测量法对各项误差进行了分析。Hughes等人[11]对上述模型进行了改进,使得模型中的非线性效应得到了处理。为了将误差补偿方法简化,Conte[12]采用DH建模方法分析了激光跟踪仪的测量误差。周维虎等人[13]推导出了包含激光跟踪仪的主要几何误差的数学模型,并给出了误差的分离和修正方法。对激光跟踪仪的误差机理进行系统地分析与补偿后,其测量精度可以得到很大提升。

经过多年的发展,激光跟踪仪在数控机床、飞机汽车制造、工业机器人等多个领域得到了广泛应用,已经成为现代工业测量中不可或缺的精密仪器,但是由于其跟踪测量系统复杂,研制成本极高,普及到中小型制造企业比较困难。针对上述问题,本文研制了被动式激光跟踪测量系统用于实现工业机器人末端执行器的空间坐标检测。相较主动式激光跟踪仪,该系统具有结构简单,研制成本低、便于普及等优点。对影响被动式激光跟踪测量系统测量精度的主要误差源进行分析,利用多体系统误差建模方法(HTM)建立了该系统的误差分析模型[14]。为了进一步提高被动式激光跟踪测量系统的测量精度,提出将HTM误差分析模型和BP神经网络模型相结合,对被动式激光跟踪测量系统的测量误差进行补偿。

1 被动式激光跟踪测量系统的基本原理

被动式激光跟踪测量系统原理图如图1所示,其主要由二维转台、激光干涉仪和伸缩轴组成。二维转台中的竖直轴与水平轴的回转轴线相交且互相垂直,伸缩轴的轴线经过水平轴和竖直轴的交点且与水平轴的回转轴线相互垂直。构建被动式激光跟踪测量系统的笛卡尔坐标系,二维转台竖直轴的回转轴线作为Z轴;当二维转台方位角示数为0°时,水平轴的回转轴线作为X轴;Z轴与X轴做叉乘得到的向量作为Y轴。

图1 被动式激光跟踪测量系统原理图Fig.1 Schematic diagram of passive laser tracking measurement system

被动式激光跟踪测量系统向测量空间目标位置运动坐标时,伸缩轴前端的标准球通过磁性座吸附在被测目标上。在被动式激光跟踪测量系统运动的过程中,二维转台的竖直轴和水平轴的角度编码器分别对系统的方位角和俯仰角进行测量,激光干涉仪对伸缩轴的位移变化进行测量,从而得到被测目标空间点的球坐标。

2 被动式激光跟踪测量系统的HTM误差分析模型

2.1 HTM误差分析模型的建模过程

当被测目标牵引被动式激光跟踪测量系统运动时,仪器的测量过程可以被分解为整个测量系统绕Z轴旋转θ角度、水平轴和伸缩轴绕X轴旋转φ角度、伸缩轴沿Y轴位移R距离这3个过程。根据齐次坐标变换,可得标准球球心的理想空间坐标为

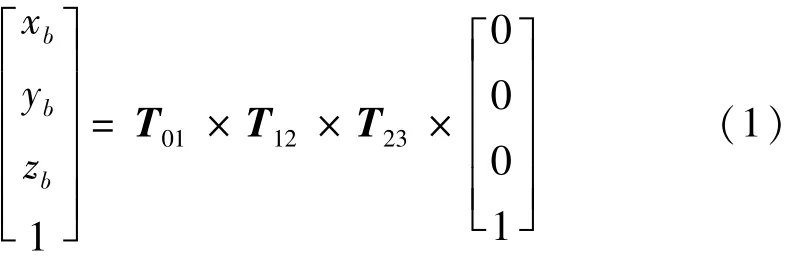
式中:xb,yb,zb分别为标准球的球心在被动式激光跟踪测量系统笛卡尔坐标系中的理想空间坐标;T01为绕Z轴旋转的空间旋转矩阵;T12为绕X轴旋转的空间旋转矩阵;T23为沿Y轴平移的位移矩阵。

式中:θ为绕Z轴旋转的角度。

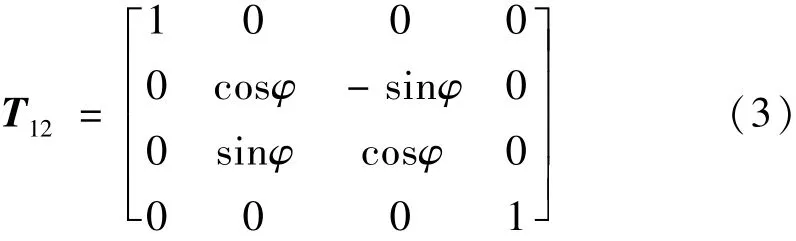
式中:φ为绕X轴旋转的角度。

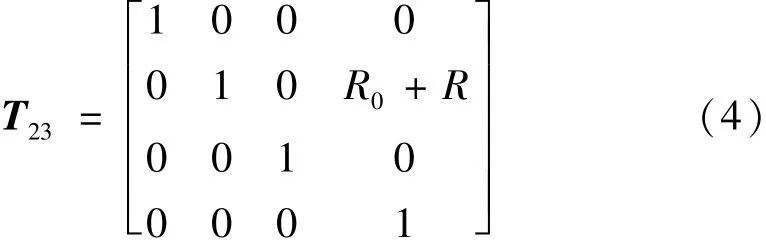
式中:R为沿Z轴的位移距离;R0为伸缩轴的初始长度。

理想情况下,被动式激光跟踪测量系统的竖直轴、水平轴和处于水平状态下的伸缩轴两两之间相互垂直并且相交于测量系统的原点,但是实际上测量系统不可避免地存在着几何误差。测量系统的几何误差如图2所示,主要包括:竖直轴与水平轴存在相对位置与姿态偏移所导致的误差、伸缩轴不经过仪器原点所导致的误差、伸缩轴与水平轴存在的倾斜角度误差以及伸缩轴运动过程中在X与Z两个方向上存在的运动误差。

图2 几何误差示意图Fig.2 Diagram of geometric error

对上述几何误差进行修正,得到标准球球心的实际空间坐标为

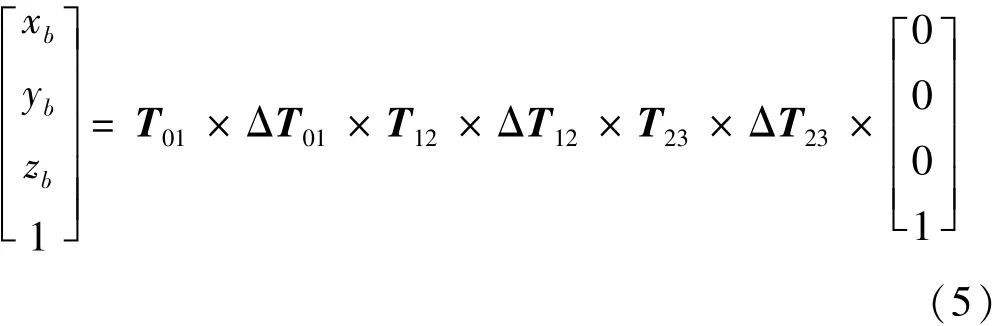
其中,

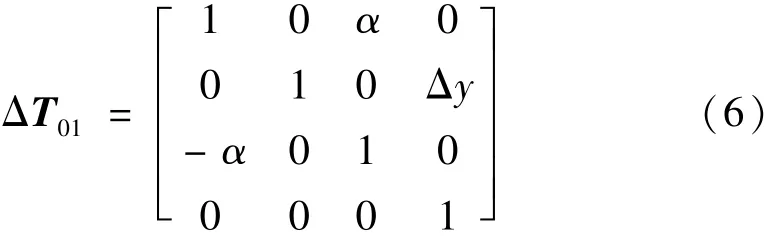
式中:α为水平轴相对于竖直轴的倾斜角度误差;Δy为水平轴相对于竖直轴的偏移误差。

式中:β为伸缩轴相对于水平轴的倾斜角度误差;Δx为伸缩轴相对于竖直轴的偏移误差;Δz为伸缩轴相对于水平轴的偏移误差。

式中:δx为伸缩轴在X方向的运动误差;δz为伸缩轴在Z方向的运动误差。

2.2 被动式激光跟踪测量系统参数及误差测量

2.2.1 水平轴与竖直轴的相对位姿偏差

水平轴和竖直轴之间存在倾斜角度误差α与偏移误差Δy,采用双面测量法对其进行测量,如图3所示。在竖直轴处于0°与180°位置时,将半导体激光器分别固定于水平轴两端,旋转水平轴,记录两种情形下回转激光光斑中心在光电位置传感器(PSD)上的位置[15]。

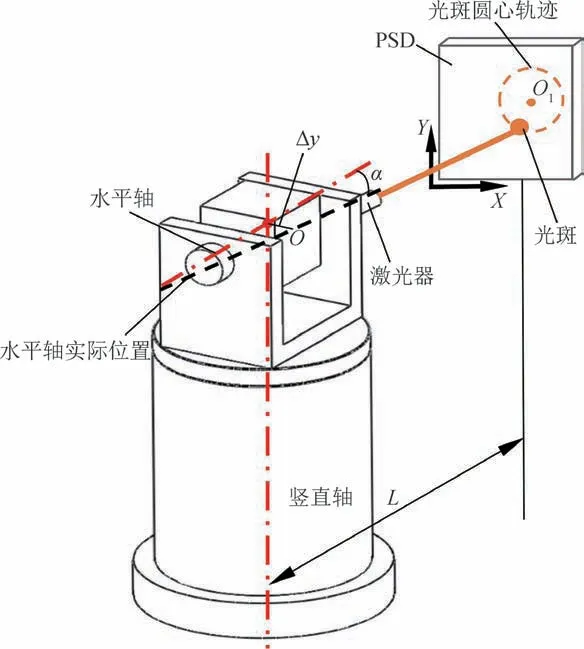
图3 水平轴与竖直轴相对位姿偏差测量原理图Fig.3 Measuring principle diagram of relative pose deviation between horizontal axis and vertical axis

根据上述方法,测得两个光斑轨迹圆心的坐标分别为O1(x1,y1)和O2(x2,y2),计算得出水平轴与竖直轴的偏移误差为

计算得出水平轴与竖直轴的倾斜角度误差为

式中:L为PSD相对于竖直轴的距离。

根据测量结果可知,水平轴与竖直轴的偏移误差为-151.5 μm,倾斜误差为29.5″。

2.2.2 伸缩轴安装偏差

伸缩轴与水平轴、竖直轴之间同样存在倾斜角度误差和偏移误差,采用双面测量法对伸缩轴的安装偏差进行测量。如图4所示,定义此时伸缩轴的姿态为正面,当水平轴和伸缩轴分别旋转180°时,伸缩轴的姿态为反面。利用万分表(型号:SYLVAC 805.8601,最大误差:1.5 μm)分别测量伸缩轴处于初始长度时和伸长ΔL(100 mm)时的双面测量法的测量值。

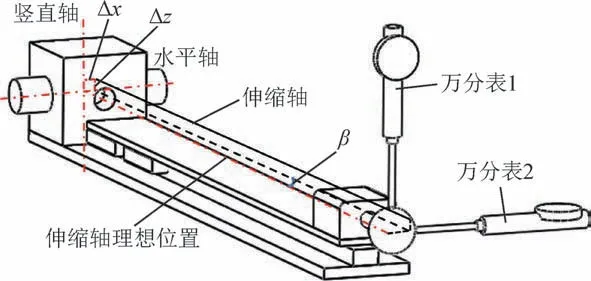
图4 伸缩轴安装偏差的测量原理图Fig.4 Measuring principle diagram of telescopic shaft installation deviation

则伸缩轴的安装偏差为

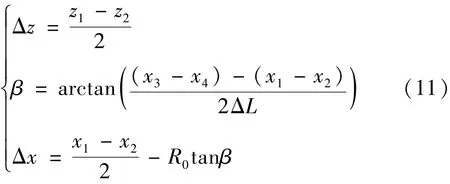
式中:z1和z2分别为万分表1在伸缩轴处于初始长度时的正面测量值和反面测量值;x1和x2分别为万分表2在伸缩轴处于初始长度时的正面测量值和反面测量值;x3和x4分别为万分表2在伸缩轴伸长ΔL时的正面测量值和反面测量值。

实验测得伸缩轴与水平轴之间的偏移误差Δz为167.2 μm,伸缩轴与水平轴之间的倾斜角度误差β为137.6″,伸缩 轴 与 竖 直 轴 之 间 的 偏 移 误 差Δx为-23.1 μm。

2.2.3 伸缩轴运动误差

如图5所示,利用激光准直原理测量伸缩轴的运动误差。在伸缩轴前端安装位置传感器(型号:S5990-01,位置误差为±1 μm),并将半导体激光器垂直对准位置传感器中心,以30 mm为间隔,测量伸缩轴在300 mm范围内的运动误差,测量结果如图6所示。

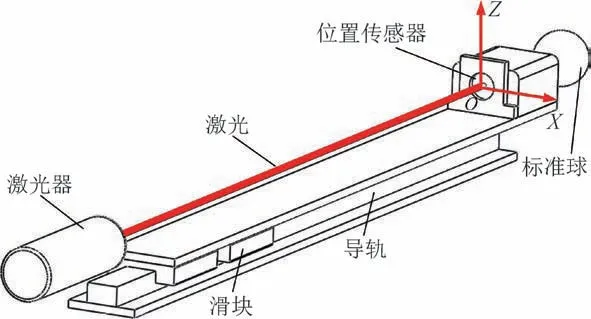
图5 伸缩轴运动误差测量原理图Fig.5 Measuring principle diagram of telescopic shaft motion error

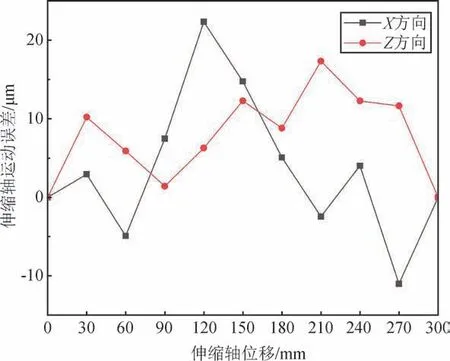
图6 伸缩轴运动误差Fig.6 Motion error of telescopic shaft

2.2.4 伸缩轴初始长度测量

由于激光干涉仪只能测量相对位移,所以当伸缩轴处于初始状态时,标准球球心到测量系统原点的距离(初始长度)无法利用激光干涉仪进行测量。因此需要对伸缩轴的初始长度进行离线测量,原理如图7所示。

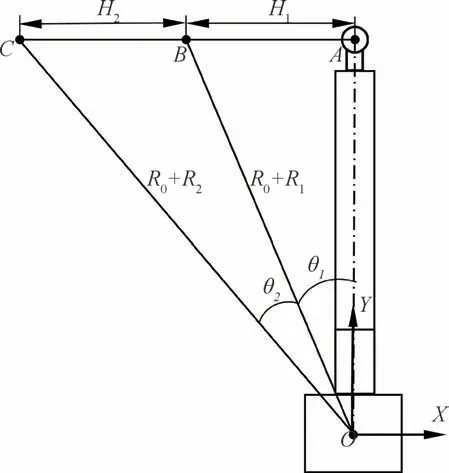
图7 伸缩轴初始长度测量原理图Fig.7 Measuring principle diagram of telescopic shaft initial length

首先将被动式激光跟踪测量系统前端标准球吸附在精密二维运动平台(装置如图8所示,品牌:智泰Ether CAT,型号:EC-10A,最大定位误差:5 μm,最大垂直度误差:6″)上,之后精密二维运动平台带动标准球沿水平轴从A点运动到B点,再从B点运动到C点(A,B,C三点实际位置见图8),调整测量仪器相对于二维平台的位置,使运动过程中仪器俯仰角不变。根据余弦定理可知,△OBC的三边关系为

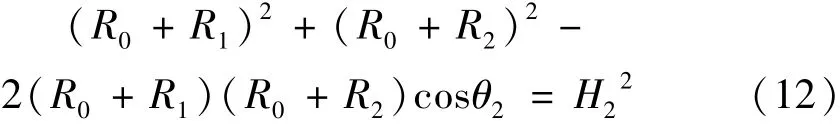
记录R0+R1,R0+R2,H2,θ2的示数,则可根据公式(12)计算出伸缩轴的初始长度为567.468 mm。

2.3 HTM误差分析模型的补偿

将上述系统参数及误差的测量值代入HTM误差分析模型中,对被动式激光跟踪测量系统进行补偿。如图8所示,经过HTM误差分析模型补偿后,采用精密二维运动平台作为标准比对仪器对被动式激光跟踪测量系统的测量精度进行验证。

图8 数据采集实验图Fig.8 Diagram of data acquisition experiment

由于被动式激光跟踪测量系统与精密二维运动平台测量空间的同一点处于不同的坐标系,需要进行坐标转换后进行统一比对。设被动式激光跟踪测量系统和精密二维运动平台测量空间同一点的坐标分别为PA(xa,ya,za,1)和PB(xb,yb,zb,1)。首先将二维平台从原点O开始沿水平轴以10 mm为间隔均匀采取15个点,并根据最小二乘法进行线性拟合得到方向向量nx,将之作为坐标系的X轴,之后将二维平台从原点O开始沿竖直轴以10 mm为间隔均匀采取15个点,并根据最小二乘法进行线性拟合得到方向向量nz。再将nx与nz进行叉乘得到方向向量ny,将之作为坐标系的Y轴。最后,根据公式(13)对PA和PB进行坐标转换。

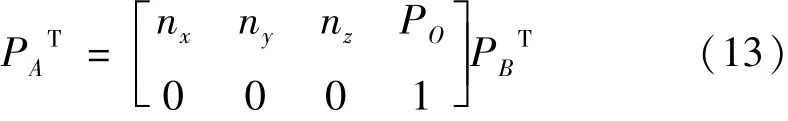
式中:PO为精密二维运动平台的原点在被动式激光测量系统坐标系下的坐标。

对HTM误差分析模型的补偿效果进行验证。将被动式激光跟踪测量系统前端标准球吸附在精密二维运动平台上,精密二维运动平台带动被动式激光跟踪测量系统在140 mm×140 mm平面内以35 mm为间隔均匀测量25个空间点(如图8所示),测量轨迹为:先沿Z轴向上均匀测量5个点,回到最低点后沿X轴运动35 mm,再向上测量5个点,直至25个空间点测量完毕。

在笛卡尔坐标系下,被动式激光跟踪测量系统前端标准球球心的坐标为Pt(xt,yt,zt),比对后的实际坐标为Pa(xa,ya,za),标准球心的空间测量误差为E(xt-xa,yt-ya,zt-za),绝对的测量误差为

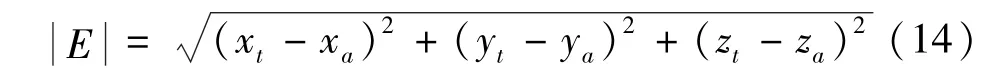
如图9所示,经过HTM误差分析模型补偿后,被动式激光跟踪测量系统的空间坐标测量误差从581.5 μm降低为150.8 μm。

图9 HTM误差分析模型补偿效果图Fig.9 Diagram of compensation effect of HTM error analysis model

3 BP神经网络模型

经过HTM误差分析模型补偿后,被动式激光跟踪测量系统的测量精度得到显著提高,但系统仍然存在残余误差,需要对测量系统的残余误差进行补偿。

BP神经网络对非线性数据有极强的学习能力,为了进一步提高测量精度,本文提出在HTM误差分析模型的基础上,利用BP神经网络模型对被动式激光跟踪测量系统的残余误差进行补偿。如图10所示,将标准球球心的球坐标和被动激光跟踪测量系统的残余误差作为BP神经网络的样本数据集进行训练学习,然后利用HTM误差分析模型与训练好的BP神经网络模型共同对被动式激光跟踪测量系统进行补偿。

图10 HTM+BP神经网络模型流程图Fig.10 Flow chart of HTM+BP neural network model

3.1 BP神经网络模型补偿原理

神经网络是机器学习领域中一种常见的方法。一般情况下,神经网络具有多个且分为三种不同类型的层级:输入层、隐藏层和输出层。每个层级都由一个或者多个感知器组成,相邻层级之间的感知器互相连接。

将标准球球心的球坐标Pt(θ,φ,R)作为BP神经网络模型输入层的输入数据,隐藏层以及输出层中的单个感知器通常会接收多个输入,对输入数据进行处理后再进行输出[16],即

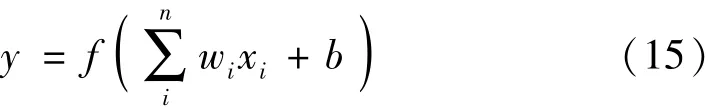
式中:y为感知器的输出;xi和wi分别为感知器的输入和对应的权重;b为感知器的偏置;f为感知器的激活函数,激活函数能够使感知器具有非线性拟合能力,一般为

被动式激光跟踪测量系统经过HTM误差分析模型补偿后,其空间坐标测量误差为E(xt-xa,yt-ya,zt-za)。将E作为BP神经网络模型输出层的目标输出,则每次训练过程中神经网络输出层的总误差为

式中:m为输出层感知器的数量;yk和y′k分别为输出层第k个感知器的实际输出和目标输出。神经网络在训练过程中通过不断优化权重和偏置,降低输出层的实际输出与目标输出的误差。通常利用正则化的损失函数C作为评价指标,即

式中:λ为正则化系数;w为神经网络模型中所有权重的集合。

神经网络在训练的过程中,采用梯度下降法对损失函数进行优化。根据公式(19)对权重w和偏置b进行更新,直至损失函数C的值满足要求。

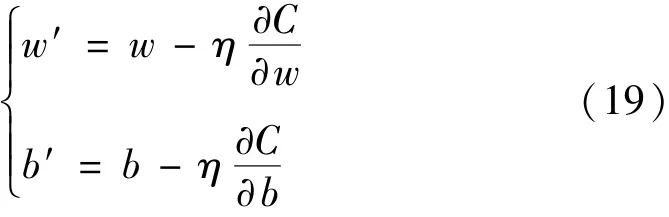
式中:η为学习速率。

利用HTM误差分析模型与训练好的BP神经网络模型共同对被动式激光跟踪测量系统进行补偿,得到测量系统的输出值,即标准球球心的实际坐标值。

3.2 BP神经网络模型的训练

在140 mm×140 mm的平面测量空间内,以10 mm为间隔均匀测量225个空间点作为BP神经网络模型的训练样本数据。多次对神经网络的超参数进行调整,确定BP神经网络的结构以及超参数:模型各层节点数为[3,25,3];学习速率为0.025;正则化系数为1.0。训练过程中BP神经网络模型的损失函数的变化情况如图11所示,损失函数的值在前200次训练时迅速下降,随后下降速度趋于缓慢,接近500次时,损失函数下降幅度极小。在整个训练过程中,训练集损失函数的值略小于测试集,符合一般规律。

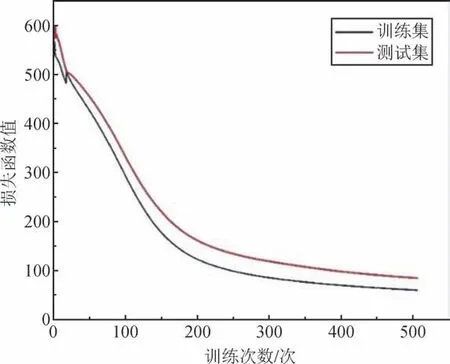
图11 BP神经网络模型训练过程损失函数变化Fig.11 Variation of loss function during training of BP neural network model

4 模型对比与分析

在140 mm×140 mm测量平面空间内再次均匀测量25个空间点,与图8所示的采样点一致。如图12所示,经过HTM+BP神经网络模型补偿后,被动式激光跟踪测量系统的测量误差为51.6 μm,在单一的HTM误差分析模型补偿的基础上,测量误差减小了65.8%。

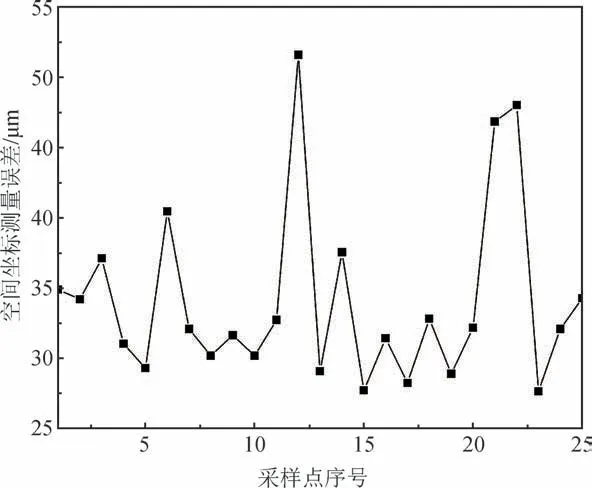
图12 HTM+BP神经网络模型的补偿效果图Fig.12 Diagram of compensation effect of HTM+BP neural network model

5 结论

提出了一种利用被动式激光跟踪测量系统测量空间点坐标的方法,与主动式激光跟踪仪相比,被动式激光跟踪测量系统的测量原理更为简单,研制成本大幅降低,且更便于在工业生产中普及。为了提高被动式激光跟踪测量系统的测量精度,提出HTM+BP神经网络模型对测量系统的误差进行补偿:建立了HTM误差分析模型,对模型的误差参数进行测量后进行补偿;在HTM误差分析模型的基础上,采用BP神经网络模型对测量系统的残余误差进行补偿。经过HTM+BP神经网络模型补偿后,该系统的测量误差降低为51.6 μm,相较单一的HTM误差分析模型,补偿效果提升了65.8%。经过误差补偿后的被动式激光跟踪测量系统可广泛应用于空间运动目标位置精度的测量,提高制造装备测量与加工精度。