线性运动平台多自由度几何运动误差测量技术

蔡引娣,王路辉,高英豪,范光照

(1.大连理工大学 微纳米技术及系统辽宁省重点实验室,辽宁 大连116023;2.大连理工大学 机械工程学院,辽宁 大连116023)

0 引言

线性运动平台在MEMS、芯片制造、生物医疗、集成电路、显微观测等领域得到了广泛的应用[1-3]。随着加工和测量不断向微观领域发展,对线性运动平台的定位精度提出了更高的要求。误差补偿法具有成本低、效率高、效果显著的特点,因此常被用于提高运动平台的定位精度[4-5]。

误差测量技术是误差补偿技术的基础。单一线性轴存在六项运动误差(定位误差、水平直线度误差、竖直直线度误差、俯仰角误差、偏摆角误差、滚转角误差)。为了消除这六项运动误差对运动平台定位精度的影响,需要对其进行高精度测量。传统的测量方法单次只能针对单一误差进行测量,因此测量六项运动误差耗时耗力,且传统测量仪器体积较大,无法集成在运动平台上,也就无法实现在线测量。随着科技的发展,激光多自由度误差测量方法开始兴起,但商用多自由度运动误差测量仪器体积较大、成本高,难以实现在线测量。因此,研究并提出体积小、易集成,且能同时测量多自由度运动误差的方法,对运动平台的误差测量及误差补偿至关重要。

基于激光准直原理和自准直原理,匡萃芳[6]等人提出了一种简便的四自由度误差测量方法,该方法可以同时测量水平和竖直直线度误差、俯仰角误差和偏摆角误差;在此基础上,翟玉生[7]和Huang[8]等人提出了五自由度运动误差同时测量系统,除上述四项运动误差外,还可以测量滚转角误差。激光干涉原理也常被用于测量多自由度运动误差。Gillmer[9]等人提出了一种外差干涉仪,通过对激光器的出射光进行声光调制,再采用差分波前传感技术对干涉信号进行处理,即可得到位移信息和俯仰角、偏摆角误差信息。Hsieh[10]等人将激光干涉原理与激光准直原理和自准直原理相结合,提出了六自由度误差干涉仪测量方法。在上述测量方法中,无论是使用高稳定性的He-Ne激光器,还是低成本的半导体激光器作为光源,都不可避免地存在激光光束漂移。且上述测量方法多采用光电探测器作为误差信号接收器,其灵敏度会受到激光光斑直径和光强大小的影响。此外,在基于双光束检测法的滚转角测量方法中,很难保证双光束的绝对平行。因此,这些测量方法多处于研究和测试阶段,未真正得到实际应用。

针对上述问题,本文提出了一系列线性运动平台多自由度几何运动误差测量方法和测量系统。在这些测量方法中,采用半导体激光器作为测量系统的光源,以减小测量系统的体积,使测量系统可以集成在线性运动平台中,实时在线测量几何运动误差;针对半导体激光器存在光束漂移的问题,提出了一种激光光束漂移主动抑制方法,实时减小光束漂移对测量系统测量准确性、稳定性和重复性的影响;针对激光光斑直径和光强大小对光电探测器灵敏度的影响问题,提出了灵敏度补偿模型;针对双光束平行度对滚转角误差测量准确性的影响问题,提出了平行度误差补偿模型。本文提出的这些多自由度几何运动误差测量系统具有体积小、成本低、易集成等优点,可在精密制造和精密测量设备等领域得到实际应用。

1 多自由度运动误差测量原理与系统

1.1 多自由度运动误差测量系统基本构成

四象限光电探测器(QPD)是一种光电转换元件,由四个性能相同的光电二极管组合而成。其工作原理为内光电效应中的光生伏特效应。在激光多自由度运动误差测量系统中,QPD常被作为光斑位移量的测量元件。

图1 (a)中,当光斑位于QPD的中心位置时,四个光电二极管将输出相等的电流。图1(b)中,当光斑在X轴和Y轴偏离QPD中心位置时,四个光电二极管的输出电流不相等。此时,四个光电二极管的输出电流与光斑偏离位置x和y之间的关系如式(1)所示。

图1 光斑位置示意图Fig.1 Schematic diagram of laser spot position

式中:I1,I2,I3,I4分别为QPD四个光电二极管的输出电流。

为了减小多自由度运动误差测量系统的体积,实现运动误差在线测量,采用半导体激光器作为多自由度运动误差测量系统的光源。下文提到的多自由运动误差测量系统均以半导体激光器为光源,以QPD为光斑位移量测量元件。

1.2 四自由度运动误差同时测量方法

四自由度运动误差同时测量系统原理如图2所示。该四自由度运动误差测量系统由固定端和移动端组成,可以同时测量竖直和水平直线度误差、俯仰角误差和偏摆角误差。由固定端半导体激光器(LD)发射的准直光束经分光棱镜(BS)后分为两束光,透射光和反射光分别进入位于移动端的由四象限光电探测器QPD1组成的二维直线度误差测量模块和由聚焦透镜(FL)与QPD2组成的二维角度误差测量模块。

图2 四自由度运动误差测量系统原理图Fig.2 Principle of four-degree-of-freedom motion error measurement system

当移动端在线性平台上运动时,线性平台的水平直线度误差(δx)和竖直直线度误差(δy)会使准直光束光斑在QPD1上发生沿水平和竖直方向的偏移量Δx1和Δy1。此时,δx和δy可由式(2)计算得到。

式中:kx1,ky1分别为QPD1在X和Y方向上的灵敏度;I1-i(i=1,2,3,4)为QPD1四个光电二极管的输出电流。

当线性平台存在俯仰角误差(θx)和偏摆角误差(θy)时,经FL聚焦后的聚焦光斑在QPD2上会产生沿水平和竖直方向的偏移Δx2和Δy2。此时,θx和θy可由式(3)计算得到。

式中:kx2,ky2分别为QPD2在X和Y方向上的灵敏度;I2-i(i=1,2,3,4)为QPD2四个光电二极管的输出电流;f为聚焦透镜的焦距。

1.3 五自由度运动误差同时测量方法

图3 为线性平台五自由度运动误差测量系统原理图,其中M为平面反射镜,AMM为角度调整架,Beam为光束,PZT为压电陶瓷。该系统在四自由度运动误差测量系统的基础上增加了滚转角误差(θz)测量模块。同时,该系统的固定端加入了1个偏振分光棱镜(PBS)和2个四分之一波片(QWP1,QWP2),用于分光和防止由光学元件表面产生的反射光回射到半导体激光器谐振器内引起光束震荡;移动端增加了1个四象限光电探测器(QPD3),和QPD1组合用于测量滚转角误差。

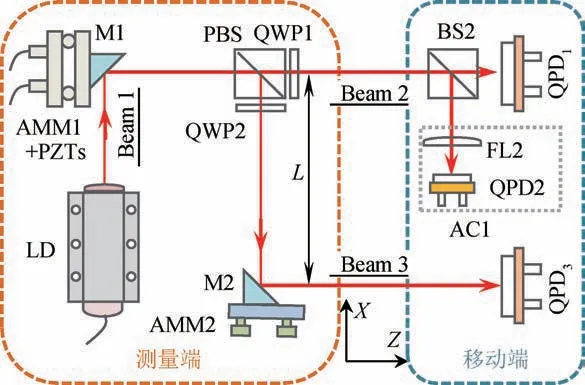
图3 五自由度运动误差测量系统原理图Fig.3 Principle of five-degree-of-freedom motion error measurement system

五自由度运动误差测量系统针对竖直和水平直线度误差、俯仰角误差和偏摆角误差的测量原理与四自由度运动误差测量系统中的测量原理相同,此处不再赘述。本系统采用双平行光束法原理测量滚转角误差,其测量原理如图4所示。当线性平台不存在滚转角误差时,光束2和光束3的光斑将位于QPD1和QPD3的中心处。当线性平台存在滚转角误差时,两个光斑在对应QPD的Y轴方向上会有产生相应的偏移量Δy1和Δy3。由几何关系可得滚转角误差(θz)测量公式如式(4)所示。

图4 双平行光束法原理图Fig.4 Principle of double parallel laser beam method

式中:L为光束2和光束3之间的距离;ky1,ky3分别为QPD3在Y方向上的灵敏度;I3-i(i=1,2,3,4)为QPD1和QPD3四个光电二极管的输出电流。由式(4)可知,θz的分辨力不仅取决于四象限光电探测器的分辨力,还取决于双平行光束之间的距离。

1.4 六自由度运动误差同时测量方法

本文提出的六自由度运动误差测量系统的原理如图5所示。

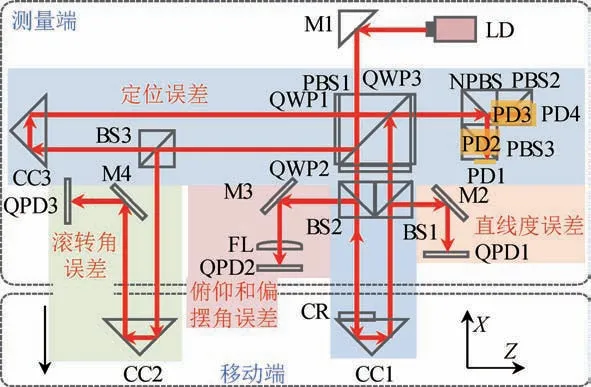
图5 六自由度运动误差测量系统原理图Fig.5 Principle of six-degree-of-freedom motion error measurement system

六自由度运动误差同时测量系统由移动端和固定端两部分组成。移动端由2个角锥棱镜(CC1,CC2)和半透半反膜(CR)组成,无源的设计方式避免了移动端线缆拖拽的问题,满足高速高精度测量场合的应用需求。

由于采用了角锥棱镜和半透半反膜作为直线度误差和角度误差的敏感元件,测量竖直和水平直线度误差、俯仰角误差、偏摆角误差和滚转角误差的分辨力均提高了一倍。

移动端位移量z的测量基于激光干涉原理。从半导体激光器(LD)中出射的光经过45°平面镜(M1)反射,进入偏振分光棱镜(PBS1)后被分成两束光,其中透射光P光为测量光,反射光S光为参考光。P光穿过四分之一波片(QWP2),相位改变45°,之后穿过分光棱镜(BS2)和半透半反膜(CR),经角锥棱镜(CC1)回射,经过分光棱镜(BS1)后再次透过QWP2,此时测量光的相位改变了90°,P光变为S光,并回到PBS1中。PBS1中测量光的偏振态E1为

式中:GQ3,GPBS1-P,GQ1,GPBS1-S为各光学元件的琼斯矩阵参数;E0为激光器发出光的偏振态;i为虚部单位。

S光穿过四分之一波片(QWP1)和分光棱镜(BS3),经角锥棱镜(CC3)回射,再次穿过QWP1,此时参考光的相位改变了90°,S光变为P光,并回到PBS1中,PBS1中的参考光的偏振态E2为

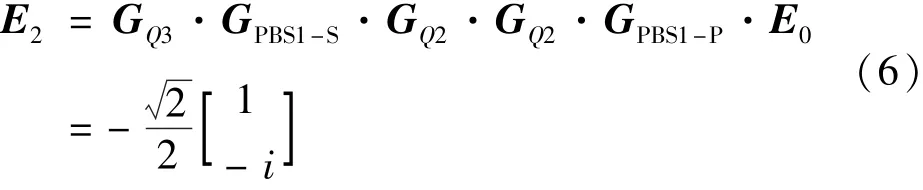
式中:GQ2为光学元件的琼斯距阵参数。

两束光在PBS1内汇聚并形成干涉,再经过由消偏振分光棱镜(NPBS),PBS2和PBS3组成的鉴相模块,将干涉光分成偏振方向依次正交的四束光,分别由4个光电探测器(PD1,PD2,PD3,PD4)接收,其光强信号(IPD1,IPD2,IPD3,IPD4)分别为

式中:A为干涉光的振幅;Δφ为两束光的相位差;t为时间。

当移动端移动Δz时,根据波的叠加原理,光强信号I可以表示为

式中:I0为形成干涉光的光强大小;λ为激光的波长;n为介质折射率。

位移z和相位变化量Δφ之间的关系可表示为

线性运动平台的定位误差Δz可以表示为

式中:d为线性运动平台的系统位移输出量;z为线性运动平台的实际位移输出量。

2 多自由度运动误差测量精度影响因素

在基于半导体激光器的多自由度运动误差测量系统中,半导体激光器的稳定性、四象限光电探测器的灵敏度和双平行光束的平行度将影响多自由度运动误差测量系统的测量精度。下面对各影响因素及解决方法进行具体分析说明。

2.1 半导体激光器稳定性对测量结果的影响

理论上,半导体激光器的出射激光是一条直线,而实际上,由于半导体激光器自身谐振腔热变形、激光器外部固定装置缓慢机械位移、空气各介质折射率不同、大气扰动等原因,激光器的出射激光并非一条直线,存在激光光束漂移。激光光束漂移将影响以半导体激光器为光源的多自由度运动误差测量系统的稳定性、精度和重复性。因此,需要对激光光束漂移进行抑制。

常见的光束漂移抑制方法可以分为主动抑制和被动抑制,被动抑制方法是指将漂移量测量出来,在最终的角度误差和直线度误差中对其进行补偿[11]。但是,偏移量是实时变化的,且多次测量中偏移量是任意的,不具有重复性,所以很难保证补偿后数据的准确性。主动抑制是指采取主动控制的方法将测量过程中产生的漂移量“消除”[12-13],角度误差和直线度误差的测量结果将不会受到漂移量的影响。本项研究提出了一种小型化、易集成、易操作的光漂主动抑制方法[14-15]。为了方便叙述,将提出的光漂主动抑制方法嵌入四自由度误差测量系统中,如图6所示。

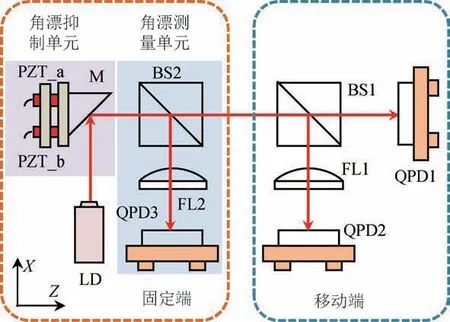
图6 嵌入激光光束漂移主动抑制系统的四自由度运动误差测量系统原理图Fig.6 Four-degree-of-freedom motion error measurement system with an active laser drift compensator

LD的出射激光经反射镜M反射后射入BS2中,反射光射入由FL2和QPD3组成的角漂测量单元,实时测量半导体激光器的角漂。然后将测量得到的角漂量反馈到由精密二维角度调整架、PZT和直角反射镜组成的角漂抑制单元,对角漂进行实时主动抑制。经抑制后,BS2的透射光将不再包含激光光束偏移量,测量得到的四自由度运动误差将不再受光束偏移的影响。

下面对角漂测量和抑制原理进行介绍。当激光器存在X和Y方向角漂Δεx和Δεy时,角漂测量单元中QPD3上的光斑位置会随之发生偏移(ΔxQPD3和ΔyQPD3)。半导体激光器的角漂(Δεx和Δεy)可由式(11)求得。

式中:f2为聚焦透镜FL2的焦距。

根据测量得到的Δεx和Δεy,改变高精度二维角度调整架的角度,使从直角反射镜M反射的光束传播方向产生Δβx和Δβy的变化,从而使反射光平行于理想光轴,如图7所示。

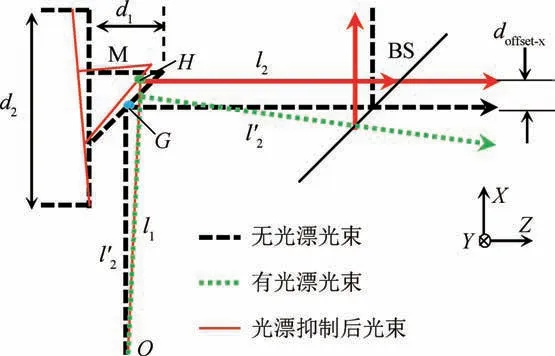
图7 激光光束漂移主动抑制原理图Fig.7 Principle of active compensation of laser drift

设激光出射点为O(0,0,0),当激光器不存在角漂时,出射光线l1与反射镜M的交点为G(l1,0,0)。当激光器发射的激光存在角漂Δεy和Δεp时,l1的方向向量由无角漂时的[1 0 0]T变为[1 ΔεpΔεy]T,此时,出射光线l′1与反射镜M的交点为H。l′1可由以下直线方程表示

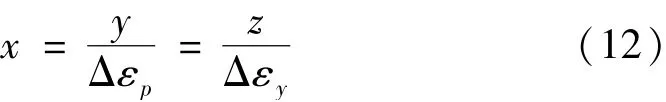
设反射镜M在x,y方向上旋转的角度分别为Δβx和Δβy,消除高阶项后,反射镜M的旋转方程可表示为

因此,反射镜M旋转后,M′的法向量变为

因此,M′与l′1的交点H点的坐标(xH,yH,zH)可表示为

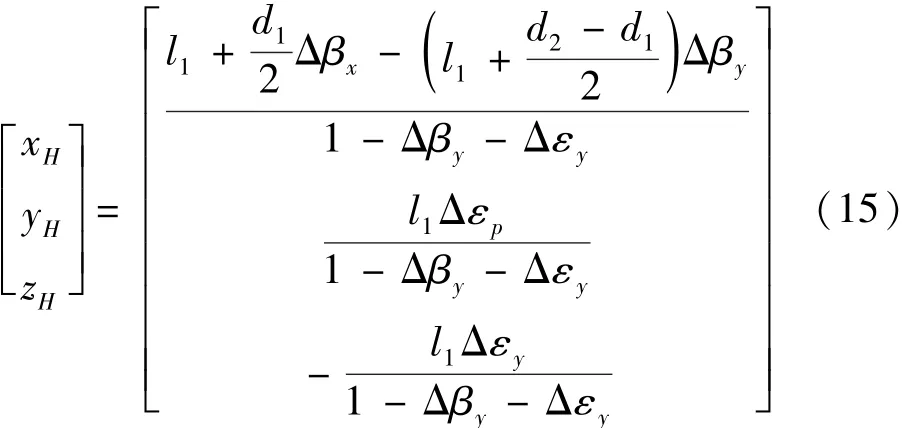
此时,M′反射光线l′2的方向向量为

式中:RM′为旋转后反射镜M′的反射矩阵。

当激光器的角漂被完全抑制时,l′2的方向向量应为

联立式(16)和式(17)可得二维角度调整架转角(Δβx和Δβy)和激光器的角漂(Δεx和Δεy)之间的关系为

需要注意,提出的激光光束漂移主动抑制方法中,由于反射镜M的转动,会引起激光光束与反射镜交点的变化,即点G变为点H,从而使光漂抑制后的光束与无光漂的光束不重合,并在X方向和Y方向存在偏位doffset-x和doffset-y。doffset-x和doffset-y不会影响光束漂移抑制的结果,但是doffset-x和doffset-y将影响四自由度运动误差测量系统中直线度误差的测量结果,所以需要在测量得到的直线度误差测量结果中减去doffset-x和doffset-y带来的影响,其中doffset-x和doffset-y可以表示为

式中:d1为激光器到反射镜M的距离。

图8 为激光光束漂移主动抑制系统控制流程图。系统的角漂测量单元测量得到激光角漂Δεx和Δεy,经I/V转换和放大后输入至采集卡,之后传输至计算机,在计算机中通过PID控制得到PZT的驱动电压,并通过采集卡将驱动电压发送到PZT驱动器,改变PZT的长度,以改变二维角度调整架的角度,实现激光角漂的主动抑制。

图8 激光光束漂移主动抑制系统控制流程Fig.8 Flowchart of control system of laser drift active compensation

激光光束漂移主动抑制系统中,基于PZT的二维角度调整装置制作方法如下:对高精度二维角度调整架的螺纹轴进行钻孔加工,然后将PZT置于孔中,PZT的前端用定位销与二维角度调整架的前端连接,PZT的两根导线从螺纹轴后端的通孔处延伸出来并与供电电源连接。纹轴尾端外部与尼龙套筒固定在一起,以固定PZT。通过PID控制PZT伸长或缩短,从而自动改变二维角度调整架的角度,实现对激光角漂的实时抑制。

将上述激光光束漂移主动抑制系统嵌入四自由度测量系统,研究光漂抑制前后系统的稳定性,测量数据如图9所示。测量端和固定端之间的距离设置为1000 mm,采样时间和采样频率分别设置为30 min和100 Hz。采用巴特沃斯滤波器滤除数据采集过程中噪声信号的干扰。从图9中可以看到俯仰角信号的稳定性从角漂抑制前的2.6 arcsec提高到了角漂抑制后的0.5 arcsec,滚转角信号的稳定性从角漂抑制前的2.8 arcsec提高到了角漂抑制后的0.6 arcsec,证明本文提出的激光光束漂移主动抑制方法可以有效地消除角漂对系统稳定性的影响。

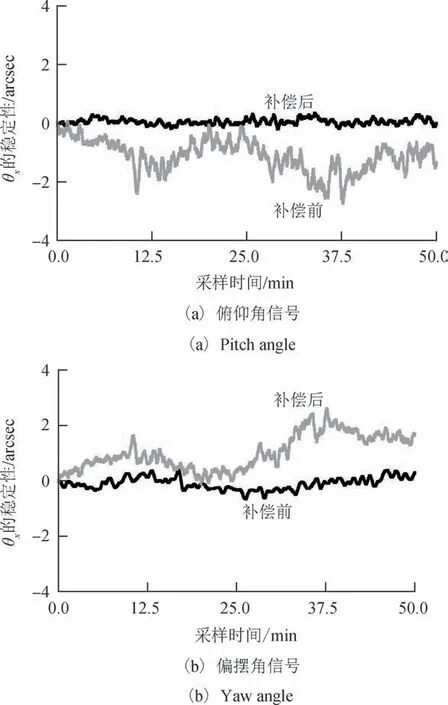
图9 激光光束漂移抑制前后系统稳定性Fig.9 System stability before and after active compensation of laser drift

2.2 灵敏度对测量精度的影响

由水平和竖直直线度误差、俯仰角误差、偏摆角误差和滚转角误差的计算公式可知,四象限光电探测器的灵敏度将影响运动误差的测量精度。用于测量直线度误差和角度误差的四象限光电探测器的灵敏度可以利用高精度位移传感器和角度传感器通过标定实验得到。在测量过程中,通常假设四象限光电探测器的灵敏度固定不变,但是实际上激光器的光强和光斑直径会随着测量距离的变化而变化,这将会影响四象限光电探测器的灵敏度。为了消除四象限光电探测器的灵敏度变化对测量结果的影响,需要在测量过程中对四象限光电探测器的灵敏度进行补偿[14]。

补偿方法如下:首先,采用传统的四象限光电探测器灵敏度标定实验分别标定出移动端位于测量起始位置(do)和测量终点(df)处四象限光电探测器的灵敏度,并定义为kmi_o和kmi_f(其中m=x,y;i=2,3)。通过前期的研究可知,四象限光电探测器的灵敏度与测量距离呈线性关系,因此在任意测量位置处(dm),四象限光电探测器的灵敏度可由式(20)求得。

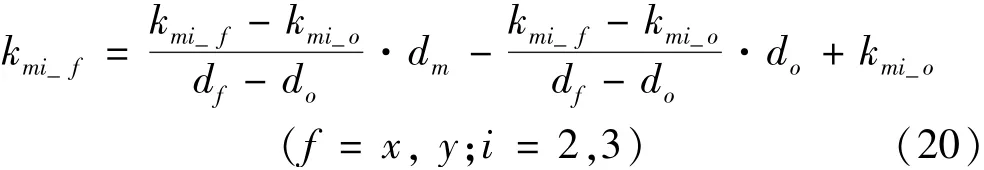
通过式(20)即可消除因激光器的光强和光斑直径随测量距离变化而引起的四象限光电探测器灵敏度误差,进而消除其对五自由度运动误差测量精度产生的影响。

在六自由度运动误差测量系统中,采用三个高精度四象限光电探测器测量水平和竖直直线度误差、俯仰角误差、偏摆角误差和滚转角误差。以六自由度运动误差测量系统中QPD1的灵敏度为例,验证所提出的补偿公式的有效性。

首先,采用Sylvac公司生产的型号为P12D HR的高精度位移传感器分别在测量起始位置(do=80 mm)和测量终点(df=1160 mm)对QPD1的灵敏度进行标定。高精度位移传感器的测量分辨力为0.01 μm,最大测量误差为±0.22 μm。图10是在do和df处标定得到的X方向(kx2_o,kx2_f)和Y方向(ky2_o,ky2_f)QPD2的灵敏度。利用最小二乘法拟合得到的斜率值即为四象限光电探测器的灵敏度。可以看到do处和df处灵敏度不同,这也进一步证明了测量距离的变化会引起灵敏度的变化。do处和df处QPD2X方向的灵敏度(kx2_o,kx2_f)分别为2112.95 μm/V和1683.28 μm/V,Y方向的灵敏度(ky2_o,ky2_f)分别为-1441.56 μm/V和-1093.40 μm/V。

图10 QPD2的X和Y方向的灵敏度Fig.10 Sensitivity of QPD2 in X and Y directional

将图10中标定得到的QPD2在do处和df处的灵敏度代入式(20),即可得到任意位置dm处QPD2的灵敏度km2_f(m=x,y),如图11所示。

图11 QPD2灵敏度造成的测量误差Fig.11 Measurement error caused by sensitivity of QPD2

为了方便比较,采用高精度位移传感器标定出任意位置dm处QPD2的灵敏度km2_c。在之前的研究中,很多学者采用平均法计算四象限光电探测器的灵敏度,即根据do处和df处得到的灵敏度求平均作为QPD2在测量全程中的灵敏度km2_a。将km2_c和km2_a同时画在图11中。由图11(a)可知,计算得到的km2_f与实际测量得到的km2_c很接近。当光斑在QPD2上移动1 μm,由X方向灵敏度kx2_f引起的测量误差ex2_f在2~-15 nm;而由灵敏度kx2_a引起的测量误差ex2_a大约为±112 nm。由图11(b)可知,当光斑在QPD2上移动1 μm,由Y方向灵敏度ky2_f引起的测量误差ey2_f在0~28 nm;而由灵敏度ky2_a引起的测量误差ey2_a在127~-150 nm。由此可知,本研究提出的灵敏度补偿公式可以有效消除由灵敏度变化所造成的测量误差。

2.3 光束不平行对测量精度的影响

在基于双平行光束的滚转角误差测量方法中,双光束的平行度将直接影响滚转角误差的测量精度。在实际测量中,由于光束漂移、机械结构蠕动等因素的影响,很难保证两束测量光束完全平行。本文提出了补偿由不平行光束引起测量误差的方法[14],原理如图12所示。该方法借助商用水平仪完成补偿,在补偿前,将光束2调整至与线性平台的运动轴同轴,即保证在测量起始位置和测量终点位置处光斑始终位于QPD2的中心位置。同样,调整光束3,使其光斑在测量起始位置和测量终点位置处始终位于QPD3的线性测量区域。

图12 双平行光束不平行度引起测量误差的补偿原理Fig.12 Compensation principle of measurement error caused by non-parallelism of doube parallel beams

如图12(a)所示,首先将移动端移动至do处,此时多自由度误差测量系统和商用水平仪测量得到的滚转角误差分别记为θo_R和θo_L。然后,将移动端移动至df处,如图12(b)所示,记录两个仪器测量得到的滚转角误差,分别为θf_R和θf_L。理论上,在两个位置处,由两个测量仪器测量得到的滚转角误差应该是相同的。但是由于两平行光束的不平行度θp的存在,两仪器在测量起始位置(do)和测量终点位置(df)处的输出有如下关系

式中:Δy2_o和Δy3_o分别为QPD2和QPD3在测量起始位置(do)处的输出;Δy2_f和Δy3_f分别为QPD2和QPD3在测量终点位置(df)处的输出。

因此,不平行度θp可以表示为

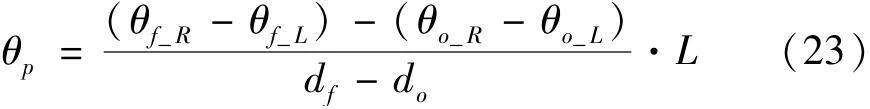
因此,可以通过式(24)来补偿由双平行光束的不平度引起的任意位置dm处的滚转角误差。

式中:θz_R为多自由度误差测量得到的滚转角误差。

用搭建的六自由度误差测量系统测量线性平台的滚转角误差。线性平台的行程为1160 mm,设光束2和光束3之间的距离为120 mm。QPD2和QPD3的分辨力为0.1 μm,因此,六自由度误差测量系统中滚转角误差的理论分辨力应为0.17 arcsec。

同时采用商用水平仪测量线性平台的滚转角误差。商用水平仪的最大测量误差为±0.2 arcsec。图13为滚转角误差测量结果,其中θr-R和θr-L分别为由多自由度运动误差测量系统和商用水平仪测量得到的滚转角误差;θr-C为补偿后的滚转角误差。由图13可知,由于不平行度的存在,多自由度运动误差测量系统和商用水平仪测量得到的滚转角误差存在7.63 arcsec的残差。将测量结果代入提出的误差补偿公式,对多自由度误差测量系统的测量值进行补偿后发现测量残差减小为±1.1 arcsec,证明本文提出的补偿公式可以有效地补偿由不平行度引起的滚转角误差测量误差。

图13 滚转角误差测量结果Fig.13 Measurement results of roll error

3 结论

线性运动平台的多自由度几何运动误差将影响精密制造和测量的准确性。误差补偿技术可以减少线性运动平台多自由度几何运动误差对精密制造和测量准确性的影响。为了提高误差补偿技术的准确性,需要高精度地测量各项几何运动误差。为了实现对线性运动平台多自由度运动误差的高精度、多参数测量,本文根据测量需求,提出了一系列多自由度运动误差测量方法。基于这些测量方法搭建的几何运动误差测量系统具有体积小、精度高和易集成等优点,可以安装在精密制造和测量设备中,实时、在线、高精度地测量几何运动误差,为后续的误差补偿技术提供所需的误差数据。这些测量方法将有效提高线性运动平台多自由度几何运动误差测量的时效性和准确性,为提高精密制造准确性和精密测量准确性提供有力的技术支撑,且具有实际应用价值。未来将进一步开展线性运动平台多自由度几何运动误差测量仪器的研发,以推动我国重要仪器国产化发展。