底水油藏直井临界产量及最佳射孔程度修正式

朱圣举，朱 洁，王思仪，马维云

（1.中国石油长庆油田分公司勘探开发研究院，陕西西安 710018；2.低渗透油气田勘探开发国家工程实验室，陕西西安 710018；3.中国石油长庆油田分公司第六采气厂，陕西西安 710018；4.中国石油长庆油田分公司第八采油厂，陕西西安 710021）

在底水油藏中，当具有一定射孔程度的油井开始生产后，原始油水界面开始呈锥形上升，即形成底水锥进。随着油井产油量的增加，水锥高度逐渐上升，直到产油量达到某一值后，水锥突破，油井见水，则此时的最大无水产油量就定义为临界产量。

Muskat 等［1-5］用各种方法研究了底水油藏直井的临界产量，但均未考虑射孔程度对产量的影响。Abass等［6］考虑了射孔程度后，在二维平面径向渗流条件下，得出最佳射孔程度（从油层顶部开始射孔）为0.5 的结论，但并未考虑底水的半球面向心渗流问题。Guo 等［7］既考虑了射孔程度，又考虑了底水锥进问题，在射孔段部位为平面径向渗流而射孔段下部油层为半球面向心渗流的条件下（见图1），得出均质且各向同性底水油藏直井最佳射孔程度（从油层顶部开始射孔）不大于1/3的结论。

但是，Guo 等的底水油藏直井临界产量计算公式在推导过程中存在如下错误［7］：

式中，H为油层厚度，m；h为射孔厚度，m；Re为采油井的泄油半径，m；φ0为线段与线段的夹角（见图1），（°）。

因为按照假设条件，射孔段以下部分（H-h）为球面向心渗流，即Re，那么，正确的公式应为:

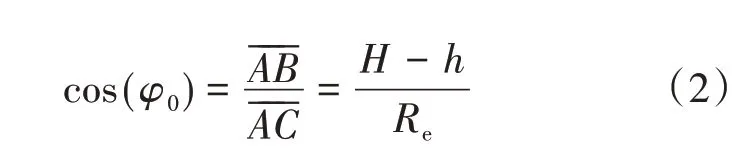
所以原来的底水油藏直井临界产量及最佳射孔程度计算公式需重新修正。然而遗憾的是，这一错误一直未被修正。

蒋平等［8-11］在Guo 等人研究的基础上研究底水油藏直井临界产量时并未考虑cos（φ0）。李春兰等［12-15］在Guo 等人研究的基础上进一步研究临界产量及射孔程度，但并未修正cos（φ0）。

鉴于此，将正确的cos（φ0）代入文献［7］的相关公式进行重新推导、整理，最后得到修正后的底水油藏直井临界产量公式及最佳射孔程度公式，并且首次运用数学解析运算方法，求解了底水油藏直井最佳射孔程度的最大极限值。

1 临界产量公式修正

根据文献［7］，假设油藏均质且各向同性，忽略毛管力及表皮因子，则以稳定渗流为主的底水油藏直井的临界产量为：

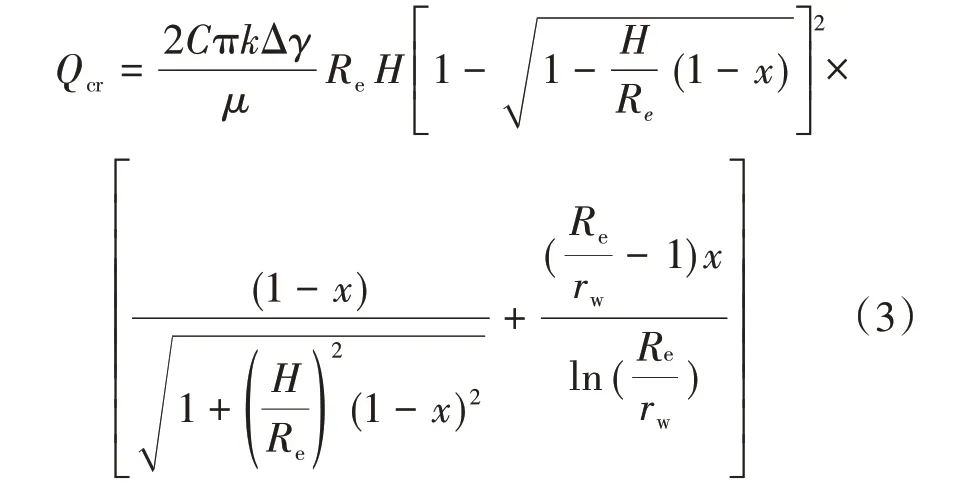
式中，Qcr为临界产量，m3/d；π 为圆周率，无量纲；k为储层渗透率，10-3µm2；μ为地下原油黏度，mPa•s；rw为井筒半径，m；C为系数（0.000 086 4），无量纲；x为射孔程度，无量纲；Δγ 为水油重度差，（g/cm3）•（m/s2）。

其中

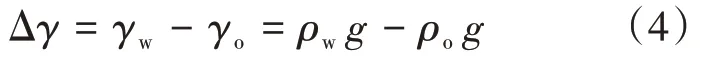
式中，γw、γo分别为水、油重度，（g/cm3）•（m/s2）；ρw、ρo分别为水、油密度，g/cm3；g为重力加速度（9.80），m/s2。

用正确的式（2）代替错误的式（1）后，沿用文献［7］的公式推导方法，则临界产量修正式为：

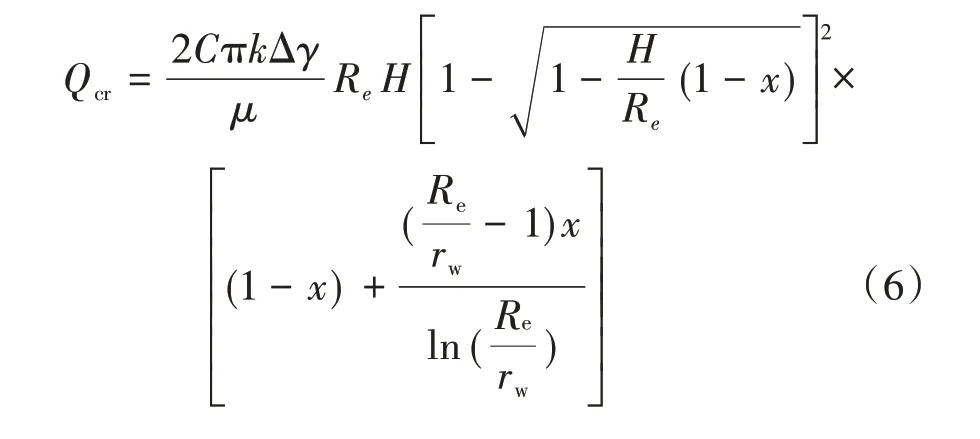
2 最佳射孔程度公式修正

根据文献［7］，底水油藏直井的最佳射孔程度计算方程为：

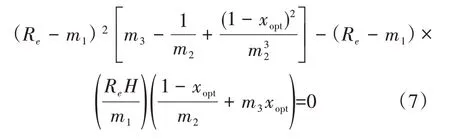
式中，m1为系数，m；m2、m3分别为系数，无量纲；xopt为最佳射孔程度，无量纲。

其中

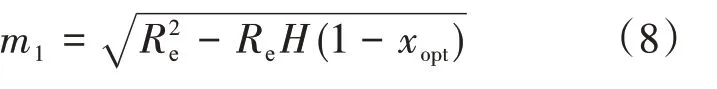
用正确的式（2）代替错误的式（1）后，沿用文献［7］的公式推导方法，则最佳射孔程度修正式为：

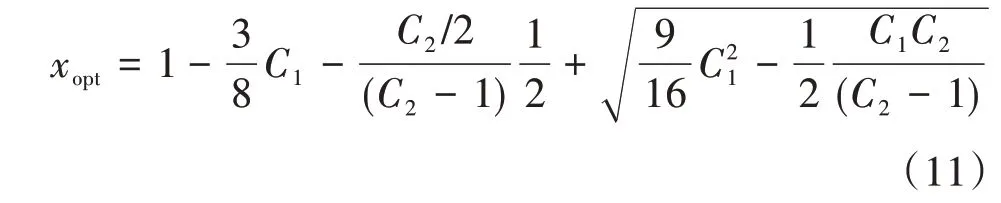
式中，C1，C2分别为系数，无量纲。

其中

3 最佳射孔程度的最大值求解方法

由式（13）可知，在实际油藏条件下，C2＞＞1，因而有

将式（14）代入式（11），得到最佳射孔程度的最大值xoptm：

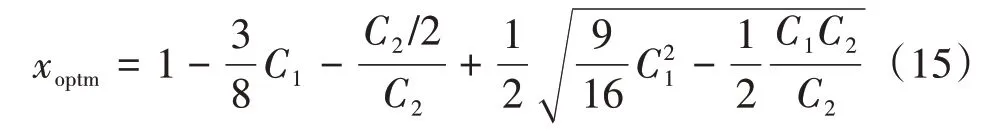
式中，xoptm为最佳射孔程度最大值，无量纲。

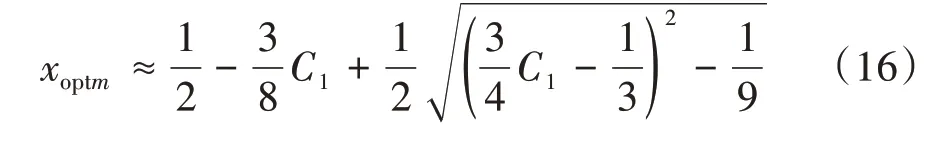
由式（12）可知，在实际油藏条件下，C1＞＞8/9，因而有

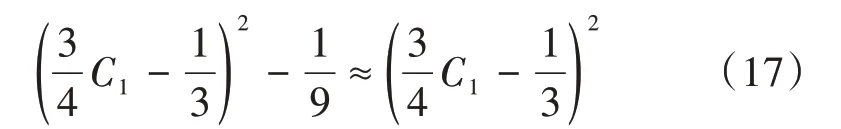
将式（17）代入式（16），得

式（19）表示开采底水油藏直井的最佳射孔程度最大值为1/3。而文献［7］在经过大量的数值计算后，得出开采底水油藏直井的最佳射孔程度最大不超过1/3 的结论。两者结论相近，只不过本文是直接得出解析解，而文献［7］得出的是数值解。

4 实例分析

鄂尔多斯盆地某砂岩底水油藏采用直井开采，具体油藏及油井参数如下：油层厚度H=15 m；储层渗透率k=142×10-3µm2；地下原油黏度μ=2.0 mPa.s；水油重度差Δγ=1.47（g/cm3）•（m/s2）；井筒半径rw=0.1 m。

用上述实际油藏参数分别代入式（3）及式（6），并在Re/H分别为1，5，10的情况下，计算临界产量随射孔程度的变化趋势，结果见图2。

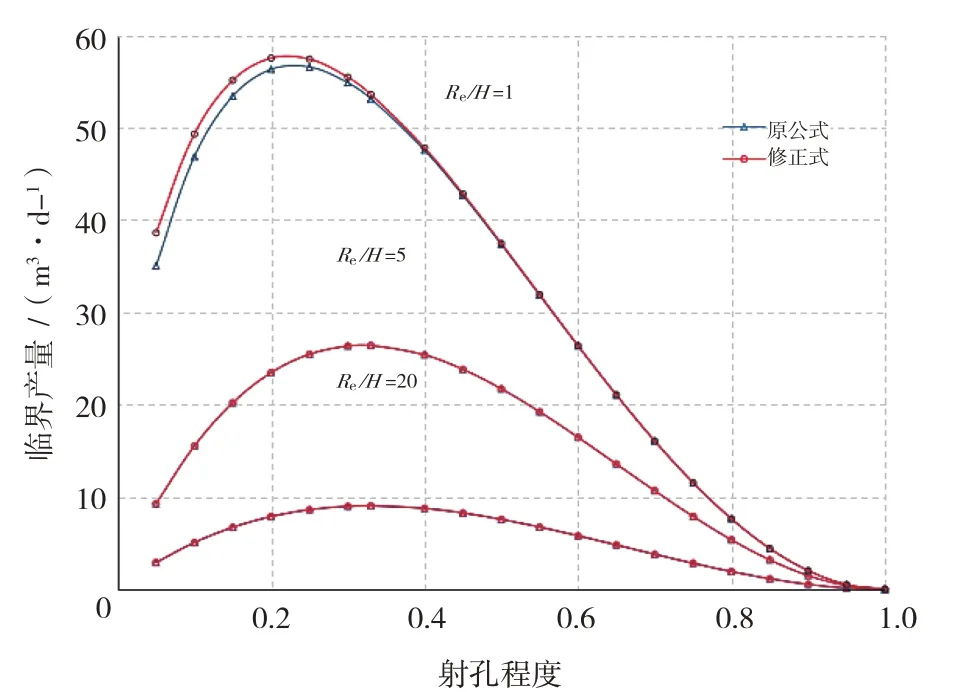
图2 临界产量随射孔程度变化曲线

用上述实际油藏参数代入式（11）中，计算最佳射孔程度随Re/H的变化趋势，结果见图3。

图3 最佳射孔程度随Re/H的变化曲线

由图2可见，修正后的临界产量大于文献［7］的临界产量；两者的差值随Re/H的减小而增大，随射孔程度的减小而增大，最大相对差值可达9.24%。

由图3可见，随着Re/H的增大，最佳射孔程度逐渐增大，但最佳射孔程度最大值不超过1/3。修正后的最佳射孔程度与文献［7］公式计算结果的差值不大，两者的差值随Re/H的减小而增大，最大相对差值为0.96%。

该砂岩底水油藏油层与底水层直接接触，实际开发过程中采用不注水开发，采油井射孔程度均不超过1/3，平均射孔程度0.25，已开发40 a，地质储量采出程度已达到27.9%，综合含水73.4%，开发效果好，预计最终水驱采收率可达到36.2%。

5 结论

（1）修正了底水油藏直井临界产量计算公式中的cos（φ0）。

（2）修正了底水油藏直井临界产量计算公式。

（3）修正了底水油藏直井最佳射孔程度计算公式，且最佳射孔程度可求得解析解。

（4）首次运用数学解析方法，求解了底水油藏直井最佳射孔程度的最大值为1/3，克服了以往运用大量数据进行数值运算的繁琐。