低雷诺数绕丝组件摩擦阻力研究
2021-12-17杜语聪丁常富薛新强
杜语聪, 丁常富, 薛新强
(华北电力大学 能源动力与机械工程学院,河北 保定 071003)
0 引 言
自然循环钠流量决定了其冷却燃料组件的能力,能否有足够的自然循环钠流量将燃料组件衰变余热排出,是钠冷快堆余热排出系统设计的关键问题。自然循环条件下,钠流量的大小由钠流温度差产生的驱动力与自然循环通道的流动阻力共同决定。同时,在钠冷快堆余热排出期间,堆芯流量大约为额定功率的1%~3%,钠流流速很小,燃料组件摩擦阻力成为自然循环回路流动阻力的主要部分。因此准确计算堆芯组件的摩擦阻力对于钠冷快堆非能动余热排出系统设计具有重要意义[1]。
通常研究燃料组件热工水力特性的方法有三种:单通道分析、子通道分析和数值计算模拟。子通道分析法结合了单通道分析和数值计算模拟两种方法,其以棒束组件内子通道为基本计算单元,相比单通道分析方法更全面考虑了反应堆堆芯的实际物理模型,同时相比数值计算又做了一定简化加快了计算速度,平衡了计算准确性和计算速度,能够准确的计算反应堆堆芯内冷却剂的流场、温度场和压力场等热工参数,在钠冷快堆的设计及安全性分析中应用广泛[2]。为了满足钠冷快堆热工水力计算分析需求,不同学者开发出了许多子通道分析程序,如:COBRA-LM、SACROM、MATRA-LMR、THACOS、SUBSC、SABRE4、SUPERENERGY-2和ATHAS-LMR等[2-10]。现有的子通道分析程序中,不同学者对燃料组件摩擦阻力计算采用的经验公式各不相同,比如SSCFR采用了Novendsterm关系式,SUBAC评估了Rehme、Novendsterm、Cheng-Todreas和CRT四种关系式的适用性。现有的燃料组件摩擦阻力研究都是在湍流工况下进行的,少有研究低雷诺数自然循环条件下燃料组件的摩擦阻力,然而在钠冷快堆堆芯余热排出期间,堆芯钠流为自然循环流动,流速很低,钠流保持层流流动,因此研究低雷诺数条件下燃料组件的摩擦阻力是十分必要的。在计算燃料组件的摩擦阻力时,大多数学者采用水模拟实验的方法,通过测量流过燃料组件的水流压降的方法来计算燃料组件的摩擦阻力[11]。然而在堆芯余热排出期间,燃料棒仍有衰减余热加热钠流,燃料棒对钠流的加热与钠流的流动是相互影响的,水模拟实验无法模拟这种自然循环工况。子通道分析法不仅可以将钠作为工质进行模拟,还可以模拟加热情况下钠流在燃料组件内的流动,因此采用子通道分析法可以准确的模拟自然循环工况下燃料组件内钠流的流动和传热。
为了研究自然循环工况下,不同燃料组件摩擦阻力计算公式应用于子通道分析方法时的计算性能,本文将不同摩擦阻力计算公式应用于子通道分析程序中进行模拟计算,分别对比燃料组件摩擦阻力压降、流速分布以及温度分布的计算结果和实验结果,选出了计算性能最佳的燃料组件摩擦阻力计算公式,验证了子通道分析程序的准确性。
1 模型介绍
钠冷快堆一般采用六角形燃料组件,燃料棒在组件盒内以三角形方式排列,每根燃料棒上缠绕有金属绕丝,以加强钠流与燃料棒之间的传热,并保证燃料棒之间的间距[12],其结构如图1所示。子通道分析方法基于控制容积原理,将组件内各个子通道从组件入口到组件出口分割为一系列控制体,在各个控制体上建立流场控制方程,同时设置各壁面边界条件,然后进行迭代计算直至收敛,得到各子通道内部的温度场和流场。因为钠冷快堆堆芯内钠流保持液态,钠流并不沸腾气化,所以在建立流场控制方程时只需考虑钠流的液相状态,从而简化控制方程。
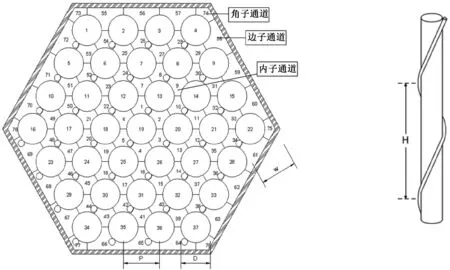
图1 燃料组件以及燃料棒结构Fig.1 Structure of fuel assembly and rod
1.1 控制方程
质量守恒方程的差分形式:
(1)
式中:Ai为子通道i的流通面积,m2;ρn为前一时间步长末工质的密度,kg/m3;mij为工质的轴向质量流量,kg/s;Δx为轴向节点长度,m;m表示与子通道i相邻子通道的编号;wim,j为子通道i流向子通道m的单位长度净横向质量流量,kg/(m·s)。
能量守恒方程的差分形式:
调查发现,学生与导师进行学术讨论的频次大有不同。7%的学生1~3天进行1次学术讨论与交流;40%的学生1周1次;18%的学生每月1次;30%的学生每半月1次;5%的学生表示没有进行过学术讨论。学术讨论是学生向导师进行汇报以及同学间进行学习的好机会,可以及时发现问题并解决问题。诚然,不同年级以及导师对学生的要求不同,也会导致讨论频率不等。
(2)
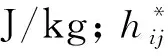
轴向动量方程的差分形式:
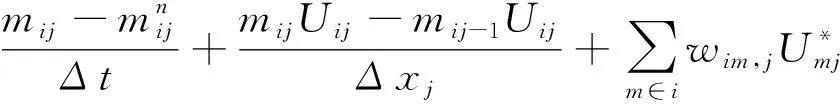
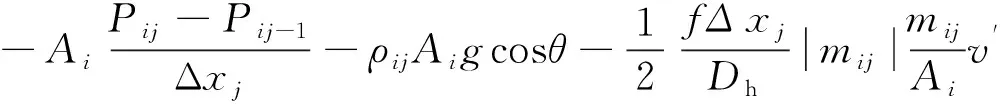
(3)
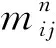
横向动量方程的差分形式:
(4)

1.2 压降模型
钠冷快堆燃料组件的绕丝在加强子通道间冷却剂的交混,强化钠流的换热的同时也使燃料棒的阻力增大,因此需要选择适用于绕丝棒束低流速流动的阻力计算关系式,才能准确计算燃料组件摩擦阻力压降[1]。通过调研得到,常用的针对绕丝棒束燃料组件的摩擦阻力计算关系式有ENG、REH、CTD、CTS、KIR和UCTD等[14-18],详细的计算公式见参考文献,使用范围具体见表1。本文通过将不同的摩擦阻力计算关系式应用于程序计算中,对比实验结果与程序计算结果,分析采用不同关系式对计算结果的影响,选出计算性能最佳的燃料组件摩擦阻力计算关系式。

表1 阻力压降模型的应用范围Tab.1 Application range of resistance pressure drop model
1.3 交混模型
交混系数主要通过实验或者数值模拟得到,表征子通道间钠流交混流动的强度。许多研究表明,交混系数受绕丝和加热棒的直径比和雷诺数的大小影响,随着雷诺数的增大,交混强度增强,交混系数也增大。常用的交混模型如Rowe-Angle、Seale、Rogers-Tahir等[2,19],所覆盖的雷诺数范围均在湍流区,MIT交混模型的适用范围最为广泛,雷诺数适用范围最小为520[6,13]。在钠冷快堆自然循环工况下,钠流的流速很低,雷诺数很小,子通道间的交混作用也很小,因此在本次计算中不考虑计算子通道间的交混。
1.4 横向导热模型
钠冷快堆的主要特征之一是其冷却剂钠有着良好的导热性,不同于常规的压水堆,钠冷快堆堆芯相邻子通道之间的热传导是不可忽视的,因此需要引入横向导热形状系数来准确的计算相邻子通道之间的热传导。当前使用较多的横向导热模型为CTD模型、MA模型和Jeong模型[13,20,21],MA模型主要适用于管状燃料元件,CTD模型主要适用于常规的裸棒状燃料元件,对于绕丝棒束燃料元件,多采用Jeong模型计算,其导热形状系数ε的计算方法如下:
(5)
(6)
1.5 实验模型
实验组件外套管的结构为六角形,内对角距为63.5 mm,内对边距为55 mm,组件内以正三角形方式排列有37根电加热棒代替实际堆芯反应棒,加热棒的直径为7 mm,节径为8.6 mm,加热棒上缠绕有直径为1.5 mm的金属绕丝,绕丝螺距为150 mm。加热棒总长2.7 m,其中入口段为1.2 m、加热段为1.0 m、混合段0.5 m。实验中可以通过调整加热棒的加热功率来改变加热棒的热流密度。加热棒热流密度的计算公式为[16]
(7)
式中:UI为加热棒的加热功率,W;n为组件内加热棒的数量;D为加热棒的直径,m;L为加热棒的长度,m;η为加热棒的加热效率。
实验数据是实验组件自然循环工况下测得的热工参数,实验可以通过调节电加热棒的加热功率来改变燃料组件自然循环工况,并且随着加热功率的升高,钠流的流速和温度也会升高。同时为了使对比结果更具有代表性,本文选取的实验工况为堆芯组件钠流自然循环实验中加热功率较高和较低的两个工况,如表2所示。
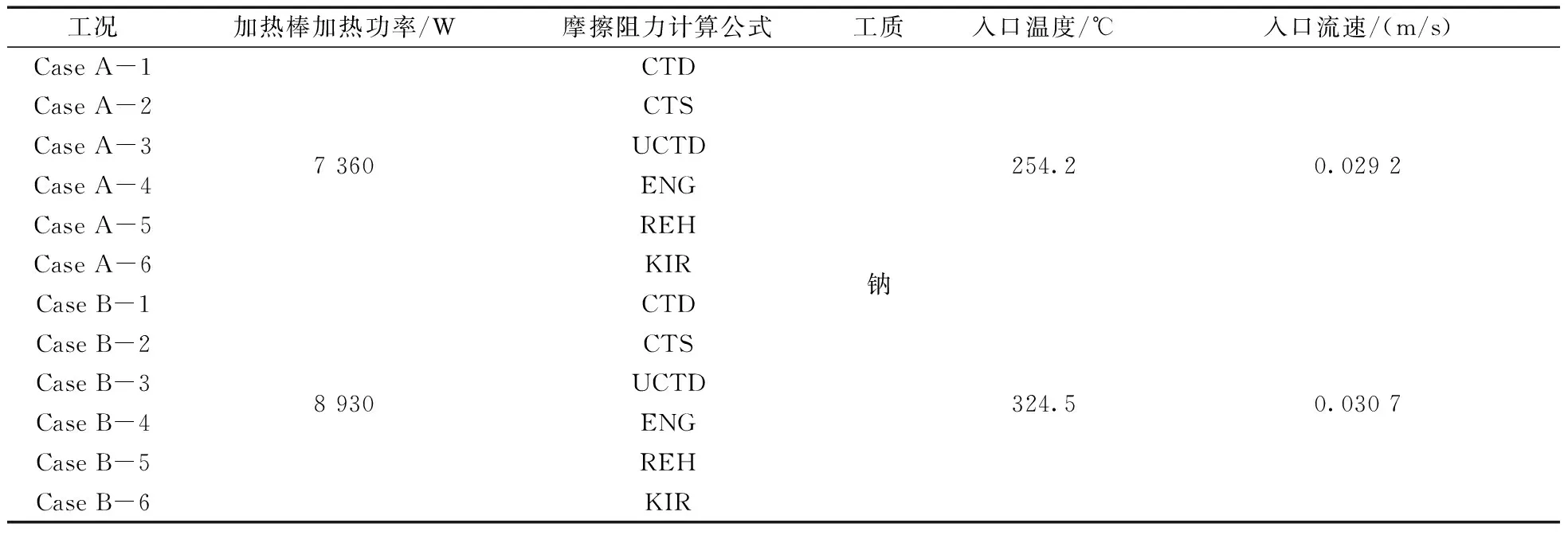
表2 计算工况的参数Tab.2 Parameters of calculation conditions
2 计算结果分析
2.1 压降分析
图2所示为程序分别采用不同压降关系式对实验组件摩擦阻力的计算结果,横轴表示程序计算所采用的摩擦阻力计算关系式,纵轴表示压降的程序计算结果与实验结果的比值。从图中可以看出采用UCTD关系式和ENG关系式后,程序计算的压降结果与实验值吻合较好,采用REH关系式后程序计算结果与实验值相差较大,而采用CTD、CTS以及KIR三种摩擦阻力计算关系式后程序的计算结果十分接近,均低于实验值。整体上看,在高功率工况下,程序采用不同阻力关系式后的计算性能均有所提高,与实验值更为接近。分析认为,在低功率工况下,钠流的流速和温度均低于高功率工况,其雷诺数也较低,而在高功率工况下,雷诺数升高,流动由层流区趋近过渡区,阻力关系式的准确性都有所提高,因此在高功率工况下程序计算结果的准确性高于低功率工况下的计算结果。因此认为在低雷诺数流动工况下,UCTD关系式和ENG关系式的准确性较好,其中UCTD关系式的准确性最好,且随着雷诺数的提高,各个关系式的摩擦阻力计算性能也会提高。

图2 压降分析Fig.2 Analysis of friction pressure drop
2.2 流速分析
图3所示为不同工况下程序采用不同摩擦阻力计算关系式后的流速计算结果与实验数据的比值。从图3中可以看出,程序采用不同摩擦阻力计算关系式后的计算结果与实验数据基本吻合,误差均控制在2.5%以内,因此在自然循环工况下,采用不同摩擦阻力计算关系式对流速计算结果的影响很小。从图3(a)中可以看出,在较低功率工况时,程序采用ENG计算关系式后的计算结果在不同高度处都有这良好的准确性,而采用其他计算关系式后程序的计算结果在2.5 m高度处与实验数据存在较大的误差。从图3(b)中可以看出在较高功率工况时,只有程序采用KIR计算关系式后在2.5 m高度处的计算结果与实验数据存在较大的偏差。随着加热棒加热功率的升高,采用CTD和UCTD计算关系式后程序的计算结果与实验数据更为接近,计算准确性有所提高;程序采用CTS和ENG计算关系式后的计算结果与实验数据的比值变化很小。因此可以认为,程序采用CTD、UCTD和KIR计算关系式后的计算准确性受实验工况的影响,随着加热棒加热功率的升高,钠流流速和温度的升高,CTD和UCTD关系式的计算性能也会提高,KIR关系式的计算性能反而下降。结果表明,采用不同摩擦阻力计算关系式,对程序的准确性影响较小,计算结果与实验数据误差不超过5%,其中CTD、CTS和UCTD关系式表现出良好的计算性能。

图3 流速计算结果与实验值的比值Fig.3 Ratio of calculated velocity to experimental value
2.3 温度分析
图4所示为7 360 W工况下不同高度处子通道温度分布的计算结果。从图4(a)和(b)中可以明显看出从绕丝组件中心向外的温度梯度,与实验值的趋势基本一致。程序采用CTS计算关系式后的计算结果与程序采用CTD计算关系式的计算结果相比,CTS模型对内子通道温度的计算值较高,而CTS模型对边角子通道温度的计算值较低,这是由于两种模型对三种不同子通道摩擦阻力系数的计算不同导致的。程序采用UCTD、KIR和ENG三种摩擦阻力计算关系式后程序的计算结果十分接近,与实验数据基本吻合。从图4(c)中可以看到,采用不同摩擦阻力计算关系式后程序的计算结果与实验数据相差不超过2 ℃,证明了程序的准确性。CTS模型计算值低于实验数据,CTD、KIR、ENG三种模型计算值高于实验数据,程序采用CTD模型后计算值与实验数据基本一致,证明了UCTD关系式有着良好的计算性能。
图5所示为8 930 W工况下不同高度处程序采用不同计算关系式的温度分布计算结果。从图5(a)中可以看到,程序采用不同计算关系后的计算结果有着相同的趋势,但在24号子通道处存在较大的误差,在其他子通道处,计算结果与实验数据十分接近,认为可能是随着加热功率的升高,绕丝组件内钠流的雷诺数升高,流体内部产生的交混导致的,雷诺数的增大使子通道间的交混作用影响变得明显,导致内子通道处计算结果存在偏差,认为随着雷诺数的升高,子通道间钠流的交混流动作用不可忽略。结合图4和图5可以看出,摩擦阻力计算关系式的采用对程序温度分布的计算结果影响较小,程序计算结果呈现相同的趋势,与实验数据的偏差较小,误差不超过4 ℃。在1.5 m高度处,采用不同摩擦阻力计算关系式后程序的计算结果在内子通道处偏差较大,在边角子通道处的计算结果十分接近。从结果上看,采用UCTD摩擦阻力计算关系式时,程序的计算结果与实验数据最为接近,因此认为低雷诺数自然循环工况下,UCTD摩擦阻力计算关系式有着较好的计算性能。
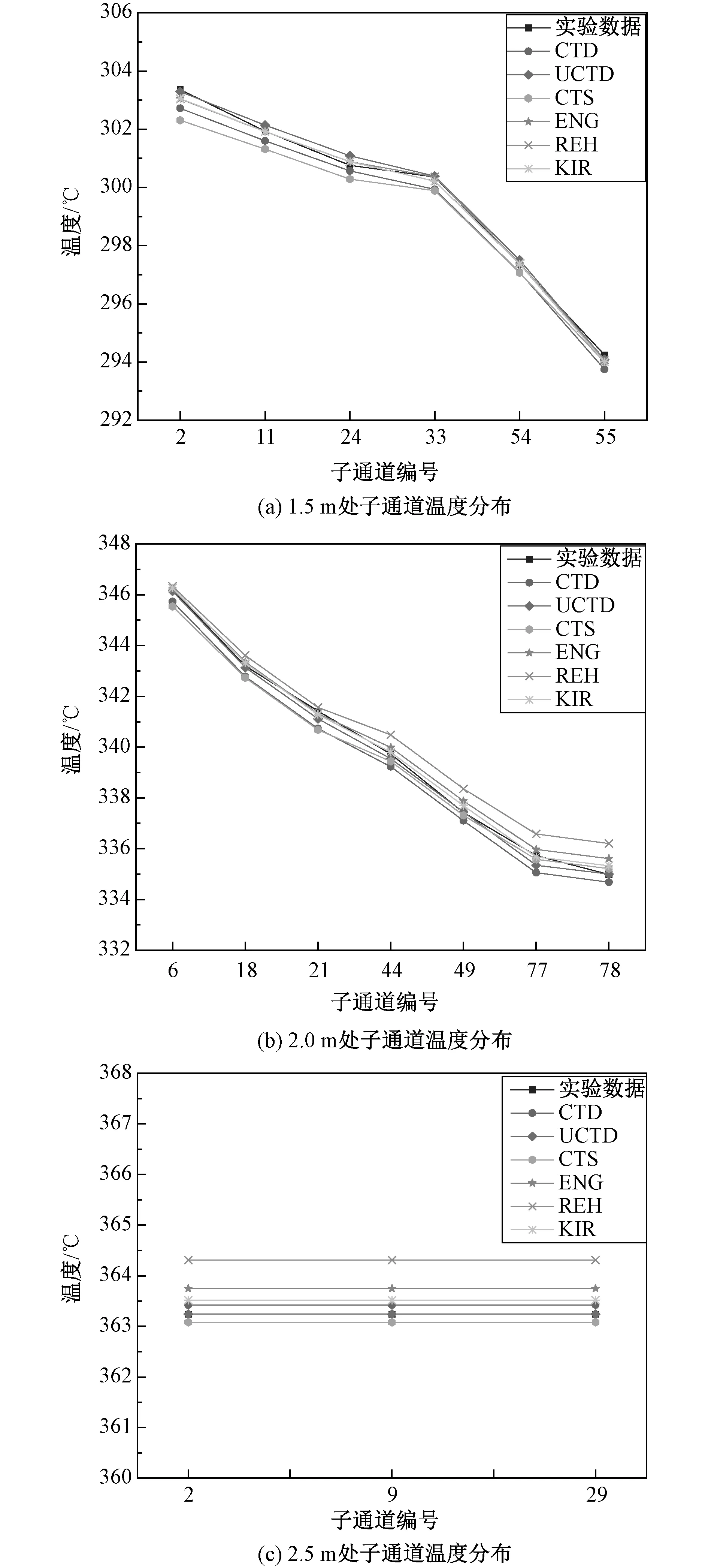
图4 7 360 W工况下温度分布计算结果Fig.4 Calculation results of temperature distribution at 7 360 W

图5 8 930 W工况下温度分布计算结果Fig.5 Calculation results of temperature distribution at 8 960 W
3 结 论
本文利用钠冷快堆子通道分析程序,基于37棒绕丝组件模型,将不同阻力关系式应用于程序对实验组件进行模拟计算,将程序计算结果与实验数据进行了对比分析,结果表明:
(1)随着绕丝组件加热棒的加热功率升高,钠流雷诺数升高,各摩擦阻力计算关系式的计算性能均有所提高。
(2)自然循环工况下,摩擦阻力计算关系式的选用对流速分布和温度分布计算结果的影响较小,对压降计算的影响较大。
(3)当绕丝组件内钠流的雷诺数升高到300以上时,钠流内部的湍流交混作用不可忽视。
(4)针对钠冷快堆低雷诺数自然循环工况,UCTD摩擦阻力计算关系式具有较好的准确性。
