复合绝缘子水珠模型的起晕和闪络电压影响因素及机理分析

2021-12-17律方成牛雷雷王胜辉姜婷玥郭佳熠

华北电力大学学报(自然科学版) 2021年6期

律方成，牛雷雷，王胜辉，姜婷玥，李伟，李浩，郭佳熠

(1.华北电力大学新能源电力系统国家重点实验室，北京 102206；2.华北电力大学河北省输变电设备安全防御重点实验室，河北保定 071003；3.国网保定供电公司，河北保定 071003)

0 引言

复合绝缘子因具有质量轻，体积小，憎水性能好，防污闪等优点而被广泛应用于电力系统[1-3]。而复合绝缘子电场分布受毛毛雨、雾等恶劣天气下的表面形成的水珠影响而改变，引发表面电晕放电甚至污闪[4，5]。另外，放电过程中产生的臭氧等副产物会加速硅橡胶的老化和绝缘性能的进一步下降[6-8]，因此，亟需开展复合绝缘子表面水珠的电晕放电及其影响因素的研究。

国内外研究学者对水珠起晕电压及其影响因素进行了相关研究。文献[9]分析了水滴参数在不同电场旋转角的作用下对水珠表面电场的影响,探究了降落水滴对空间电场及闪络特性的影响。文献[10]分析了硅橡胶表面存在分离水珠时的运动特性和局部放电数据，处理得到了水珠闪络电压特性。文献[11]基于伞裙和芯棒处存在水珠的两种不同情况，提出了两种研究模型。文献[12]和[13]采用可见光成像、RIV无线电干扰方法和平板电极研究模型，分析了水珠体积和个数对RTV试品的起晕电压特性的影响。文献[14]试验研究了在DC/AC电场下的运动过程和闪络电压特性，并采用电液耦合的方法建立了仿真模型。上述文献主要依靠可见光信号作为电晕起始判据，无法定位放电位置，试验结果受试验人员的经验影响较大，对水珠与起晕、闪络电压的关系及其机理研究较少。

本文提出了伞裙和芯棒研究模型，采用强电解质水溶液理论分析了不同NaCl添加量的水珠的相对介电常数变化，并在静电场假设下对模型电场和起晕电压变化特性进行了理论分析和试验研究；采用有限元法仿真研究了水珠体积和位置对伞裙和芯棒模型电场特性的影响；搭建了日盲紫外成像试验平台，研究并验证了不同水珠参数对模型起晕和闪络电压的影响。为优化绝缘子结构设计和水珠起晕的屏蔽措施提供理论指导。

1 仿真和试验方法

1.1 水珠自然分布及建模

图1展示了绝缘子表面水珠分布情况。

图1 复合绝缘子水珠分布Fig. 1 Water droplet distribution of composite insulator

图1中，绝缘子电场特性随表面水珠位置变化而改变，本文根据水珠和绝缘子的接触面与电场线之间的关系，将研究对象分为芯棒模型和伞裙模型[11]，前者的电场线平行于水珠、绝缘子接触面，而后者电场线垂直于水珠、绝缘子接触面。

伞裙和芯棒试验研究模型如图2所示。

图2 伞裙和芯棒模型Fig. 2 Model of sheath and shed

图2中，伞裙和芯棒研究模型均采用圆形铝板电极模拟水珠和绝缘子的接触面与电场线之间的关系，铝电极的厚度为12 mm，直径为30 cm。采用试验硅橡胶样片模拟伞裙和芯棒，样片尺寸为45 mm×45 mm×5 mm。

1.2 试验接线和试验方法

试验接线如图3所示。

图3 试验接线示意图Fig. 3 Schematic diagram of the test connection

图3中，工频交流电源为YDTW-10/110，采用CoroCAM504紫外成像仪连接视频采集卡记录紫外放电信号，电导分析仪为sx713，采用微升注射器和游标卡尺对水珠的体积和位置进行精确测量。采用0.08 mL，0.14 mL，0.18 mL三种水珠体积[12]表征不同工况下的水珠情况，根据等值盐密和污秽度、电导率的换算方法[12]将水溶液分为4类，对应关系如表1所示。

表1 水溶液的电导率及其污秽程度Tab.1 Contamination level and conductivity of water solution

按照Debye和HÜckel提出的强电解质水溶液理论，水中添加不同剂量的NaCl会改变溶液的相对介电常数，文献[15]给出的经验如式(1)所示。

D=D0(1-αy)

(1)

式中:D为添加溶剂之后水的相对介电常数；D0为去离子水的相对介电常数，对于NaCl而言，稀释系数α取6.6，y表示溶剂添加量，单位为摩尔。

采用逐步升压法判断起晕电压，电压步长为0.5 kV，取5次观测的平均值。本文利用紫外成像仪判定电晕起始电压和放电位置，当固定位置出现放电光斑，且光子数大于8[16-18]，即判定该电压为起晕电压。

1.3 仿真模型及参数

依照图2中的伞裙和芯棒模型及其尺寸，采用COMSOL Multiphysics仿真研究了水珠电导率和介电常数对水珠电场分布的影响，芯棒模型仿真模型如图4所示。

图4 芯棒水珠仿真模型Fig. 4 Simulation model of water droplet of mandril

由于水珠起晕时施加电压相对较低，本文忽略电流效应，采用电场分布仅与介电常数有关的静电场假设[19]；随着施加电压提高，泄漏电流增大，采用电流场考虑水珠的介电常数和电导率来分析模型的闪络电压[20]。

高压电极施加电压为37 kV，极间距离为45 mm，接地电极和空气为零电位，参数设置如表2所示。

表2 仿真材料及其参数Tab.2 Simulation materials and their parameter

定义了电场的畸变程度系数Kdis，如公式 (2)所示。

Kdis=Emax/Eavg

(2)

式中：Emax为附着水珠后绝缘子最大场强；Eavg为正常绝缘子平均电场。

2 水珠模型影响因素及机理仿真研究

2.1 电导率和相对介电常数的影响机理

采用数值计算模型和强电解质水溶液理论，分析了不同NaCl添加量水珠的相对介电常数变化。不同污秽程度下水滴的电导率的变化与电场畸变程度的关系，如公式 (3)～(10)所示。

(3)

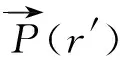
(4)

公式(4)是散度定理，其中▽是Nabla算子。面电荷和体电荷密度的计算如公式 (5)和(6)所示。

(5)

(6)

在散度定理的基础上，将公式(5)～(6)代入公式(3)，得到场点电场强度计算公式如式(7)。

(7)

(8)

(9)

式中：y为水珠中溶解的NaCl摩尔数，单位为摩尔；ε0表示真空介电常数。

整理可得:

(10)

公式(10)右侧的第一项为外部电场，第二项和第三项为溶解了强电解质之后的水珠边缘附加电场，其中第三项随着NaCl摩尔数y的增加而减小，降低水珠周围电场强度。造成电场强度下降的原因是，在水溶液中，水会围绕在离子周围，形成水化离子，水化的结果减少溶液中自由水分子的数量，增加离子体积，使离子附近水偶极子对离子定向，破坏水层的四面体结构，外界施加电场一定时，水中溶解的氯化钠摩尔数改变这部分水溶液的介电常数[21，22]。

2.2 水珠电导率和介电常数对电场的影响

在公式(9)的基础上，仿真分析了水珠电导率和相对介电常数对电场强度的影响，分别对应于模型的起晕电压和闪络电压。以伞裙模型为例，仿真结果如图5所示。

在图5(a)的中，随着水珠相对介电常数降低，边侧最大电场强度降低了9.6%。由公式(9)可知，随着水中溶解NaCl摩尔数的增加，水珠介电常数降低。在静电场中，水中溶解的氯化钠摩尔数增加降低了水珠的相对介电常数，等效改善了电场分布，从而相对提高了模型的起晕电压；

由图5(b)可知，水珠电导率的提高引起的电场畸变程度提高了48%。在50 Hz电流场中，水珠电导率增大提高了模型的泄漏电流，等效加大了电场畸变程度而使闪络电压降低。

图5 电导率与电场分布的关系Fig. 5 The relationship between electric conductivity and electric field strength

2.3 水珠起晕位置机理分析

本节在静电场假设下的电介质极化机理，分析了水珠的附着位置对起晕位置的影响，如图6所示。

图6 模型形式与电场强度Fig. 6 Model and electric field strength

在伞裙模型下，水珠在外加电场的作用下发生极化。以极板电极为负半周为例，如图6 (a)所示，水珠顶端出现正电荷积聚现象，导致该处电场发生畸变，当电场的畸变程度达到使空气产生自持放电阈值时，该处便产生电晕放电现象。

同理，芯棒模型下的水珠如图6(b)所示，同样以极板电极为负半周为例进行分析，此时，水珠在外加电场的作用下的极化效应产生的电场畸变主要发生在水珠边侧，即水珠、空气、硅橡胶三交叉点处，且随着外加电场的增加而加剧。不考虑水珠运动的情况下，当外加电场达到一定程度时，三交叉点处的场强达到空气放电阈值，产生稳定的电晕放电现象。

2.4 水珠距离和数量对电场分布的影响

为研究水珠距离和数量对电场强度的影响，使施加电压恒定，调整水珠距离高压侧的距离和个数，分析了硅橡胶和水珠接触面电场分布及其畸变程度，仿真结果如图7所示。

图7 水珠数量和绝缘距离对电场强度的影响Fig. 7 The influence of number of water droplet and insulation distance on electric field strength

由7(a)中可知，当水珠距离接地电极的距离De从大到小的变化时，水珠与硅橡胶接触面上的面最大电场强度先减小后增大。而当水珠位于硅橡胶中间位置时Emax=16.71 kV/cm，水珠与电极之间的距离会改变模型的电场分布。

对比图7(a)和图7 (b)可知，当只有单个水珠时，最大电场强度为22.94 kV/cm, 而在De=0.2而水珠数量为2时，模型最大电场强度为23.5 kV/cm，提高了3%，说明水珠数量增多加剧了模型的电场畸变程度。分析这一现象的原因，水作为极性电介质，在外界电场的影响下产生等效束缚电荷，增强了水珠、空气和硅橡胶三交界点处的电场。

3 试验结果

3.1 水珠电导率的影响

本文采用不同NaCl添加量水溶液模拟绝缘子上不同污秽程度的情况。模型的起晕和闪络电压试验结果如图8所示。

图8 电导率对起晕电压和闪络电压的影响Fig. 8 The influence of conductivity on corona inception voltage and flashover voltage

从图8中可以看出，水珠电导率为1.97 μS/cm和1 326 μS/cm时，样片的起晕电压从21.1 kV变为24.1 kV提高了14%，这与图5(a)中的仿真分析结果一致，起晕电压提高原因是，当施加电压较低时，绝缘子所处的电场可等效为静电场，水珠电导率提高降低了其介电常数，在外加电压一定时，降低了电场畸变，提高了模型起晕电压。

而当水珠电导率为1.97 μS/cm和1 326 μS/cm时，闪络电压则由27.4 kV变为25.2 kV,下降了8.4%，这与这与图5(b)中的仿真分析结果一致。闪络电压下降的原因为随着施加电压至即将闪络，泄漏电流不可忽略，在电流场中，随着水珠电导率的提高，流过绝缘通道的泄漏电流增大，泄漏电流的热效应容易导致干带的产生，提高增强了电场的畸变程度，导致闪络电压降低。

3.2 水珠模式对起晕位置的影响

采用日盲型紫外成像仪分别研究了伞裙和芯棒模型下水珠的放电位置，水珠电导率为1.97μS/cm，体积为0.18 mL。实验结果如图9所示。

图9 电极形式对起晕位置的影响Fig. 9 Influence of electrode model on corona

图9(a)为伞裙模型，随着电压的升高，水珠顶端出现放电光斑。图9(b)为芯棒模型电晕放电光斑，放电位置集中于水珠、空气和硅橡胶三者交叉点附近。实验结果与图6分析结果一致。

由试验得到模型对放电的影响如表3所示。

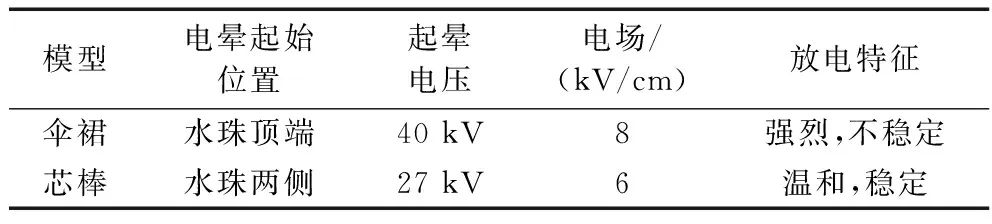
表3 模型类型对放电特性的影响

由表3和图9(a)可知，伞裙模式下放电位于水珠顶端，起晕电压平均值为40 kV，平均电场强度为8 kV/cm，放电产生和紫外放电光斑的噪声均较大，放电较为剧烈，但不稳定，期间会有短暂的熄灭过程。放电不稳定的原因是，放电开始后，水珠受电动力拉伸向四周延展而减弱电场，放电熄灭，达到新的稳状态后放电持续，但熄灭现象随着电压进一步提高而消失。

由表3和图9(b)可知，芯棒模式下放电位于水珠两侧，起晕电压平均值为27 kV，放电平均电场值为68 kV/cm，放电声音和紫外光斑变化较为温和，放电相对稳定。两种模型下均在大约45 kV被击穿。