改进GA-BP 神经网络在盾构推进地面沉降中的预测及应用
2021-12-17王雪明刘陕南肖晓春包蓁
王雪明,刘陕南,肖晓春,包蓁
(1 上海工程技术大学 城市轨道交通学院,上海 201620;2 上海隧道工程有限公司,上海 200032)
0 引言
在传统城市隧道施工引起地面变形的预测方法中,有Peck 公式法、有限单元法等[1]。与此不同,神经网络方法因其强大的数据计算处理能力逐渐得到应用。本文依托北横通道新建工程,工程利用一台直径为15.56m 的泥水气压平衡盾构机下穿城市密集建筑区掘进隧道。对于盾构推进引起的地面变形,通过神经网络的方法进行预测研究。
孙钧等通过整理实测资料并对土体扰动机理进行分析,说明根据监测资料并利用神经网络可以对盾构隧道施工过程中的地层移动进行有效的动态实时预测[1];李红霞等利用遗传算法优化BP 神经网络的初始权重,建立模型对地下水位影响强度进行分析,说明地面沉降与地下水位存在一致响应趋势[2];王志亮等将杂交法与改进BP 法、多元回归法对比,预测粉喷桩的抗压强度,即先用遗传算法对全局进行训练,再用BP 网络进行精度训练,加快了网络的收敛,避免了局部极小问题的出现,达到了要求的预测精度[3];王睿等结合实际工程,通过将传统的BP 神经网络与遗传算法相结合的方法,实现针对实际隧道工程施工参数与隧道变形值之间的正反演分析,达到了高效且相对准确的沉降预测及支护参数的最优寻找[4]。
综合以往研究分析发现,神经网络方法及其一系列优化方法在预测盾构推进施工引起地面变形中的应用成果斐然,但在面对具体工程数据时神经网络凸显的自身缺陷问题还有待研究。
本文拟采用软件编程数据处理的方法,以BP神经网络为研究点,利用遗传算法优化模型训练所需的初始权重,并基于实测数据的特点,改进遗传算法的种群遗传规则,探究BP 神经网络局部最优问题。
1 计算原理
1.1 BP 神经网络误差反向传播原理
BP 神经网络,即Back-propagation Neural Network,采用权值阈值正向传播计算,反向修正的方法对数据进行训练拟合[5],即构建的网络模型随机初始化给出各层的连接权值和阈值,对网络输入层每组数据各个维度上的数值进行连接权、阈值的计算,传播到隐含层并通过该层神经元上的传递函数计算各单元的输出,再对此输出进行连接权、阈值的计算,传播到输出层,通过该层神经元上的传递函数计算网络的最终输出值,将网络实际输出与目标输出进行误差计算,当误差值不满足预设条件时,反向修正各层连接权值、阈值,往复迭代直到满足网络预设条件之一,完成网络训练。其中,隐含层传递函数一般为S 型函数,输出层一般为purelin函数,即线性函数[6]。计算原理如图1 所示。
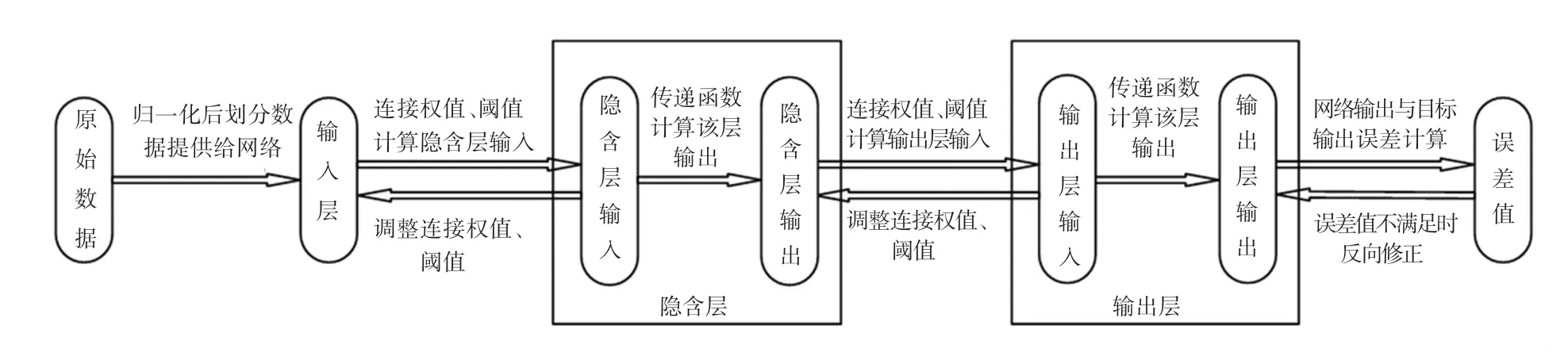
图1 BP 神经网络算法数据训练原理Fig.1 The principle of BP neural network algorithm data training
1.2 遗传算法(GA)优化的BP 神经网络
传统BP 神经网络有一些难以克服的局限性,如局部最优问题、初始权重敏感性、网络不可重现性等等[5,7]。很多学者因此引入遗传算法,用以克服BP 的缺陷。
遗传算法,即Genetic Algorithm,是一种学习生物界自然选择和自然遗传机制构建的随机优化搜索算法[4,8]。算法在目标函数的基础上计算适应度值,依据适应度值进行遗传操作,寻优规则由概率决定,更容易将较优个体遗传至下一代,其与BP 神经网络的结合是优化的重点,也是编写程序的前提。
一方面,遗传算法中要针对优化对象定义个体适应度值。基于遗传算法的原理,先将训练均方误差值FY 作为目标函数,即拟合值与真实值之差的平方和的平均值,公式(1)表示:
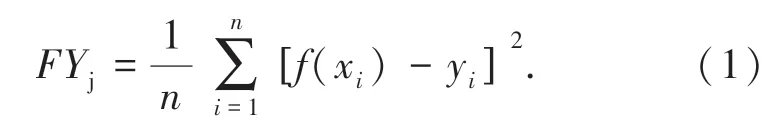
再对其计算适应度值,以此衡量个体对于种群的适应程度,用公式(2)表示:

当目标函数FY越小,适应度值FF越大,表明此时的个体更适应会被遗传到下一代。
另一方面,为了结合遗传算法,先对BP 循环训练n次,并将这n次随机生成的初始权值阈值通过矩阵转换后,再利用实数编码,可以形成初始种群,初始种群即包含n组遗传个体[9-10]。
结合以上两方面,在个体适应度的基础上计算个体概率和累计概率,分别如公式(3)、(4)所示:
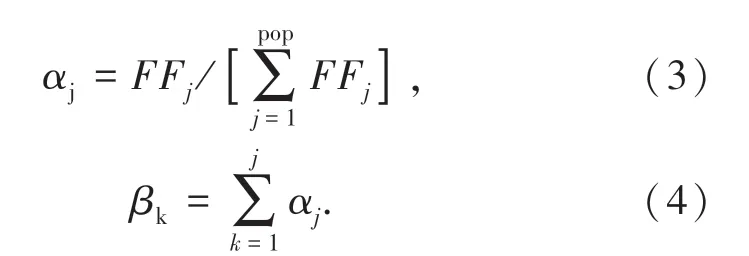
适应度值越高的父本个体,越容易被选中,即按照选择概率随机数执行选择操作,之后再进行交叉操作、变异操作。这样得到新的n组个体,即构成第二代种群,再对其进行实数解码,转换为权值阈值矩阵回赋网络训练,计算新个体的均方误差、适应度值。
由此,可将遗传算法基本步骤描述如下[4]:
(1)确定编解码方案,生成初代种群;
(2)根据目标函数计算个体适应度;
(3)选择操作;
(4)交叉操作;
(5)变异操作;
(6)新一代种群,及其适应度值计算;
(7)返回(3),直至达到预设遗传代数或满足误差要求。
经过遗传算法的优化操作后,网络再训练所需的初始权重不再是随机给出,而是建立在遗传操作上的收敛优化,从而得到较稳定的训练结果。
1.3 改进的GA-BP 神经网络
传统遗传算法由于随机数的依赖性,在个体的选择操作上存在很多可能性,即并不一定是最优个体被选中或多次选中。
为了能达到更优化的训练效果以及提高训练的时效性,应该对算法中的种群遗传规则进行改进,即从各代种群中人为保留较优的个体。为了使保留的优化个体构成的新初代种群与最初种群规模一致,在程序的编写上应该针对初始种群包含的全部个体数先期进行成倍的遗传代数操作。
如以10 组个体生成初始种群,先对初始种群进行10n代数的遗传操作,产生全部的10n组、每组10 个数量的均方误差数据集,可对应从中摘取匹配初始种群个数数量的最优个体,于是摘取的优化个体构成新的初代种群,再以新初代种群进行10n代数的遗传操作。以此往复,定义这样的优化方法的每次循环操作为“优化次数”,整合程序完成训练,直到优化次数满足预设数量或误差值满足条件,优化完成。具体流程如图2 所示。
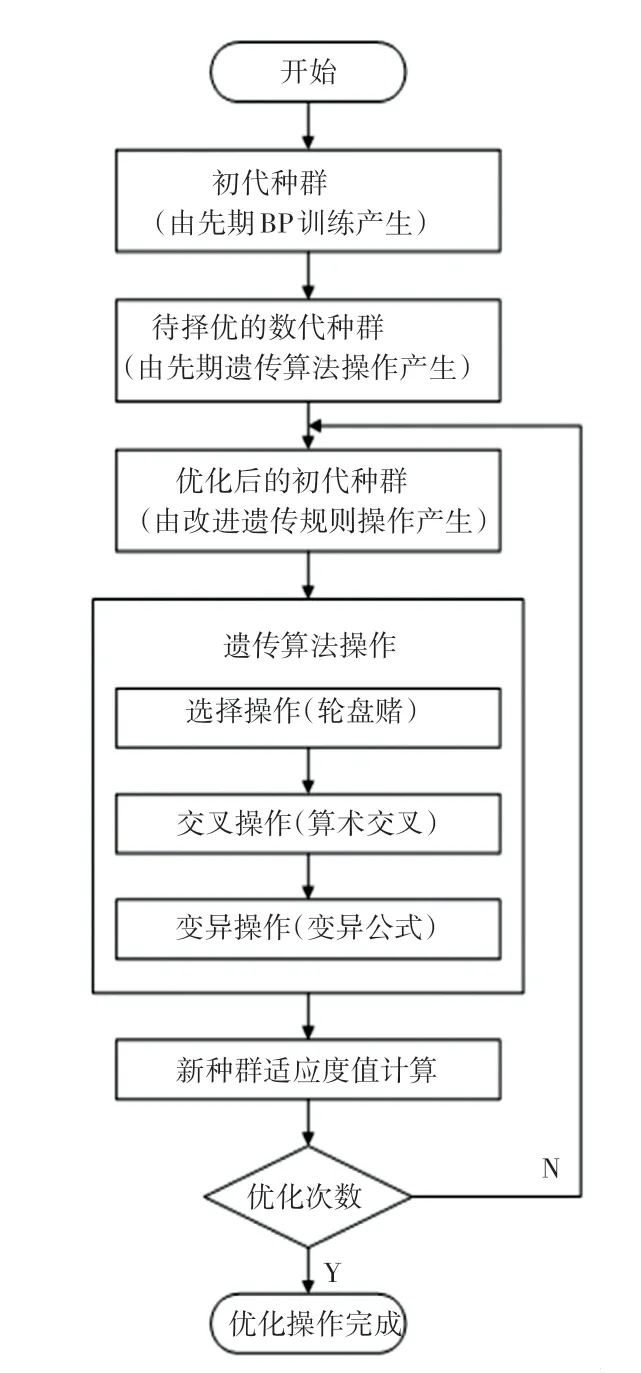
图2 改进的遗传算法计算原理思路Fig.2 The principle of improved genetic algorithm
2 工程概况与模型的建立训练
2.1 工程概况与原始数据整理
本文背景工程为上海北横通道新建工程Ⅱ标,项目主要施工内容为主线盾构隧道段,所用泥水气压平衡盾构机直径达到15.56 m,即定义为超大直径泥水盾构隧道,沿线地质复杂,隧道穿越土层以粉质黏土为主,隧道下方已进入砂性土地层,总体地层分布为典型的黏土、砂土复合断面,如图3 所示,土层物理力学性能见表1。在盾构区段覆土上方地面存在较多如住宅楼,商场等建构筑物,若盾构施工参数控制不当,极易造成盾构失稳,引发地面变形,影响地面以上建构筑物的使用。
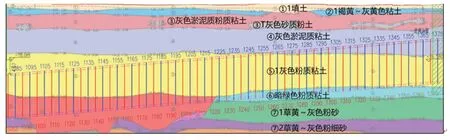
图3 北横隧道部分区段地层分布示意图Fig.3 Distribution of strata in some sections of North Cross Tunnel
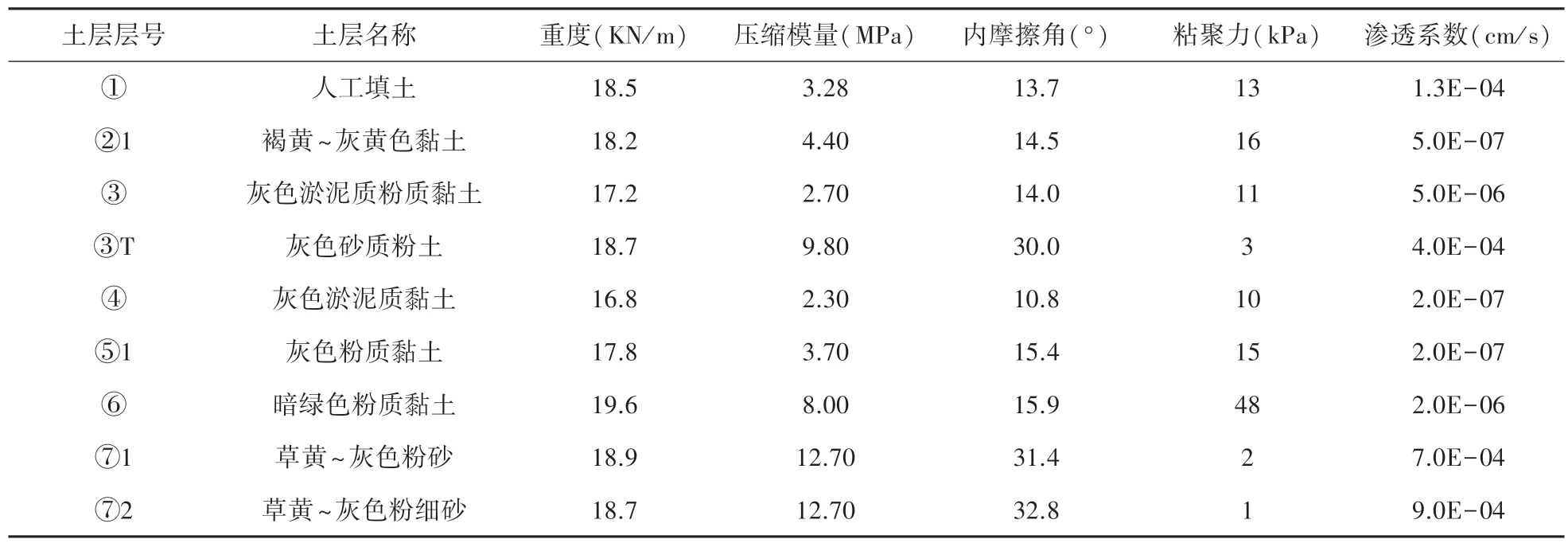
表1 土层物理力学性能参数表Tab.1 Table of physical and mechanical properties parameters of soil layer
盾构推进引起的地面变形是一个复杂的非线性问题,在盾构推进过程中不断发展变化,其中切口面上方地面变形和注浆引起的地面变形尤为突出。本文聚焦于神经网络方法研究,主要针对盾构切口面上方地面变形进行分析,也即将盾构切口面上方地面变形作为BP 神经网络数据拟合及预测对象,参考相关研究成果,对采集的盾构段原始数据经过整理筛选后,选定6 个参数作为BP 神经网络输入端的处理对象,具体为隧道开挖面上方覆土厚度、盾构开挖推进速度、盾构总推力;盾构开挖截面土体压缩模量、内摩擦角、粘聚力见表2。

表2 神经网络模型输入输出数据Tab.2 Input and output data of neural network model
2.2 神经网络模型的建立
本文通过MATLAB 软件构建网络实操程序算法。按照原理流程,前一部分模型的建立包括:
(1)原始数据归一化、数据划分。即对整理的40 组现场实测数据依据数据归一化原理变换成[-1,1]之间的数值[10],再将1~30 组划分为训练样本,31~40 组为预测样本;
(2)BP 网络参数预设和模型的建立。基于表2的工程实测数据可知,输入端变量维数为6,输出端维数为1,根据隐含层节点数计算经验公式(5)[5]:
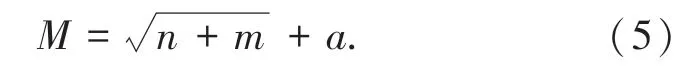
其中,n和m分别为输入、输出层的神经元个数,依据上文分别为6 和1,a是[0,10]之间的常数,且为了避免隐含层节点数设置较多时会导致训练时间过长或过拟合的缺陷,取隐含层神经元数为M=4,即构成6-4-1 的BP神经网络模型。
模型建立完成后,利用MATLAB 继续编写代码实现各方法的具体实操,即:
(1)构建循环节形成BP 方法。在循环节中随机生成网络训练所需的权值阈值,并将其作为网络训练的初始权重回赋给已建立的网络模型,随即进行网络的训练、预测及相关数据的输出。
(2)融合遗传算法构成GA-BP 方法。先将BP训练10 次中随机给出的网络初始权重作为遗传算法的初始化种群,再将经选择、交叉、变异后的种群回赋给网络计算适应度值,以此构建循环节往复进行1 000代的遗传操作,直至遗传代数达到预设值为止。
(3)对遗传算法的种群遗传机制进行改进,形成改进的GA-BP 方法。先将BP 训练10 次中随机给出的网络初始权重作为遗传算法的初始化种群,再利用遗传算法进行10 代的遗传操作,并人为从10 代遗传操作中选出每代最优个体作为下次10 代遗传操作的新初始种群,将最优个体的不断选择定义为“优化次数”,循环直至达到预设值1 000为止。
2.3 训练结果输出与分析
对于BP 方法,为了避免局部最优,采用多次随机训练的方式,寻找最优结果,故设置循环次数为1 000,依据构建的循环节,网络每次随机给出[-1,1]之间不同的初始权重,执行程序完成训练操作,在这1 000次训练中找到相对较优结果。
对于GA-BP 方法和改进的GA-BP 方法,分别完成1 000代遗传操作和1 000次优化操作,保留各方法实操结果,整理网络计算数据,绘制训练样本均方误差变化曲线和各方法最优网络输出拟合曲线,如图4~5 所示。

图4 三方法训练均方误差变化曲线Fig.4 Three-method training mean square error variation curve
由图4 可以看出,BP 方法整体训练均方误差值较大且出现个别几次误差值异常大的情况;而相比之下GA-BP 方法均方误差值有了很大幅度的降低,不再有异常大误差值的出现,均方误差整体保持在一个较小的范围内;相比前两项操作,改进的GA-BP 方法均方误差值表现出更好的降低趋势。
重复对3 个方法的实操发现,由于BP 方法每次给出的初始权重不同,故训练结果依然表现出离散性大的缺陷;而利用遗传算法对BP 网络训练的初始权重进行优化后的GA-BP 方法,训练结果显示均方误差均可以保持在一个较小的区间范围;再到改进的GA-BP 方法,均方误差降低趋势的出现也不是偶然的,任意给出一组初始权重,经过网络实操后均可得到如图4(c)所示的误差降低曲线,训练结果不再依赖网络限定的最初权重,这对最优训练效果的寻找具有积极意义。
结合图5 的网络输出拟合曲线可见,BP 方法最优的一次训练结果拟合表现良好,即可以说明BP方法实现的大量随机训练避免了一次训练可能会出现的局部最优现象,从而得到较好的拟合效果;3 种方法拟合曲线对比,不难看出,改进的GA-BP 方法拟合效果较前两个方法整体更接近实测值。
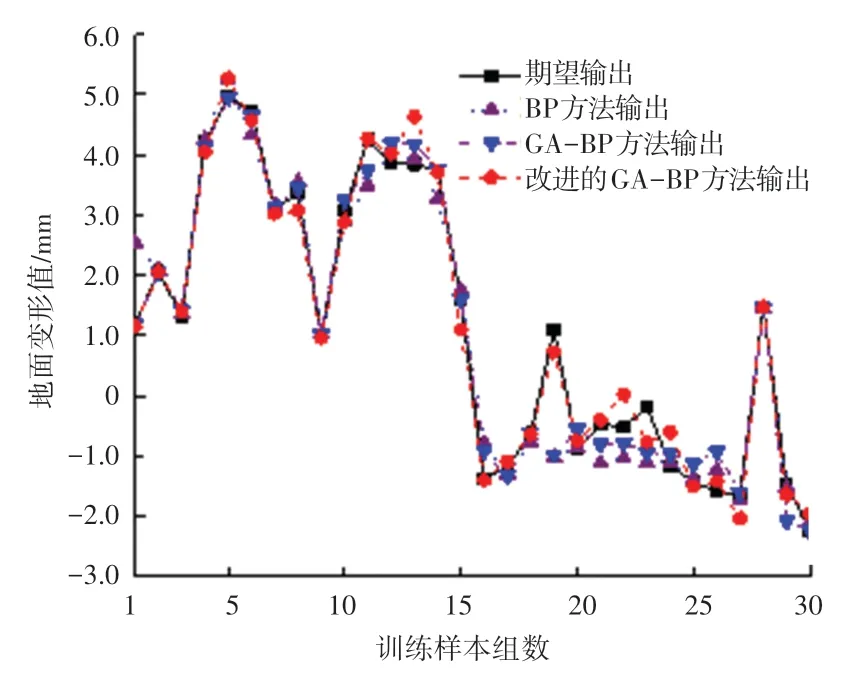
图5 3 种方法训练拟合曲线Fig.5 Three-method training fitting curve
为了探究各方法网络训练后的预测能力,在网络训练完成后也进行了预测实操,并绘制预测样本的网络输出拟合曲线,如图6 所示,可见3 种方法最优训练输出对应的预测效果也是较满意的,改进的GA-BP 方法较前两种方法预测值整体更贴近实际地表变形值。
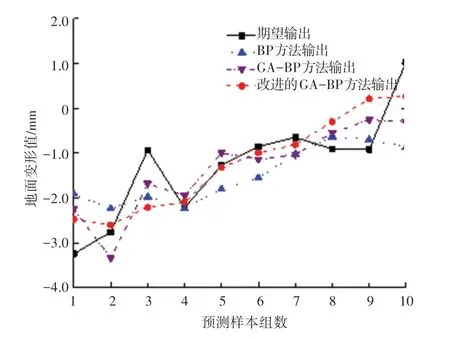
图6 3 种方法预测拟合曲线Fig.6 Three-method predicting fitting curves
不妨从定量化的角度,对比3 种方法的训练和预测精度,见表3。对比BP 方法,遗传算法优化的BP 神经网络提高了训练稳定性;再将改进的GABP 方法和前两种方法对比,可见其误差值得到有效的降低,如改进的GA-BP 方法较前两种方法训练误差降低了50%以上,预测误差降低了25%以上,各项误差最小、预测精度达到最高。

表3 3 种方法定量分析Tab.3 Quantitative analysis of three methods
2.4 优化方法预测能力检验
为了进一步测试改进的GA-BP 方法对盾构推进引起地面变形的预测能力,整理出100 组实测数据,将前90 组作为训练样本,后10 组作为预测样本,执行程序,经过1 000次优化操作后,绘制出预测均方误差变化曲线如图7 所示,可见在优化次数为0~100的区间内,误差迅速下降,从而保证预测拟合结果快速的稳定在一个可以接受的精确度,提高了预测工作效率,并且随着优化次数的继续增加,误差可以继续下降收敛至更低值,但下降的速度有所减缓。
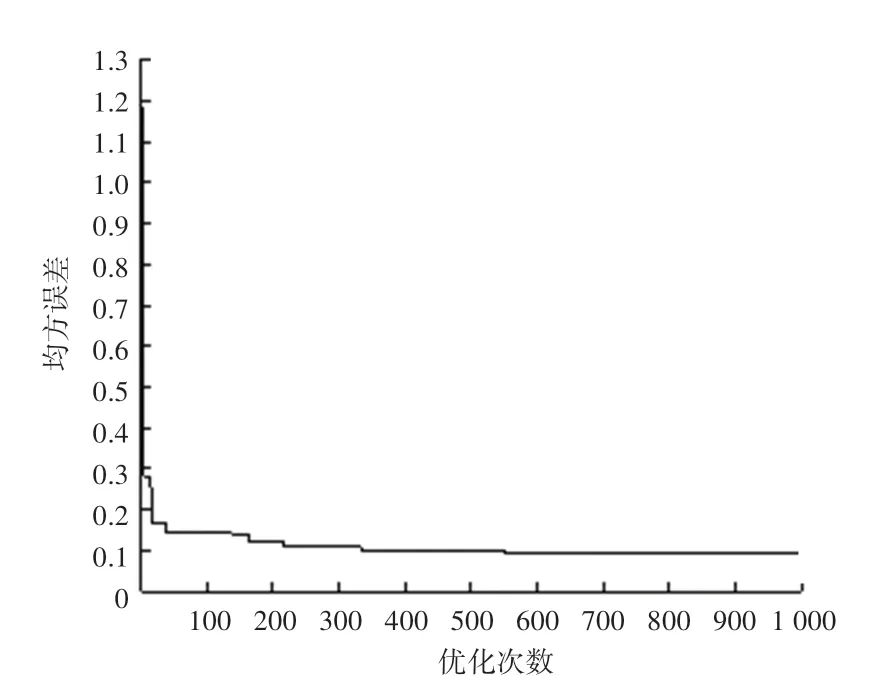
图7 改进的GA-BP 方法预测均方误差变化曲线Fig.7 Improved GA-BP method predicting mean square error variation curve
对比优化次数为100、300、1 000时的预测拟合曲线,如图8 所示,可见网络经过100 次的优化操作时,该方法的预测值趋势与实测值总体吻合,当优化次数达到1 000时,预测值最接近实测值,预测达到了更高的精度。
如图8 所示,对比100、300、1 000 次的预测误差值,整理输出数据见表4,可见:

图8 改进的GA-BP 方法预测拟合曲线Fig.8 Improved GA-BP method predicting fitting curve
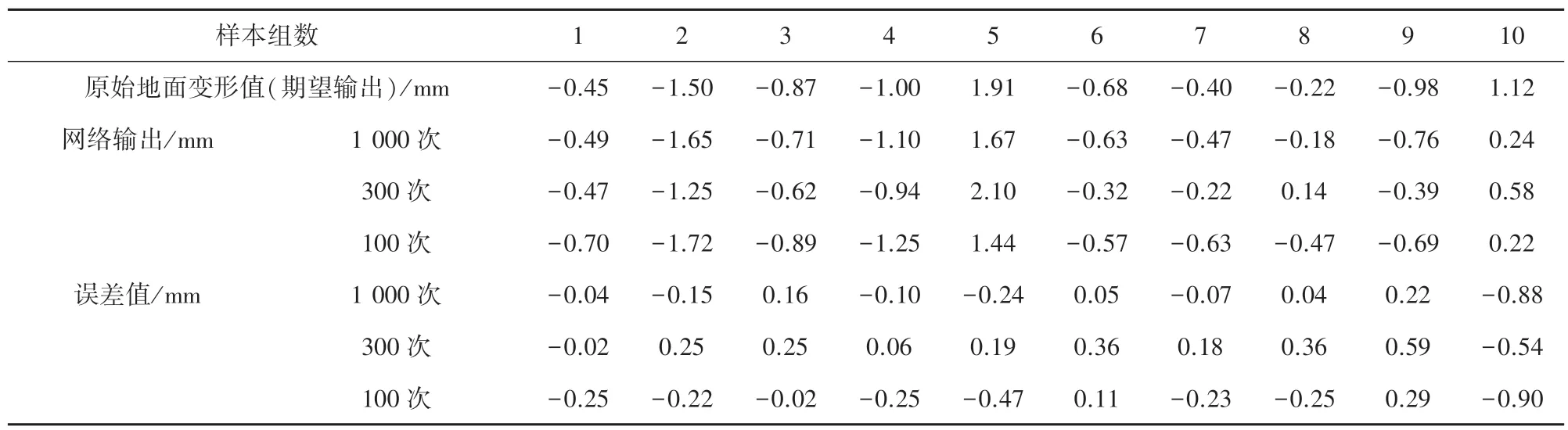
表4 预测精确度计算分析Tab.4 Analysis of predictive accuracy
(1)一般情况下,采用改进的GA-BP 方法预测盾构推进引起的地面变形时,网络经过100~300 次优化操作后,即可将大部分样本误差控制在10%~25%之间;
(2)若想继续提高预测精度,可根据实际需求继续增大优化次数,从而得到更理想的预测效果,使得预测值更接近实测值;
(3)对于部分样本组误差较大的情况,考虑到算法、输入变量等还有值得改进的地方,这将在后续的研究中继续深入,进一步提高预测精度。
3 结束语
(1)BP 神经网络在数据预测上具有较好且较便捷、省时的研究价值。但传统BP 存在训练误差离散性大的缺陷,即初始权重敏感性大导致网络训练不稳定;
(2)利用遗传算法对BP 神经网络的初始权函数进行优化后,大大减小了传统BP 神经网络的训练随机性和离散性,避免了极大误差值即极差训练结果的出现,说明优化初始权函数对提高BP 神经网络的训练稳定性和拟合精度有较好作用;
(3)对GA-BP 中的种群遗传规则进行改进后形成的改进GA-BP 方法很好的完成了网络训练的优化,训练和预测结果都达到了更高的精度,通过新数据的预测也进一步验证了此方法在盾构隧道引起地面沉降预测中应用的可推广价值;
(4)本文着重进行了神经网络方法的比较与优化研究,因此以地面沉降作为输出,参考了类似研究成果选取了影响盾构上方地面沉降的6 个参数作为输入端变量,经过实测数据分析能对地表沉降进行有效预测。后续还可以进一步深入研究,譬如加入注浆参数用以研究注浆和盾尾脱出后的地表沉降预测问题。
