基于结构图像先验与ASM 能量的服装图像去噪

赵长乐，何利力

（浙江理工大学 信息学院，杭州 310018）

0 引言

服装图像［1］在采集的过程中，受环境、设备、人为因素的影响不可避免地会引入噪声，导致图像质量降低，从而影响人眼的观感，对服装图像进一步地处理也会受到一定影响。图像去噪［2］希望使用图像自身的信息来去除图像噪声，同时不影响图像本身的细节，以获取与原始图像更加接近的去噪图像。由于服装图像纹理的复杂性和多样性，对其进行去噪时需要更加注重细节的完整性，因此有必要对服装图像进行高质量的去噪处理。

空间域图像去噪算法［3］对图像中每个像素点的灰度值加以处理，以滤波的方式进行；均值滤波使用线性平滑技术，用邻域窗口中全体像素的平均值代替原有的像素值；中值滤波使用非线性平滑技术，将每一像素点的值设置为该点邻域窗口内的所有像素点的中值；高斯滤波则根据邻域间像素距离大小的高斯加权来分配权重，以邻域像素值的加权和代替原有像素值。

变换域图像去噪算法将图像经过某种变换由空间域转换到变换域，在变换域内根据噪声分布特征，设定相应的抑制模型对噪声进行消除，然后通过逆变换复原图像。代表性的方法有小波变换［4］、复小波变换［5］、轮廓波变换［6］等。虽然此类算法能够较好地去除图像噪声，且对图像信息损伤较低，但不能很好地对纹理和噪声进行区分，导致图像出现阶梯效应。

现阶段有很多将空间域去噪和变换域去噪相结合的算法。如，袁明月等［7］将中值滤波算法与小波变换相结合，利用高斯噪声来模拟图像中含有的噪声，通过对经过中值滤波预处理后的图像进行二级小波变换，对于高频子带，通过逐点计算灰色关联度，并将其与经典小波阈值进行对比，来实现各高频子带的滤波，通过小波逆变换得到去噪后的图像。深度学习在图像去噪领域同样也取得了良好的进展。李传朋等［8］使用卷积子网和反卷积子网构建了一种对称式网络结构，将噪声图像作为神经网络的输入，原始图像作为输出，经过数据集的训练，使得卷积子网学习图像特征，反卷积子网可根据学习到的特征恢复原始图像，并结合修正线性单元获取更多的纹理细节。基于CNN 的图像去噪技术使用手工构造的噪声图像数据集进行训练，在加性高斯白噪声图像上表现突出，但在真实噪声图像上表现不佳。

本文结合图像灰度共生矩阵［9］中的ASM 能量，通过深度学习方法对图像进行降噪。根据Ulyanov等［10］所提出的思想，图像的先验特征可以由网络结构表示（结构图像先验），而非网络中的参数（参数图像先验）。对于一个图像生成的卷积神经网络，以随机向量作为输入，完整图像作为目标输出，通过对网络进行训练，可生成目标输出图像。目标图像的ASM能量越低，生成所需要的迭代次数越多，对于同样的网络结构，要生成噪声图像比生成自然图像需要更多的迭代次数。根据这一特性，将噪声服装图像作为目标输出，在网络迭代至ASM能量极大值处停止训练，此时的网络输出即为去噪后的服装图像。

1 灰度共生矩阵与图像ASM 能量

灰度共生矩阵是1973 年由Haralick等人提出的一种通过研究图像灰度的空间相关特性，来描述图像纹理的常用方法。由于纹理是由灰度分布在空间位置上反复出现而形成的，因而在图像空间中相隔某距离的2 像素之间会存在一定的灰度关系，即图像中灰度的空间相关特性。

灰度直方图是对图像上单个像素具有某个灰度进行统计的结果，而灰度共生矩阵是对图像上保持某距离的2 像素分别具有某灰度的状况进行统计得到的。例如：取大小为N×N的图像中任意一点（x，y）及偏离其的另一点（x＋a，y＋b），设该点对的灰度值为（g1，g2）。令点（x，y）在整个画面上移动，则会得到各种（g1，g2）值；设灰度值的级数为k，则（g1，g2）的组合共有k2种。对于整个画面，统计出每一种（g1，g2）值出现的次数，并将这些值排列成一个k × k的方阵P（g1，g2），再对该方阵进行归一化，最终得到的k × k大小的方阵称为灰度共生矩阵，记作G（g1，g2）。距离差分值（a，b）取不同的数值组合，可以得到不同情况下的联合概率矩阵，取值要根据纹理周期分布的特性来选择，对于较细的纹理，选取小的差分值。由于服装图像的纹理较为精细，因此本文选取（1，0）作为差分值，此时像素对是水平的，即0 度扫描。这样，两个像素灰度级同时发生的概率，就将（x，y）的空间坐标转化为“灰度对”（g1，g2）的描述，然后对计算得到的概率进行如下归一化，就得到了灰度共生矩阵。

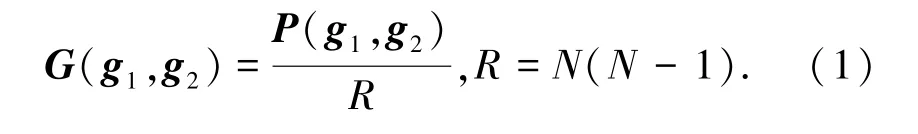
从直觉上来说，如果图像是由具有相似灰度值的像素块构成，则灰度共生矩阵的对角元素会有比较大的值；如果图像像素灰度值在局部有变化，那么偏离对角线的元素会有比较大的值。于是产生了一些由灰度共生矩阵所衍生出的标量，用以表征灰度共生矩阵的特征，ASM 能量作为这些标量中的一种，通过灰度共生矩阵中每个矩阵元素的平方和来表示：

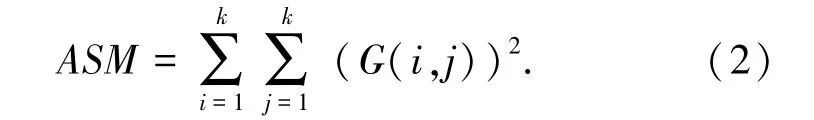
若灰度共生矩阵中的值集中在某一块（如接近纯色的图像），则ASM有较大值；若G中的值分布较均匀（如噪声严重的图像），则ASM有较小的值。通过ASM值的大小可以反映图像灰度分布的均匀程度和纹理的粗细程度。

2 结构图像先验与图像去噪方法

2.1 结构图像先验理论

通常的深度学习理论认为，图像的先验分布从大量的数据集中获得，图像生成网络从数据集中训练得到的网络参数代表图像的先验信息。但是，将一切信息来源归结于对数据集的训练可能产生灾难性的后果。如，Zhang等人［11］所述，在图像分类任务中，若对图像进行随机标注，训练集同样可以拟合得很好，但是训练集以外的图像网络则无法识别；Dario等［12］所述，对于在训练集中未出现的特征，网络无法正确识别；Ulyanov等［10］认为，图像的先验信息可以由网络结构所表征，并不需要通过训练从大量的数据集获得先验信息。对于图像生成问题，可以直接将未训练的网络作用于图像。若网络足够优越，图像的所有纹理、结构等细节特征都能被网络结构表示，网络的参数仅仅决定这些特征的强弱。

一个图像生成网络可以用函数x＝fθ（z）表示，该函数将向量z映射到图像x。其中，θ代表网络中需要学习的参数，映射f可视为网络结构，可包含如卷积、池化、非线性激活等一系列操作，该方法可以从随机分布中生成真实图像。对于图像生成问题，初始并不知道所要生成的图像本身，需要通过已知的、有缺陷的图像x0，使函数得到x满足真实图像的分布。图像生成任务可以用公式表示为：

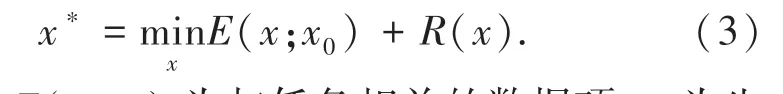
其中，E（x；x0）为与任务相关的数据项；x为生成图像；x0为有缺陷的图像；R（x）为正则项。对于以参数图像先验为理论基础的图像生成任务，正则项的选择是一个难点，通常表示数据集中图像的方差。而对于以结构图像先验为理论基础的图像生成任务，由于没有用于训练的数据集，所以可将正则项隐含在网络结构中，公式可转化为：

此时，对于所有网络能生成的图像R（x）＝0，对于其它不能生成的图像R（x）＝∞。

对于一个足够好的网络结构而言，若将其作为图像的先验特征应可以拟合所有的图像，包括随机噪声所形成的图像，此时的网络结构对生成的图像不作任何限制。尽管理论上可以从网络中生成任意的图像，但是图像的类型决定了该图像的生成速度。图2 显示了将纯色图像、自然服装图像、含噪声的服装图像、高斯噪声图像分别作为目标生成图像时，网络的迭代次数与MSE 之间的关系；图1 显示了这4幅图像的示意图，以及各图像对应的ASM 能量值。由此可以看到，ASM 能量值越高的图像，使用相同网络生成，所需要的迭代次数越少。

图1 不同图像对应的ASM 能量值Fig.1 The ASM energy values corresponding to different images

图2 不同目标图像的迭代曲线Fig.2 Iteration curves of different target images

2.2 图像去噪方法

为了将结构图像先验理论应用于图像去噪，设定图像去噪的数据项为：

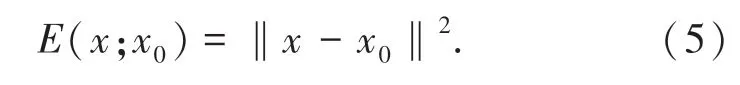
式中，x0表示含噪声的图像，x表示网络生成的图像。此时，图像去噪的目标函数转化为：

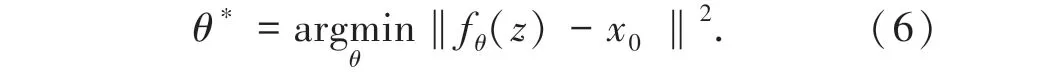
以含噪声的图像作为目标输出，希望能在网络训练的过程中找到合适的参数θ*，使得网络输出去噪后的图像。图5 截取了以含噪声的服装图像作为目标输出进行训练，迭代次数处于100、500、1 000、4 000、10 000时所生成的图像。可以看到，生成的图像由最开始的混乱噪声，到含有部分特征的图像，再到自然图像，最后生成被噪声污染的图像。图3 显示了使用含噪声服装图像为目标图像进行训练时，所生成图像与自然服装图像的峰值信噪比（PSNR）随迭代次数的变化曲线，图4 显示了生成图像的ASM 能量与迭代次数的关系曲线。所生成图像的ASM 能量值先增大后减小，在迭代次数为4 000附近，ASM 能量处于极大值，两者的PSNR 同样在迭代次数4 000时处于极大值附近，此时对应的生成图像最接近自然服装图像。

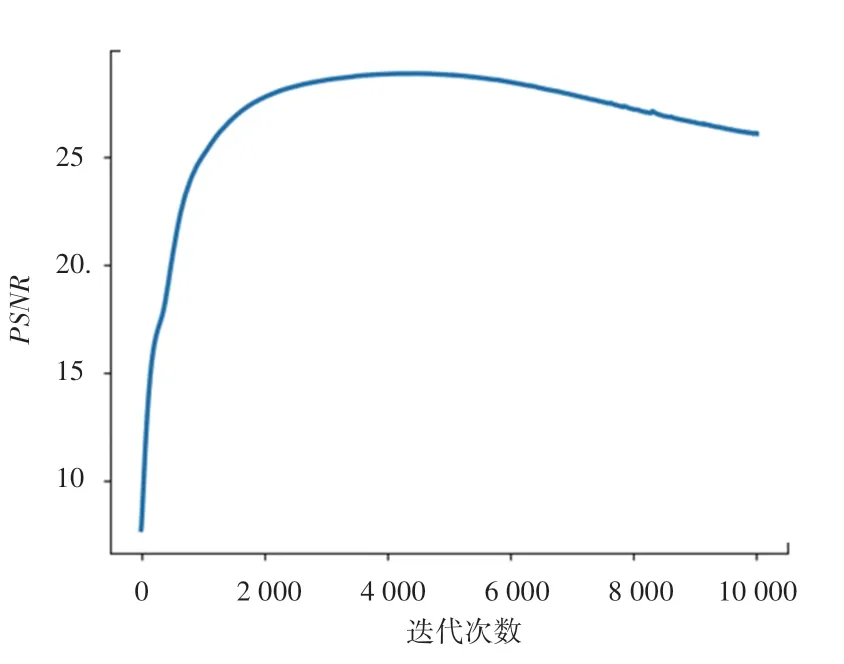
图3 PSNR 与迭代次数关系曲线Fig.3 Relation curve between PSNR and iteration number

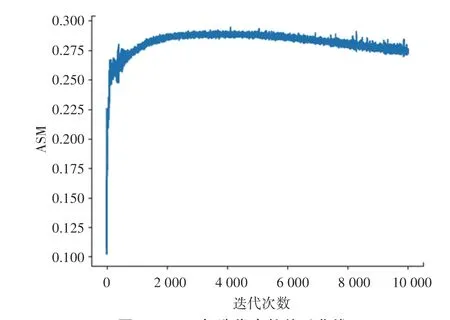
图4 ASM 与迭代次数关系曲线Fig.4 Relation curve between ASM and iteration number

图5 不同迭代次数对应的生成图像Fig.5 Generated images corresponding to different iterations

实验结果表明，在图像生成网络训练的过程中，图像中的低频特征会先于高频特征拟合。以含噪声图像为目标图像进行训练时，图像中的噪声属于高频特征，在迭代后期才会出现。对应到ASM能量而言，网络在迭代的过程中会先生成一个ASM能量值较高的图像，该图像与自然服装图像相近，随着迭代过程的继续进行，生成图像的ASM能量值会缓慢降低。如果对一个图像生成网络能找到合适的迭代次数，就能生成一幅去噪效果良好的图像。图3 曲线中PSNR的极大值点与图4 曲线中ASM的极大值点对应的迭代次数接近。在训练过程中当ASM能量处于极大值时对迭代进行截断，取此时的生成图像为去噪图像。

3 实验结果

3.1 实验数据与网络结构

为验证本文算法的优良性能，从网上选择不同类型的9 张服装图像进行实验。所有图像均裁剪至512×512 大小，如图6（a）所示。实验选用了被高斯噪声污染的原始图像作为要修复的目标图像。对原始服装图像添加噪声强度σ＝25 的高斯噪声后，图像的局部如图6（b）所示。

图6 实验使用服装图像示意图Fig.6 Schematic diagram of clothing used in experiment

实验使用UNet 网络结构，包含可训练参数的网络层共有10 层。网络中，下采样通过步长为2 的跨步卷积实现，每次下采样特征图尺寸减小为之前的一半，上采样通过最邻近差值算法实现，每次上采样特征图尺寸增加一倍。所有的卷积核均使用3×3大小。网络示意如图7 所示。

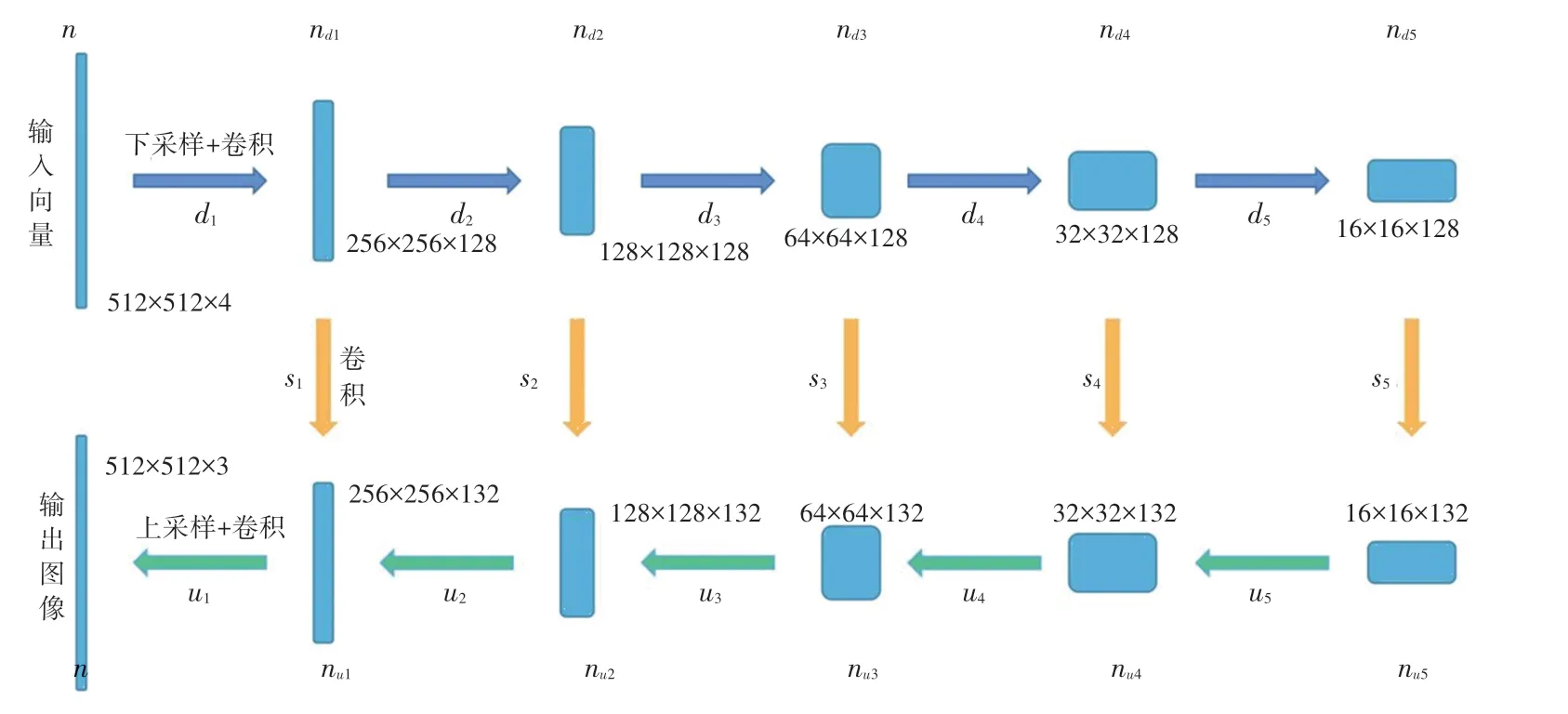
图7 网络结构示意图Fig.7 Schematic diagram of network structure

实验选用大小为512×512×4，方差σ＝0.1 的高斯噪声作为网络的输入，输出大小为512×512×3 的图像，噪声服装图像与输出图像的MSE作为网络的损失函数。网络选用Adam 优化算法，学习率固定为0.01。算法设定的停止条件为：当前100 次迭代的平均ASM 能量小于前100 次迭代的平均ASM 能量时，停止迭代。对生成的图像使用指数滑动平均提升去噪效果，指数滑动平均的权重参数选用0.99，共使用2 次指数滑动平均对输出图像进行优化。

基于本文算法的所有实验均在Colab 平台上进行，实验使用的GPU为K80，深度学习框架选用pytorch。

3.2 实验结果分析

为了验证本文去噪算法的有效性，将图7 中的服装图像分别使用guided、NL－means（NLM）、CBM3D 与本文提出的去噪算法进行比较，使用PSNR衡量各算法的去噪效果。各算法对9 张测试图像进行去噪的结果见表1，去噪后图像的局部特征对比如图8 所示。

图8 不同算法去噪效果图Fig.8 Denoising effect diagram of different algorithms

从表1 的结果中可以看到，本文方法相比guided 和NLM 算法去噪效果更好，略差于CMB3D算法。但CMB3D 算法为非盲去噪，需要估计图片中噪声的强度，若估计出的噪声强度与实际噪声强度有偏差，则非盲去噪效果会受到较大影响。本文方法为盲去噪，对任意噪声强度均采用统一去噪算法，真实图片的噪声分布未知，盲去噪算法更具有一般性。

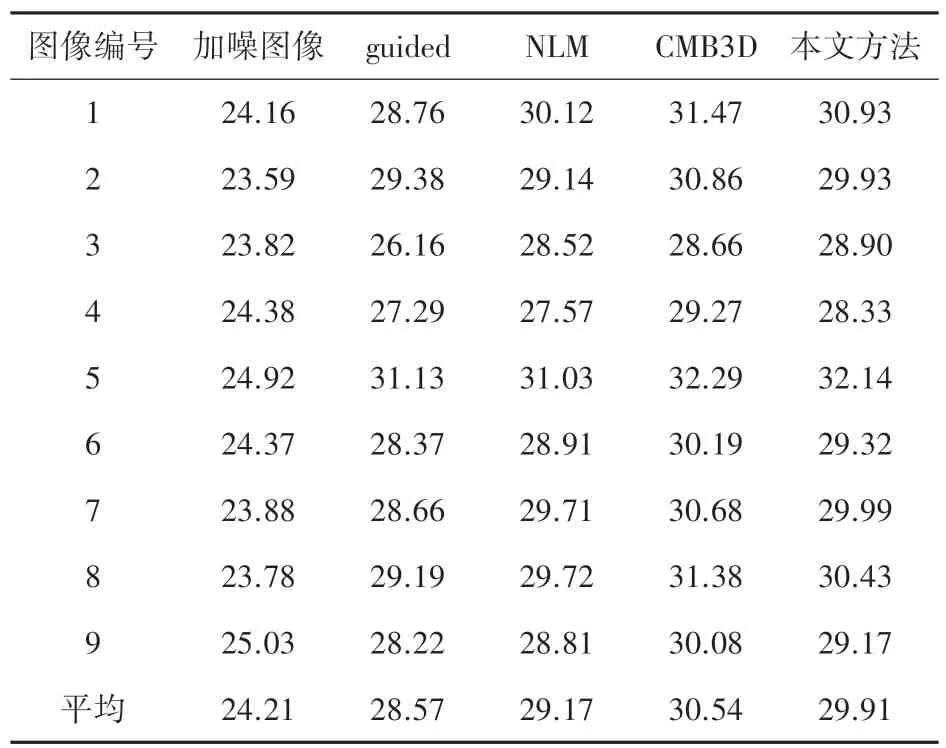
表1 不同算法去噪PSNR 比较Tab.1 Comparison of PSNRdenoising with different algorithms

4 结束语

本文提出了一种基于结构图像先验与ASM 能量的深度学习服装图像去噪方法。根据结构图像先验理论，卷积神经网络在生成图像时，图像中复杂的特征具有更大的阻抗，相较于图像中简单的特征在迭代后期才会生成。本文通过实验验证了图像中特征的复杂度与图像的ASM 能量之间具有正相关性。通过这一特性，可以根据网络生成图像的ASM 能量大小给定截止条件，即当生成图像的ASM 能量处于极大值时网络停止迭代，此时的输出图像即为去噪图像。实验结果表明，与guided、NLM 图像去噪算法相比，本文方法有更好的去噪效果，与CBM3D 图像去噪算法相比，本文方法有更好的实用性。本文方法相比传统图像去噪方法的不足之处在于需要大量的训练时间，未来工作将致力于设计性能更好的网络结构，以提高图片去噪效率与去噪效果。