沥青混凝土轨道床在温度荷载下的动力响应

【摘 要】文章采用有限元法，在不同热荷载下，将所述沥青混凝土设定为弹性和粘弹性的路基材料，通过钢轮给轨下基础结构施加一个动力荷载，模拟列车碾压轨道的过程，以对比分析材料在拉伸应变和垂直位移的计算结果。建立了不同热荷载、不同材料特性与拉伸应变和垂直位移的关系。采用云计算进行计算。计算结果表明，在相同的温度荷载下，粘弹性材料的拉伸应变和垂直位移均大于弹性材料。并且在较高温度（40 ℃）时，沥青混凝土层的拉伸应变和垂直位移都出现了大幅度的增加，轨下基础结构的可靠性降低。

【关键词】云计算; 沥青混凝土; 温度荷载; 动力响应

【中图分类号】U213.7+1【文献标志码】A

1 沥青混凝土轨道床

在过去的十年间，我国的铁路运输系统发展迅速。尤其是客运高速铁路的发展，其不仅在运营里程上超过世界其他国家高铁线路总和，其同样在速度、舒适性和运行密度上都取得了巨大的进步。但是，随着速度的提高，铁路运行的平稳性和舒适性仍待进一步的研究和优化，这可以通过优化运动动力学、优化铁路断面的质量和基床以下路堤的结构设计来解决。

由于沥青混凝土的诸多优点和特性，沥青混凝土轨道床在铁路建设中具有重要的作用，在中国、美国、德国、法国、意大利、西班牙、日本、韩国等国家的铁路施工中均有使用。包含多个结构层的轨道是铁路轨下基础结构中最基本的组成部分，因此，在铁路轨道系统中，对通过的移动荷载的动力响应的研究一直是铁路工程领域研究的重点和难点。在高速铁路轨道建设中，沥青混凝土轨道床由于具有降低高噪声、阻尼振动、抗竖向变形、将分布荷载传递至路基、增强路基的防水性及耐久性等诸多优势[1]而被工程界重视。

在传统的有砟轨道和无砟轨道的铁路基础设施建设中，研究人员在对沥青混凝土轨道床的研究中，在不同地区和环境下进行了数量可观的试验研究。Rose通过研究得出，在铁路基床以下路堤和道砟层之间加入沥青混凝土层可以有效提高铁路路基的柔韧性和抗疲劳特性，并且，与仅将沥青铺在表层防水相比，中间层的沥青混凝土能够抵消来自底层的疲劳开裂，并且使铁路轨道的使用寿命能够达到设计的50 a[2]，如图 1所示。

在解决铁路工程领域动力学相关问题中，由于有限元方法（FEM）在结构和动态仿真模型中已经取得了良好的一致性[3]，故而被广泛采用。在研究沥青混凝土路面结构的力学设计的过程中，采用胡克定律（Hooke’s law）描述的线性弹性模型是表征较低温度下沥青混凝土层动力响应的最合适的方法，然而，由于热拌沥青混凝土（HMA）材料的属性随温度的变化可以是弹性的，粘弹性的，塑性的或者三者的组合，因此很难尤其是在温度较高的情况下描述其行为。

随着时代的发展，云计算（Cloud Computing）在工程领域中的应用越来越广泛。云计算是分布式处理、并行处理和网格计算的发展，是一种利用互联网实现随时随地、按需、便捷的访问共享资源池的计算模式[4]。随着计算机科学技术的发展，独立的计算机终端设备的运算能力逐渐不能满足工程计算领域更精准，更高效的计算，计算能力从独立个人的终端向集中的服務器终端靠拢，并伴随着互联网、通讯技术的发展，计算服务产生了网络化、可扩展和按需服务的特性，云计算服务正是满足这些特性的技术[5]。与传统的计算机相比，相似配置的云计算机不仅能够最大限度的释放计算能力、降低能耗，更能摆脱地域环境的限制，让使用者在有网络覆盖的任何地方通过简单的终端连接到云计算服务器，完成相关任务，也能够在多人参与的工程项目中及时共享计算成果。本研究采用云计算技术，极大提高了模型计算的速率。

先前进行的大多数关于沥青混凝土的研究都没有考虑到材料性能对铁路轨道动力响应的影响，然而，对于沥青材料的行为，无论是弹性的还是粘弹性的，都会对运动荷载的动力响应有很大影响。但是，纵观各篇关于沥青混凝土的科学研究，很少有在对沥青混凝土层建模时考虑到沥青混凝土材料的温度特性对结果的影响。

为了研究轨下基础结构的动力响应，在恒定的移动载荷和不同的温度载荷下，采用有限元方法模拟该铁路轨道在高速列车运动下的模型。即，比较了在不同热荷载下沥青混凝土轨道床的弹性和粘弹性材料行为的中跨拉伸应变和垂直位移方面的模拟动力响应，以在模拟的动力响应中探究材料性能的差异。

2 研究材料和方法

2.1 在时域上的有限元分析

通常，铁路轨道系统动力响应的基本表达式为：

式中：[M]， [C]， [K]分别是该系统的质量、阻尼和刚度矩阵。ü（t），（t），u（t）分别是该系统的加速度、速度和位移矢量。F（t）是外力矢量。在本研究中，利用隐式直接积分动力分析方法计算铁路轨道的非线性动力响应。该方法基于有限元分析软件中的Newmark积分方法和Hilber-Hughes-Taylor方法（α-方法）。

2.2 对材料阻尼的建模

在非线性动力学建模中有必要使用真实的材料阻尼。弹性材料有一个能量耗散源，可以用阻尼比来模拟。可使用瑞利阻尼矩阵[C]来定义阻尼率，如下所示：

式中：[M]是模型的质量矩阵;[K]是模型的刚度矩阵;α是质量比例阻尼系数;β是刚度比例阻尼系数，可以分别从第i模态和第j模态的特定系数ξi和ξj确定所述系数。如果假设两个模态具有相同的阻尼比ξ，则上述系数可以用下列方程表示：

式中：ξ是临界阻尼比，而w1和w2是模态分析定义的固有频率。用来计算瑞利系数的两个频率可以作为结构的第一个固有频率。另外，为了确定模态的固有频率，研究建议首先使用第10模态形状以避免系统过度阻尼。但是，当材料被视为粘弹性材料时，不必使用瑞利阻尼系数。

2.3 热拌沥青混合料（HMA）的材料特性

HMA表现出多种取决于时间和温度的行为，沥青混凝土轨道床弹性材料是该行为分析的最简单模型。但是，HMA仅在低温或高速加载速率下表现出完全的弹性。因此，对于沥青混凝土材料而言，使用粘弹性材料的行为才能提供动力响应方面的准确结果。在本研究中考虑了两种类型的沥青混凝土层的材料性能，即弹性和粘弹性。表 1列出了沥青混凝土层的弹性材料特性。

在线性粘弹性材料特性的情况下，采用Prony级数描述广义Maxwell实体模型[6]。Prony级数可以在有限元软件的时域或频域中输入。沥青材料的Prony级数可以通过实验室测试确定，例如间接蠕变柔度试验和松弛或直接拉伸试验。可以表示为：

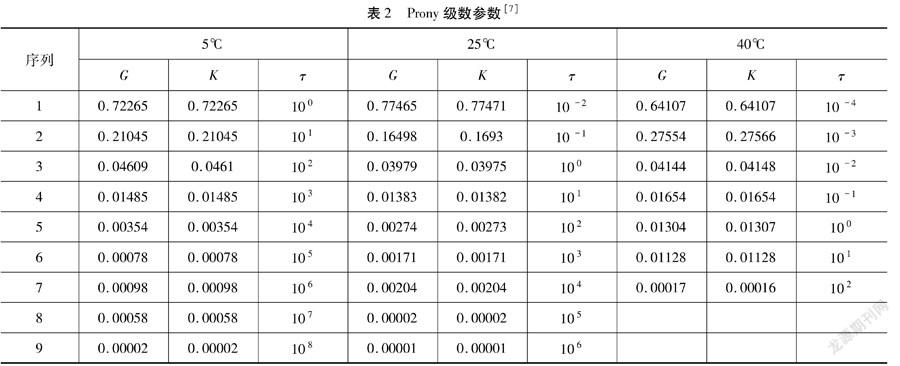
式中：Gt是在时间t的松弛模量;G0是瞬时模量; gi是Prony级数参数; τi是松弛时间;n是参数数量。表 2中提供了Prony参数[7]。Prony级数数量通常设置为5～11。G反映了无量纲的松弛模量;K反映了无量纲的体积松弛模量，τ是松弛时间。

2.4 铁路轨道的有限元分析

在云计算机运行的有限元分析软件上建立了含沥青混凝土层的铁路轨下基础结构在不同温度下的恒定移动荷载作用下的动力响应三维有限元仿真模型。在该模型中，将无砟轨道设计为钢轨、钢轨垫块、轨道板、水泥乳化沥青（CA）砂浆层、水泥混凝土支承层（PCC层）、基床表层、基床底层以及基床以下路堤的组合。使沥青混凝土层铺设在PCC层和基床表层层之间。仿真模型中采用的轨道几何形状和材料特性是基于在我国广泛使用的中国铁路轨道系统标准。由于该模型在轨道方向上是对称的，因此，在进行模拟试验时，仅考虑了一半的无砟轨道，如图 2所示。

除沥青混凝土层外，其余所有轨道组件均以具有各向同性弹性材料的实体单元建模。在仿真模型中，假定弹簧和阻尼元件位于钢轨和轨道板之间，其刚度值为6×107 N/m，阻尼系数为4.77×104 Ns/m[9]。每层均采用特定材料设计，其性能列于表3。

在非线性有限元分析中，有必要在节省时间和效率方面确保有限元模型的收敛性。使用粗糙网格的有限元模型能够较快完成运算，但是结果可能是不准确的。虽然精细的网格可能会提供较高准确度的结果，但需要花费大量时间和大量的数据存储。 因此，数据提取点设置在纵向长度中跨的沥青混凝土轨道床的底部的中点。所有分析均在具有3.0 GHz的计算频率，64 GB RAM和32核处理器的云计算机中运行。经过对比分析，在权衡精确度和计算成本后，试验采用尺寸为0.3 m的网格对模型进行网格化，

在使用有限元分析软件时，使用预定义的现生成的部件来定义分析过程中的恒定温度值。该预定义部件仅用于沥青混凝土层。

2.5 移动荷载的确定

在本仿真试验中，假定车轮沿钢轨表面平稳地行驶。采用面对面接触特性模拟具有硬接触和无摩擦切向接触特性的轮轨相互作用。

在不施加任何垂直动态激励的情况下，将集中的轮对负载（F=70 kN）施加到车轮的参考点上。该载荷是根据在我国广泛使用的CRH3列车轴载荷的静态解结合实际列车在动荷载过程中施加到钢轨上的作用力的统计结果的期望值得到的。车轮采用了刚体单元。负载模式如图2（b）所示。试验模拟车轮沿钢轨移动并转动。此外，钢轮行进距离为70 m，从一端的5 m开始，到距离另一端的5 m的点结束。

3 计算结果与分析

3.1 温度荷载对拉伸应变的影响

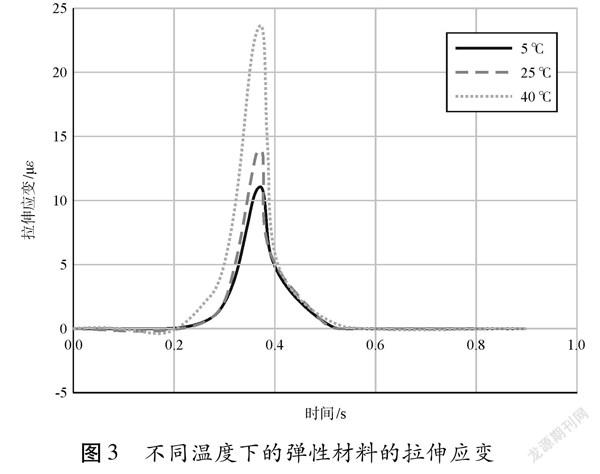
分别计算了在温度为5 ℃、25 ℃ 和40 ℃的情况下，沥青混凝土轨道床底部取样点处的拉伸应变。将取样点处的数据整理绘制出材料弹性和粘弹性行为的曲线图，如图 3和图 4所示。图 3表示材料在弹性行为下的拉伸应变，在5 ℃、25 ℃和40 ℃的温度下，拉伸应变的最大值分别约为6.34 με、9.61 με和14.98 με。计算分析表明，随着温度的升高，取样点处的拉伸应变逐渐增大，且其增长率也曾大。图 4表示材料在粘弹性行为下的拉伸应变，可以明显观察到，沥青混凝土材料的粘弹性和弹性在拉伸应变上表现出相似的变形过程。在5 ℃、25 ℃和40 ℃时取样点处的伸应变最大值分别约为6.44 με、9.70 με和26.44 με。

对比发现，粘弹性材料的曲线峰值明显大于弹性材料的峰值。将弹性和粘弹性材料在各温度下的应变峰值统计绘图，如图 5所示，在相同温度下材料表现出粘弹性行为的最大拉伸应变总是大于材料表现出弹性行为的最大拉伸应变。并且，当温度升高到40 ℃时，粘弹性材料的拉伸应变大幅度升高，这也表明了在较高温度下，沥青混凝土支承层存在较大的安全风险。

3.2 温度荷载对垂直位移的影响

本试验同样计算了在温度为5 ℃、25 ℃和40 ℃的情况下，沥青混凝土轨道床底部取样点处的垂直位移。计算结果如图 6、图 7所示。当沥青混凝土材料表现出弹性行为时，如图 6所示，在5 ℃、25 ℃和40 ℃时，取样点处的垂直位移分别为0.243 mm、0.256 mm和0.287 mm。与拉伸应变相似，随着温度升高，沥青混凝土材料的垂直位移增长率明显增大。图 7表示的是，当沥青混凝土材料表现出粘弹性行为时，在5 ℃、25 ℃和40 ℃的温度下，垂直位移分别约为0.244 mm、0.261 mm和0.297 mm。同样可以观察到，粘弹性材料的垂直位移曲线轮廓明显大于弹性材料的曲线轮廓。

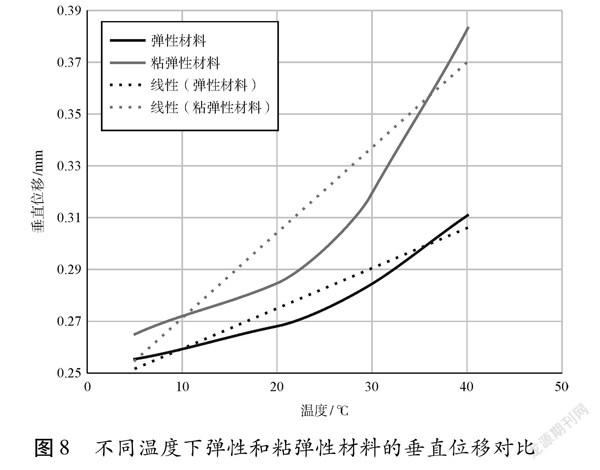
图 8量化了两种材料下垂直位移的差异，从曲线图的趋势可以得出，在相同温度下材料表现出粘弹性行为的垂直位移总是大于材料表现出弹性行为的垂直位移，并且这种差异是呈非线性增长的。

4 结论

本研究在云計算机环境下建立了沥青混凝土轨道床的三维有限元模型，通过在仿真模型中赋予沥青混凝土层相应的材料参数来设定其表现出弹性行为或粘弹性行为，以及通过改变材料参数模拟沥青混凝土在不同温度下的材料性能。研究了不同温度荷载对弹性和粘弹性的沥青混凝土层的拉伸应变和垂直位移的影响。经过整理和分析后得出以下结论：

（1）本研究建立的仿真模型能够很好地模拟在动荷载和温度荷载下，无砟轨道沥青混凝土层的拉伸应变和垂直位移，得出的计算结果较接近现实情况。

（2）通过对比分析计算结果，当沥青混凝土层表现出弹性行为时，随着温度的升高，沥青混凝土层的拉伸应变和垂直位移也随之增大，并且拉伸应变和垂直位移的增长率也在增加，即，温度越高，提高单位拉伸应变或位移的增量越大。

（3）当沥青混凝土变现出粘弹性行为时，其变化模式与其表现出弹性行为时相似。

（4）相同温度荷载下，沥青混凝土在表现出粘弹性行为时的拉伸应变和竖直应变都大于其在表现为弹性行为时的拉伸应变和竖直应变。

（5） 沥青混凝土在温度较低时更多表现为弹性行为，在温度较高时更多表现为粘弹性行为。

（6）本研究的模型相对真实的沥青混凝土轨道层有待更进一步的细化研究，例如考虑在更低温度下的弹性研究或者更高温度下的粘弹性研究，或者赋予沥青混凝土其他线性或非线性的弹塑性或粘塑性的材料特性等。

参考文献

[1]Yang E H， Wang K， Qiu Y J， et al.Asphalt Concrete for High-Speed Railway Infrastructure and Performance Comparisons[J]. Journal of Materials in Civil Engineering， 2016， 28（5）： 04015202.

[2]Rose J G， Bryson L S. Hot Mix Asphalt Railway Trackbeds[C]. International Conference on Perpetual Pavements， 2009：2-3.

[3]Kouroussis G， Connolly D P， Verlinden O. Railway-induced ground vibrations - a review of vehicle effects[J]. International Journal of Rail Transportation， 2014， 2（2）：69-110.

[4]劉鹏. 云计算[M]. 北京：电子工业出版社，2011.

[5]刘强. 基于与计算的BIM数据集成与管理计算研究[D]. 北京：清华大学，2017.

[6]梅生启. 混凝土静动态粘弹性能研究[D].北京：北京交通大学，2019：113-114.

[7]Yoo P， Al-Qadi I. Effect of Transient Dynamic Loading on Flexible Pavements[J]. Transportation Research Record Journal of the Transportation Research Board， 2015， 1990：129-140.

[8]Yoo P J， Al-Qadi I L， Elseifi M A， et al. Flexible pavement responses to different loading amplitudes considering layer interface condition and lateral shear forces[J]. International Journal of Pavement Engineering， 2006， 7（1）：73-86.

[9]Lei X. High speed railway track dynamics： algorithm and application[M]. Beijing， China： Science Press，2015.

[10]Fang M， Qiu Y， Rose J G， et al.Comparative analysis on dynamic behavior of two HMA railway substructures[J]. Journal of Modern Transportation， 2011， 19（1）：26-34.

[11]Fang M，Cerdas S F. Theoretical analysis on ground vibration attenuation using sub-track asphalt layer in high-speed rails[J]. Journal of Modern Transportation，2015;23：214-219.

[12]闫斌，谢浩然，沈青川，等.季冻区CRTSⅠ型无砟轨道不平顺规律及受力特性[J].哈尔滨工业大学学报，2021，53（3）：110-117.

[定稿日期]2021-01-13

[基金项目]国家自然科学基金（项目编号：51778541）

[作者简介]谭琪（1993～），男，在读硕士，研究方向为沥青混凝土材料。