引领学生“深度学习”的几种策略
2021-12-16黄良本
黄良本
《义务教育数学课程标准(2011年版)》指出:“作为促进学生全面发展教育的重要组成部分,数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能,更要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用。”为此,教学时,教师要引导学生进行深度学习,遵循数学学科特点、遵循学生成长规律,让数学学习在课堂自然地发生,体验知识的形成过程,促使学生大胆地猜测、深入地思考、主动探索课堂知识。
一、在问题驱动中进行深入探究
学习数学的价值在于它能有效地解决现实世界向我们提出的各种问题,而数学模型正是联系数学与现实世界的桥梁。只要有恰当的数学问题作引子,学生总能够在解决问题的过程中进行深入探究,解决数学问题。
如,在教学“租船问题”一课时,师出示:两位老师组织全班30名学生参加综合实践活动,举行划船活动,大船坐6人,每艘船要付30元;小船坐4人,每艘船要付24元;师生都要参加,那么,如何租船,才能最省钱?师:要想最省钱,应该选择租什么船?怎么租呢?生1:租小船,因为32÷4=8(条),刚好,不浪费座位。生2:租大船,因为大船每人付30÷6=5(元),小船每人要付24÷4=6(元),所以,要租大,租大船较便宜。生3:租6条大船,浪费4个座位,要尽量多租大船,再租小船,并且要尽量没有空位。师:这三种方案都各有理由,究竟哪种最省钱,需要通过计算来比较。
学生通过一系列计算、比较得出方案三最省钱后,教师让学生讨论如何快速有序找出最佳方案并计算费用:(1)24×8=192(元),(2)30×6=180(元),(3)30×4+24×2=168(元)。通过引导学生进行比较,逐渐建立最省钱的数学模型:大船价钱×大船数量+小船价钱×小船数量,租大船是最佳选择,应该优先考虑,且要省钱就不能有空位。
以“怎样租船,最省钱?”这个问题进行驱动,引领学生进行有序思考,积极探究,寻找解题方法与最佳方案,但这样一种基于数学问题的由无到有、由粗到精的过程,恰恰是学生数学思维、核心素养获得提升的基石。
二、在有效追问中进行深入理解
小学数学课堂中的追问应该是充满数学味的追问,才能避免学生思考欠缺深度或流于问题表象的情况。小学生对问题的回答往往没有经过认真思考,就“信口开河”或“人云亦云”,或缺乏深度,可以透过表面回答,追问学生的真实想法,让学生追寻思维的根源,继续深入地思考,弄清其中的道理。
如,教学“小数乘整数”一课时,先出示例题:每个风筝3.5元,3个风筝多少钱?引导学生进行列式,并指名汇报,有的学生用加法列式:3.5+3.5+3.5=10.5(元);有的学生用乘法列式:3.5×3=10.5(元)。師问:这是小数乘法,我们之前没学过,你是怎么算出来的?生回答:我是把3.5扩大10倍变成35,35×3=105,再把105缩小10倍,就是10.5。师又问:为什么这里的3.5可以变成35?生说:先把3.5元化为35角。这样可以把小数转化成整数,比较好算了。师:大家的分析有独到之处,能把新的问题转化成已经学过的知识来解决,这是一种很好的数学思想方法。
因此,教学时,学生往往不能很好地考虑好解答的每一细节,只是粗略地知道这样列式,教师可以通过一环扣一环地追问,在学生缺乏思考处牵一牵、引一引,将问题指向学生思维的深度,使其知其然,又能知其所以然。
三、在认知冲突中进行深度建构
在数学课堂教学中,教师可恰当制造认知冲突,巧妙设置情境,激活学生已有认知,促使学生获得数学知识本质的理解,助力课堂的深度学习。
如,在教学“有余数的除法”一课时,认识余数时,许多学生只停留在剩余的部分就是余数,为了让学生自主发现和理解余数是平均分后剩余且不够再分的部分,即余数小于除数的本质理解。在感知有余数的除法算式的意义上,设计了分草莓情境引出问题,抛出以思考为前提的操作活动。19个草莓5个5个圈,为什么剩余4个?3个3个地圈,为什么刚才可以剩4个,这次却不可以了?通过对这两个问题的剖析,对“不够一份”和“还够一份”的对比,使学生深刻地理解余数的意义,初步感知剩下的个数可能与什么有关,也就是余数和除数间的关系。
这样的设计意在学生易错点上制造认知冲突,让学生在思维碰撞与质疑争议中纠正错误认知,达到建构知识的目的,巧设认知冲突必会促进学生的深度学习,同时也给课堂带来活力和温度。
四、在操作体验中进行深度学习
美国的大卫·库伯指出:“让体验成为学习和发展的源泉。”小学数学教学中,建构体验学习模式,学生能更好地从现象看到事物的本质,增强教学效果,达到深度理解的学习目标。故而,教师应该强化学生对知识的自我体验、感知、感受和感悟,深入理解要学习的知识点,再进行实践和探索,从而实现对学习目标的深度理解,让深度学习真实发生!
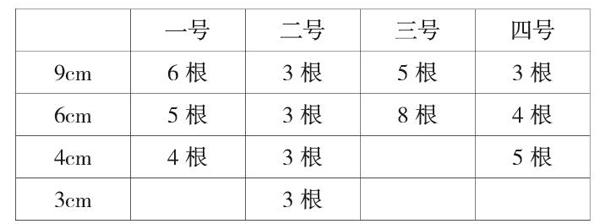
如,教学“长方体的认识”时,教师组织学生小组内动手操作,讨论交流哪一号的材料可以搭出长方体框架。
小组成员之间相互探讨,不断尝试,在动手操作中亲自感受不同长度小棒的组合,在实验、分析、思考中发现:(1)三组不同长度的小棒,每一组至少要有4根;(2)两组不同长度的小棒,有一组至少要有8根小棒,一组至少要有4根。
学生不再是被动接受知识,而是深度参与,积极体验,真正实现“自我发现的东西能积极地同化,从而产生深刻的理解”!不仅深化了对长方体棱特征的认知,也促进学生数学思维能力的提升!
