基于随机细观骨料的钢筋表面氯离子浓度概率分布研究
2021-12-16陈宣东梁秒梦虞爱平
陈宣东,荣 华,梁秒梦,虞爱平,明 阳
(1.桂林理工大学土木与建筑工程学院,桂林 541004;2.桂林理工大学,广西建筑新能源与节能重点实验室,桂林 541004; 3.中冶建筑研究总院有限公司,北京 100082)
0 引 言
氯离子侵蚀引起的钢筋锈蚀是海洋工程钢筋混凝土结构耐久性失效的主要因素之一[1-2]。海洋环境中的氯离子通过混凝土孔隙、裂缝等通道扩散到钢筋表面。当钢筋表面氯离子浓度达到阈值,钢筋表面钝化膜被破坏,进而诱发钢筋锈蚀,最终导致混凝土保护层开裂、脱落、结构失效[3-4]。因此,研究钢筋表面氯离子浓度分布对于海洋工程的健康监测、维护具有十分重要的意义。
近几十年来,国内外学者对氯离子扩散进行了大量的试验、理论和数值模拟研究[5-7]。Wang等[8]通过氯盐浸泡试验研究了氯离子在冻融循环下的氯离子扩散规律,研究表明冻融循环加速了氯离子扩散。为了探明海洋浪溅区混凝土中氯离子浓度分布特征,杨绿峰等[7,9]通过对现有的372组试验数据进行回归分析,建立了多因素下海洋浪溅区混凝土表面氯离子浓度的时变模型。金伟良等[10]研究了荷载行为对氯离子扩散性能的影响,研究表明当荷载达到混凝土极限荷载后,荷载对氯离子扩散具有显著影响。经过诸多学者[8,11-12]的不懈努力,发现氯离子在混凝土中的扩散遵循Fick第二定律。以上研究均是在确定性条件下进行。然而,混凝土材料本身具有各向异性和随机性等特点。在高政国等[13-14]提出的混凝土二维细观结构基础上,陈宣东等[12]研究了氯离子在混凝土细观结构中的扩散行为,研究表明钢筋表面氯离子分布是非均匀的、具有一定的随机性。余波等[15]根据钢筋表面氯离子浓度分布,建立了钢筋混凝土结构服役寿命预测的概率模型。程小康等[16]基于蒙特卡罗理论, 研究了氯离子扩散系数的概率分布,研究表明氯离子在混凝土中的分布具有明显的离散性。杨绿峰等[7]利用局部平均法,将混凝土的氯离子扩散系数随机离散为一组随机变量,建立了氯离子扩散分析的随机有限元法递归方程,研究了氯离子在混凝土中随机扩散的规律。混凝土中的氯离子分布对钢筋锈蚀分布及锈蚀形成的速率具有十分重要的影响;氯离子在钢筋表面呈现非均匀分布。氯离子的侵蚀,诱发了钢筋的电化学锈蚀,加速了钢筋锈蚀速率,进而加速了钢筋混凝土结构的耐久性失效。因此,有必要从混凝土细观结构层面,研究氯离子在混凝土中的随机分布。
本文基于混凝土细观结构模型和氯离子扩散理论模型,运用蒙特卡罗法,研究了钢筋表面氯离子浓度概率分布规律,建立了钢筋表面氯离子浓度分布概率密度函数,讨论了骨料分布对氯离子扩散的影响,以及骨料率对钢筋表面氯离子浓度概率分布密度函数的影响。
1 氯离子细观扩散模型
1.1 混凝土细观结构
混凝土是由骨料、砂浆、界面过渡区(interface transition zone, ITZ)等成分组成的多相复合材料。由于制作混凝土的材料和施工工艺水平具有随机性,混凝土材料的细观结构具有随机性。本文在高政国等[13]提出的凸多边形随机骨料算法基础上,引入界面过渡区且界面过渡区厚度随机分布,形成新的混凝土细观结构模型。具体流程如下:(1)根据高政国等的算法,生成不同粒径的凸多边形的骨料库,并记录凸多边形顶点到骨料中心的距离r;(2)在(1)的基础上,将凸多边形的各个顶点向凸多边形中心移动,移动的距离服从均值为60 μm、方差为10 μm的正态分布随机函数,进而形成骨料边界,骨料与砂浆之间的区域即为界面过渡区[17];(3)根据级配曲线,将带有界面过渡区的骨料库投放到矩形区域,当骨料率达到指定的骨料率时,终止投放。混凝土随机骨料形成过程的流程图如图1所示。值得注意的是,在骨料投放过程中,骨料之间的碰撞检查占用了大量的计算机内存和投放时间。本文通过COMSOL WITH MATLAB 接口,调用COMSOL命令集合,可极大缩短投放时间,减小计算及内存的使用。图2给出了骨料率为30%(体积分数,下同)和40%的混凝土随机骨料分布。

图1 混凝土随机骨料形成过程Fig.1 Formation process of random aggregate of concrete

图2 混凝土随机骨料分布Fig.2 Random aggregate distribution of concrete
1.2 氯离子扩散方程
国内外诸多学者[17-19]研究表明,氯离子在混凝土中的扩散符合Fick 第二定律。同时,根据混凝土的湿度条件,氯离子在混凝土中的扩散可分为氯离子在饱和混凝土中的扩散和氯离子在非饱和混凝土中的扩散。本文选择氯离子在饱和混凝土中的扩散作为研究对象。氯离子在混凝土中的扩散方程可以表示为[17]:
(1)
式中:t为侵蚀时间;x,y为空间坐标;Ci为自由氯离子浓度;下标i代表不同的相材料,分别是骨料、砂浆、界面过渡区(ITZ);Di为氯离子在i相中的扩散系数;Si为结合氯离子的浓度。根据Langmuir吸附曲线[20],结合氯离子浓度可以表示为:
(2)
1.3 氯离子扩散系数
国内外诸多学者对氯离子在砂浆中的扩散系数做了大量的试验研究,得出了诸多计算氯离子扩散系数的经验公式[21]。为了反映水灰比等因素对氯离子扩散性能的影响,本文采用Zheng等[22]提出的氯离子扩散系数计算方法。根据广义有效介质理论,初始氯离子扩散系数Dcp可以表示成:
(3)
式中:D0为氯离子在孔溶液中的扩散系数,1.07×10-10m2/s;Vp为砂浆的孔隙率。对于普通的波特兰水泥而言,水灰比和水化度是影响孔隙率的关键因素。根据试验数据,孔隙率可以表示为[22]:
(4)
式中:W/C为水灰比;α为水泥水化度,其范围为0~1。当水灰比小于0.5时,水化度可以表示为[22]:
α=1-exp(-3.15W/C)
(5)
由于骨料的壁效应,骨料边缘的水泥水化不充分,沿着骨料边缘,形成孔隙率较高的狭长区域,称为界面过渡区[19]。与砂浆区相比,界面过渡区的孔隙率是砂浆区的2~3倍[17]。更为重要的是,界面过渡区的孔隙连通性较好,而且曲折度较小。因此,界面过渡区促进了氯离子的扩散。基于试验数据,Pan等[23]建立了界面过渡区氯离子扩散系数与砂浆区氯离子扩散系数的关系式。界面过渡区氯离子扩散系数可以表示为:
(6)
式中:DITZ为氯离子在界面过渡区的扩散系数,m2/s;hITZ为界面过渡区厚度,μm。
无论对于界面过渡区还是砂浆区,混凝土的龄期和外界的环境温度都是影响氯离子扩散的重要因素。温度对氯离子扩散性能的影响,可以采用经典的Arrhenius方程表示[24],如式(7)所示:
(7)
式中:f(T)为温度影响系数;U为活化能,36.0 kJ/mol[22];R为气体常数,8.314 J·mol-1·K-1;Tref为参考温度,298 K;T为环境温度,K。
随着混凝土龄期增加,混凝土水化程度逐渐增加。新生成的水化产物堵塞了氯离子扩散通道,从而削弱了氯离子的扩散能力。混凝土对氯离子扩散系数的影响呈指数下降,其表达式如式(8)所示[17]:
(8)
式中:f(t)为混凝土龄期影响系数;t为氯离子侵蚀时间;tref为参考时间,28 d;m为时间衰减指数。
2 概率密度分布

图3 不同骨料分布的样本的氯离子浓度分布Fig.3 Chloride ion concentration distribution of samples with different aggregate distributions
当不考虑界面过渡区和骨料分布的影响时,在相同的侵蚀时间下,混凝土同一侵蚀深度处氯离子的浓度是相同的。然而,当考虑界面过渡区和骨料分布时,在相同的侵蚀深度下,由于骨料分布的随机性,混凝土各处氯离子的传输路径是不同的。因此,氯离子浓度在一定的区间内呈随机分布。为了研究骨料分布对混凝土中氯离子浓度分布的影响,本文数值模拟了3种不同骨料分布样本的氯离子浓度分布,其中样本的骨料率为40%,水灰比为0.4,侵蚀时间为10年。模型中采用的参数如表1所示。图3给出了不同样本在距离侵蚀面30 mm处,氯离子浓度沿x轴的分布曲线。从图3可以看出,在相同的侵蚀深度下,不同骨料分布样本的氯离子浓度是不同的。钢筋表面氯离子浓度是衡量钢筋混凝土结构耐久性的一个重要指标。因此,本文提出采用概率密度分布来表征钢筋表面氯离子浓度分布的状态。

表1 模型中采用的参数取值Table 1 Parameters used in the model
常见的概率密度函数有正态分布、伽马分布和对数正态分布等。本文通过蒙特卡罗法生成了6 000个混凝土随机细观骨料模型,并对每个模型进行氯离子扩散的模拟仿真,然后对各模型的氯离子浓度分布进行了统计。因此,本文采用实验概率密度分布统计方法,计算氯离子浓度的概率密度分布曲线。首先,将总体样本的最大氯离子浓度与最小氯离子浓度之差,平均分成n份。然后,记录样本数据落在每个区段的个数。因此,氯离子浓度的概率分布密度可以表示为:
(9)
式中:φk为第k个区间的概率密度;nk为落入第k个区间的样本个数;N为总的样本个数;ΔC=(Cmax-Cmin)/n为每个区间的氯离子浓度差值,Cmax为最大氯离子浓度,Cmin为最小氯离子浓度。
3 结果与讨论
3.1 骨料对氯离子扩散路径的影响
骨料的存在,改变了氯离子的传输路径。宏观上表现为氯离子在混凝土中分布的随机性。骨料率为40%、水灰比为0.4的样品被氯离子侵蚀10年时,其氯离子浓度分布如图4(a)所示。从图4(a)可以看出,氯离子的浓度分布是非均匀的。此外,在两个骨料之间的区域,氯离子出现了聚集现象。这主要是由于骨料具有低渗透性,氯离子扩散到骨料处,扩散受阻,所以出现聚集现象。因此,骨料的存在,缩小了氯离子扩散的通道,降低了氯离子的渗透性。图4(b)为氯离子扩散流线,由图4(b)可以清晰发现,骨料的存在增加了氯离子的扩散路径。例如,当氯离子从A点扩散到A’点时,在没有骨料的情况下,氯离子将沿着直线扩散(如图4(b)中的虚线所示)。然而,当骨料存在时,氯离子绕过骨料沿着曲线到达A’点,这增加了氯离子扩散路径的曲折度。由于骨料是采用Matlab随机生成,因此不同位置的骨料形态和大小各异,这也就导致了钢筋表面氯离子浓度在一定范围内随机分布。因此,钢筋表面氯离子浓度分布的随机性,是骨料随机性造成的。
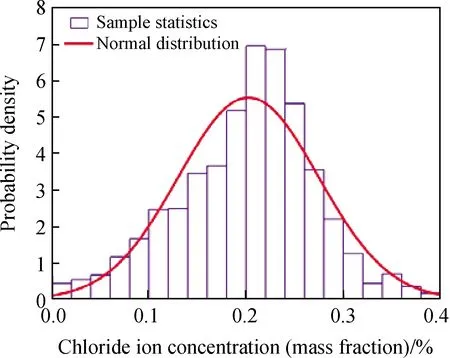
图5 概率密度分布Fig.5 Probability density distribution
3.2 氯离子浓度概率密度分布
骨料率为30%、水灰比为0.4的样品被氯离子侵蚀10年时,距离侵蚀面30 mm处的氯离子浓度概率密度分布直方图如图5所示。从图5中可以看出,氯离子浓度概率分布直方图两侧低、中间高,符合正态分布。同时,图5还给出了拟合的正态分布曲线(见图5中曲线)。从正态分布曲线可以看出,拟合的正态分布曲线与样本统计计算出的概率密度直方图形态相似。这表明骨料的随机性使得氯离子浓度分布服从正态分布,钢筋表面氯离子浓度概率分布可以采用正态分布来描述。通过对概率密度曲线积分,可以得到累计概率曲线(见图6中曲线)从累计概率曲线可以看出,统计的累计概率分布与正态分布的累计概率非常接近,这同样表明了骨料的随机性使得氯离子浓度分布服从正态分布。因此,钢筋表面氯离子浓度的概率密度函数可以采用正态分布来表征。
3.3 骨料率对氯离子浓度概率密度函数的影响
图7为骨料率分别为20%、30%和40%三种情况下,距侵蚀面35 mm处的氯离子浓度概率密度曲线。从图7中可以看出,随着骨料率变化,氯离子浓度概率密度曲线也发生了变化。当骨料率为40%时,氯离子浓度概率密度曲线呈现双峰形分布;而当骨料率为20%和30%时,氯离子浓度概率密度曲线呈现单峰形分布,且形态近似正态分布。这主要是因为骨料形态及骨料率均对氯离子浓度分布产生影响。当骨料率为40%时,骨料形态和骨料率均对氯离子浓度分布产生显著影响,因而氯离子浓度概率密度曲线呈现双峰形分布;而随着骨料率减小(例如骨料率为20%和30%时),骨料形态对氯离子浓度分布的影响逐渐削弱,因而氯离子浓度概率密度曲线呈现单峰形分布。Liu等[25]通过对不同骨料形态的混凝土细观模型数值模拟,对比分析了氯离子浓度分布的特征,也发现了类似的现象。进一步研究表明,骨料率为20%和30%的两条概率密度曲线,虽然形态相似,但是并不重合。通过计算可知,骨料率为20%和30%的样本,氯离子浓度的均值分别为0.246 4%和0.202 5%。随着骨料率增加,氯离子浓度的均值减小。这与3.1节骨料对氯离子扩散具有阻碍作用的研究结果相吻合,随着骨料率增加,氯离子扩散受阻影响增大。因此,表面氯离子浓度的统计均值较小。变异系数是衡量钢筋表面氯离子浓度离散程度的一个重要指标,它指的是钢筋表面氯离子浓度标准差与钢筋表面氯离子浓度平均值的比值。骨料率为20%、30%和40%的样本的变异系数分别为0.304 4%、0.356 0%和0.436 9%。随着骨料率增加,氯离子扩散路径的复杂程度也在增加,离散性增强。因此,变异系数随着骨料率的增加而增加。
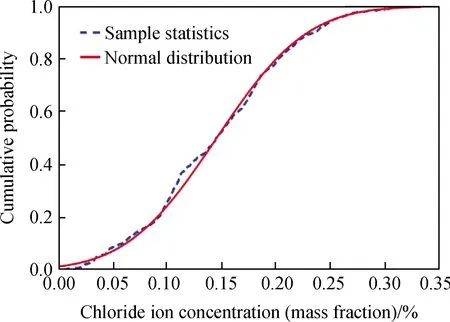
图6 累计概率分布Fig.6 Cumulative probability distribution

图7 不同骨料率的氯离子浓度概率密度曲线Fig.7 Probability density curves of chloride ion concentration with different aggregate ratios
4 结 论
(1)通过对现有的随机骨料的顶点进行外拓可形成界面过渡区,同时,采用Matlab调用 COMSOL命令集合,可快速判断骨料间的碰撞,节约计算资源。
(2)骨料对氯离子的扩散具有阻碍作用。骨料的存在,缩小了氯离子的扩散通道,造成了氯离子积聚,增加了氯离子扩散的曲折度和路径。
(3)骨料的随机分布造成了钢筋表面氯离子浓度分布的不均匀性。骨料率小于40%的混凝土,钢筋表面氯离子浓度服从正态分布。随着骨料率增加,氯离子浓度概率密度函数的均值逐渐减小,而变异系数逐渐增大,钢筋表面氯离子浓度的离散性增强。
