半导体制冷床垫睡眠热平衡系统模拟与性能分析
2021-12-16邢佳康赵载文罗勇强
陈 勰 邢佳康 赵载文 罗勇强
(华中科技大学环境科学与工程学院 武汉 430074)
建筑消耗的能源约占总能源消耗的20%~40%[1]。其中,空调系统的能耗占据建筑能耗的40%~50%[2]。因此,降低空调系统能耗成为节能减排的重要环节。为满足人体在室内的热舒适,传统空调系统需要对整个空间进行冷却或加热处理,不仅会造成大量的能源消耗,房间内还会存在温度分布不均等情况,造成人体不舒适[3]。在夏季,随着全球变暖的加剧以及城市热岛效应,环境温度升高,更加重了空调系统的负担[4]。H.Pallubinsky等[5]指出局部的制冷系统营造的非均匀热环境可成为有效替代方案。并且局部的制冷系统可以准确满足人体热舒适需求,避免了传统空调系统中温度分布不均带来的供需不平衡问题。
人约有三分之一的时间在睡眠中度过,良好的睡眠质量将有助于身心健康。L.Lan等[6]利用布置有毛细冷水管的毯子对人体进行局部制冷,研究发现该系统可提高人的睡眠质量。Li Xiaxia等[7]研究了不同床垫类型以及不同冷却方式对人热舒适和睡眠质量的影响。Qian Xiaolei等[8]对睡眠期间人体的5个不同部位分别进行局部制冷,发现改善热舒适最有效的途径是在背部进行局部冷却。这些实验研究的侧重点是人体睡眠热舒适及睡眠质量,缺乏对局部制冷的节能性与人体睡眠热舒适的综合模型与分析研究。半导体被认为是一种资源节约和环境友好的小型热泵,它没有运动部件,因此也不会产生噪音,可靠性高,响应快[9],并且可以精准控制温度[10]。A.Rincón-Casado等[11]提出一种利用热电制冷的温控床垫,输入90 W的功率可使床垫的温度低于周围环境温度2.1 ℃,但该研究并未从人体与床垫耦合换热的角度进行模型研究。
本文利用半导体器件的优良特性,搭建了基于半导体制冷的睡眠热平衡系统实验平台,并建立了半导体制冷与人体热负荷耦合的系统传热模型,模型的准确性通过了实验数据的验证,在此基础上进一步分析了系统的温度分布和人体热平衡状态。相比于以往研究,本文将半导体传热模型和人体睡眠热负荷模型进行耦合,综合考虑了不同热环境、半导体工作电流、结露问题等影响因素。
1 模型建立
1.1 半导体制冷床垫传热模型
半导体制冷床垫如图1所示,主体为铝板,铝板尺寸为1 800 mm×600 mm。床垫周围和背部铺设保温材料,10个半导体均匀布置,在每个半导体背后有散热器相连。
为得到床垫的温度分布情况,采用基于有限差分的传热建模方法,主要内容包括:
1)划分网格。
如图1所示,对于模型而言,图中浅蓝色区域即可出反映整个床垫的温度分布,故将这一区域定为典型区域,并划分网格。

图1 半导体制冷床垫Fig.1 Thermoelectric-based cooling mattress
2)传热系数确定。
对流换热表面传热系数hc(W/(m2·K))通过式(1)和式(2)计算[12]:
(1)
(2)
式中:Nu为努塞尔数;Ra为瑞利数;g为重力加速度,m/s2;α为体积膨胀系数,1/K;Δt为室内温度与床垫平均温度之差,℃;l为定型尺寸,m;Pr为普朗特数;v为运动黏度,m2/s;λa为空气导热系数,W/(m·K)。
辐射传热系数hr通过式(3)~式(5)计算[13]:
hr=5×10-8[(AUST+273)2+
(Tm+273)2][(AUST+273)+
(Tm+273)]
(3)
AUST=Tin-3z
(4)
(5)
式中:AUST为面积加权平均温度,℃;Tm为床垫平均温度,℃;Tin为室内温度,℃;Tf为室外温度,℃。
3)迭代计算。
采用控制容积法,将床垫视为由很多个微元体构成。每个微元体都会受到与它相邻的4个微元体的传热,同时会以辐射和对流的形式与环境换热。若该微元体与半导体相连,还会与半导体进行换热。若微元体处没有半导体,则会通过保温材料与外界换热。所以需要分别讨论不包含半导体的微元体和包含半导体的微元体。涉及的相关参数如表1所示。

表1 传热分析参数Tab.1 Parameters of heat transfer analysis
对于不包含半导体的微元体,式(6)为热平衡公式,可化简为式(7):
(6)
(7)
对于包含半导体的微元体,式(8)为热平衡公式,可化简为式(9):
(8)
(9)
式中:Δx、Δy、Δz分别为微元体在x、y、z方向上的长度,m;t为微元体的温度,℃;Δτ为时间步长,s;Qc为半导体制冷量,W。其他参数如表1所示。
因为采用向前差分,为保证计算值的稳定,必须满足式(10)条件。所以本模拟在网格划分后,在满足式(10)的条件下设置时间步长为1 s。
ρcΔx2Δy2-2λΔτ(Δx2+Δy2)≥0
(10)
半导体制冷量依据式(11)和式(12)计算[13]。已知图1 中T1及Tf,可以联立式(11)和式(12)求解Tc、Th,从而得出每一时刻的制冷量:
(11)
(12)
式中:Qh为半导体散热量,W;Tc为半导体冷端温度,℃;Th为半导体热端温度,℃;I为半导体工作电流,A。其他参数见表1。
1.2 人体睡眠热负荷模型
为了定量化描述人体横躺在床垫上时,环境和系统参数对人体热舒适的影响,本文使用Lan Li 等[14]提出的二区域模型进行人体传热建模。该二区域模型将人体分为与床垫接触和不与床垫接触两个部分进行建模。通过人体热负荷(定义为人体产热量和损失热量的差值)计算式(13)可以预测人体的冷热感觉,利用式(14)计算人体表面积:
3.074×10-3(1-β)(5 520-p)-
(13)
AD=0.202M0.425H0.725
(14)
式中:L为人体热负荷,W;p为吸入空气水蒸气分压力,Pa;AD为人体表面积,m2;β为与床垫接触的面积和人体表面积之比;T0为操作温度,℃;Rcl为睡眠覆盖物热阻,(m2·K)/W;fcl为覆盖面积系数;h为传热系数,W/(m2·K);Qbody为人与床垫换热量,W;M为体重,kg;H为身高,m。
模型中,假设人体身高为1.8 m,体重为70 kg,人体处于平躺状态,与床垫接触的皮肤表面积为整个皮肤表面积的0.39倍。在铝板上铺设一层薄床垫,薄床垫厚度为0.5 cm,导热系数为0.147 W/(m·K)。假设人体在睡眠状态下,穿着短袖衣,并盖上一张毯子,毯子只与人体接触,不与床垫接触。衣服及毯子总热阻为0.6 (m2·K)/W。覆盖面积系数为94.1%[15]。操作温度和空气温度相同,相对湿度为50%,空气流速小于0.15 m/s,传热系数为8.335 W/(m2·K)。
1.3 半导体制冷与人体热负荷耦合模型
在计算人体热负荷时,由于人与半导体制冷床垫系统有换热,会改变床垫温度分布,从而影响人的热平衡。因此半导体制冷床垫模型和人体热负荷模型需耦合计算。首先计算得到与床垫接触的皮肤表面积,并划分出与人体换热以及不与人体换热的微元体。对于与人体换热的微元体而言,以辐射和对流形式与环境的换热量将变成与人体的换热量,如式(15)所示(以不包含半导体的微元体为例)。对于不与人体换热的微元体而言,以辐射和对流形式与环境的换热量将变为通过薄床垫的传导热量,如式(16)所示(以不包含半导体的微元体为例)。由此可得床垫的温度分布。
(15)
(16)
式中:λs为薄床垫导热系数,W/(m·K);δs为薄床垫厚度,m。
本文基于python语言建立了半导体制冷与人体热负荷耦合模型。首先依据微元体的热平衡公式对床垫的温度分布进行计算,通过判断各微元体温度随时间的变化情况,得到稳态时床垫的温度分布。此时将微元体与人体的换热量累计求和,可得到总换热量Qbody,将Qbody带入式(13)中,即可计算得到人体热负荷。
2 模型验证
模型模拟了1.4 A恒定电流情况下,床垫表面的非均匀温度场。室内室外温度如图2(a)所示,室外温度在31~38 ℃内变化,室内温度在(25±2)℃范围内波动。模型与实验的对比主要针对半导体制冷床垫。半导体制冷床垫模型的验证结果如图2所示,主要对比图1中T1、T2、T3三点的温度。由图2可知,模拟的变化趋势和实验测试的变化趋势相近,误差控制在2 ℃以内。1点的误差相对2、3点大,平均绝对误差为0.68 ℃,2点和3点的平均绝对误差分别为0.40 ℃和0.42 ℃。整个床垫的平均绝对误差以三点的实验、测试平均值计算得到,平均绝对误差为0.22 ℃。因此,模拟和测试的结果吻合较好,半导体制冷床垫的温度分布模拟具有可靠性。对于人体热负荷模型,Lan Li等[14]利用模型计算了睡眠时的中性温度,与实验测试相比,误差小于5%。

图2 室内外温度以及T1、T2、T3实验测试与模型模拟温度变化对比Fig.2 Indoor and outdoor temperature,comparison of experiment and simulation at T1,T2,T3
对耦合模型进行误差分析。当人体热负荷为0时,可由式(13)和式(15)计算得到中性温度,如式(17)所示。半导体制冷床垫模型存在的误差会传递到间接测量量中性温度上,如式(18)和式(19)所示,计算得到中性温度计算的误差为±0.89 ℃。在中性温度范围为25~30 ℃时,相对误差控制在3.56%以内。之后通过和人体热负荷模型的误差合成,耦合模型的误差在8.56%以内。
(17)

(18)

(19)

3 系统分析
3.1 环境和系统参数影响
图3所示为在不同室内温度与不同工作电流条件下,人体热负荷的变化情况。由图3可知,随着半导体工作电流的增加,热负荷逐渐减少。且在电流大于3 A时,热负荷基本不变,甚至缓慢上升,说明床垫和人体的换热基本不变,过大的工作电流反而会由于有限的散热器散热能力,影响半导体制冷。
当室内温度不断升高时,人体热负荷也不断升高,Lan Li等[14]提出4个等级的睡眠热舒适环境,其中等级二为正常水平,此时人体热负荷为(-3.3,3.3),即图3中的灰色区域。当未开启半导体制冷床垫,即电流为0 A时,室内温度为25 ℃和26 ℃,人体感到舒适。但在开启制冷床垫之后,通过调节工作电流大小,在室内温度略高于28 ℃时也能保持舒适。这表明通过半导体制冷床垫营造的非均匀热环境,舒适的室内温度范围可以扩大约2~3 ℃,避免了不必要的空调能耗。

图3 不同室内温度及不同电流下人体热负荷Fig.3 Thermal load of the body in different indoor temperature and current
由于是局部制冷装置,在有半导体的微元体附近,温度会稍低。在计算人体热负荷时,可从理论上分析人体和床垫的换热量能否满足热舒适需要,但在实际应用过程中,非均匀温度场与低温区域可能会引起人体局部过冷,造成不舒适。所以,需要讨论床垫的温度分布情况。半导体制冷装置在室内温度为27、28、29 ℃,电流分别为1、2、3 A时床垫典型区域的温度分布如图4所示。由图4可知,室内温度越低,电流越高,床垫低温区的温度越低。在这3种室内温度情况下,制冷床垫温度可以低于环境温度4~8 ℃。在电流为1、2、3 A时,表面最大温差分别约为3.1、4.9、5.5 ℃。随着电流的增大,床垫表面温度不均匀性增强。减小电流输入将有利于温度场均匀性的改善。
3.2 半导体制冷床垫设计优化
局部制冷还需要讨论的另一个问题是结露问题。床垫温度分布如图4所示,中心温度最低,该位置最容易结露。在不同室内温度条件下,电流为1、2、3 A时,表面结露的临界相对湿度分别约为64%、48%、44%,表明当相对湿度高于临界相对湿度,床垫最低温度处将结露。在半导体工作电流为2 A或3 A时,存在较大的结露风险。因此,需要对系统进行设计优化处理。

图4 不同室内温度及不同电流下半导体制冷床垫典型区域温度分布Fig.4 Temperature distribution at the typical region in different indoor temperature and current
由于床垫较大的结露风险,有必要进行优化设计,在提高床垫最低温度的同时还要满足舒适需要。模拟计算表明,随着电流的增大,床垫表面温度不均匀性加剧,为了使床垫温度分布更均匀,且同样达到热平衡状态,可以在增加半导体数量的同时减小电流。在优化设计中,将典型区域内半导体器件增至4个均匀布置,如图5所示。

图5 优化后的半导体制冷床垫Fig.5 Thermoelectric-based cooling mattress after optimization
采用半导体制冷与人体睡眠热负荷耦合模型对优化后的半导体制冷床垫进行分析,环境和系统参数与系统优化前设置一致,人体热负荷模拟结果如图6所示。由图6可知,在优化后,由于半导体器件数量的增加,在相同室内温度时,更小的电流输入即可达到热平衡状态。同时,图6中曲线呈单调下降趋势,说明在一定工作电流范围内,散热器的散热能力不会影响半导体制冷。此外,优化前室内允许的舒适空气温度范围为25~28 ℃,优化后舒适空气温度范围扩大至25~29 ℃。

图6 优化后不同室内温度及不同电流下人体热负荷Fig.6 Thermal load of the body in different indoor temperature and current after optimization
半导体制冷床垫设计优化后典型区域温度分布如图7所示。由图7可知,电流为1 A时,优化后平均温度降低约7 ℃,表面最大温差约为1.7 ℃,降低约1.4 ℃。当电流为0.3 A和0.5 A时,表面最大温差约为0.6 ℃和1.0 ℃,优化后系统的表面温度均匀性显著改善。
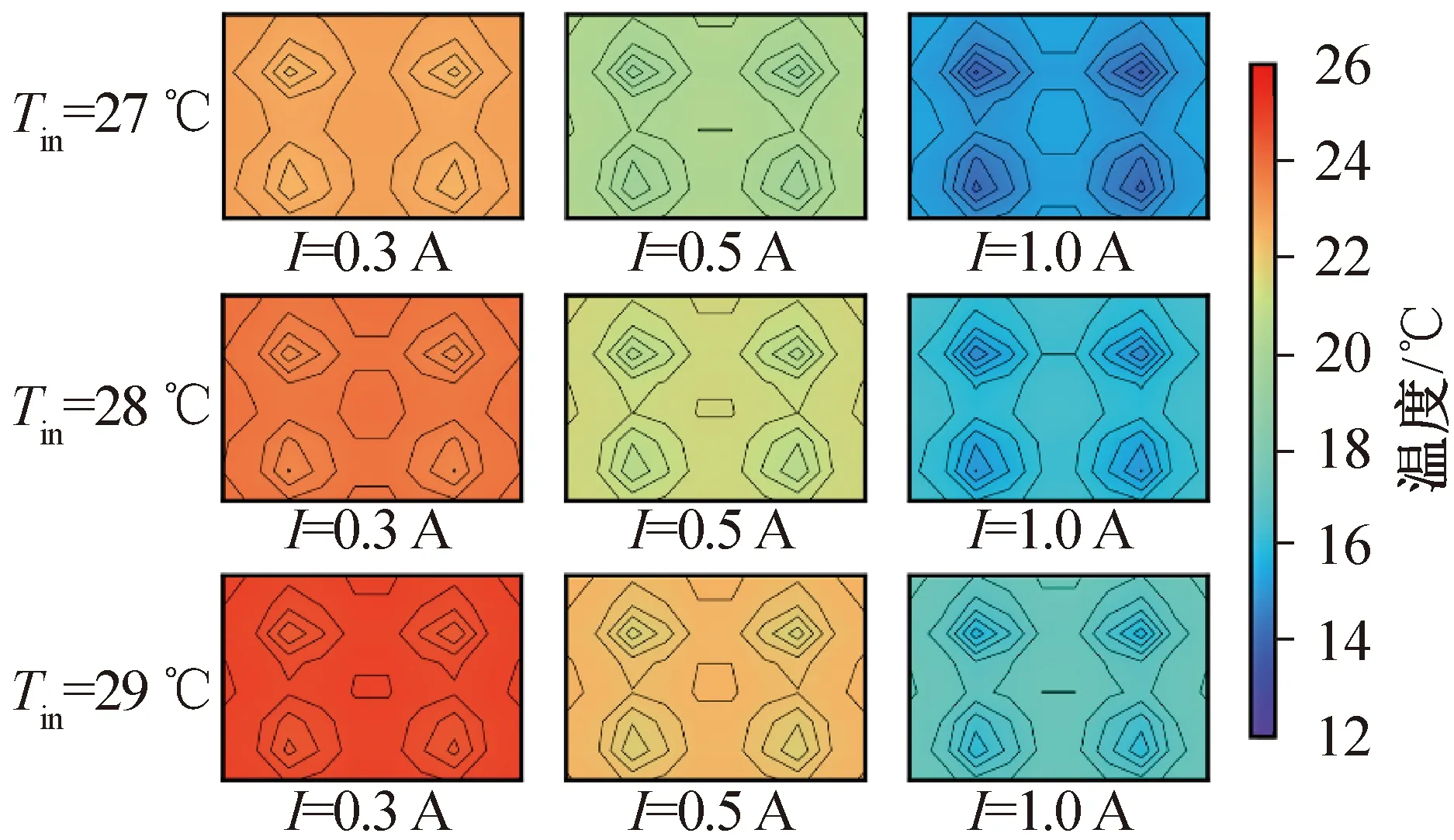
图7 优化后不同室内温度及不同电流下床垫温度分布Fig.7 Temperature distribution at the typical region in different indoor temperature and current after optimization
在防结露性能方面,在不同室内温度条件下,工作电流为0.3、0.5、1.0 A时,表面结露的临界相对湿度分别约为75%、63%、44%。优化前后同样的电流情况下,临界相对湿度有所降低。但优化后可以以更小的电流实现热平衡,相比于优化前,在同样满足热平衡的基础上,将表面结露的临界相对湿度提升10%~25%,模型的设计优化改善了结露问题。
综合考虑人体热平衡、床垫温度分布均匀度以及防结露性能,优化后的床垫虽然在29 ℃时增大电流输入可以满足舒适要求,但其较差的温度分布均匀度和防结露性能影响实用性。控制输入电流在0.5 A以内,保证较好的温度分布均匀度和防结露性能,室内允许的舒适空气温度最高可达约28.5 ℃。
3.3 系统节能性分析
为了研究优化后半导体制冷床垫的节能效益,模拟分析了某住宅中一间卧室的冷负荷。该住宅位于武汉,处于夏热冬冷地区,房间类型为中型,有一名成年男子居住。因为半导体制冷装置是在睡眠时开启,所以讨论的时间范围为23∶00—07∶00,共8 h。睡眠期间没有灯光散热。这间卧室有一面南外墙,一扇南外窗,外窗采用白色布窗帘进行内遮阳,其余三面是内墙,相邻房间是通风良好的非空调房间,层高为3 m。房间为矩形,南外墙的长度分别为4、6、8 m,矩形另一条边长度为4 m保持不变,通过改变南外墙的长度来实现对不同房间面积的讨论。围护结构的热工指标如表2所示,选取的围护结构均满足JGJ 134—2010 《夏热冬冷地区居住建筑节能设计标准》[16]。空调系统电功率通过冷负荷除以COP得到,夏季空调COP取值为2.8[17]。冷负荷选取为房间逐时冷负荷中最大值。

表2 围护结构热工性能参数Tab.2 Thermal performance parameters of building envelope
在开启半导体制冷床垫时,半导体需要消耗能源,通过式(20)计算。半导体热端的散热量在实际应用中通过改进装置排放到室外,不影响室内热环境,因此该处不考虑半导体散热量。分析节能率时,研究不同室内温度、半导体工作电流以及房间面积的影响。半导体工作电流的确定以满足热平衡和防止结露为准。
P=sI(Th-Tc)+I2R
(20)
房间冷负荷及节能率如表3所示。根据图6所示,利用空调制冷将室内温度控制到26 ℃时,人体达到热平衡状态,此时未开启半导体制冷床垫,设为参考工况。在室内温度控制为27 ℃和28 ℃时,人体不处于睡眠热平衡状态,因此同时开启了半导体制冷床垫进行局部制冷,分别为研究工况1及研究工况2。由表3可知,研究工况比参考工况更为节能,且节能率随着房间面积的增大而增大。在研究工况1,节能率在工作电流为0.3 A,房间面积为32 m2时最大,为10.26%。在研究工况2,节能率在工作电流为0.3 A,房间面积为32 m2时最大,为23.37%。

表3 不同室内温度、工作电流和房间面积下冷负荷及节能率Tab.3 Cooling load and energy saving ratio under different indoor temperature,current and room area
在冷负荷计算中,夏季空调室外计算日平均温度采用了历年平均不保证5 d的日平均温度。夏季空调室外计算干球温度采用了历年平均不保证50 h的干球温度。即计算的室外环境是较为炎热的,但大部分时间,室外温度并未达到模拟温度。
蓝玉良[18]检测了武汉市的昼夜气温特征,夏季夜间室外温度约在21~32 ℃范围内波动。当室外温度较低,室内温度能够维持在26~29 ℃时,可不进行空调制冷,仅开启半导体制冷床垫。假设室外温度为28 ℃,此时室内温度和室外温度相同,单独开启半导体制冷床垫能达到热平衡,当电流为0.5 A时,能耗约为28 W。而开启空调制冷,控制室内温度为26 ℃时,冷负荷在16 m2的房间内为315 W,空调消耗电功率为112.5 W。相比较而言,单独使用半导体制冷床垫的节能率为75%。如果房间面积增大,电流减小,节能率将更大。综上所述,半导体制冷床垫节能率与室内温度、半导体工作电流以及房间面积直接相关。
4 结论
本文搭建了基于半导体制冷的睡眠热平衡系统实验平台,并对该系统进行了热特性分析、设计优化、结露问题讨论以及节能性评价,得到如下结论:
1)本文建立了半导体制冷与人体热负荷耦合传热模型。半导体制冷床垫传热模型基于有限差分法,与实验测试的误差在2 ℃以内;人体热负荷模型误差在5%以内。耦合模型的误差控制在8.56%。模型精度较高,能预测床垫温度分布及人体睡眠热平衡状态。
2)通过增加半导体数量对制冷床垫进行优化,可以利用更小的工作电流实现热平衡,减小床垫温差,舒适的室内空气温度范围由25~26 ℃扩大为25~28.5 ℃。此外,在相同的热平衡状态下,优化后的制冷床垫临界相对湿度提高了10%~25%,降低了结露风险。
3)半导体制冷床垫具有良好的节能潜力。节能率随室内温度的降低、工作电流的减小、房间面积的增大而增大,最高可达23.37%。
本文受中央高校基本科研业务费专项资金(2019kfyXJJS189)资助。(The project was supported by the Fundamental Research Funds for the Central Universities (No.2019kfyXJJS189).)
