嵌入热管强化相变蓄冷板释冷性能的研究及优化
2021-12-16马翠玲陈雨虹郭丽媛邵双全朱婷婷孙志利
田 绅 马翠玲 陈雨虹 郭丽媛 邵双全 朱婷婷 孙志利
(1 天津商业大学 天津市制冷技术重点实验室 天津 300134;2 华中科技大学能源与动力工程学院 武汉 430074)
在线上与线下融合的消费“新零售”模式驱动下,生鲜冷链服务市场规模迅速增长[1]。随之增长的高频次、多品类冷藏运输业务对小型化、轻量化的冷能供给装备提出了迫切的市场需求[2]。蓄冷板作为一种便携式供冷单元,能够有效满足中短途冷藏运输轻量化用冷需求,受到冷链物流行业的广泛关注[3-4]。
蓄冷板以液-固相变材料作为冷能储存介质,可通过充/释冷过程的非连续性及其便携式特点协调冷藏运输过程中的冷能供给,是一种经济可行的用冷技术[5]。同时,由于利用了相变材料潜热大以及相变温度稳定的特点,蓄冷板还具有储冷密度高和控温精准的优点[6]。然而,面对当前更加复杂且多变的冷藏运输需求,蓄冷板在实际应用中仍面临一些适应性问题:1)液-固相变材料的导热系数普遍较低[7],使得蓄冷板内部的相变传热过程缓慢,导致在实际应用中普遍存在蓄冷板不能及时充/释冷从而影响物流周转的情况;2)在高频次的冷链配送过程中,冷藏箱内的瞬时负荷波动明显,难以被忽略,如:T.Lafaye de Micheaux等[8]实验测试了冷藏车箱体在开门后的渗风负荷,对于容积为32.4 m3的箱体且内外温差为40 ℃的情况,渗风的峰值显热负荷可达到100 kW以上,并在20 s内使箱体内的平均温度上升了40 ℃。对于相变蓄冷板,主要与箱体内空气发生换热,而空气的传热性能较差,结合蓄冷板内部相变材料的缓慢融化进程,使得蓄冷板对箱体内峰值热负荷难以做到快速响应。因此,为强化蓄冷板充/释冷过程以快速平衡热负荷波动,蓄冷板整体的传热性能还有待进一步提升。
为实现相变蓄冷板释冷过程的快速响应,国内外学者的研究主要通过增大相变材料与外界传热流体之间的传热面积,如在相变材料内部嵌入金属翅片[9]、泡沫金属[10]以及内嵌热管[11]等方式,强化蓄冷板整体传热性能。其中,将热管嵌入相变材料内部是一种高效可行的解决方案[12]。一方面,热管是一种具有高传热特性的元件,通过热管的传热驱动,可以增强相变材料内部的相变传热过程,以获得对冷能需求的快速响应。另一方面,热管本身无运动部件,整体结构紧凑且形式多样,适合与蓄冷板结合。然而,将热管嵌入蓄冷板后,蓄冷板整体传热过程具有一定复杂性,特别是在热负荷波动较大的情况下,空气-热管-相变材料之间传热过程的动态变化显著,使得蓄冷板在大温差负荷工况下的响应能力难以准确预测和量化,对该种形式蓄冷板的优化设计与实际应用提出了挑战。
综上所述,本文实验研究了热管嵌入式相变蓄冷板在大温差负荷条件下热管侧的动态释冷过程,并基于热阻分析方法搭建了用于分析空气-热管-相变材料之间动态传热过程的解析模型,模拟分析了热管布置方式及结构参数对动态传热过程的影响,为热管嵌入式相变蓄冷板的设计和应用提供理论指导。
1 热管侧释冷过程实验
1.1 实验系统及工况
实验系统如图1所示,主要分为6个部分:环境实验箱、真空箱、蓄冷板、风道、热管和蓄冷材料(水)。其中,蓄冷板内部尺寸为长×宽×高=180 mm×80 mm×160 mm。蓄冷板内嵌入了6支带毛细芯的铜-甲醇热管并横向布置为两排。热管管排间距为40 mm,热管外径为12.7 mm,热管壁厚为0.3 mm,毛细芯厚度为0.05 mm。热管的蒸发段暴露在外部空气中,长度为80 mm,上部冷凝段浸没在相变材料中,长度为68 mm。此外,热管蒸发段布置有翅片,整体传热面积为0.021 m2。蓄冷板放置在真空箱内,因此,蓄冷板内部传热过程主要由热管驱动,用于对空气-热管-相变材料之间的动态传热过程进行独立分析。
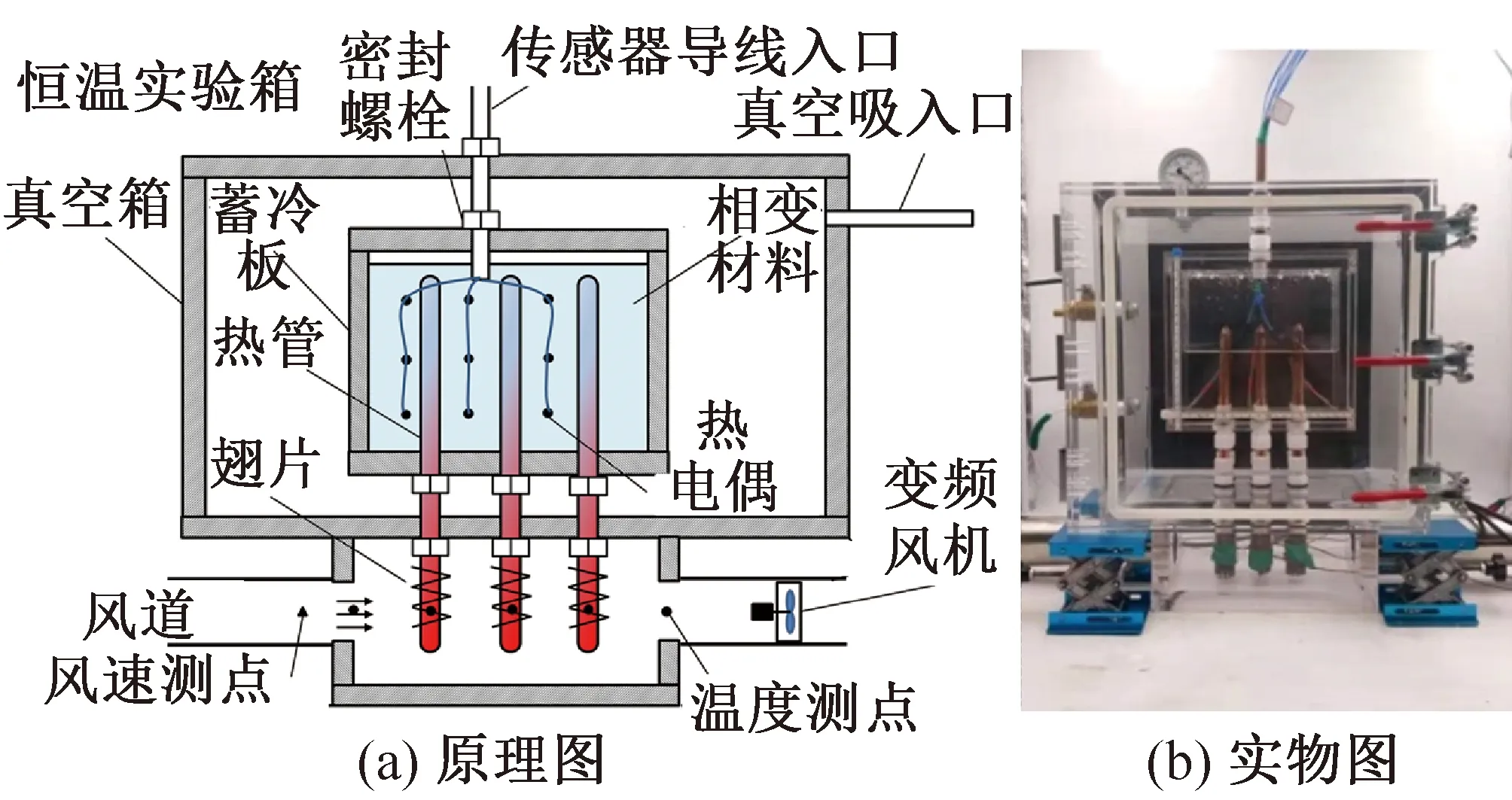
图1 实验系统Fig.1 The experimental system
本实验利用T型热电偶(经恒温水浴标定,精度:±0.1 ℃)进行测温,温度测点位置如图1所示。利用热线风速仪(精度:±5%,测量范围:0.2~20 m/s)测量风速,并采用规范提出的圆形风道风速标准测量方法[13],测量风道截面处12个点的风速值并计算得到平均风速。
实验围绕蓄冷板热管侧在高热负荷条件下的释冷性能开展,因此,对真空箱底部的风道设置了一系列较高送风温度以及3种不同风速。
1.2 实验数据处理
1)热管侧平均传热速率计算方法
由于蓄冷板外壁面采用真空绝热,因此忽略蓄冷板外壁面的传热过程,认为蓄冷板的瞬时传热速率等于风道进出口空气的显热差,热管侧瞬时传热速率计算式如下:
(1)
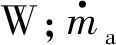
将上述实验测得的瞬时传热速率按时间积分得到蓄冷板总释冷量,再通过总释冷量与总耗时的比得到蓄冷板的平均传热速率。
2)不确定度分析
实验中直接测量参数包括进出口风温Tin、Tout,风速v(m/s),以及实验装置几何尺寸等参数,间接测量参数为瞬时传热速率,对以上参数测量结果进行不确定度分析,其中不确定度分量来源于随机效应和系统效应。对于温度采用送风温度测量值进行分析,平均风速采用12个测点的标准方差进行表征,几何尺寸采用测量仪器的相对不确定度进行计算。对于间接测量参数采用如下置信度为95%的扩展不确定度进行表征。
σ=2×
(2)
式中:σ为扩展不确定度;Δ为各参数的合成不确定度;R为几何尺寸测量值,m。
1.3 实验结果
1)蓄冷板平均传热速率
对应不同实验工况,蓄冷板平均传热速率如表1所示。由式(1)可知,瞬时传热速率主要与质量流量和温差有关,实验测得的平均传热速率随平均风速及送风温度的增大而增加,在送风温度为50 ℃时,平均传热速率最高可达42.50 W。
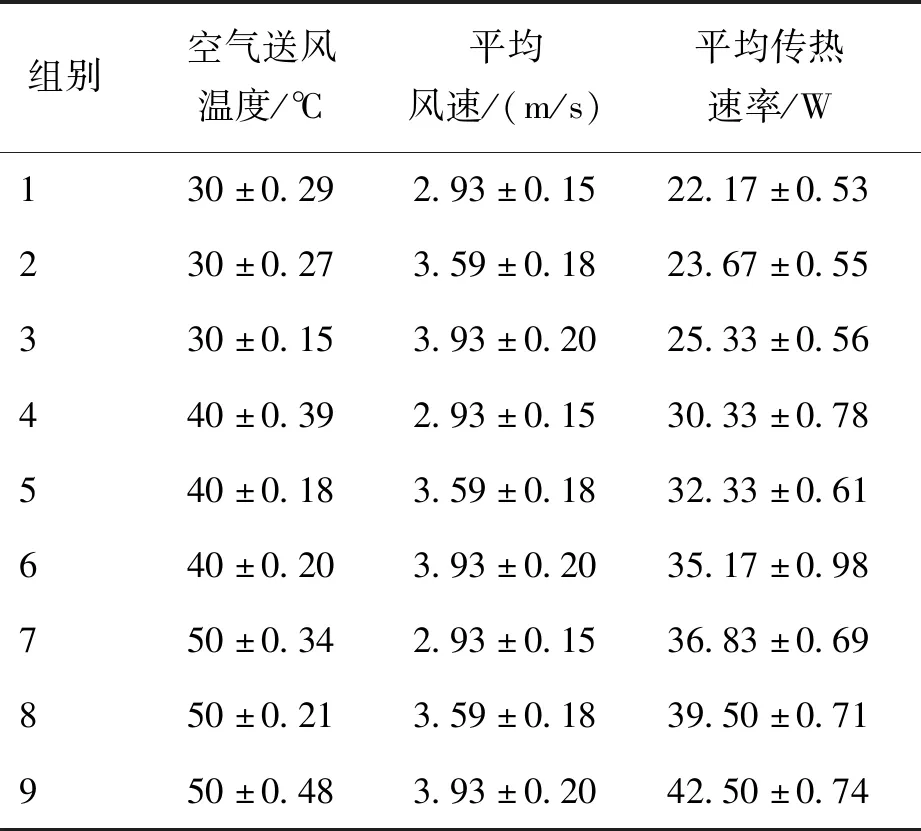
表1 不同送风温度和风速下蓄冷板的平均传热速率Tab.1 Average heat transfer capacity of the cold storage panel with different inlet air temperature and air speed
2)空气侧进出口温差的变化
图2所示为实验工况下进出口温差随时间的变化。由图2可知,各工况下空气侧进出口温差随时间逐渐减小且动态变化显著,说明在大温差负荷下,相变材料的动态融化过程对于热管侧的传热过程有重要影响。此外,在同一进风温度下,风速越大,空气侧进出口温差越小,但蓄冷板整体融化时间也随之缩短,表明风速越大,蓄冷板的瞬时传热速率越大,根据式(1),说明在同一送风温度下,质量流量的变化对瞬时传热速率的影响大于温差的变化。
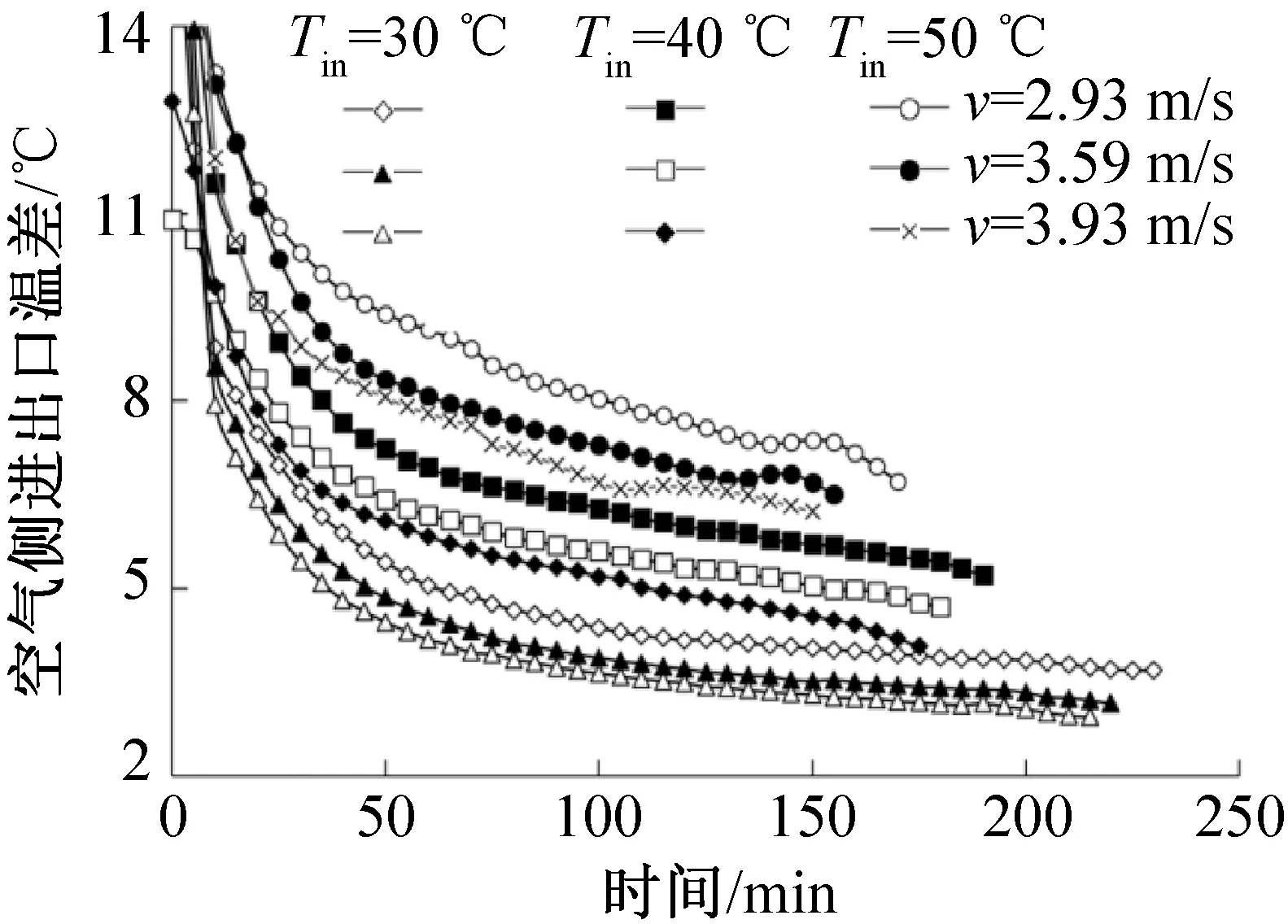
图2 空气侧进出口温差随时间的变化Fig.2 Transient variation of the temperature difference between inlet and outlet of airside
2 动态传热模型
2.1 整体传热过程模拟模型
本文以单根热管及其冷凝段和蒸发段的整体传热过程为传热单元开展模拟研究,传热单元如图3所示。热管一端暴露在空气中并通过翅片增大与空气侧的传热面积,热管另一端嵌入相变材料内部。在蓄冷板释冷过程中,热管与空气换热一端作为蒸发段,相变材料内部的热管段作为冷凝段。
为建立动态传热模型,本文采用热阻分析法,传热单元的各项热阻分布如图3所示。同时,考虑到相变传热过程的特性,本文在模型搭建过程中作出如下假设:
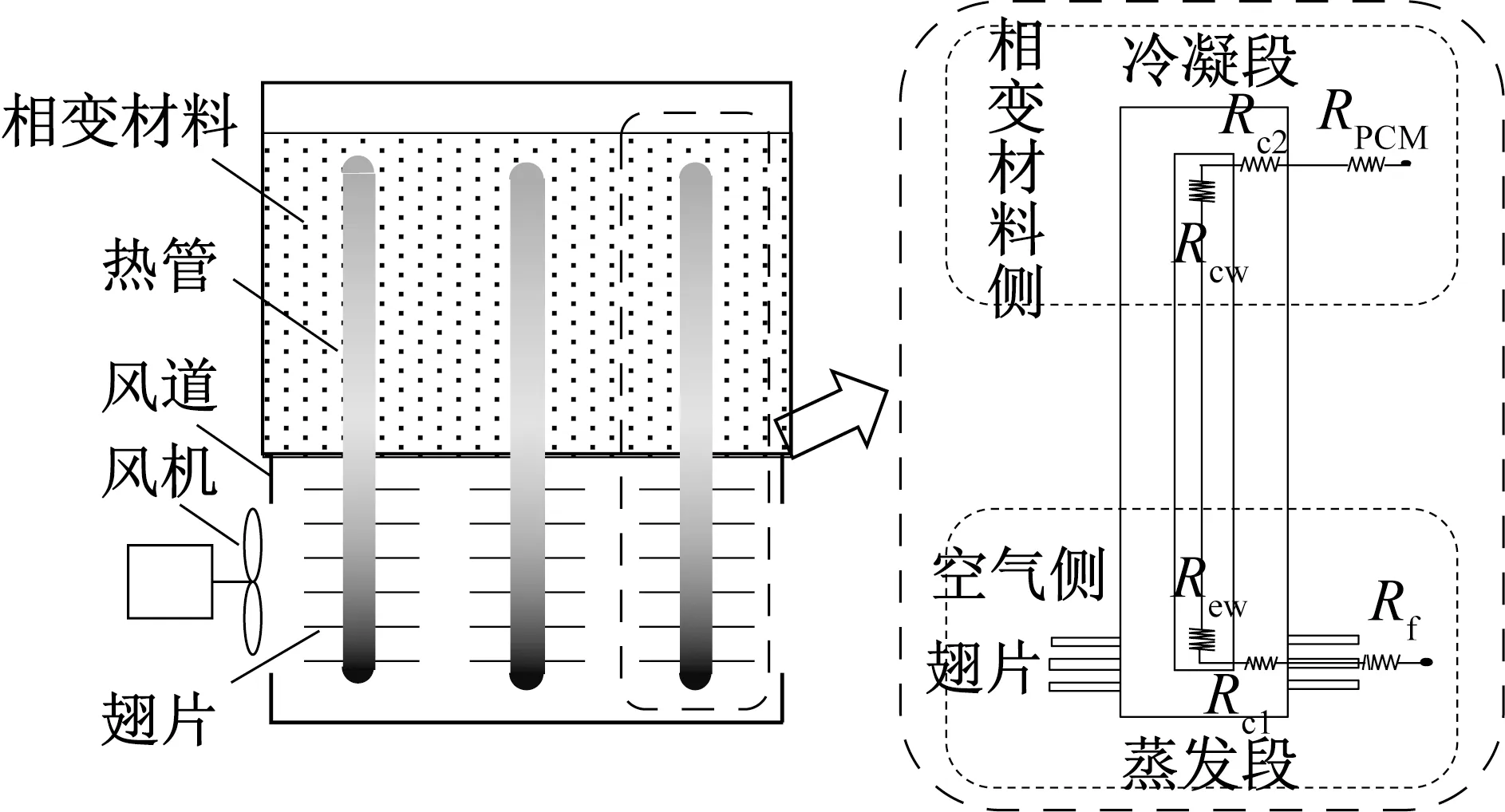
图3 传热单元及热阻分布Fig.3 Distribution of heat transfer unit and thermal resistance
1)由于液-固相变材料的潜热远大于显热,在发生相变时,相变材料液-固界面处的温度几乎不发生变化[14-15],因此,模型忽略相变材料的显热传热部分,认为传热过程由潜热主导;
2)本文所采用的热管为圆柱形,认为热管壁面传热均匀,相变材料在相变过程中的液-固界面呈圆环形;
3)由于采用了多根热管排布,认为相变材料液-固界面的最大半径位于相邻热管距离的中心点处;
4)液-固界面为可移动边界,其位置随时间发生变化。
根据上述假设,传热单元的能量守恒方程如式(3)所示,该式的物理意义为相变材料瞬时潜热变化量等于空气侧的瞬时传热速率。
(3)
式中:ρp为相变材料密度,kg/m3;γ为相变材料单位质量相变潜热,kJ/kg;V为相变材料体积,m3;Tin、Tout分别为空气侧的进、出口温度,℃;t为时间,s。
引用传热效率ε的表达式,式(3)可转化为:
(4)
(5)
式中:ε为传热效率;Tp为相变材料的相变温度,℃。
由于在传热过程中,传热单元一侧发生了相变,因此,根据ε-NTU方法,ε的表达式为:
ε(t)=1-exp[-NTU(t)]
(6)
传热单元数NTU的表达式为:
(7)
式中:RTotal为传热单元的总热阻,K/W。
式(3)~式(7)建立了传热单元总热阻与相变材料体积变化率之间的关系,在计算得到各项热阻以及输入空气侧进口温度后可使整个传热模型可解。
由图3可知,传热单元的总热阻由6个子热阻组成,其中,由于热管内部的传热过程主要由两相流体流动实现,传热效率高,可忽略热管内部的流动热阻。由此,总热阻RTotal表达式为:
RTotal=Rf+Rc1+Rew+Rcw+Rc2+Rp
(8)
式中:Rf为空气的流动热阻,K/W;Rc1为蒸发段热管壁热阻,K/W;Rew为蒸发段芯部热阻,K/W;Rcw为冷凝段芯部热阻,K/W;Rc2为冷凝段热管壁热阻,K/W;Rp为相变材料的热阻,K/W。式(8)中各热阻的具体表达式如表2所示。
综合式(3)~式(8)以及表2中的各热阻公式,可构建一个常微分方程组(ODE),在输入空气侧入口温度Tin后可对该方程组进行求解。对于蓄冷板的释冷过程,本文利用MATLAB软件中的ODE45函数对上述方程组进行求解,计算结果包括相变材料在融化过程中的环形液-固界面半径rpl,瞬态传热效率ε和空气侧出口温度Tout。

表2 各项热阻计算公式Tab.2 Calculation formula of thermal resistances
2.2 释冷过程模拟模型
对于蓄冷板的释冷过程,其特殊性在于相变材料融化后的导热系数的确定,即式(8)中Rp。该热阻项计算涉及的导热系数keff在释冷过程中为液相导热系数。但根据前人的研究发现,相变材料释冷过程中液相部分存在自然对流,对于整体传热过程有重要影响,因此提出了有效导热系数的概念。C.W.Chan等[16]在蓄冰球的传热过程研究中发现,相变材料的有效导热系数与瑞利数(Ra)有关。N.A.M.Amin等[17]基于Ra提出了一个具有较好普适性的有效导热系数经验公式,如式(9)所示。式(9)适用于水及盐溶液的有效导热系数计算。
keff/kpl=3.847 5×10-8Ra+1.585 9
(9)
本文采用式(9)计算蓄冷板内部释冷过程时液相部分的导热系数,并用于模型求解。
2.3 模型验证
1)空气侧进出口温差的模拟验证
由式(3)可知,空气侧进出口温差(如图2所示)对于描述蓄冷板的瞬时供冷量具有重要意义。因此,模型验证部分首先对该温差进行模拟研究。模拟计算采用了实验系统实际参数及实际工况,模拟与实验对比结果如图4所示。需说明的是,模型中送风温度的设置与实验工况一致,在模型计算中保持恒定。

图4 不同风速下空气侧进出口温差的验证结果Fig.4 Validation results of temperature difference between inlet and outlet of air side under different air velocity
由图4可知,温差在初始阶段的动态变化特征显著,模型计算的动态温差结果与实验值吻合较好,最大偏差为-0.52 ~ 1.19 ℃,说明本文提出的动态传热模型具有较高的模拟准确度。同时,模拟结果的准确性在很大程度上还依赖于相变材料有效导热系数公式的引入,在不考虑该系数的情况下,模拟结果的准确性较差。在各实验工况下,模型所使用的有效导热系数主要与Ra有关,即与相变材料内部的传热温差有关,模型计算中假设热管壁面与相变材料液-固界面间的传热温差为15 ℃,通过式(9)计算得到各工况下的有效导热系数如表3所示。

表3 实验工况下模型所用的有效导热系数Tab.3 Effective thermal conductivity utilized by the model with various experimental conditions
2)总释冷量的模拟验证
实验所用的相变材料为水,质量为1.8 kg,由于蓄冷板外壁面处在真空条件下,忽略蓄冷板壁面传热,认为实验测得蓄冷板在释冷过程中的总释冷量为1.8 kg×333 kJ/kg=599.4 kJ。同时,动态模型可计算得到蓄冷板瞬时传热速率,如式(10)所示,用于积分得到模拟的总释冷量。模拟与实验的对比结果如表4所示,模拟计算误差在-3.21%~6.16%之间,说明该模型具有较好的准确性。

(10)
3 模拟分析
由于本文所研究的蓄冷板内嵌入了热管,因此,热管的几何尺寸及布置方式对蓄冷板的整体传热性能有重要影响。在模型搭建和验证的基础上,本文利用所提出的动态传热模型分析了热管管排数、热管外径以及热管蒸发段长度对蓄冷板瞬时传热速率的影响。具体模拟分析参数如表5所示。
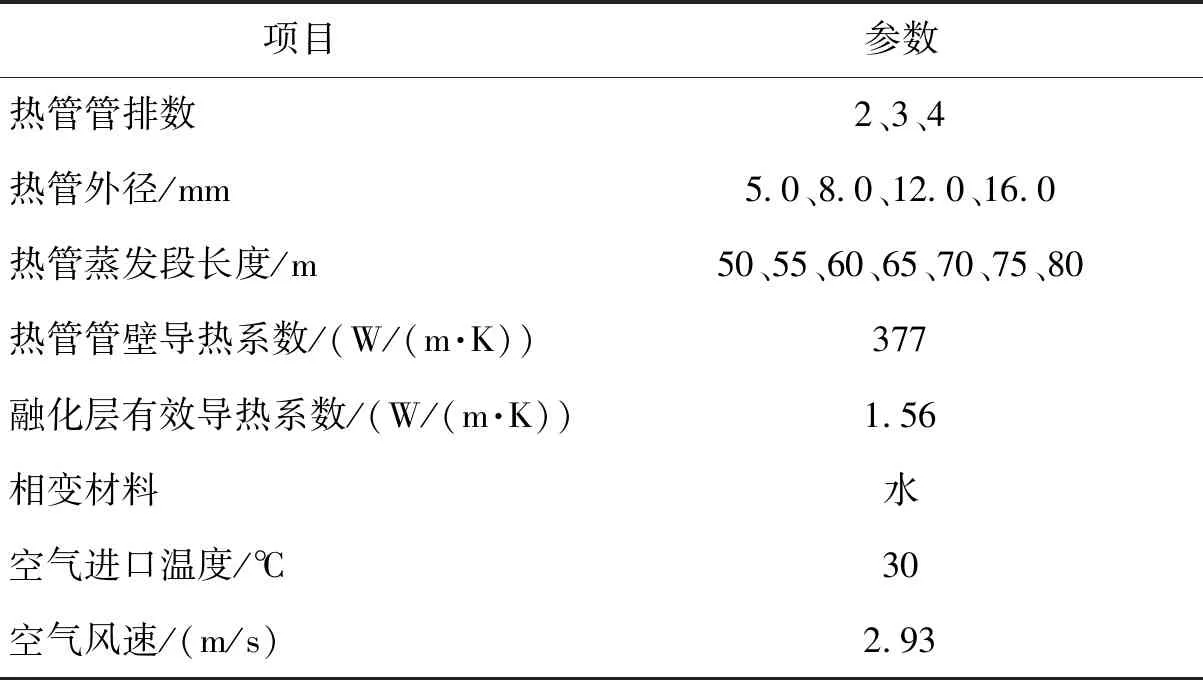
表5 模拟分析的具体参数Tab.5 Specific parameters for simulation analysis
根据以上模拟参数,蓄冷板瞬时传热速率的计算结果如图5~图6所示。
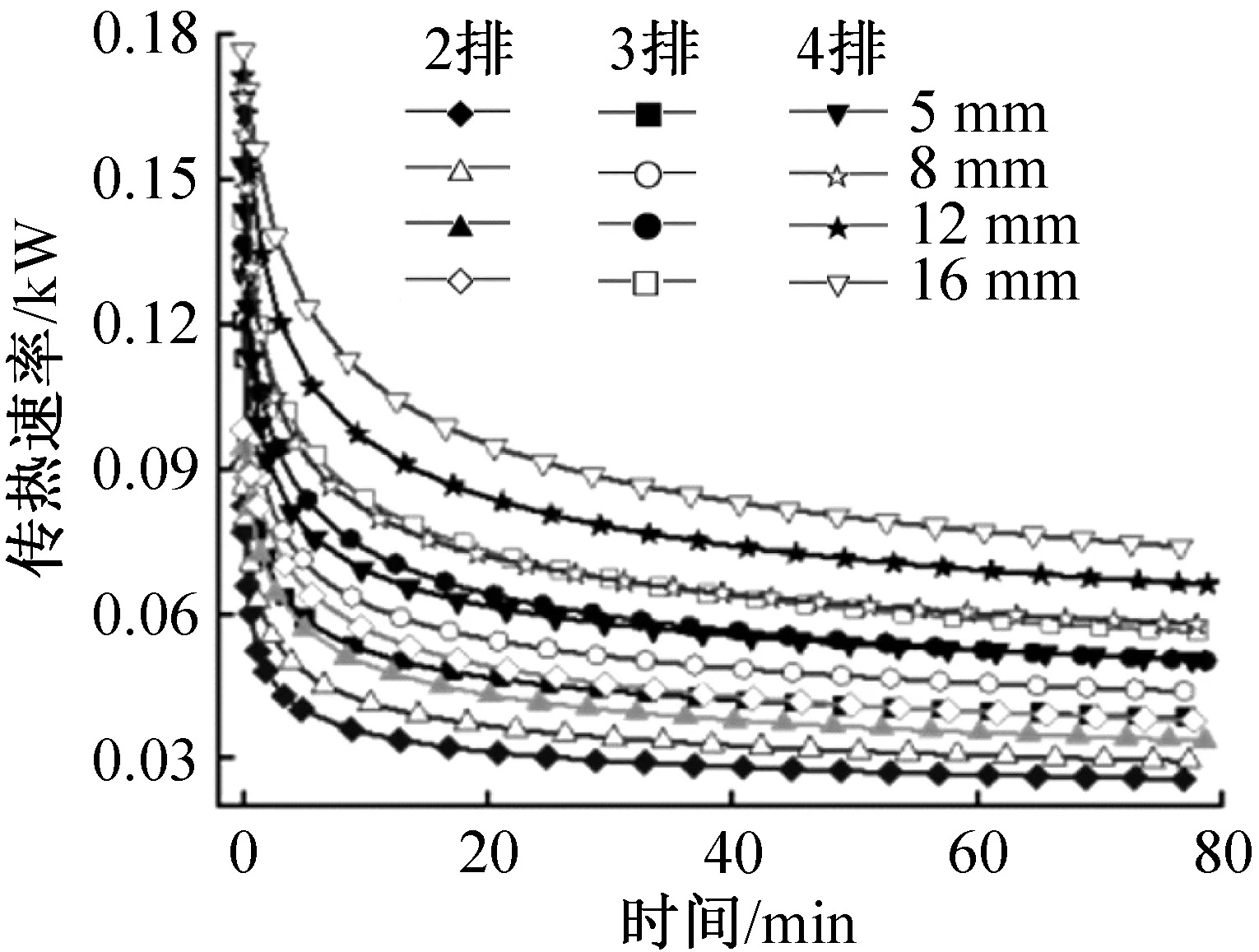
图5 热管外径和管排数对瞬时传热速率的影响Fig.5 Effect of outer diameter and number of tubes on the transient heat transfer rate
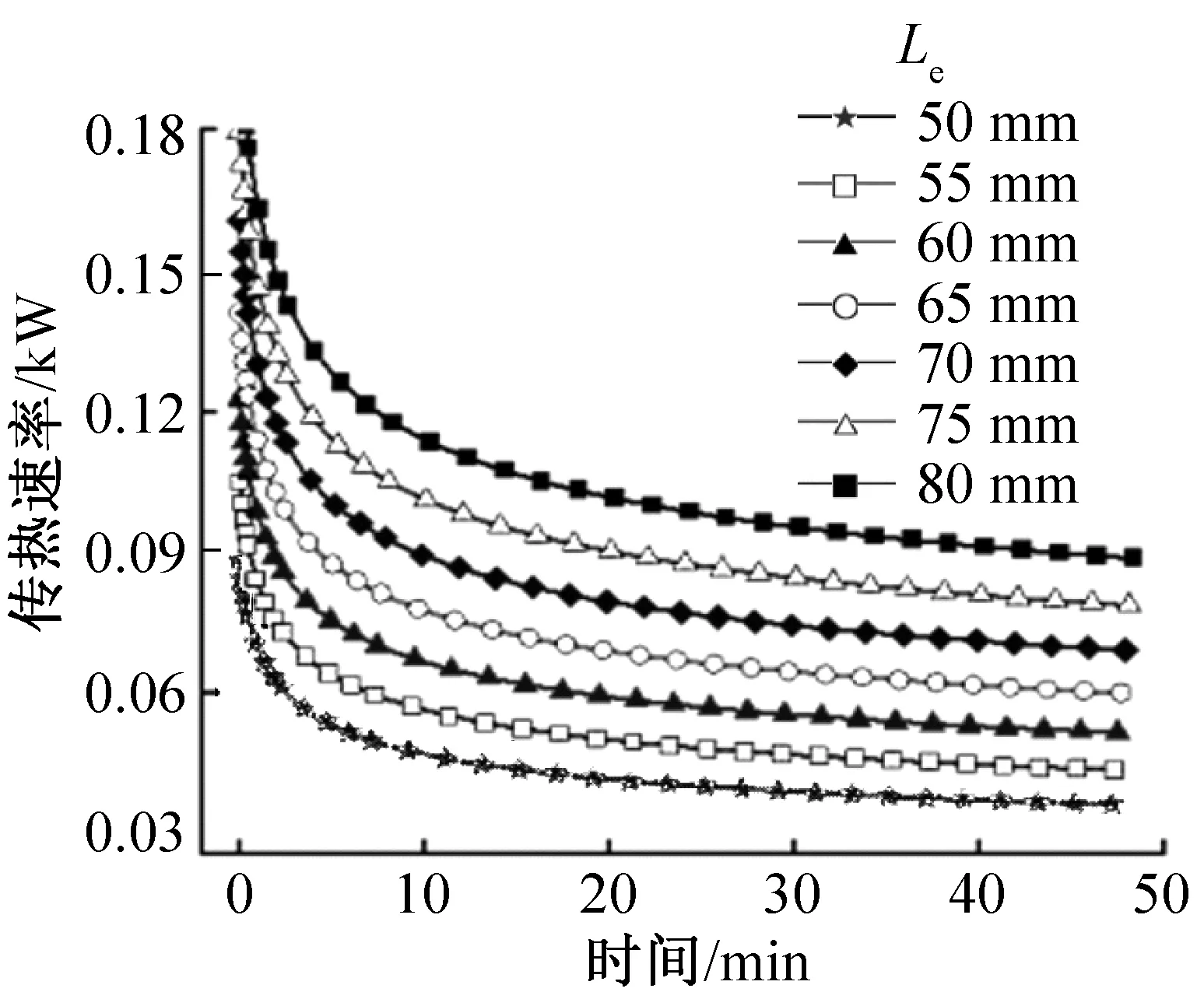
图6 热管蒸发段长度对瞬时传热速率的影响Fig.6 Effect of evaporation section length of heat pipes on the transient heat transfer rate
由图5可知,随着管排数和热管外径的增加,蓄冷板的瞬时传热速率增大,在管排数为4,管径为16 mm时,平均传热速率可达到88.72 W。同时,对于部分管排数少但外径大的情况,其瞬时传热速率与管排数多但管外径小的情况接近,如图5中,管排数为3、外径为16 mm与管排数为4、外径为8 mm时,两者的瞬时传热速率曲线接近,说明两者具有相似的传热性能。这可为热管嵌入式相变蓄冷板的设计提供参考依据。
图6所示为热管蒸发段长度对蓄冷板瞬时传热速率的影响。在模拟过程中,采用的热管管排数为3排,外径为12.7 mm,空气质量流量为0.096 kg/s,同时假设热管蒸发段的翅片面积随蒸发段长度呈比例变化。模拟结果表明,蓄冷板的瞬时传热速率随热管蒸发段长度的增加而增大,在蒸发段长度为80 mm时,平均传热速率可达到112.54 W。需说明的是,随着蒸发段及翅片传热面积的增加,保持空气侧质量流量不变使得空气侧的风速减小,但整体而言,瞬时传热速率仍随传热面积的增加而增大,这说明空气侧的传热面积在整个传热过程中为主导因素。
最后,由模拟参数可知,由于热管几何尺寸和管排数的影响,蓄冷板的内体积也会发生变化,进而影响相变材料的填充量,因此,针对图5中瞬时传热速率相近的情况,计算了相变材料的填充系数(除热管外的蓄冷板内体积除以蓄冷板内总体积),结果如表6所示。由表6可知,当考虑易于应用并获得相对较大的瞬时传热速率时,应选择热管管排数较少但管径较大的布置方式;相反,当考虑获得较大的填充系数且保持较高的传热速率时,应选择热管管排数多且管径较小的布置方式。

表6 相变材料的填充系数Tab.6 Filling factors of the phase change materials
4 结论
本文针对短途冷藏运输的轻量化用冷及用冷需求多变的问题,提出了热管嵌入式相变蓄冷板以快速平衡大温差负荷,实验研究了热管侧动态释冷过程,搭建了空气-热管-相变材料间的动态传热解析模型,实验验证了该模型的准确性,模拟分析了热管几何参数及排布对蓄冷板释冷性能的影响,得到结论如下:
1)实验测试了送风温度为30、40、50 ℃工况下蓄冷板热管侧的平均传热速率及进出风温差,在50 ℃工况下平均传热速率最大可达42.50 W,进出风温差动态变化显著。
2)模型以空气侧进口温度为输入参数,可计算得到相变材料内的液-固界面半径rpl,瞬态传热效率ε和空气侧出口温度Tout。模型计算的空气侧出口温度与实验测量值吻合,偏差最大为-0.52~1.19 ℃,总释冷量的计算误差分布在-3.21%~6.16%之间。
3)模拟分析结果显示,随着热管管排数增加、管外径增大以及蒸发段长度增加,蓄冷板的瞬时传热速率增大。在模拟算例中,管排数为4,管径为16 mm时,平均传热速率可达88.72 W,蒸发段长度为80 mm时,平均传热速率可达112.54 W。同时,部分管排数少但外径大的热管布置方式可以获得与管排数多但管径小的布置方式相接近的瞬时传热速率。根据不同布置方式下相变材料填充系数的计算结果,当考虑易于应用时,应选择热管管排数较少但管径较大的布置方式。当考虑获得较大的填充系数且保持较高的传热速率时,应选择热管管排数多且管径较小的布置方式。
本文受天津市自然科学基金(18JCQNJC77500,18JCQNJC77400)和天津市科技计划项目(20ZYCGSN00310)资助。(The project was supported by the Tianjin Natural Science Foundation (No.18JCQNJC77500 &No.18JCQNJC77400)and Tianjin Municipal Science and Technology Project (No.20ZYCGSN00310).)
