视觉系统中摄像机标定方法研究现状及展望

田俊英， 伍济钢， 赵前程

(湖南科技大学 机械设备健康维护湖南省重点实验室，湖南 湘潭 411201)

1 引 言

视觉是人类从外界环境中获取信息最主要的途径，以其效率高、功能强大、适用范围广等优点被广泛应用于工业检测、医学图像分析和农产品品质检测及分类等诸多领域[1-2]。1977年，英国教授Marr提出的Marr视觉理论中认为：一个完整的双目立体视觉系统主要包括图像采集、摄像机标定、特征提取、立体匹配以及三维重建这5个方面[3-4]。摄像机标定作为立体视觉测量的基础[5]，对后续立体匹配的成功率和三维重建的准确度有直接影响，因而找到一种高效便捷的标定方法尤为重要。

所谓摄像机标定，就是根据摄像机成像几何模型，利用已知特征点的三维空间物体位置与二维图像坐标的映射关系，求解摄像机成像的基本参数以及摄像机对于世界坐标系的方位[6-7]。摄像机标定技术最早是应用于摄影测量学[8-11]，通过数学解析的方法建立联系来标定相机。但由于机器视觉与一般摄影测量的使用要求、应用场合等方面存在差异，人们必须研究出更加适合机器视觉系统的摄像机标定方法，通常，根据标定目标的空间维度可分为4类[12]：基于三维物体的标定[13]、基于二维平面的标定[14]、基于一维分段的标定[15]和零维自标定[16]方法，同时通过比较各标定方法操作的智能性、标定过程的实时性、标定结果的准确性、对标定环境的抗干扰性等关键技术指标体现标定方法的优势及适用范围，并以此来评价标定方法。针对视觉系统对标定技术的高要求，人们也不断改进算法来提高标定效果。

本文首先对视觉系统的发展现状与整体流程进行简要介绍，突出了摄像机标定在整个过程中的重要性；其次提出摄像机标定方法可根据标定目标的空间维度分为4大类，基于各类标定方法存在的问题论述了研究人员对该方面的改进与其发展现状，并对各种改进方法的特点进行比较；最后总结了当前各类标定方法存在的优势与不足，并对以后摄像机标定技术的发展趋势做出预测。

2 三维标定法

三维标定法以固定在平面板的多个立方体为标定靶标，将其放在多相机视觉测量系统的工作范围内，通过硬件控制触发多相机同步采集立体靶标的图像，利用图像信息标定出每个相机的内外参数。但三维标定物普遍存在定制复杂、价格偏高等问题。

根据对近年来该方面文献的研究，我们找出了基础的三维标定方法，并按存在形态将其分为两大类：第一类是使用3D实物立体靶标实现三维标定[17-18]，并对靶标的不同结构分别展开研究；第二类是通过构建虚拟立体靶标实现相机三维标定[19]。

2.1 基于实物立体靶标的标定

2.1.1 球体靶标

球体标定以球形物体作为标定对象(图1)，利用球体图像二次曲线的性质，即使在发生遮挡等问题时也能够恢复轮廓。该方法通过拍摄不同角度的球体图像，将得到的二次曲线进行提取匹配，并根据约束条件实现基于球体的三维标定。

图1 立体靶标图[17]Fig.1 Stereogram[17]

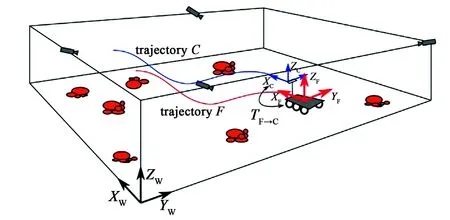
图2 运动捕捉系统[30]Fig.2 Motion capture system[30]

三维标定法最早出现于1986～1987年，根据曲面中各点与成像平面距离不同，Roger和Tsai等[20-21]提出将单视图共面点沿z方向移动不同的高度，构建非共面点并利用径向一致约束(RAC)条件标定3D摄像机，可用于精密的测量，为以后3D标定物的制作与使用奠定了基础，但靶标制作难度较大，特征点提取困难。为降低靶标制作成本，1994年Daucher等[22]基于四点双报表对齐、投影不变量原理，使用一个球体在多个位置的图像确定相机内参数。此后球体靶标应用起来，该方法对部分失真问题不敏感，但误差较大。Teramoto等[23]不满足于单个球体的应用，取3个球的单幅图像，使用Levenberg-MarQuardt算法对球体靶标进行二次曲线到绝对二次曲线的转换，从每个球的边界点最优地估计摄像机内参数。Ying等[24]则利用几何不变量原理推导相机内参数的约束方程，对比得出多个球面投影的方法比直线投影具有更好的鲁棒性和精度。陈刚等[25]在Roger和Tsai等的非共面点方法基础上，设计了一种真实的非共面标定模板直接通过多个球体获得特征点，提高了双目视觉系统的标定效率。而赵成运等[17]通过多个球体共面的模板，将球心作为角点数据标定，结果在角度变化较大时，标定精度和稳定性更好。Ying和Zhang等[26-27]利用绝对二次曲线与球面图像的各理论关系，用多个球体标定摄像机内参，有效缓解了分步累积误差和额外参数导致的精度低的问题。Wong等[28]则利用绝对对偶二次曲线与球面分层理论进行了内、外参数全标定，通过两个球面的双切包络获得的2个附加特征点和3个球面的核线切线来恢复视差。Su等[29]用一种球面拟合算法识别彩色图像和深度图像中球心的运动位置，使用外部网络标定方法建立视图对应完成了摄像机外部参数标定。至此球体靶标已实现了大部分标定功能，但三维空间度量结构的畸变效应在实际应用中仍未解决。Chiodini等[30]基于解决相机切除问题来计算相机相对于一组球面逆反射标记的姿态，利用图2所示的具有跟踪摄像机并提供轨迹地面真相能力的运动捕捉系统测量球面逆反射标记物的三维坐标，计算相机相对位置和方向。由于不受任何附加的视觉标定目标装配的系统误差的影响，极大提高了标定精度。基于球体靶标的相机标定方法发展至今已经得到了很大的提高，尤其是在标定精度方面能够达到1 mm的位置精度和优于1°的定向精度。标定精度一般可以通过重投影误差来表示，其重投影误差可以达到0.7 pixel。球体靶标具有较强的抗遮挡能力，但其制作成本较大，且边缘检测精度较低使得特征点提取困难，因此要提高球体靶标的特征点检测的精度。

2.1.2 其他立体靶标

除了球体可作为标定目标外，许多研究人员也考虑使用一些制作与结构更简单的立方体来标定相机。多面立体靶标以立方体为标定对象(图3)，通过识别不同侧面附着的特征图案进行标定，其中向量eo指向附着特征图案的表面，θ为四棱锥的二面角，即附着特征图像的两个相对面正方向的夹角。用多相机系统同步采集多面立体靶标图像，在4个侧面分别建立不同的平面坐标系，然后提取出图像上特征圆圆心的像素坐标，利用特征圆的靶面坐标系中的实际坐标实现多相机标定[18]。

(a)结构图(a) Atructural drawings

(b)实物图(b) Physical drawings图3 多面立体靶标[18]Fig.3 Polyhedral target[18]

1994年，Healey等[31]最初根据立体靶标曲面片的图像估计场景变化，将相机噪声引起的图像方差与场景效应引起的方差分离，完成相机标定；雷彦章等[32]利用光栅投影在三维形貌上的高度差标定相机，通过单目测量结果来补充双目测量中的空缺部分，首次结合了单、双目标定方法，改善了测量范围与结果的完整性；对于相机内参可变的情况，Sturm[33]和祝海江等[34]分别使用3个相同的棋盘格与圆形平面模板互相垂直构成的3D半包围结构，并考虑径向畸变参数与特征点的反投影误差等进行相机标定，弥补了2D模板无法覆盖整个鱼眼图像的缺陷；孙军华[35]和刘震等[36]也利用组合棋盘格的方法，以子靶标之间相对位置不变为约束条件，建立重投影误差最小的目标函数标定摄像机，可根据视场范围调节小靶标距离，具有灵活、高效、制作简单等特点，解决了大视场标定中靶标加工困难和精度低的问题；Huang等[37]则设计了侧面附有棋盘格的封闭正方体模板，令每个摄像机只在一个侧面上校准，最后统一于世界坐标系，实现了多个摄像机的全局同步标定，解决了单摄像机测量信息不全的问题；余寰等[18]用圆形平面模板与编码图案组合成正四棱锥立方体，仅需两相机同时拍摄靶标图片就能标定两相机内外参数，提高了多摄相机标定的精度与自动化程度。该种标定方法目前能达到的最好精度效果是误差范围约为-0.2～0. 2 pixel，大多数点在-0.1～0.1 pixel范围内。多面立体靶标能够更加准确地实现多相机的同步标定，但多个平面坐标系进行统一时计算量较大，对于靶标的制作精度要求也较高，能否使用智能化手段准确地完成计算是未来要进行研究的重要方向。

2.2 虚拟立体靶标

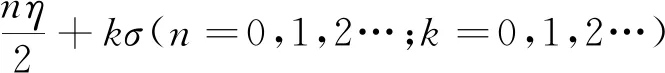
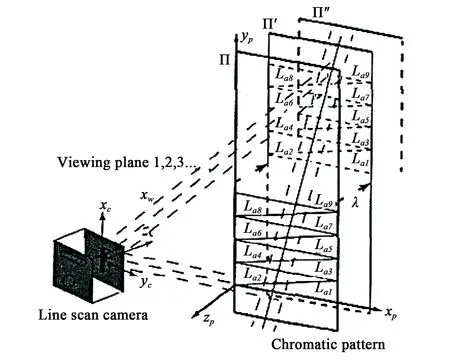
(a)虚拟立体靶标构建过程(a) Virtual stereo target construction process diagram

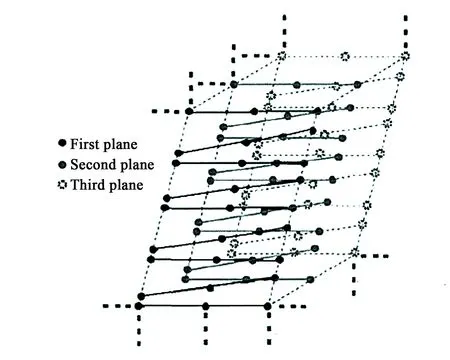
(b)虚拟立体靶标示例图(b) Illustration of a virtual stereo target图4 虚拟立体靶标[19]Fig.4 Virtual stereo target[19]

2005年，Svoboda[38]与杨博文等[39]通过在相机范围内多次移动亮点构建虚拟立体靶标，完成虚拟沉浸式环境多摄像机系统的标定，解决了大视场标定时只能覆盖一小部分标定空间的问题。Shen等[40]用内视视觉传感器网络(VSN)模拟器设计了一种中心是大球体，周围环绕几个刚性安装的小球体的靶标，通过绕中心轴旋转更改外部球体位置的结构特点来提取外部参数，简化了标定过程。王子辰等[19]利用平面靶标与相机多次曝光构建虚拟立体靶标，根据亚像素精度像点与特征点空间位置的对应关系建立多特征超定方程，用最小二乘法迭代求解相机参数，解决了线阵摄像机标定时特征点选取与控制的问题，可通用于类似线性探测器的标定方法。目前标定效果较为理想的是平均标定精度达0.26 pixel。虚拟立体靶标能更加方便对特征点的控制，也可以适用于多种场景的标定，但立体靶标的结构构建比较复杂，对于靶标的呈现效果也要经过诸多试验。

3 二维标定法

二维标定法是通过对二维标定板进行多角度拍摄，然后识别特征点，建立单应矩阵，求解线性系统并进行优化，由此得到相机的内外参数。二维标定法由于其灵活性和易操作性，是当前相机视觉系统中应用最广泛的标定方法，但其对于控制点数量和匹配精度等方面的不足亟待解决。

随着对视觉系统标定的研究不断深入，可以将现有的二维标定法按照标定模板的原理分为两大类：一是以方形图案为平面标定模板，其中最具代表性的要数张正友的棋盘格标定模板[14]；二是以具有二次曲线性质的共面圆等图案[13]为模板标定相机。

3.1 基于二维方格的标定

在二维标定中，将方格均匀排列作为标定模板。图5为方形平面模板类型，选取方形图案的角点作为特征点标定。拍摄模板图案并识别角点作为特征点，根据特征点对应关系与图像约束条件实现相机标定。

(a)Letraset速刻图板(a) Letraset stencils

(b)棋盘格图案(b) Checkerboard

(c)格雷码图案(c) Grama图5 方形标定模板Fig.5 Square calibration template

二维标定模板最初是通过检测正方形的角点来实现。二维标定法最早出现于1981年，Martins等[41]基于两个标定平面的数据对摄像机模型进行了研究，相机标定提供了图像平面中的点相对应的空间中的视线光线所需的模型参数值，为摄像机二维标定奠定了基础。Horaud等[42-43]借助精密位移平台移动平面模板，单扫描线性摄像机的标定法，并在后续修改中增加了畸变影响，通过非线性优化来求解参数，使该标定方法更加实用。Tsai等[21]首先提出用包含16个黑色正方形的金属块顶面作为平面模板，通过单视图的二值化图像轮廓来检测矩形标定图案的角点。Trucco等[44]采用白色背景上有两个深色矩形的平面网格，将图像进行边缘检测处理，使用Hought和直线交点来定位角点。Mei等[45]也利用平面网格标定全方位单视点相机，采用一种识别良好的函数来模拟真实误差，解决了镜头失真等误差导致的最小化问题，验证了对鱼眼与球形相机的有效性。Zhang等[46]提出用相机拍摄至少2个不同方向上显示的棋盘格图案，考虑径向畸变并基于最大似然准则进行非线性优化标定摄像机，更加灵活、简单，棋盘格在速刻图板的基础上增加了深色图案的占比，更加清晰地将两种背景图案划分开，相比速刻图板能够得到更加精确的角点检测结果。此后棋盘格图案开始盛行。Zhang等[14]从不同的角度拍摄至少3幅棋盘格模板图案，提取角点坐标并与单应性矩阵建立方程组，线性分解来实现摄像机参数标定，作为最经典的一种方法，标定精度相对较好，适用于非实时标定。Scarmuzza等[47]在黑白棋盘格的基础上，采用泰勒级数展开的方法描述图像的投影函数。与经典方法比较，该方法独立于传感器，使用更加灵活方便，适用于不同类型的全向视觉系统。后又有人重新制定非线性最小二乘优化方法，并应用允许联合优化所有标定参数的残差函数，提高了系统性能，简化了标定过程。Draréni等[48]通过获取不同方向的棋盘格图像，利用图像诱导的单应关系和一种线性算法来标定线性摄像机的内外参数。卜鹏辉等[49]在棋盘格模板左下角处添加了一个圆形标志点，通过重投影误差最小实现单个摄像机标定。由于亚像素级角点坐标的排序不随棋盘格摆放位置而变化，极大提高了标定的自动化程度。赵亚凤等[50]在棋盘格的基础上提出利用两对正交消隐点，计算相机主点和归一化焦距，作为内参数的初值，再利用优化的差分进化算法进行全局寻优，完成相机畸变校正，最后根据优化后的消隐点坐标求得双目相机的旋转矩阵和平移向量。该标定算法具有稳定可靠、精度高、抗干扰能力强的优点。He等[51]结合K-SVD稀疏字典学习与棋盘格图像构造稀疏字典，并及时更新相机变化，实现高精度、高效率的相机标定，详细过程如图6所示。Sels等[52]使用LCD屏幕上显示的格雷码图案代替棋盘图案，通过格雷码图案解码LCD屏幕上点的3D信息。在对CMOS相机的标定中，格雷码相比于棋盘格模板，图案简单并且能够直接通过解码来实现信息的提取，在转化过程中也可以避免错误数码的产生，使得标定算法更加稳定，精度更高。对比同等情况下的各类标定方法，效果较好时重投影误差可低至0.15 pixel左右，能够得到较好的标定精度。作为最常用的标定方法，在倾斜角度较大时标定精度急速降低，对于倾斜时的角点检测算法需要进一步提高。

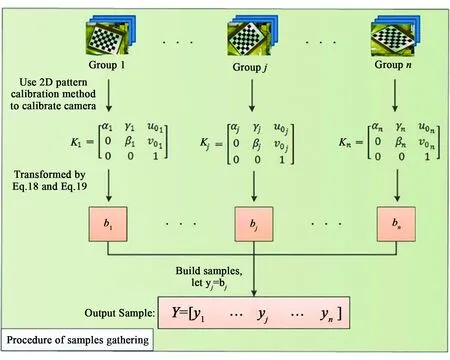
图6 标定矢量提取过程[53]Fig.6 Calibration vector extraction process[53]

3.2 基于二次曲线的标定

正方形、棋盘格等图案的标定法对标定相机角度变化限制较大，角度过大时角点误差会增大，角度过小时标定模型易退化。为了解决此类问题，提高标定精度，共面圆、同心圆等二次曲线性质的圆形图案(图7)逐渐得到应用。该方法以圆形图案作为平面标定模板，通过投影具有二次曲线性质的圆形图案，更加精确地定位中心并将其作为特征点，结合其他约束条件标定相机。

(a)共面圆(a) Coplanar circles

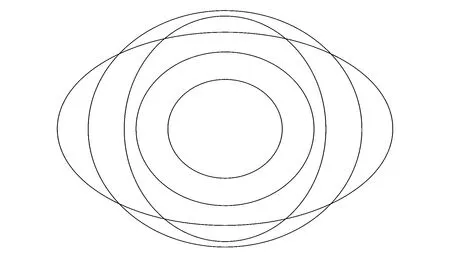
(b)同心圆(b) Concentric circles

(c)相交圆(c) Intersecting circles图7 圆形标定模板Fig.7 Circular calibration template

1997年，Heikkila等[53]考虑圆形特征作为标定目标，通过定位特征质心来反复修正透视效果。而后针对实时标定不易实现的问题，又提出一种非递归的失真模型反演方法[12]，标定模板以圆孔中心为参照点，进行非对称性投影来对圆孔投影校正，实现了对精密3D视觉系统摄像机的实时标定。Mateos[54]和Kang等[55]分别使用连通分量标记算法、积分图像法对圆形标定板图像进行亚像素特征定位匹配，实现了亚像素精度，提高了鲁棒性，并有效解决了工业应用标定中光照不均、背景杂乱及图像质量较差等问题。单宝华等[56]使用Canny-Zernike组合算法实现圆形标定模板圆心坐标亚像素定位，以三角形标记的圆心排序法和靶标对角线上圆心距离为约束条件标定立体系统，有较好的精度和自动化程度。Wang等[57]提出圆形标定模板下运用帕斯卡定理，通过牛顿迭代法求解圆点图像，再将绝对二次曲线约束转化为帕斯卡线约束来标定摄像机内参，扩大了标定的应用范围。孙楠等[58]则用两根带有圆形编码元的靶尺构建十字形平面靶标，双相机拍摄靶标一次，再分别单独拍摄多次，采用多视图几何约束获得相机内参，根据各自靶点对应点集计算双目视觉系统外部参数，实现大视场的标定。杨长江[59]和Zhu等[60]提出使用3个同心二次曲线的平面模板，摄像机拍摄背面等不同方位的图案，即可直接求解参数，简化了基元的对应问题。孟晓桥等[61-62]基于经典棋盘标定法要求摄像机在3个不同方位拍摄一个含有若干条直径的圆图像，线性求解全部摄像机内参数，整个过程不需要建立模型点与图像点的对应关系就能自动完成标定，适合非视觉专业人员使用。 Xu等[63]提出用两个相交的共面圆作为标定模板，利用射影平面上关于交点的两个相交圆的理论和一个核线几何来求解圆点图像，通过同一图案不同方向的3幅图像中的圆点图像线性确定内参数。Chen等[64]使用计算机模拟的随机散斑图案作为标定目标，结合最先进的数字图像相关(DIC)算法对标定目标的控制点与捕获的校准图像上的对应点精确匹配，实现了相机内外参数的精确提取，在高精度光学计量、高精度和有效的透镜偏转校正等方面具有很大的潜力。针对无干扰的模拟实验与有噪音干扰的真实实验情况，得到其重投影误差分别为0.004 pixel和0.038 pixel，标定精度有了极大程度的提升。该方法在有干扰的环境中依然具有较高的标定精度，得到了研究人员的极大关注，对其标定图案的选择也较为成熟，可以进一步利用一些合适的算法提高标定速度。

(a)捕捉的一组标定图像(a) A set of calibration images captured

(b)标定目标的姿态(b) Poses of the calibration target图8 标定参数可视化[64]Fig.8 Visualization of calibration parameters[64]

4 一维标定法

一维标定法是通过控制一维标定杆绕一个定点旋转，根据标定杆在运动前后所在平面和像平面的单应矩阵推导摄像机的内外参数信息。一维标定物制作简单、使用范围广，但该方法要求标定物做受约束的运动，降低了标定结果的稳定性和准确性。

根据现有的一维标定方法，我们将它们大致总结为两大类：一是依据单个1D标定杆完成标定的方法，它主要包括最基础绕点旋转和一般运动两种形式；二是多个1D标定物组合来实现相机标定。

4.1 基于单个标定杆的方法

4.1.1 绕点旋转

一维标定法是基于绝对二次曲线图像的代数约束，以一根尺寸已知的1D标定杆作为标定物，指定空间一点作为旋转中心(图9)，在旋转时拍摄多幅图像，根据标定杆上多个特征点的对应信息建立约束方程，实现一维标定。

一维标定法最早提出于2004年，Zhang等[15]控制1D标定杆绕一定点旋转拍摄至少6幅图像，要求标定杆运动前后处于同一平面，根据图像点间的对应关系与标定物的几何信息求解相机参数，填补了标定方法在该维度的空缺。Wu等[12]将1D标定杆的旋转标定扩展到2D平面标定，标定杆绕点旋转等效于平面，当标定杆作平面运动时该理论仍成立，但无法用传统方法处理。针对Zhang等[15]的方法仅用于估计内部参数，且标定时未考虑相机失真的影响，He等[65]提出以线形标定对象为基础，对包含畸变参数在内的内、外参数进行了多层摄像机标定。França等[66]分析Zhang等[15]的原始方法并重新表述问题，提出基于分区Levenberg-MarQuardt算法的归一化非线性求解方法，充分利用标定问题的特殊结构，降低了原方法的计算复杂度，提高了计算精度。Shi等[67]引入对图像相似性变换具有不变性的估计器，利用不同图像估计的相对深度的标准差的倒数作为相似不变线性校正算法约束方程的权值，精度略高于归一化线性校正算法。史坤峰等[68]在Shi[67]的基础上，将相对深度约束方程与绝对二次曲线方程组进行最优加权，既保留了标定精度，也简化了算法。Wang等[69-70]利用数据归一化提高1D标定物上标记点相对深度的估计精度，通过分析约束中涉及的数据误差，自适应地为每个约束分配一个加权系数，标定精度远高于经典一维标定法。此后又提出用凸松弛法求出每个摄像机中绝对二次曲线的最优解和内参，利用矩阵运算计算多摄像机系统的外参数，既提高了精度又加快了收敛速度。Hammarstedt等[71]基于一维标定法的退化情况，给出了1D标定物的临界运动，证明了对固有参数的约束使得闭合解简化、临界运动集减少。Zhao等[72]针对绕定点旋转的1D标定物，将秩分解与拉普拉斯方法相结合，通过尺度测量矩阵的因式分解，用解析方程估计投影深度，恢复多摄像机系统的内外参数。Ma等[73]参考现有的一维标定法，提出标定杆绕中点而非端点旋转时，其端点轨迹为圆，利用圆点与绝对二次曲线的关系和正交性约束来标定摄像机参数。吕耀文等[74-75]将一维标定对象定位于世界坐标系的X轴上，首先提出使用标定杆之外的空间点，利用坐标系原点作为旋转固定点，定义标定点与对应像点之间的1D单应矩阵，在图10中叠加6个标记点在50幅图像中的投影图像点，从单幅视图推导基本约束方程，采用线性最小二乘与反投影误差最小的目标函数估计摄像机初值。Qi等[76]则扩展了适用于标定的运动模式，有多个标记的1D标定物只受重力作用，绕着一个在平面上移动的标记旋转，打破了只能绕固定点标定的局限，由此给出了摄像机内部参数的约束方程。使用标定结果与设定真值的相对误差作为标定精度的评价标准时，标定的相对误差一般稳定在0.2%。对于标定杆中定点的选择，可以有针对性地根据不同的标定场景做出改变，以扩大实用性。

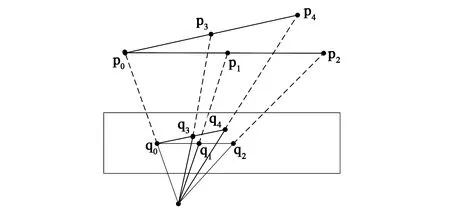
(a)绕端点(a) Around the endpoint

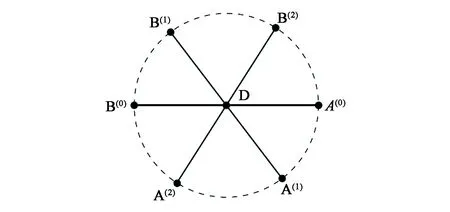
(b)绕中点(b) Around the midpoint图9 绕点旋转的一维标定Fig.9 One-dimensional calibration of rotation around a point

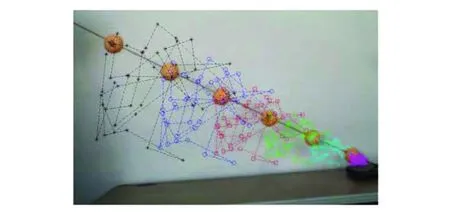
图10 叠加6个标记点的1D标定杆[74]Fig.10 1D scale bar with 6 markers superimposed[74]

4.1.2 一般运动

在绕点旋转的标定方法中，对于点的选择与稳定性的保持等问题都会产生不同程度的误差。为了减少对标定杆的约束，人们开始考虑在一般运动情况下(图11)的一维标定。同样以1D标定杆作为标定物，但是对于标定杆的运动不做限制，进行多次任意刚体运动，结合特征点与约束条件进行标定。

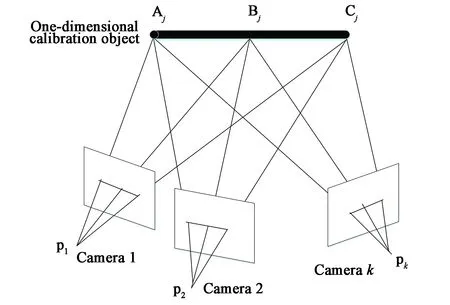
图11 一般运动下的一维标定Fig.11 One-dimensional calibration in general motion

2007年，Qi等[77]以抛掷一维物体的特殊动作证明了一般运动是一维标定有解的充要条件，在此基础上，通过避免奇异性，提高了方法的精度和鲁棒性，超过了同类方法。王亮等[78]对作任意刚体运动1D标定物，使用最大似然准则与线性算法标定多摄像机系统，既解决了2D与3D标定物遮挡的问题，也提高了一维标定法的精度。邓小明等[79]认为如果1D标定物包含至少5个共线点，则标定物进行至少3次的刚体运动即可标定反射折射摄像机，通过计算消隐点求解内参数矩阵，但径向畸变会存在一定误差。付强、França和付仲良等[80-82]提出1D标定物作自由运动，采用从投影空间转换为欧式空间的方法，利用基本矩阵与特征点距离的约束，完成双目标定，继而完成多摄像机系统标定，解决了基于消隐点的一维标定算法抗噪声能力差和在抑制径向畸变的缺陷。王波等[83]总结现有一维标定法的研究，证明从单应矩阵的角度也可以得到摄像机内参数的相关约束，不仅限于标定杆绕定点转动，同样适用标定杆在平面内自由运动的情况。在现有条件下，该类方法在估计内在和外在相机参数中获得的误差约为0.5%。作为应用范围较广泛的一种标定方法，能适应多种场景，但标定精度较低，应探究更便捷的方法进行标定杆运动参数的计算。

4.2 基于组合标定杆的方法

联系标定杆与标定平面之间的关系，人们提出基于二维标定原理组合多个1D标定杆(如图12)来标定相机。以不同形式组合的标定物作为标定模板，相机拍摄多幅图像，对标定物的特征点匹配计算，根据约束条件实现标定。

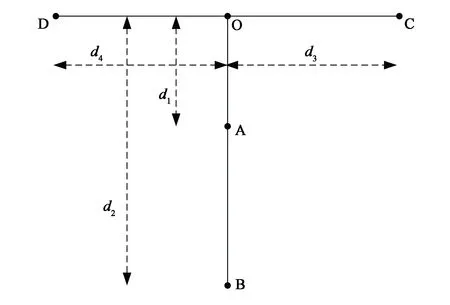
图12 组合标定杆原理图Fig.12 Schematic diagram of combined calibration bar

2010年，Miyagawa等[84]提出仅根据两个正交的1D标定物上的5个点估计相机参数，每个物体有3个共线点，一个是共享的，利用束平差技术优化参数，用两幅1D标定物构建了2D平面模板，将两者联系了起来。薛俊鹏等[85]就Miyagawa[84]提出方法有更详细的解释，利用两个正交1D标定物构成“T”型靶标，根据柔性靶标原理计算共线的4点，由射影变换同素性、接合性以及交比不变性标定镜头畸变并进行畸变校正，通过坐标变换标定相机。杨珍等[86]提出取消对两个标定物的放置要求，任意放置在摄像机视场内，通过双1D靶标的消隐点和空间夹角所成角度恒定这一约束求解大视场摄像机内参数，减少了靶标之间的约束。该方法可以达到的最好标定效果是重投影误差为0.313 pixel。虽然标定精度较好，但标定目标不够灵活，难以实现在较小场景中的应用。

5 零维自标定

零维自标定是指不需要任何标定块，仅通过图像点之间的对应关系就可以求出摄像机的内外参数。该方法不需要任何标定目标使标定过程更加灵活、方便，但由于其复杂的数学运算，导致该方法精度不高、鲁棒性不足。

自标定方法[87-89]以其应用范围广、无标定无限制的优势得到了国内外研究人员的极大关注，涌现出许多高精度、高效率的自标定方法。我们根据了标定原理将其分为3类：一是基于绝对二次曲线和外极线变换性质的自标定[89-94]；二是基于主动视觉理论的自标定[95-99]；三是基于分层重构方法的标定[100-107]与改进。

5.1 基于绝对二次曲线与外极线变换性质的标定

自标定方法最初是根据绝对二次曲线和外极线变换性质来实现的。通过相机移动过程中的极线变换，结合场景的约束条件来标定相机。

1992年，Hartley、Faugeras和Maybank等[87-89]首次提出摄像机自标定的思想，相机发生位移时的极线变换施加了两个代数约束，使得曲线参数化。如果有3个核线变换，则可以在对偶平面上得到两条六次曲线，通过两条曲线有一个共同的三阶奇异点求解Kruppa方程得到正确的摄像机标定。Zeller等[90]基于Maybank等[89]的算法，增加了一些经典的视频序列处理技术，如图13中的特征提取和令牌跟踪，使得从视频序列计算观测场景的三维尺寸成为可能。Luong等[91]通过绝对二次曲线将固有参数和基本矩阵联系起来，使用未校准的移动摄像机和定义一个投影摄像机来标定静态场景。该种标定方法下的给定图像坐标和测量值间像素差为0.26 ～ 0.33 pixel，标定误差大约为5% ～ 10%。当前由于复杂的计算过程，对于该标定方法的研究也逐渐开始转向更加便捷、智能化的方向。

(a)不同位置场景图(a) Different location scenarios

(b)特征提取(b) Feature extraction

(c)特征重建(c) Character reconstruction

(d)重建后的视图(d) Reconstructed view图13 根据视频序列的自标定流程[90]Fig.13 Self-calibration flow based on video sequence[90]

5.2 基于主动视觉系统的标定

绝对二次曲线与外极线的变换增加了运算难度，使相机标定精度较低。人们提出利用主动视觉系统平台控制相机做纯旋转或纯平移运动，根据运动过程中的运动序列求解相机参数。

图14 纯平移运动下的扩展焦点[92]Fig.14 Focus of expansion of a pure translation[92]

1996年，Ma等[92]利用主动视觉系统的灵活性，直接使用环境图像来标定摄像机，在摄像机内参数已知时，采用3次纯平移运动求解摄像机外参数；内部参数未知时，通过两组三正交平移组成的两个运动序列，确定内参数与部分外参数，并根据平台的任意非平移运动求解摄像机剩余外参数，如图14所示。杨长江等[93]在Ma[92]的基础上控制摄像机在同一平面作4组运动，其中每组包括两次相互正交的平移运动，同时适当调整摄像机平移运动的姿态，线性求解摄像机内参数。Agapito等[94]使用图像间单应作为输入，要求摄像机可以通过运动(自由旋转)或改变内部参数，但不能平移，基于可导致非线性最小化的无限单应约束，在扩展的图像序列上标定相机。Hartley等[95]则不改变相机位置，通过拍摄具有不同方向的多幅图像，对图像之间的点分析匹配来完成标定。与Maybank[89]利用图像核线结构自标定的结果有根本的不同，由于摄像机位置固定，因此确定点匹配不会出现遮挡、纵横比或照明变化的问题，适用于任意数量图像的非迭代校准算法。Faugeras等[96]也通过摄像机固定拍摄多幅图像来实现标定，对于一维图像，根据图像的三焦张量唯一确定一维投影相机两个内参数。对于二维图像，则需要对三焦张量进行线性估计，求出一元三次多项式的根，利用平面运动自标定二维摄像机。这类标定方法下的给定图像坐标和测量值间像素差范围是0.06 ～ 0.2 pixel，平均重建误差约为1 mm。但是对于标定控制台制作的成本较大且移动时要求精确，该类方法的应用已经在逐渐减少。

5.3 基于分层重构的标定及其修正

利用分层重构的方法标定相机也引起了少部分人的重视。它不要求摄像机作特定运动，只需要在任意场景中拍摄多幅不同的图片即可进行重建。同时引入约束确定搜索范围来完成相机标定。后为解决分层算法稳定性差的问题，提出引入二次曲面方法。

1999年，Hartley等[97]将获得的投影重建施加手性约束将其依次细化为仿射，进一步细化为欧几里得(或度量)重建。对于假设的平面在无穷远处的每个位置，归结为非平移摄像机的标定问题；Li等[98]利用视图之间的已知旋转角和摄像机的正方形像素识别投影框架中无限远的平面，获得摄像机的标定矩阵和实现度量重建。Elamsy等[99]利用每个变焦相机主平面的主要平移位移来估计平面在无穷远处的位置，相机主平面被编码在相应的透视投影矩阵中，在零偏斜和已知纵横比的假设下线性计算静止非旋转变焦相机参数。Cipolla等[100]利用场景中存在的强约束来构造三维模型，通过3个及以上正交方向的奇异点生成新的视点图像。在弧形结构环境中，使用平行和正交的约束条件恢复投影矩阵来标定摄像机的内外参数。霍炬等[101]同样利用正交的两组平行直线形成的消隐点的几何特性，拍摄4个位置的不同图像，建立内参数约束方程。求解内参数作为初值后，通过非线性法标定畸变参数建立消隐点坐标系求解摄像机外参数。Zhao等[102]根据中心投影的单应矩阵，推导出平面点阵的特征点坐标、对应的像点坐标、内参数、相对姿态之间的严格解析关系。拍摄至少3张照片，利用单应矩阵在两组正交方向上求解消失点，线性求解相机内参数，具有较高的精度和鲁棒性。洪洋等[103]在任意两个位置下拍摄两组正交平行线，获取两幅图像上共4个消隐点后，利用对应消隐点之间的无穷单应关系，结合正交消隐点与摄像机光心连线的正交性建立约束方程，对摄像机内参数稳定求解。Pollefeys等[104]提出从未标定的变焦/聚焦摄像机获得的图像序列中恢复度量重建，放弃了对相机与场景约束条件的利用，证明了像面无偏斜时可进行自标定，给出了自校准的最小序列长度，并提出了一种检测关键运动序列的方法。图15即为标定实验图。Kang等[105]根据折反射成像的特点，组装了一个独立的系统来获取长序列的全方位图像，仅通过序列中成对跟踪点特征的一致性来标定抛物折反射相机。该类方法在模拟实验中标定的误差幅值小于0.01 pixel，均方差小于0.13 pixel；在真实实验中的误差稍大，但整体精度仍然满足工业中的一般需求。为满足更高的精度要求，研究人员开始从正交消隐点入手，并结合一些简单的平面标定图案来实现相机标定。

(a)圆周运动序列的3幅图(a) Three images of a circular motion sequence

(b)俯视图(b) Top view

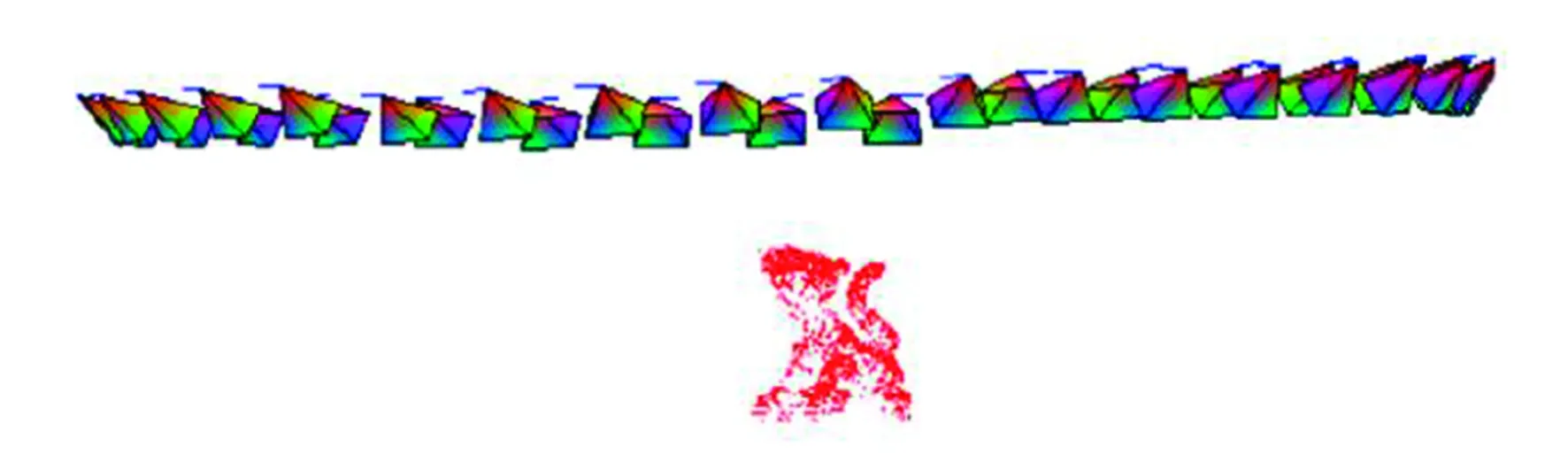
(c)侧视图(c) Side view

(d)重建后的不同视图(d) Different views after reconstruction图15 圆周运动分层自标定中结构与运动的重建[104]Fig.15 Reconstruction of structure and motion in layered self calibration of circular motion[104]

为解决分层算法的稳定性差等问题，Heyden[106]首次将对偶绝对二次曲面用于摄像机自标定。该方法得到的方程形式简单，能够避免由于分层算法引起的不稳定问题。Jin等[107]提出一种基于抽象二次曲面的摄像机自标定方法，该方法计算简单，鲁棒性好。通过对分层重构方法进行修正，得到的标定效果有所改进，不仅提高了稳定性还使得相对误差均小于0.02 pixel。

6 各摄像机标定方法的性能分析及比较

通过本文介绍，我们掌握了一些摄像机标定方法的分类与基础知识，表1给出了上述各摄像机标定方法的性能分析与比较。

相比于一维、二维标定法，三维标定法可更加灵活、便捷地实现多相机同时标定，球体投影的抗遮挡能力较强，标定精度和效率也相对较高。但由于立体靶标的制作困难，标定时需要昂贵的设备，标定过程中立体靶标特征点的三维坐标必须已知，一些立体靶标在标定过程中也会受到一定程度的遮挡，从而影响标定精度。

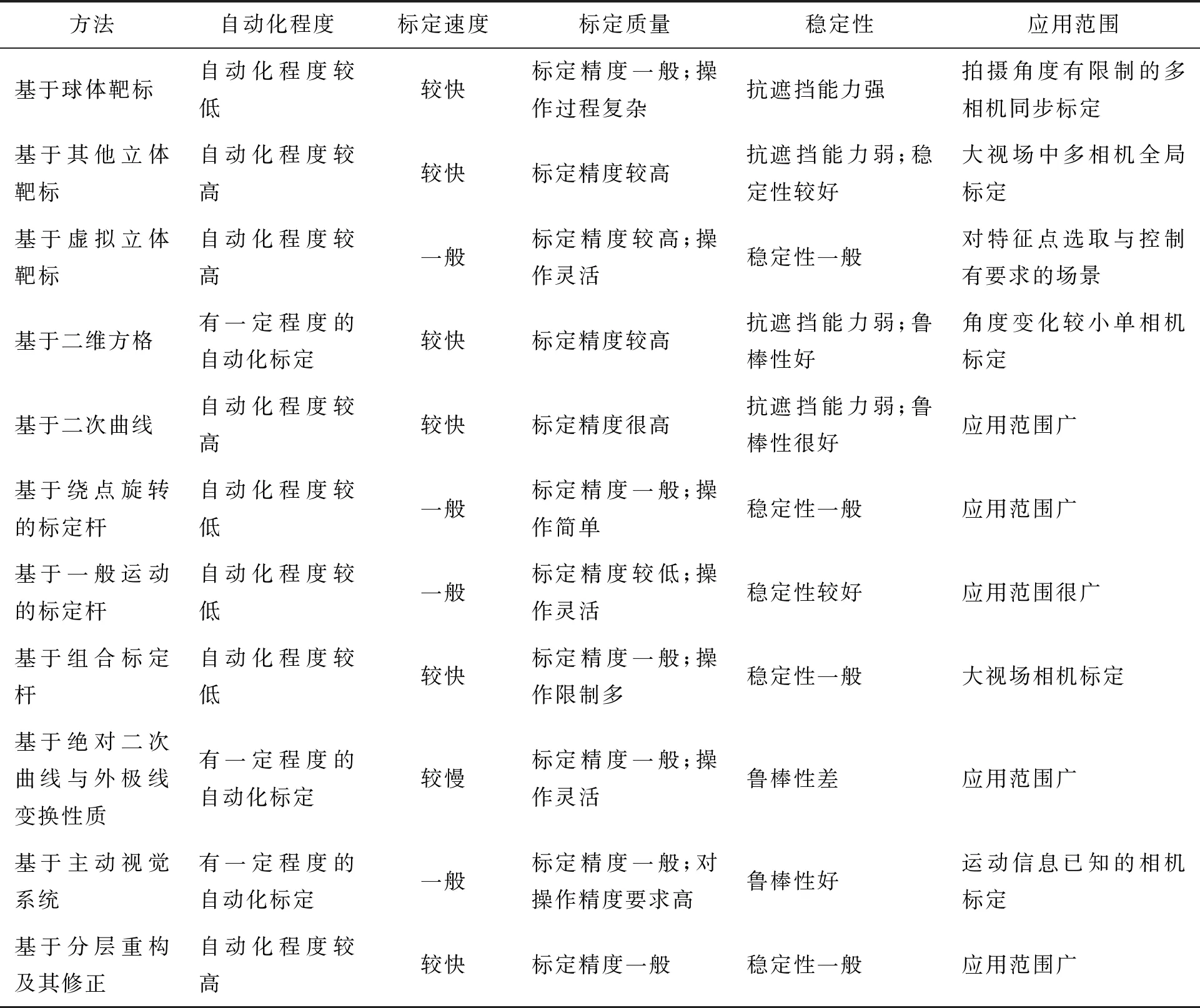
表1 摄像机标定方法对比及分析Tab.1 Comparison and analysis of camera calibration methods

二维标定法平面标定板制作简单、特征点制作精度相对较高、标定过程中标定板的姿态没有限制，具有较好的灵活性、鲁棒性。但局限于标定单个相机的情况，在对多相机进行标定时，平面标定板上的特征点会出现不同程度的遮挡和模糊现象，且多次拍摄统一参数的过程会产生一定误差，最终影响标定结果的精度，而一维标定物则在很大程度上避免了这种现象。

一维标定方法只需要将一维刚体放在摄像机可见范围内就能进行标定，同二维、三维标定目标比较，配置简单且在多相机系统中不存在遮挡的问题。一维标定目标在摄像机范围内运动时，如何保证在同一平面运动的问题也需要解决，由于其特征较少，所得到的标定精度也相对较差。

零维自标定不需要任何形式的标定块，仅依靠多幅图像之间的对应关系来建立数学联系来标定相机，具有很高的灵活性。但由于需要求解许多复杂方程，导致标定精度低、鲁棒性差、仅适用于部分精度要求不高的场合。

7 结 论

本文总结了摄像机标定的大致步骤和基本原理，按类分别研究了已有的标定方法，并对其突出方法进行了简单评价。总体而言，标定目标尺寸无论大小都有其各自的优缺点。

20世纪中后期开始出现摄像机标定方法的相关研究，发展至今在很多方面已经发展较为成熟，比如有一些方法在图片不够清晰的情况下也能进行标定，还有一些方法在标定过程中可以不受附加的标定目标装配的系统误差的影响等。但同时也存在一些问题，比如在复杂的场景中标定精度难以满足要求，某些在室外工作的设备，受到光线不稳定、干扰噪音大时标定精度提高困难；标定时在大量的角点提取与匹配过程中，运算量过大而导致标定速度较慢，无法达到实时标定的效果；标定的操作过程比较复杂，需要多次重复标定来减小人为操作误差，智能化程度不高；部分标定相机的平台与标定目标制作成本高，不具有普适性；摄像机标定应如何考虑畸变情况方面还存在较大缺陷等。在未来对摄像机标定方法的设计中，还是要以复杂环境下的高精度、高效率、高鲁棒性等的标定为主要研究内容，积极考虑相机畸变造成的误差，同时结合近年来快速发展的智能算法与各类应用软件提出有效的智能化标定方法实现相机全自动化标定，能够在一定程度上减少人为因素的干扰，也降低了标定过程的操作难度，智能算法的广泛应用使得价格昂贵、操作复杂、体积笨重的标定平台应用减少，这将进一步提高标定精度，降低标定成本，扩大适用范围，加强实用性。