聚合物稳定蓝相液晶器件的模拟计算模型
2021-12-16胡春鑫贾孟晓马红梅孙玉宝
张 波, 胡春鑫, 贾孟晓, 马红梅, 孙玉宝
(河北工业大学 应用物理系,天津 300401)
1 引 言
在当前的液晶器件中,响应速度慢是普遍存在的问题,蓝相液晶及其衍生相态因为具备亚微米级螺距的双扭曲结构从而具有亚毫秒的响应速度[1-3],是获得快速响应的一种重要方法。蓝相液晶在无外电场时呈现宏观各向同性[4-7],由于分子自组装特点,蓝相液晶器件具有不需要取向层,无需摩擦制备流程和无需补偿膜等特点,在光电子应用[8-14]方面成为了新的研究热点。在蓝相液晶结构中,双扭曲螺旋柱不能完全填充整个空间,蓝相液晶中存在缺陷线,在缺陷位置,液晶的排列可以被认为是各向同性相,这种晶格结构不够稳定,所以蓝相液晶存在的温度范围很窄,在拓宽蓝相液晶的温度范围方面,已经存在引入双液晶基元法[15]、弯曲型分子诱导法[16]、以及聚合物稳定[17]的方法等。在各种扩展温宽的方法中,聚合物稳定法成为最有效的方法,聚合物网络占据蓝相液晶中的缺陷位置,聚合物网络的稳定存在可以稳定蓝相液晶结构保持在一个很宽的温度范围,也能够保证蓝相液晶在电场作用下回复到初始状态,获得稳定电光特性。
液晶的响应时间反映了液晶亮暗转换速度的能力,是描述液晶器件性能的重要参数,响应时间的大小决定了显示器的刷新频率及显示器的亮度。Yan等人[18]研究了不同电场作用下聚合物稳定蓝相液晶的动态响应,并根据实验数据提出了无滞后的快速响应原理。Lim等人[19]研究了不同聚合物浓度下,聚合物稳定蓝相电光效应的Kerr系数和响应时间随温度的变化规律,电光响应时间和介电弛缓时间表现出不同的温度依赖性,在低温下聚合物对液晶分子的旋转具有足够的活性,且不受聚合物的强烈影响。Xu等人[20]基于聚合物稳定蓝相液晶的动态响应过程分别为克尔效应诱导的局部重定向和电致伸缩诱导的晶格畸变提出了双指数上升/衰减模型来分析其内在的物理机制。
在模拟计算聚合物稳定蓝相液晶的模型建立过程中,根据实验结果而提出的扩展Kerr公式能够很好地计算电场诱导的双折射率[21-22],从而实现聚合物稳定蓝相液晶显示器的模拟计算。但是,扩展Kerr公式描述的是聚合物稳定液晶在电场作用下的整体表现,不能将聚合物网络和液晶分开,也就缺少了针对聚合物稳定蓝相液晶的进一步分析。Gao等人[23]将聚合物稳定蓝相液晶中的液晶和非液晶材料分开讨论,建立了介电分压理论,获得了高介电常数聚合物材料能够提高聚合物稳定蓝相液晶的Kerr常数的结果,但依然是聚合物稳定蓝相液晶的整体表现,没有给出蓝相液晶的独立响应特性。Ma等人[24]提出了一维模型,将蓝相液晶排列视为具有较高、均匀倾斜角的胆甾相液晶,根据实验结果和建立的弹性平衡方程得到蓝相液晶的等效弹性常数,并尝试建立动力学方程来解释响应时间,该模型同样也是整体表现。目前还没有一种模型能够准确计算聚合物稳定蓝相液晶中液晶的具体响应特性,也没有相关研究能准确描述和模拟聚合物稳定蓝相液晶中液晶在电场作用下的响应和聚合物网络的作用。
本文中,模型建立在介电分压理论的基础上,根据聚合物稳定蓝相液晶显示器的实验结果,对聚合物稳定蓝相液晶中聚合物网络分压和电场对蓝相液晶的作用分别进行考虑,获得与实验曲线相符合的模拟计算结果,从而得到蓝相液晶在电场作用下的饱和电场强度和饱和双折射率,并进一步得到非液晶材料的介电常数和含量对聚合物稳定蓝相液晶器件电光特性的影响。最后,研究了共面电场驱动聚合物稳定蓝相液晶器件中电极的宽度和间隙对驱动电压和透过率的影响。该文对改善聚合物稳定蓝相液晶器件有重要的意义。
2 实验参数
在实验中,采用的蓝相液晶包含TEB300液晶(Slichem Co., Ltd., Shijiazhuang, China,清亮点温度63 ℃) 和高螺旋手性剂R5011(HCCH, Nanjing, China,螺旋扭曲力常数HTP=110/μm),聚合物单体包含双官能团单体1,4-双-[4-(3-丙烯酰氧基丙氧基)苯甲酰氧基]-2-甲基苯(RM257, Jiangsu Hecheng Display Technology Co., Ltd)和单官能团单体,单官能团单体为邻苯基苯氧乙基丙烯酸酯(OPPEA,Changshu Hengrong Trading Co., Ltd.)或2-丙烯酸十二烷基酯(C12A, Bide Pharmatech Co., Ltd.),加入少量的光敏诱发剂1-羟基环己基苯基酮(RG184, Jiangsu Hecheng Display Technology Co., Ltd.)促进光聚合反应,最终共同构成聚合物稳定蓝相液晶。具体配比如表1所示,使用的聚合物单体的分子式结构如图1所示。实验采用的IPS液晶盒的电极宽度为15 μm,电极间隙为15 μm,液晶盒厚度为10 μm。

表1 实验材料组分表Tab.1 Compositions of experimental materials

图1 聚合物单体的分子式结构。(a) RM257;(b) OPPEA;(c) C12A。Fig.1 Molecular formula of polymer monomer. (a) RM257; (b) OPPEA; (c) C12A.
3 模 型
对于IPS液晶盒这样的二维系统,首先不考虑聚合物稳定液晶中的介电常数差异,直接求解泊松方程∇(ε·∇V)=0,得到液晶层中各处的电势分布和电场分布。因为液晶和聚合物网络是在亚微米尺度混合的,所以此时的电场分布为聚合物稳定液晶中的整体电场表现。由于聚合物网络、手性剂和液晶的介电常数有较大的差异,所以在亚微米尺度下的电场强度有差别,即高介电常数的液晶和低介电常数的聚合物网络与手性剂所受的电场强度不同,所以需要进一步计算液晶中的电场强度。令C为聚合物和手性剂(非液晶材料)的总含量,非液晶材料的介电常数为εP,蓝相液晶的介电常数为εLC,根据不同的介质层有相同的电位移矢量,且电位移矢量为常数,并考虑平均电场强度得到以下公式:
(1)
其中:E为平均电场强度,ELC和EP分别为液晶和非液晶中的电场强度。由于液晶和非液晶材料的密度相差不大,所以为了便于计算,将重量比等价于厚度比,分别得到ELC和EP为:
(2)
(3)
蓝相液晶中电场诱导的双折射率[21]为:
Δnind=ΔnS{1-exp[-(ELC/Es)2]},
(4)
其中:Δnind为电场诱导的双折射率,ΔnS为液晶的饱和双折射率,Es为蓝相液晶的饱和电场强度。因为液晶的介电各向异性为正,因此诱导的介电常数也就为诱导晶体的慢轴方向的介电常数,又因为介电各向异性和双折射率都与液晶的序参数成正比,所以它们具有相同的变化趋势。液晶在电场作用下表现的介电常数为:
(5)
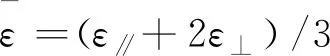
(6)
将以上步骤计算得到的介电常数εind带入泊松方程,计算得到介电常数有差异情况下的电势和电场分布,重新计算电场诱导双折射率和介电常数。经过多次迭代计算,获得准确的电势和电场分布,以及电场诱导的双折射率分布和电场方向的角度分布,在盒厚方向计算相位延迟量并计算光学特性。计算模型流程如图2所示。
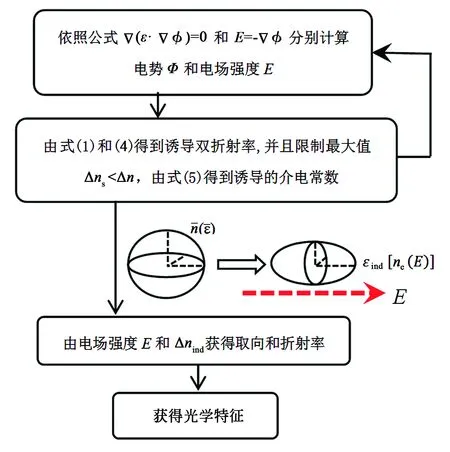
图2 蓝相液晶显示器模型流程图Fig.2 Flowchart of the blue phase liquid crystal display model
4 结 果

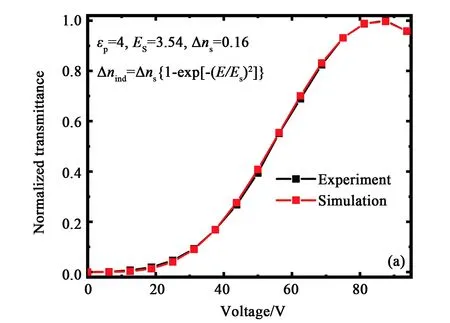
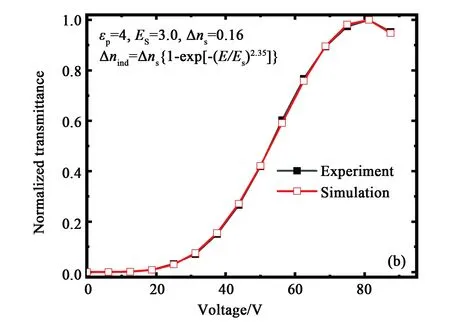
图3 模拟计算得到的V-T曲线与实验数据对比图。(a)样品A; (b)样品B。Fig.3 V-T curves obtained by simulation and experi-ment. (a) Sample A; (b) Sample B.
当对样品B进行拟合模拟计算时,不管非液晶材料的介电常数为多少,都不能得到与实验曲线符合很好的模拟计算结果,由于液晶体系与样品A相同,仅仅是单官能团单体的改变,因此令蓝相液晶的饱和双折射率和非液晶材料的介电常数与样品A中的相同,改变式(4)中的幂指数和饱和电场强度,可以得到与实验曲线符合非常好的模拟计算结果,此时的幂指数为2.35,饱和电场强度为3.0 V/μm。比较样品A和样品B中使用的单官能团单体,看到样品B中使用的单体C12A比样品A中的单体OPPEA要长且柔软,样品B的非聚合端为联苯结构,与液晶材料的刚性部分相同,也就是说,不同长度和结构的聚合物单体对液晶的束缚表现不同,最终表现为电场诱导的双折射率与电场的关系不是理想的Kerr公式关系。
应用共面电极驱动蓝相液晶器件,是工艺中最容易实现的,但在蓝相液晶显示器件的结构设计中,还没有对该结构进行优化的结果。下面,我们研究非液晶材料的含量和介电常数对驱动电压和透过率的影响,以及电极宽度和间隙对驱动电压和透过率的影响。
首先,以实验中使用的共面电极的宽度和间隙均为15 μm,液晶层厚度为10 μm为例,并使用样品A的参数来模拟计算非液晶材料质量分数为0.03~0.2和介电常数为3~30范围的驱动电压和透过率。从图4中可以看到:随着非液晶材料介电常数的增加,驱动电压下降,并且非液晶材料质量分数越大,驱动电压下降幅度越大,对于一般蓝相液晶中非液晶材料质量分数约为10%的情况,驱动电压可以从97 V(εP=3)下降到55 V(εP=30);最大透过率变化很小,可以忽略。
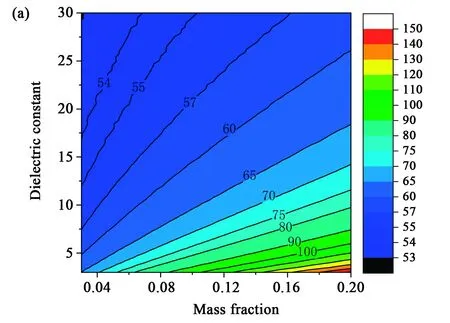

图4 非液晶材料的不同质量分数和介电常数情况的影响。(a)驱动电压;(b)透过率(电极宽度和间隙均为15 μm)。Fig.4 Influence of different mass fraction and dielectric constants of non-liquid crystal materials. (a) Operating voltage; (b) Transmittance (electrode width and gap are 15 μm).

表2 实验材料组分表Tab.2 Ingredient table of experimental materials
为研究非液晶材料不同质量分数对驱动电压的影响,我们对样品A进行了非液晶材料不同质量分数的配比,(非液晶材料含量为10%,12%,14%,此数值可固化稳定蓝相状态且效果较好),配比如表2所示。使用同样拟合方法进行拟合,实验测量电光曲线和模拟计算结果如图5(a)所示。固定饱和双折射率Δns=0.16和非液晶材料的介电常数εP=4,得到质量分数为10% 样品A1在饱和电场强度Es=3.56 V/μm,幂指数为2时的拟合效果最好;质量分数为12% 的样品A2,饱和电场强度Es=3.86 V/μm,幂指数为2.29时的拟合效果最好;质量分数为14% 的样品A3,饱和电场强度Es=4.12 V/μm,幂指数为2.26时的拟合效果最好。由图可知在非液晶材料的质量分数增加后,驱动电压增大,并且含量增加,电场诱导的双折射率与电场的关系也不满足理想的Kerr公式关系。


图5 不同含量模拟计算V-T曲线与实验数据对比图。(a)样品A; (b)样品B。Fig.5 V-T curves obtained by simulation and experiment. (a) sample A; (b) sample B.
同样对样品B进行了非液晶材料不同质量分数的配比,同样非液晶材料质量分数为10%,12%,14%,配比如表2所示。实验测量电光曲线和模拟计算结果如图5(b)所示。固定饱和双折射率Δns=0.16和非液晶材料的介电常数εP=4,得到质量分数为10% 样品B1在饱和电场强度Es=3 V/μm,幂指数为2.35的拟合效果最好;质量分数为12%的样品B2,饱和电场强度Es=3.91 V/μm,幂指数为2.25的拟合效果最好;质量分数为14% 的样品B3,饱和电场强度Es=4.63 V/μm,幂指数为2.4的拟合效果最好。由图可知在非液晶材料的质量分数增加后,驱动电压增大,并且质量分数增加,此时电场诱导的双折射率与电场的关系也不满足理想的Kerr公式关系。
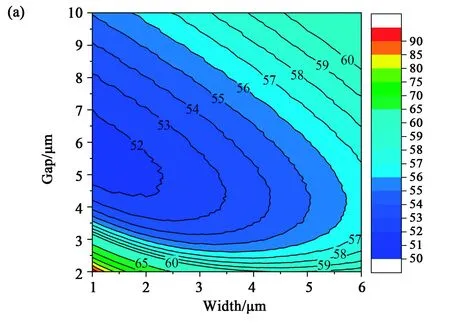

图6 非液晶材料介电常数为4时,不同电极宽度和间隙的影响。(a)驱动电压;(b)透过率。Fig.6 Influence of different electrode widths and gaps when the dielectric constant of non-liquid crystal material is 4. (a) Operating voltage; (b) Transmittance.
从图5中可以看到:样品A1具有完美的Kerr效应表现,其他样品都不具有完美的Kerr效应表现(幂指数不等于2)。考虑OPPEA和C12A的分子构型,可以认为OPPEA的联苯结构为刚性结构,其作为单官能团修饰聚合物网络时,聚合物网络表面较为光滑,对液晶的束缚较弱,从而在聚合物含量合适时,蓝相液晶表现为完美的Kerr效应,相对而言,C12A的长烷基链使聚合物网络表面更粗糙,对液晶的束缚较强,从而导致蓝相液晶表现不出完美的Kerr效应。聚合物质量分数的增加,导致饱和电场强度增大,驱动电压增大,结果符合图4的预测,但由于图4中未考虑饱和电场强度的增大,因此实验测得的驱动电压增大表现与图4 的结果有差别。
在生产线上,共面电极很容易做到5 μm以下,因此以上实验中的电极宽度和间隙不是最佳的器件参数。对于一般的聚合物单体和手性剂,其介电常数通常为4左右,如果使用高介电常数的聚合物单体和手性剂,其介电常数也能达到20左右[23, 26]。下面使用这两个介电常数研究共面电极的宽度和间隙对驱动电压和透过率的影响。为了获得饱和电压和最大透过率,模拟计算中设置电极宽度的最小值为1 μm,电极间隙的最小值为2 μm。图6为介电常数为4时的驱动电压和透过率,图7为介电常数为20时的驱动电压和透过率,此时的非液晶材料的总质量分数固定为10%(聚合物单体和手性剂的总量)。从两个图中可以得到:电极宽度为1 μm,间隙为5.5 μm时,驱动电压为最低;考虑到透过率随着电极间隙增大而增大,以及制作电极工艺技术,选择电极宽度小于3 μm,电极间隙为5~8 μm时,器件的综合性能最好,如图8计算的电压透过率曲线所示。由图8可以看到,非液晶材料的介电常数不同,仅影响驱动电压的大小,对最大透过率和电光曲线的形状影响很小。

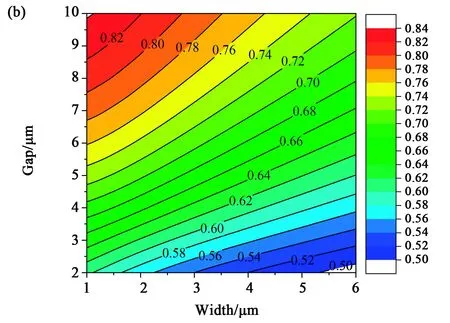
图7 非液晶材料介电常数为20时,不同电极宽度和间隙的影响。(a)驱动电压;(b)透过率。Fig.7 Influence of different electrode widths and gaps when the dielectric constant of non-liquid crystal material is 20. (a) Operating voltage ; (b) Transmittance.
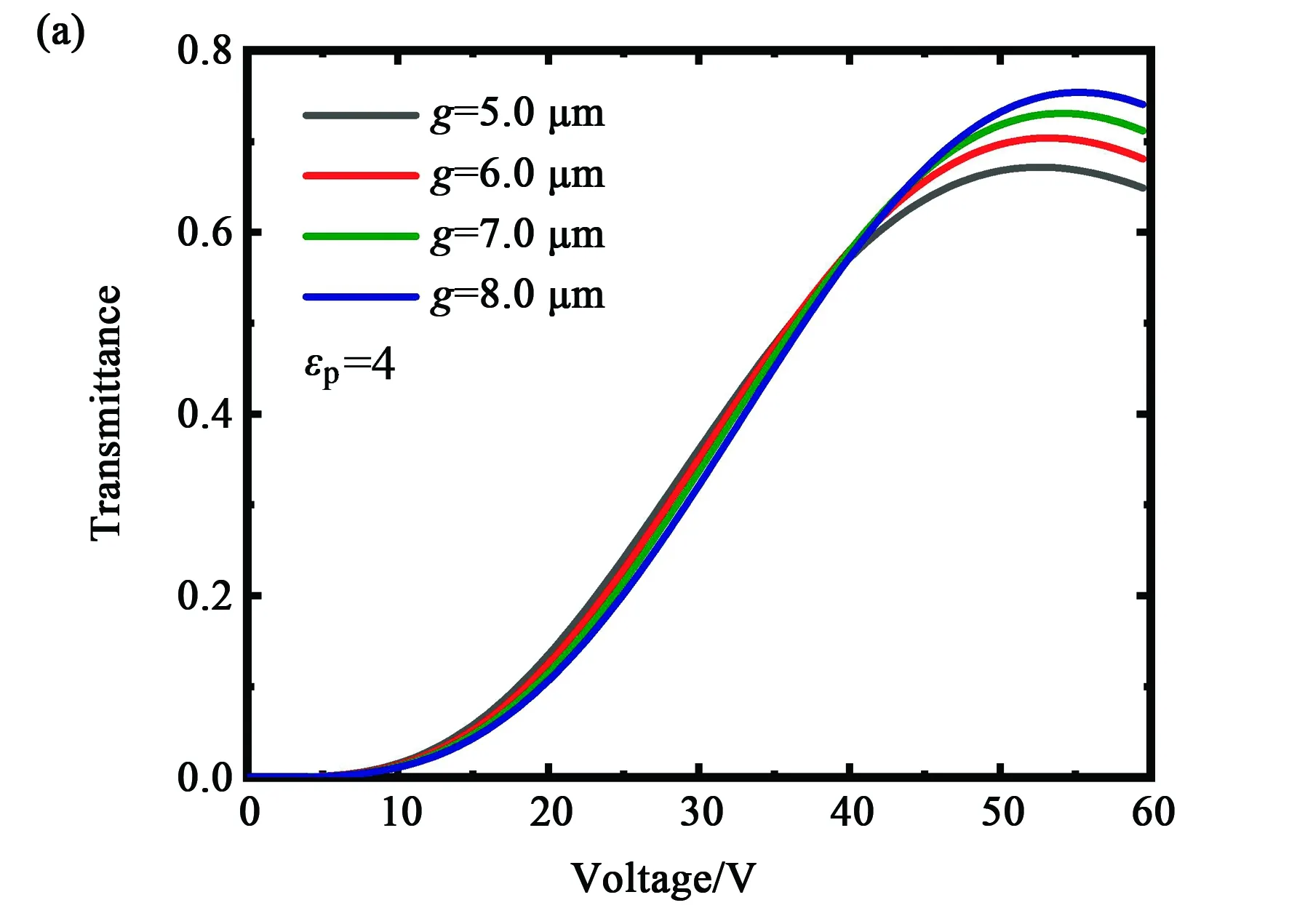
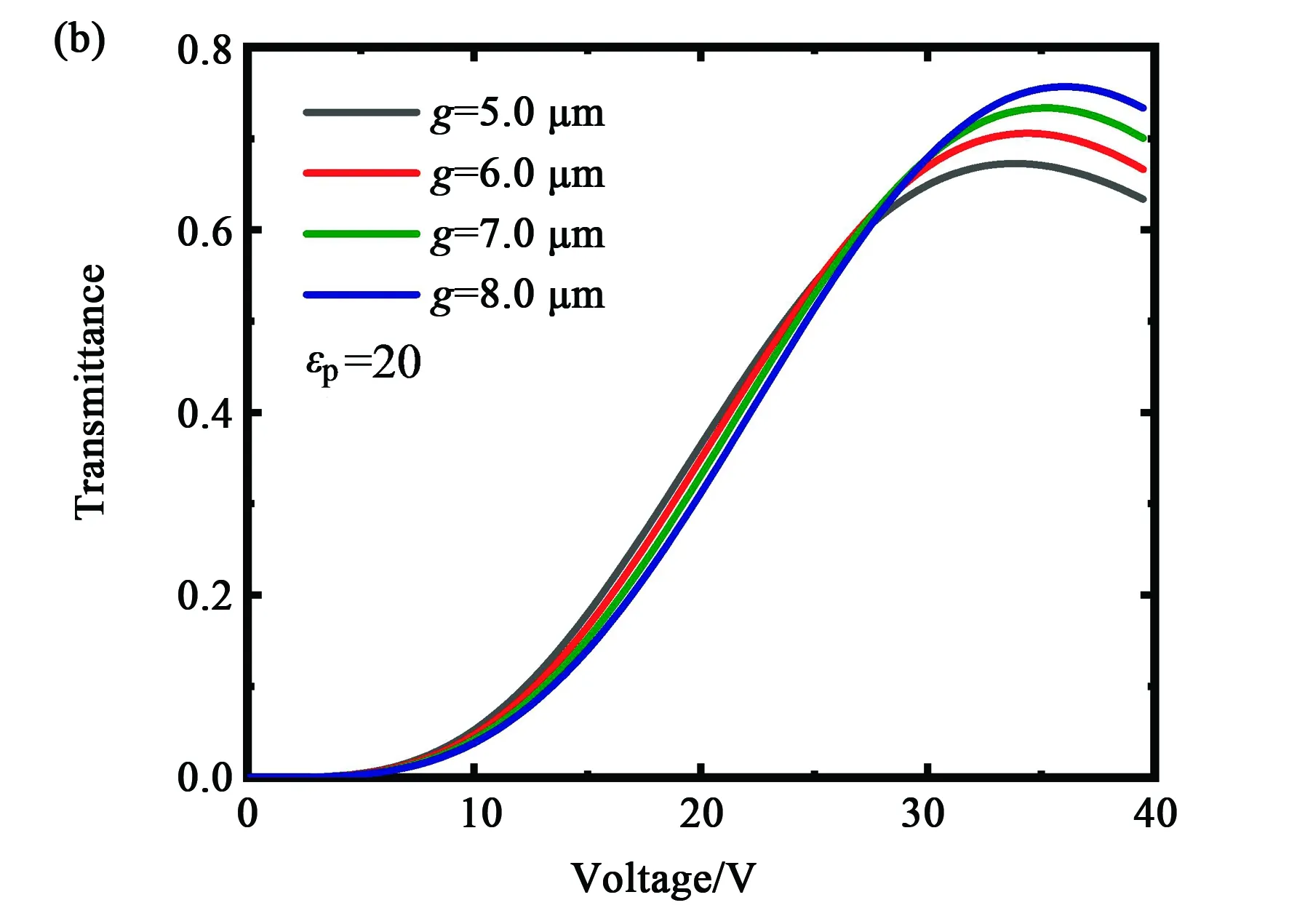
图8 电极宽度为3 μm时,不同电极间隙的电压-透过率特性。非液晶材料介电常数为4(a)和20(b)。Fig.8 Voltage dependent transmittance curves of different electrode gaps with the fixed electrode width 3 μm. The dielectric constant of non-liquid crystal materials is 4(a) and 20(b).
5 结 论
本文分别以同比例配比下的双官能团单体RM257、单官能团单体OPPEA和双官能团单体RM257、单官能团单体C12A制作的聚合物稳定蓝相液晶的实验数据为基础,研究了共面电场驱动的聚合物稳定蓝相液晶的电光特性。首先考虑了聚合物稳定蓝相液晶中非液晶材料的分压影响,得到了蓝相液晶和聚合物中的电场强度的计算模型,通过模拟计算结果与实验电光曲线拟合得到蓝相液晶的饱和电场强度和饱和双折射率,进一步研究聚合物材料含量和介电常数对蓝相液晶器件的作用,以及共面电极的宽度和间隙对驱动电压和透过率的影响。随着非液晶材料介电常数的增加,驱动电压下降,并且其质量分数越大,驱动电压下降幅度越大,对于一般蓝相液晶中非液晶材料质量分数约为10%质量分数的情况,驱动电压可以从97 V(εP=3)下降到55 V(εP=30),最大透过率变化很小,甚至可以忽略。并且非液晶材料的介电常数不同,仅影响驱动电压的大小,对最大透过率和电光曲线的形状影响很小。
本文提出的理论模型与传统的聚合物稳定蓝相液晶整体表现的理论模型相比较,具有如下的差别和进步性:(1)通过实验和模拟计算结果拟合,得到蓝相液晶的饱和双折射率接近于主体液晶的双折射率,这与整体表现的理论模型是完全不同的,我们应用胆甾相液晶中场致向列相的电场强度对蓝相液晶在电场作用下的表现进行了理论分析,确定本文的理论模型是正确的;(2)模型中区别开了聚合物和蓝相液晶中的电场强度,可以分析聚合物的介电常数对蓝相液晶器件的影响,从而可以对蓝相液晶的配方进行优化,整体表现的理论模型不能进行这个方面的分析。(3)可以得到较为准确的蓝相液晶中的电场强度,为今后的动力学响应的理论建模提供合理的电场强度分布基础。
综上所述,本文研究结果为聚合物稳定蓝相液晶器件的研究提供了可靠的计算模型和优化结果,对聚合物稳定蓝相液晶器件的发展有重要的指导意义。
