车联网环境下自动驾驶车辆动态障碍物协作避让模型

沈 悦，陈 璟，周子涵，杨 达

车联网环境下自动驾驶车辆动态障碍物协作避让模型

沈 悦，陈 璟，周子涵，杨 达

(西南交通大学，交通运输与物流学院，成都 611756)

车路协同和车联网的发展为车辆群体之间的协作控制提供了可能。本文关注的是在车联网环境下，自动驾驶车辆群体避让动态障碍物的问题，目标是实现在不损失车辆个体效益的同时，可以达到车辆群体系统最优。本文提出了一种基于深度强化学习算法(DQN)的自动驾驶车辆群体协作避让动态障碍物的模型。模型在学习过程中考虑了车辆的安全性、单个车辆和车辆群体的行驶效率，并加入了车辆的换道协作机制。仿真验证结果表明，与现有的非协作避障模型相比，该模型可以显著地提高整体交通效率，在非常拥堵、比较拥堵和自由流三种给定的不同交通流状态下，车辆行驶效率(车辆平均速度)分别提高5.26%、21.44%、10.38%，整体车流量分别提高8.22%、34.47%、0%。

自动驾驶；决策；强化学习；车辆群体；避障；车联网

0 引 言

近年来，自动驾驶技术进入了高速发展的时代，被认为是缓解交通拥堵、减少交通事故的重要技术。然而车辆在实际行驶过程中，不合理的避障行为会引发大量的交通事故，因此，自动驾驶车辆的避障决策问题成为自动驾驶领域研究的重点和热点[1-3]。

随着车路协同和车联网的高速发展，使得车辆与车辆、车辆与道路之间可以进行实时通信，这为车辆群体之间的协作控制提供了可能。当道路上存在慢车(散水车、工程车、注意力分散的驾驶员)动态障碍物时，引发交通延误，影响交通效率。因此，在图1所示典型避让动态障碍物的场景示例时，在车辆网环境下，本文搭建了一个基于深度强化学习且在目标中考虑到交通延误问题的自动驾驶车辆群体避让动态障碍物的模型。在奖励函数中引入群体效率，并通过强化学习对模型进行训练，旨在解决自动驾驶车辆群体避让动态障碍物对于车流的影响，即在不损失个体车辆效益的情况下，实现车辆群体系统最优，提高自动驾驶车辆群体的通行效率。

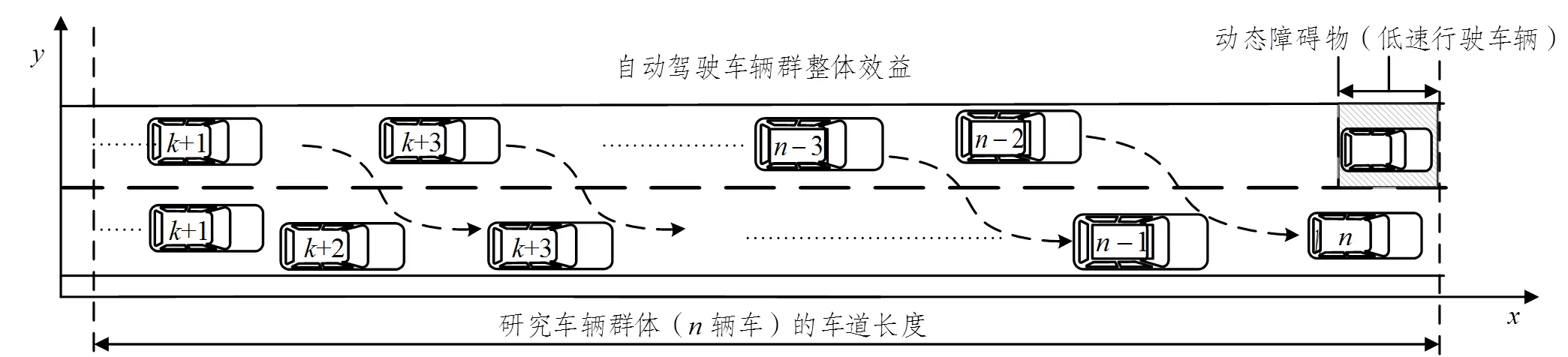
图1 自动驾驶车辆群协作避障模型问题

目前自动驾驶车辆避障的方法包含人工势场法[4-6]、快速搜索随机树法[7-10]、网格法[11, 12]、安全距离模型[13-15]、强化学习[16, 17]等。现有的一些研究也提出了自动驾驶车辆群体协作的概念[18, 19]，但没有对动态障碍物前群体协作避障问题进行探讨。同时，Piacentini等人[20]提出了调节车辆最大速度来调整交通流的车辆控制方法。Čičić和Johansson[21]提出了控制交通瓶颈中的一辆自动驾驶车辆，以最小化被控车辆延误和避免交通堵塞为目标的交通拥堵消散控制问题。Piacentini[22]等人通过研究降低移动瓶颈所在位置整体交通流的自由流速度来缓解移动瓶颈周围的影响。Čičić和Johansson[23]讨论了利用可直接控制的一部分车辆来消除停行波的问题，积累一定的受控车辆，调节交通流大小。Liard[24]等人研究自动驾驶车辆通过移动流量约束作用于交通流，改善移动瓶颈。Liard等人[25]研究自动驾驶车辆通过移动流量约束作用于交通流，改善移动瓶颈。从以上的回顾可以看出，以上的研究均为通过对自动驾驶车辆限速和调节车流量来缓解移动瓶颈问题，与自动驾驶车辆群体协作避让障碍物的研究有较大的差异。鉴于此，本文提出了基于深度强化学习[26]的车辆控制模型—— 在车联网环境下引入协作策略以交通延误最小为目标的自动驾驶车辆协作避让动态障碍物模型(a Cooperative Obstacle-Avoidance Model, COV模型)。本文使用DQN算法(Deep Q Learning)建立协作避障模型，并在换道过程中还加入车辆间的协作换道。目标是为了实现在动态障碍物前方车辆群体在安全避障的同时，保证车辆群体的效益最优，不因为避障行为而引发不必要的交通冲突和拥堵。最后，本文利用SUMO对COV模型进行了仿真验证，对比了COV模型和传统避障模型的差别，以及不同参数对于COV模型的影响。

1 决策模型

1.1 模型框架

本文所提出的自动驾驶车辆群体协作避障模型主要由三部分组成：状态信息、强化学习模块和动作模块，其结构如图2所示。状态信息为各个模块之间的输入信息，包含的内容有本车状态信息、周围车辆状态信息、障碍物状态信息、环境状态信息。强化学习模块根据当前的状态信息输出车辆的动作决策。本文基于DQN算法，假定奖励函数包括三个方面：车辆的安全性、单车行驶效率和车辆群体行驶效率，以此为衡量标准来获取车辆在环境中动作可以获取的最大累计奖励，通过接受环境对动作的奖励(反馈)获得学习信息并更新模型参数，最后达到模型的奖励收敛，实现模型在交通环境中的应用。在执行层，动作模块是对强化学习输出的动作进行执行，且加入了车辆换道的协作机制。其原理是，当强化学习模块输出的车辆动作为换道时，如若目标车道存在后车，则目标车道后车的跟驰对象变为当前决策换道的自动驾驶车辆。且当动作模块执行换道动作时，目标车道后车立即改变跟驰对象为换道车辆，对换道车辆进行避让，保证了换道动作的执行。最后，根据SUMO中自带的车辆跟驰和车辆换道模型计算出下一时刻车辆和障碍物的速度、位置和所在车道的状态信息，从而更新状态信息。

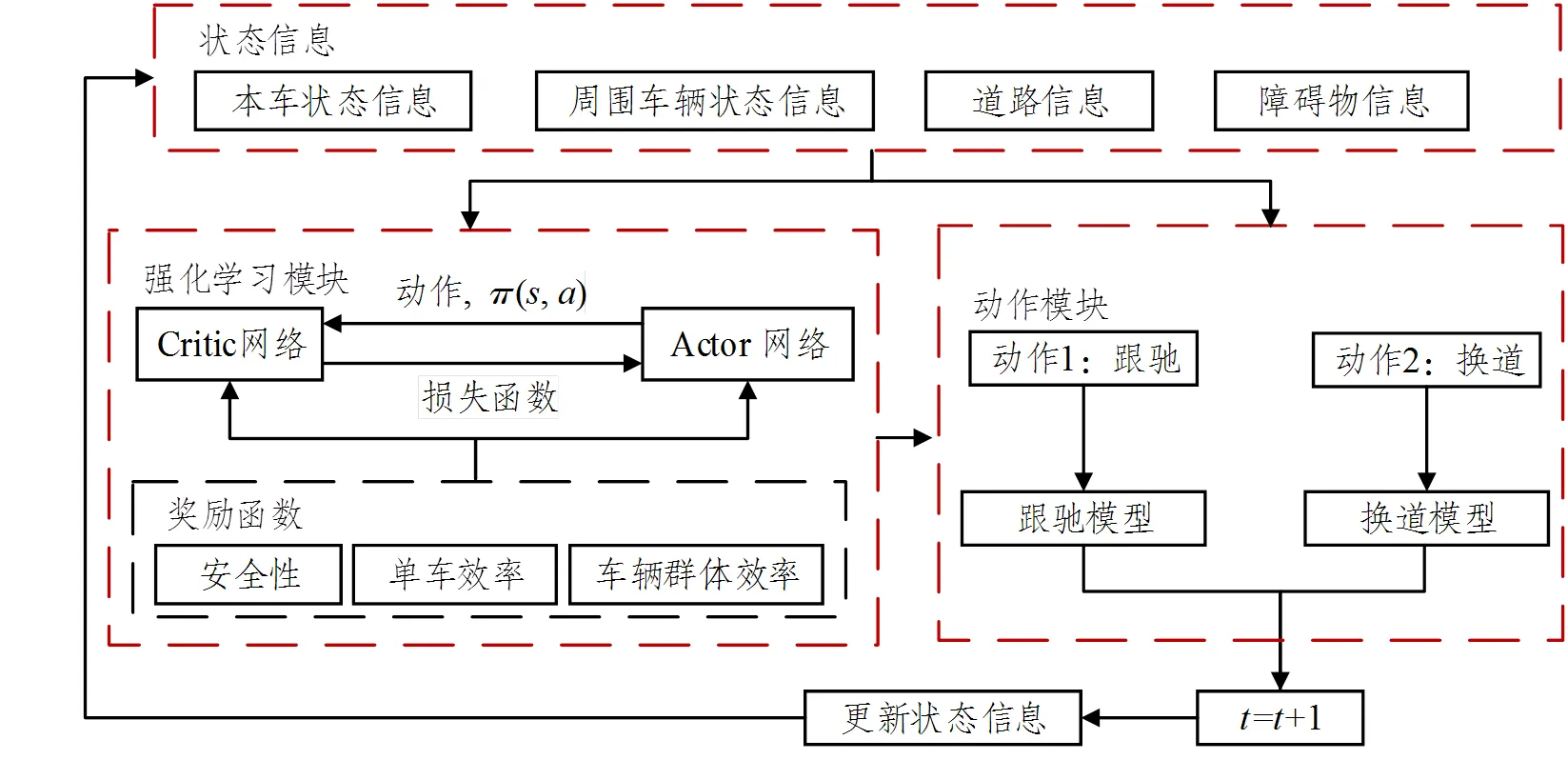
图2 模型框架

1.2 算法逻辑

在本文的研究中，在车联网环境下自动驾驶车辆在做避障决策时与过去的状态完全独立，可以被看作马尔可夫决策过程[27, 28]，表示为：

式中，s表示在时间的状态信息，包括状态信息(速度、位置、所在车道、与前车距离、与相邻车道前车距离、与相邻车道后车距离、与障碍物的距离)、动态障碍物状态信息(位置、所占用车道)、环境状态信息(车道数量、车道宽度、车道限速)；表示状态空间(s∈)；a表示在时间的动作，表示自动驾驶车辆的动作空间(a∈)，车辆的动作空间包括跟驰和换道，其分别对应SUMO自带的跟驰模型Car Following-Krauss[29, 30]、换道模型LC2013[31]。算法1总结了DQN算法的实现过程。

算法1：DQN算法 初始化容量为N的经验回放池D； 初始化动作值函数Q的随机参数； 初始化目标动作值函数的随机参数； for每个训练周期执行 初始化序列和预处理序列 for每个循环执行 以概率选择一个随机动作 否则选择 在执行器中执行动作，观察奖励值和新的场景 更新状态，并且预处理 在D中存储 在D中存储的样本中提取随机最小批量 设定 根据网络参数在上执行梯度下降步骤的方法； 每C步重新重置； end end

DQN通过计算动作值函数的值来确定损失值，其表示方法如下：

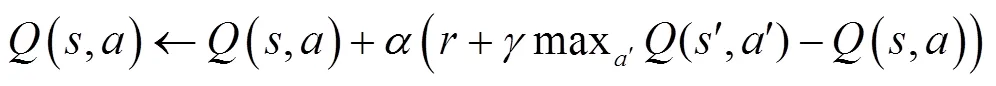
则Q网络训练的损失函数可以表示如下：

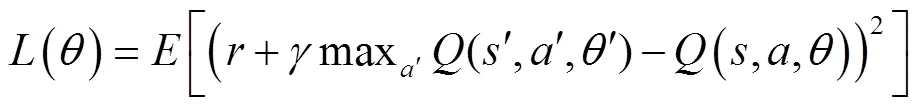
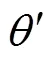
1.3 奖励函数

在本文的研究内容中，自动驾驶车辆群体在避让动态障碍物时，奖励函数追求的是车辆安全性、单车效益和车辆群体效益最大化[26]，并为三个奖励值设定了不同权重系数。

自动驾驶车辆获取的奖励值可以表示为：

式中，安全性奖励、个体效益奖励和车辆群体效益奖励的权重系数分别为1、2和3，且1+2+3=1。

1.3.1 安全性效益

车辆的安全性效益分别从跟驰和换道两种动作行为与周边车辆的安全距离、道路限速考虑，并加入了影响车辆行驶的换道奖励。

(1)跟驰行为安全性

① 安全距离

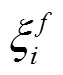
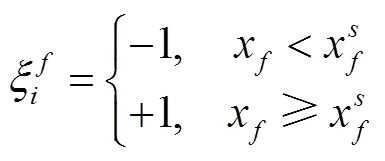
式中，x为自动驾驶车辆SV在当前车道上与前车PVt的距离；x为车辆SV与PVc的安全距离。

② 道路限速

(2)换道情况的安全性

① 与目标车道前车PVt的安全距离

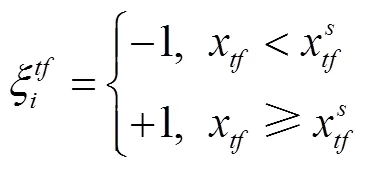
式中，x为自动驾驶车辆SV与目标车道前车PVt的距离；为车辆SV与PVt的安全距离。

② 与目标车道后车LVt的安全距离

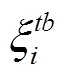
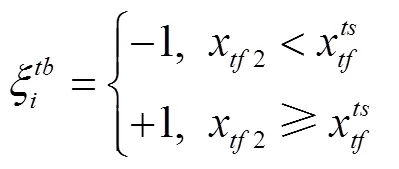
式中，x2为自动驾驶车辆SV与目标车道上后车LVt的距离；为车辆SV与LVt的安全距离。

③ 道路限速

(3)避障奖励

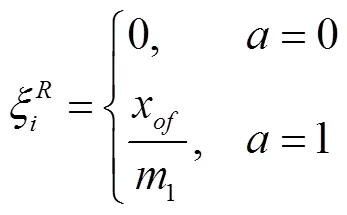
(4)避障惩罚

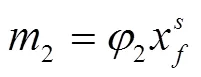
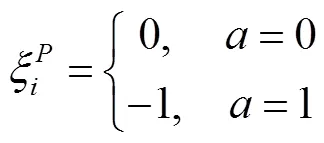
因此，关于自动驾驶车辆在安全性相关的奖励整体可表示为：

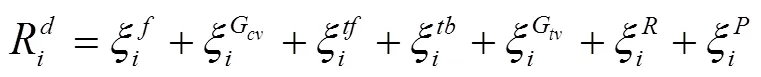
1.3.2 速度效益分析

车辆的速度效益主要从两方面考虑，个体速度效益和群体速度效益。

(1)个体速度效益

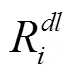
式中，max为时刻车辆群体的最大速度；min为时刻车辆群体的最小速度。

(2)群体速度效益

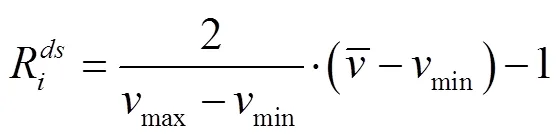
2 仿真分析

2.1 训练结果

本文利用SUMO进行仿真验证，实际仿真场景如图3所示，障碍物为浅（绿）色车辆(低速行驶的障碍物车辆)，深（红）色车辆为群体协作避障车辆，根据参考文献[33-35]，可以通过现有的互联车辆技术实现1 000 m以内的可靠通信。本文设定的车辆群体范围为动态障碍物前方700 m范围内的所有车辆，车辆超过移动障碍物则不在我们考虑的车辆群体范围内。当车辆行驶到道路尽头时，超出系统的限制范围，则删除车辆，不在系统内显示和控制车辆，并停止对该车辆的训练。具体的仿真场景中设定的环境参数如表1所示，仿真场景示意如图3所示。

表1 自动驾驶车辆环境参数

图3 仿真场景示意图

自动驾驶车辆群体协作避让动态障碍物COV模型基于深度强化学习，通过训练达到稳定的效果。本文模型进行了2 500回合的训练，利用1 000步来评估性能，DQN的学习率是0.001，衰减因子为0.9，探索率为0.9，最小探索率为0.02，探索率衰减值为0.005，其中经验内存重播样本为2 000，模型更新频率为100。图4为每回合总奖励值，表明1 500回合后获得稳定的群体控制策略。

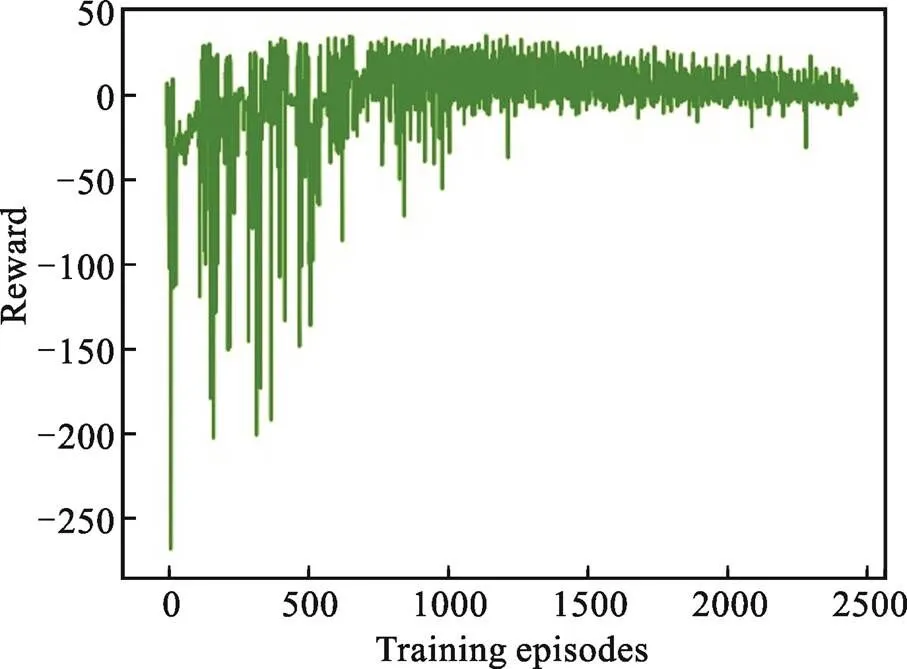
图4 强化学习训练结果

2.2 协作避让动态障碍物模型与传统障碍物模型对比

本文在初始车辆的状态信息(速度、位置和所在车道)相同的情况下，对比协作避障模型和非协作避障模型[36, 37]两种不同决策方式的输出结果。本文引用的传统模型的动作空间为跟驰和换道，且其避障决策的依据仅为单车的安全性和速度。传统避障算法的换道决策[38]如下所示：

式中，d、d，other、d，back分别表示第辆车与本车道紧邻前车的间距、相邻车道紧邻前车的间距与相邻车道紧邻后车的间距；safe表示模型中设定安全换道间距；safe为道路限速，且safe=safe。如果自动驾驶车辆同时满足公式(13)、(14)和(15)时，车辆产生换道动机，如果不同时满足，则保持跟驰的状态。

在COV模型中，训练结果设定的奖励函数的权重系数为1= 0.3，2= 0.2，3= 0.5。为了说明车辆群协作避障模型的效率，图5为COV模型与传统避障模型的车辆平均速度、车流量变化的对比情况。在本次的仿真验证中，为了展示模型在不同交通情况下与传统模型之间的对比，选取的车头时距值分别为0.5 s、1 s和3 s，三种情况分别代表交通流拥堵、比较拥堵和自由流是那种情况进行仿真验证，如图5所示。

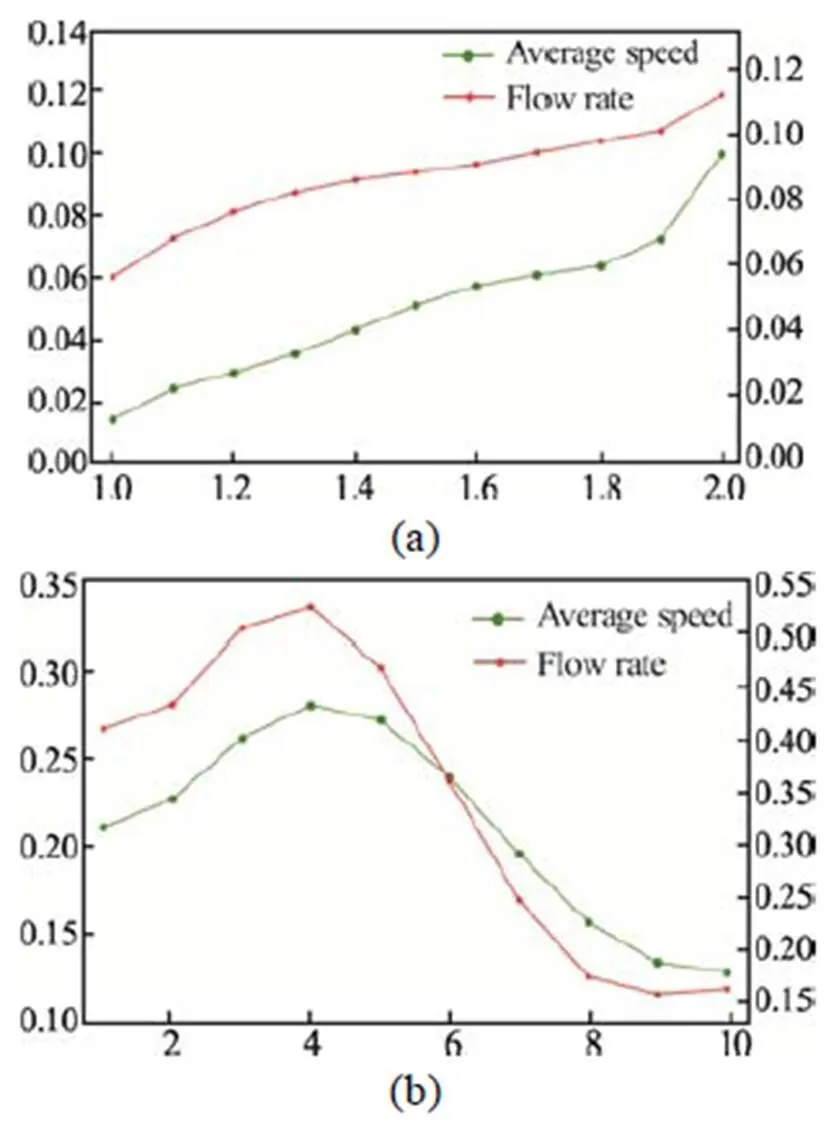
车头时距为1 s和3 s时，动态障碍物的车速从1 m/s到10 m/s等间隔选取，车头时距为0.5 s时，动态障碍物的车速从1 m/s到2 m/s等间隔选取。在三种车头时距，障碍物速度不同的情况下，本文搭建的模型与传统模型在速度和车流量上的平均提升率分别为5.26%、21.44%、10.38%和8.22%、34.47%、0%。从图中可以明显看出，在比较拥堵的时候模型的应用提升效果最好，当障碍物速度过低时，前方车辆群体的反应距离和车辆群体之间的协作时间都会减少。随着障碍物速度的增加，改进效果变好，当障碍物车辆速度为4 m/s时达到最大值，当障碍物车速再增加时，其速度更接近于正常行驶车辆，COV模型相比于传统模型的改进效果明显减弱；当在拥堵的情况下，提升效果随着障碍物速度的提高而提高；在自由流时，速度的提升效果随着障碍物速度的降低而降低，当障碍物速度达到一定值后，接近于0，这是因为处于自由流的状态，车头时距相同时，车流量两种方法相同。

本文对不同动态障碍物速度进行了仿真，形成COV模型与传统避障模型在车头时距为1 s时轨迹图，图6中(a)(b)(c)为COV模型，(d)(e)(f)为传统避障模型。障碍物速度分别为1 m/s、4 m/s和7 m/s。轨迹图中蓝色的颜色深浅代表车辆行驶的速度，红色的点划线为障碍物的轨迹线。从图中可以看出，动态障碍物车辆速度为1 m/s时，传统避障方式的障碍物车辆会影响前方车辆进入该路段，导致交通流明显减少，协作避障的方式可以更好地使车辆通过换道的方式避开障碍物。当障碍物速度为4 m/s时，传统避障模型车辆间的间距更大，障碍物前的变道行为影响车辆群体的车速和行车间距，导致车流量和车速明显减小。当动态障碍物速度为7 m/s时，速度较高，对于前方车辆群体的影响降低，COV模型仍可以通过协作的方式，减少车辆之间无效的空隙，提高交通效率。

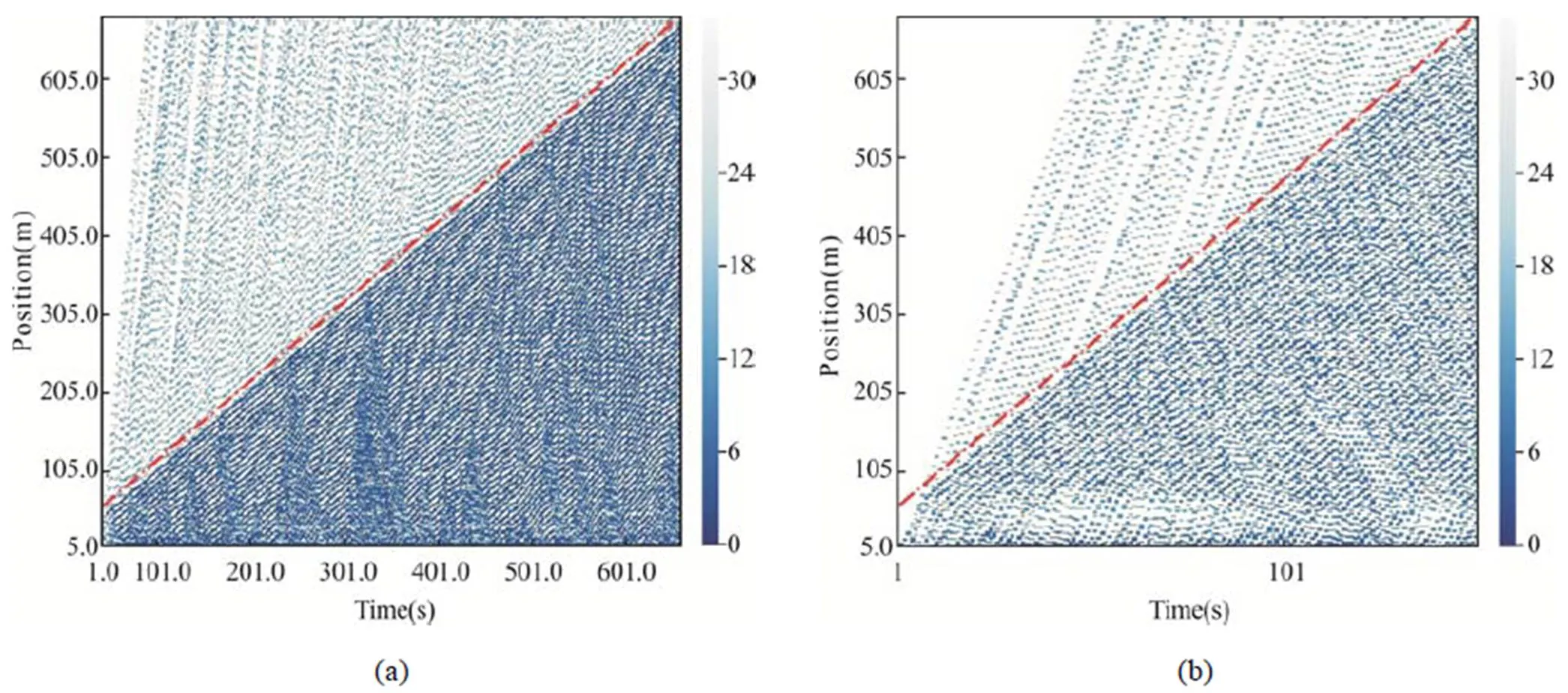
2.3 车头时距对于COV模型的影响

为了验证本文搭建的自动驾驶车辆群体协作避让动态障碍物在不同交通情况下的应用，本文选取车头时距分别为0.5 s、1 s和3 s三种情况，验证模型在拥堵、比较拥堵、自由流中的应用。如图7、8、9所示，其中图(a)为车辆平均速度和车流量随着障碍物速度变化的情况，可以看出，当车头时距相同时，车辆群体的平均速度和车流量随着障碍物速度的增加而增加，且随着车头时距的增加，平均速度和车流量增加的斜率逐渐减小。车头时距为1 s和3 s时，当障碍物速度较大时，其平均速度和车流量的变化十分缓慢，可以得出，当障碍物的速度接近于正常车辆时，对于车流的影响很小。同时，从三个图(b)中可以看出，随着车头时距的减小，车流量逐渐增加，协作配合避开动态障碍物的车辆也增多。因此，本论文提出的模型适用于不同的交通流密度，在较小交通流密度的情况下，行车间隙更小，轨迹应用效果更为明显。

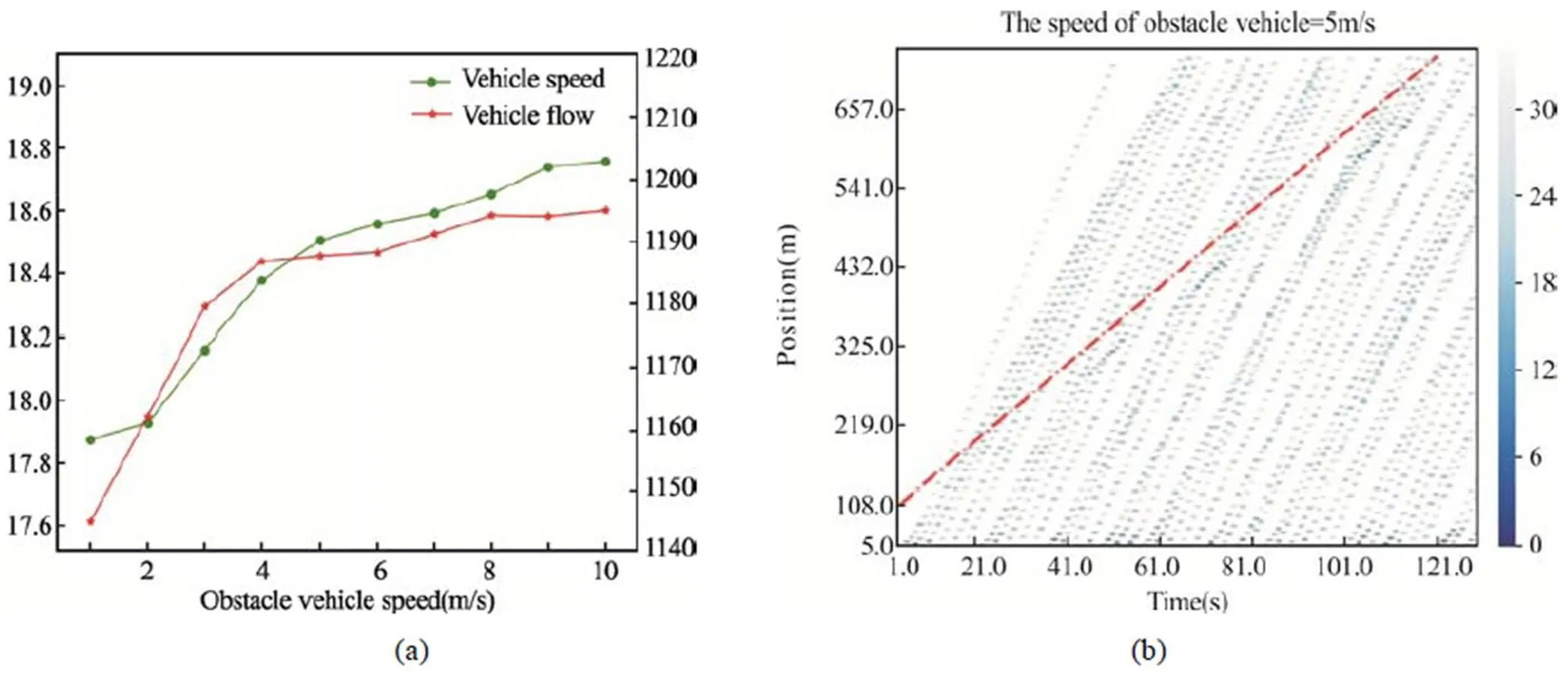
图7 车头时距为3 s时

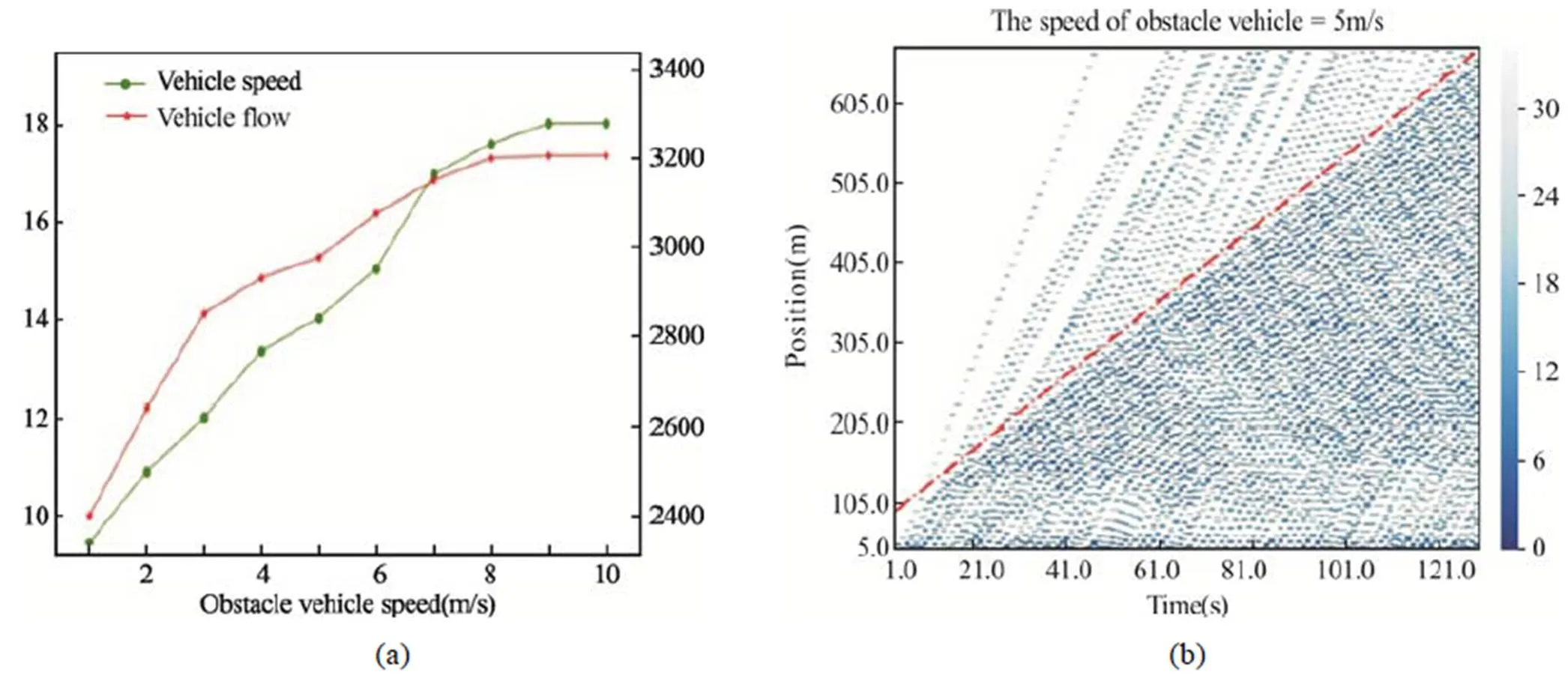
图8 车头时距为1s时

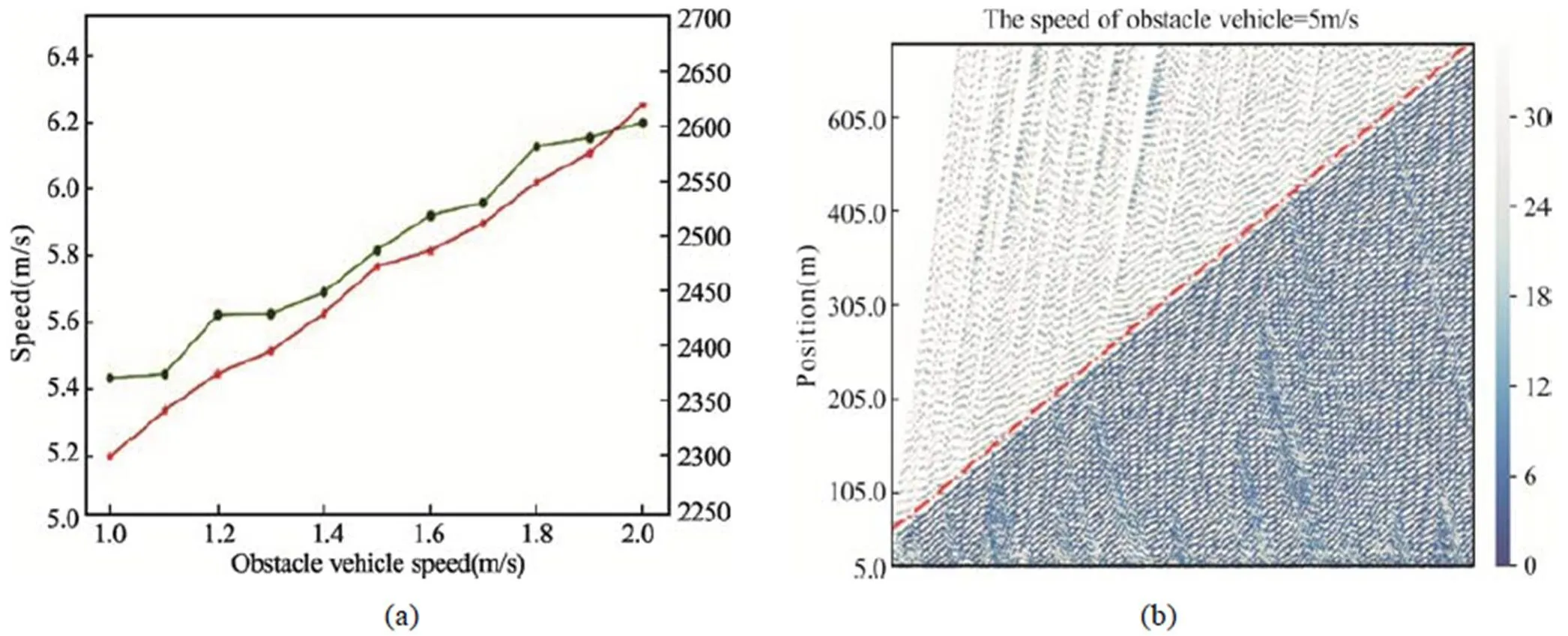
图9 车头时距为0.5 s时

3 结论与展望

本文搭建的车联网环境下自动驾驶车辆群体协作避让动态障碍物模型基于深度强化学习，在训练过程中，考虑了车辆安全性、个体车辆速度效益和车辆群体速度效益，动作空间为跟驰、换道两种行为决策，运动模块执行车辆的行为决策，并提出车辆之间协作换道的执行模型。通过仿真验证，可以得出结论：

(1)在交通环境中存在动态障碍物时，本文搭建的协作避让动态障碍物模型比传统避障模型在车辆行驶效率方面有明显的提升，当车头时距固定时，随着障碍物速度的提高，对于传统避障模型的提高效果呈现先增加再减少的趋势。

(2)本文搭建的车辆群体协作避让动态障碍物模型适用于不同车流密度，当车流量越低时，障碍物的速度变化对于车辆群体平均速度和车流量的影响程度越大，当障碍物车辆速度达到较高的值时，障碍物对于后方车辆群体的影响逐渐减小。

未来的研究工作包括两个方面：一是可以针对不同动态障碍物的情况，扩展车辆群的避让动态障碍物问题；二是除了本文使用的DQN算法，也可以尝试其他方法来解决本文关注的问题。

[1] 胡晓伟, 石腾跃, 于璐, 等. 基于扩展技术接受度模型的共享自动驾驶汽车用户使用意愿研究[J]. 交通运输工程与信息学报, 2021, 19(3): 1-12.

[2] 齐航, 夏嘉祺, 王光超, 等. 考虑出行者习惯与利他性偏好的自动驾驶网约车使用意向模型[J]. 交通运输工程与信息学报,2021, 19(2): 1-10.

[3] 徐永. 基于满意度的多目标约束模糊控制规则库的建立及应用[J]. 交通运输工程与信息学报, 2013, 11(01): 74-78.

[4] ELMI Z, EFE M Ö. Path planning using model predictive controller based on potential field for autonomous vehicles[C] // IEEE. Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society. New York: IEEE, 2018.

[5] KATHIB O. Real-time obstacle avoidance for manipulatorsand mobile robots[C]//Proceedings 1985 IEEE International Conference on Robotics and Automation, St. Louis: IEEE, 1985: 500-505,doi: 10.1109/ROBOT.1985.1087247.

[6] 修彩靖, 郭继瞬, 梁伟强. 自动驾驶避障策略研究; 2020中国汽车工程学会年会暨展览会, 中国上海, 2020[C].

[7] LAVALLE S M. Rapidly-exploring random trees: a new tool for path planning[J]. Computer. Science Dept Oct. 1998.

[8] MA L, XUE J, KAWABATA K, et al. Efficient sampling-based motion planning for on-road autonomous driving[J].IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 1961-76.

[9] 王道威, 朱明富, 刘慧. 动态步长的RRT路径规划算法[J]. 计算机技术与发展, 2016, 26(3): 105-107, 112.

[10] 宋晓琳, 周南, 黄正瑜, 等. 改进RRT在汽车避障局部路径规划中的应用[J]. 湖南大学学报(自然科学版), 2017, 44(4): 30-37.

[11] HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE transactions on Systems Science and Cybernetics, 1972, 4(2): 28-29.

[12] 马静, 王佳斌, 张雪. A*算法在无人车路径规划中的应用[J]. 计算机技术与发展, 2016, 26(11): 153-156.

[13] KOMETANI E, SASAKI T. A safety index for traffic with linear spacing[J]. Operations Research, 1959, 7(6): 704-720.

[14] LIAN Y, YUN Z, HU L, et al. Longitudinal collision avoidance control of electric vehicles based on a new safety distance model and constrained-regenerative-braking-strength-continuity braking force distribution strategy[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4079-4094.

[15] 曾德全, 余卓平, 张培志, 等. 三次B样条曲线的无人车避障轨迹规划[J]. 同济大学学报(自然科学版), 2019, 47(S1): 159-163.

[16] BAKKER L. Multi-agent deep reinforcement learning for automated Highway driving[D]. Delft: Delft university of technology, 2019.

[17] 单麒源, 张智豪, 张耀心, 等. 基于SAC算法的矿山应急救援智能车快速避障控制[J]. 黑龙江科技大学学报, 2021, 31(1): 14-20.

[18] 姬浩, 徐寅峰, 苏兵. 基于城市清洁车作业行为的移动瓶颈建模与仿真[J]. 系统工程学报, 2016, 31(5): 676-688.

[19] WU K, GULER S I. Estimating the impacts of transit signal priority on intersection operations: a moving bottleneck approach[J]. Transportation Research Part C: Emerging Technologies, 2019, 105(3): 46-58.

[20] 徐建闽, 杨招波, 马莹莹. 面向移动瓶颈的高速公路流量控制模型研究[J]. 广西师范大学学报（自然科学版）, 2020, 38(3): 1-10.

[21] PIACENTINI G, GOATIN P, FERRARA A. Traffic control via moving bottleneck of coordinated vehicles[J]. IFAC-PapersOnLine, 2018, 51(9): 13-18.

[22] ČIČIĆ M, JOHANSSON K H. Traffic regulation via individually controlled automated vehicles: a cell transmission model approach[C]// IEEE. Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems(ITSC), New York: IEEE, 2018.

[23] PIACENTINI G, FERRARA A, PAPAMICHAIL I, et al. Highway traffic control with moving bottlenecks of connected and automated vehicles for travel time reduction[C]// IEEE. Proceedings of the 2019 IEEE, 58th Conference on Decision and Control(CDC), New York: IEEE, 2019.

[24] ČIČIĆ M, JOHANSSON K H. Stop-and-go wave dissipation using accumulated controlled moving bottlenecks in multi-class ctm framework[C]// IEEE. Proceedings of the 2019 IEEE 58th Conference on Decision and Control(CDC), New York: IEEE, 2019.

[25] LIARD T, STERN R, LAURA M, et al. Optimal driving strategies for traffic control with autonomous vehicles[C]//The 21rst IFAC World Congress, 2020.

[26] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533.

[27] SUTTON R S, BARTO A G. Introduction to reinforcement learning[M]. Cambridge: MIT Press, 1998.

[28] KOBER J, BAGNELL J A, PETERS J. Reinforcement learning in robotics: a survey[J]. The International Journal of Robotics Research, 2013, 32(11): 1238-1274.

[29] KRAUß S. Towards a unified view of microscopic trafficflow theories[J]. IFAC Proceedings Volumes, 1997, 30(8): 901-905.

[30] KRAUß S, WAGNER P, GAWRON C. Metastable states in a microscopic model of traffic flow[J]. Physical Review E, 1997, 55(5): 5597.

[31] ERDMANN J. SUMO’s lane-changing model[C]// BEHRISCH M, WEBER M. Modeling Mobility with Open Data, Spring International Publishing Switzerland, 2015: 105-123.

[32] GIPPS P G. Behavioral car-following model for computer simulation[J]. Transport Research. 1981, 15(2): 105-111.

[33] NAIK G, CHOUDHURY B, PARK J-M. IEEE 802. 11 bd & 5G NR V2X: Evolution of radio access technologies for V2X communications[J]. IEEE Access, 2019, 7(70169-84).

[34] ZHOU H, XU W, CHEN J, et al. Evolutionary V2X technologies toward the internet of vehicles: challenges and opportunities[J]. IEEE Proceedings of the IEEE, 2020, 108(2): 308-323.

[35] MISHRA P K, KUMAR A, PANDEY S, et al. Hybrid resource allocation scheme in multi-hop device-to-device communication for 5G networks[J]. Wireless Personal Communications, 2018, 103(3): 2553-2573.

[36] 付智俊, 郭启翔, 何薇, 等. 基于前车意图识别的自动驾驶车辆实时避障换道策略研究[J]. 汽车电器, 2020, (12): 1-7, 11.

[37] 彭涛, 刘兴亮, 方锐, 等. 智能汽车高速换道避障安全车距仿真分析[J]. 汽车工程师, 2020(12): 36-41.

[38] RICKERT M, NAGEL K, SCHRECKENBERG M, et al. Two lane traffic simulations using cellular automata[J]. Physica A: Statistical Mechanics and its Applications, 1996, 231(4): 534-550.

Model for Cooperative Dynamic Obstacle Avoidance of Automated Vehicle Swarms in Connected Vehicles Environments

SHEN Yue, CHEN Jing, ZHOU Zi-han, YANG Da

(School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China)

The rapid development of connected vehicle technology and vehicle infrastructure cooperative systems has provided the possibility of cooperative control of vehicle swarms to avoid obstacles. This study examines the problem of automated vehicle swarm avoidance of dynamic obstacles in connected vehicle environments. The goal is to achieve an optimal swarm system without losing individual vehicle benefits. This study proposes a cooperative dynamic obstacle avoidance model for the automated vehicle swarm based on deep reinforcement learning. The proposed model considers the efficiencies of both individual vehicle and the vehicle swarm in the learning process, and a cooperative lane-changing execution model is proposed to ensure optimal decision making. Simulations showed that this model can significantly improve the overall traffic efficiency as compared with existing non-cooperative obstacle avoidance models. Under three given traffic flow conditions, namely, very congested, comparatively congested, and free flow, the increases in vehicle efficiency (i. e., average vehicle speed) were 5.26%, 21.44%, and 10.38% respectively, and the increases in overall traffic flow were 8.22%, 34.47% and 0% respectively.

automated vehicles; decision-making; reinforcement learning; vehicle swarm; obstacle avoidance; connected vehicles environment

U491.2

A

10.19961/j.cnki.1672-4747.2021.04.025

1672-4747(2021)04-0013-11

2021-04-20

2021-05-19

2021-05-26

2021-04-20； 04-21～4-26； 05-14～05-16； 05-17～05-19

国家自然科学基金项目（52172333）；中央高校基本科研业务费（2682021ZTPY010）

沈悦(1993—)，女，吉林人，研究方向为自动驾驶，E-mail：suvi_sy@163.com

杨达(1985—)，男，山西人，副教授，研究方向为智能交通、自动驾驶，E-mail：yangd8@swjtu.edu.cn

沈悦，陈璟，周子涵，等. 车联网环境下自动驾驶车辆动态障碍物协作避让模型[J]. 交通运输工程与信息学报，2021, 19(4): 13-23.

SHEN Yue, CHEN Jing, ZHOU Zi-han, et al, Model for Cooperative Dynamic Obstacle Avoidance of Automated Vehicle Swarms in Connected Vehicles Environments[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 13-23.

(责任编辑：刘娉婷)