基于改进混沌遗传算法的炮兵火力分配方法
2021-12-16丁立超
丁立超,黄 枫,潘 伟
(陆军炮兵防空兵学院士官学校,辽宁沈阳 110867)
炮兵火力分配是研究如何合理地下达炮兵射击任务,在最短时间内对敌方进行最大打击的过程。在这一过程中,炮兵火力是一定的,弹药补给是一定的,物质基础是一定的,如何安排火力分配问题就变成约束条件下最优化问题[1]。
由于混沌优化算法的随机性可以克服遗传算法容易陷入局部最优解的问题,其遍历性可以改善遗传算法的全局搜索能力。所以,将混沌优化算法与遗传算法相结合可以实现优势互补,提高遗传算法的局部搜索能力,避免出现局部最优解,有效避免遗传算法“早熟”问题。文献[2]系统论述了Logistic 映射性能,认为Logistic 映射对遗传算法初始群体算法较为有效。文献[3]对比了三种混沌映射,分别是Logistic 映射、Cat映射和Tent 映射,对它们的遍历性、初值敏感性和Lyapunov指数等方面进行了分析,得出Cat映射更适合于为遗传算法产生初始值。文献[4]把混沌扰动加入到遗传操作的交叉算子和变异算子中,提出了混沌交叉算子和混沌变异算子。文献[5]提出了遗传操作结束产生子代个体之后,在群体中添加混沌扰动,以期通过混沌扰动产生的个体中有更优秀的个体出现,加快寻优进化速度,减少寻优进化代数,提高遗传算法的搜索效率。
本文正是基于上述研究,把混沌变量应用到遗传算法中,构建了一种基于改进混沌遗传算法的炮兵火力分配新方法。
1 炮兵火力分配模型
1.1 确定火力分配原则
炮兵火力分配有诸多考虑因素,根据任务不同分配原则也会存在差异,但就普遍情况来看,以下指标必须保证。(1)最理想的打击效果;(2)最重要的射击目标;(3)同一时刻只能打击一个目标,即同一时刻每个火力单位只能攻击一个目标;(4)不同时刻,相同的火力单位可以攻击不同目标,即从第二轮攻击之后的多轮攻击可以更改打击目标;(5)当敌少我多时,火力单元优先打击价值高的目标;(6)以上假设无条件成立。
1.2 建立模型
(1)目标分配变量:xij
假设需打击目标数目为n,我方的火力单位数目为m,第i个炮兵火力单位对第j个需打击目标记为xij,于是可以得到

(2)目标价值变量:vj
(3)火力单位相关矩阵为
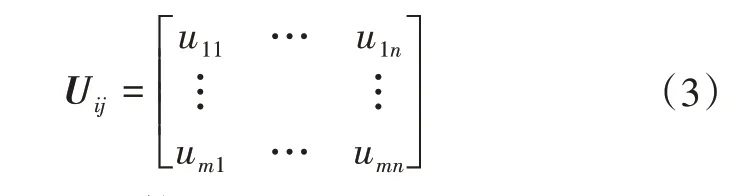
矩阵中uij表示匹配系数。
(4)目标价值矩阵:Vij
Vij表示第i个炮兵火力单位对第j个需打击目标的价值矩阵,Vij表示为
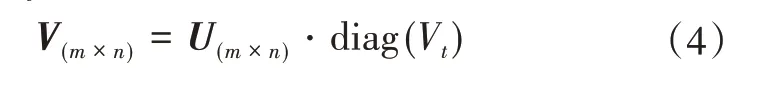
(5)射击毁伤概率:fij
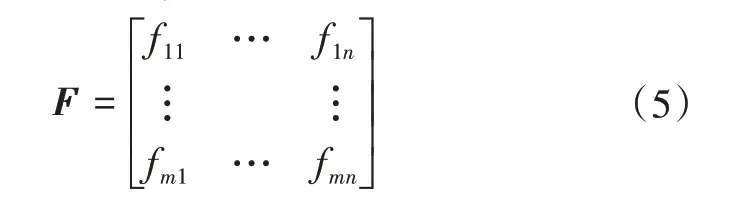
其中,0≤fij≤1,fij为第i个炮兵火力单位对第j个需打击目标的毁伤概率。当fij为0时,则表明没有打击行为。
(6)最优火力选择模型
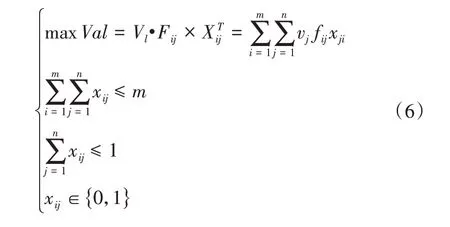
2 算法设计
2.1 编码
在编码方式上本文采用实数编码[6]。传统的二进制编码,染色体的长度与解向量是一一对应的,一个基因对应一个解向量的分量。实数编码在基因型空间和表现型空间中是一致的,可以避免编码解码带来的计算误差和时间浪费。另外,实数编码在不牺牲计算精度的前提下扩大了编码范围,对于具有约束条件的优化问题最为有效。
2.2 确定染色体的适应度函数
遗传算法来源于达尔文的生物进化论,本身对自然界和外部环境要求较低,一切最优化的评价标准和判断方法只需要计算适应度函数就可以得出。因此,适应度函数的选择恰当与否,决定了算法在优化时效率上的高低。对于经典遗传算法的适应度函数,在搜索初期,对于突出个体无法进行,导致突出个体把整个搜索过程带入局部最优而无法突破;在搜索后期,适应度函数高度一致,交叉和变异无力跳出局部范围,导致算法陷入局部最优。这主要是由于适应度函数直接被选中作为目标函数,虽然它们能够直接表现出对优化变量的适应性,但带来上述缺陷也是必然的。
对于炮兵火力分配的染色体适应度函数,应该综合考虑需打击目标和现有火力单位的情况来确定,因此适应度函数选择公式(6)中最优火力选择模型作为目标函数,然后对目标函数进行如下改进,得到新的适应度函数,即

其中,F为改进后的适应度函数值,f(X)为目标函数值,λ为特定参数。
2.3 选择+“微变异”
经典遗传算法操作使用的是轮盘赌选择,这种方式简单而且容易提取适应度函数值高的个体。但这种方式也有缺点,就是当种群中出现突出个体时,极易使搜索陷入局部最优解,而且由于适应值函数值高的个体选择性强,会更多地遗传到下一代,于是在交叉操作时,两个相同的个体容易产生无用的交叉操作,这样便降低了搜索的效率。本文在轮盘赌选择的基础之上,提出了“轮盘赌+微变异”。所谓的“微变异”是指,将复制之后的个体,进行小概率的变异,变异方式为添加混沌扰动。这样做在一定程度上减少了由于选择操作带来的“早熟”,同时也降低了相同个体之间交叉的概率。“微变异”由下式确定,即
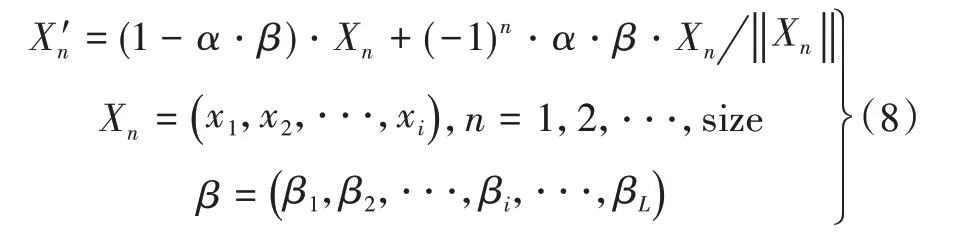
其中,X′n为新的个体,Xn为当前个体,β为混沌扰动算子,α为人工退化的影响因子,size为种群规模,L为个体长度。
2.4 自适应交叉
本文基于文献[7],提出一种改进的自适应交叉算子,该算子满足搜索算法的两个趋势。一是随着进化进程的推进,算法需要快速收敛,全局搜索的需求降低,此时的交叉算子应逐渐减小;二是对于适应度函数值高于当代平均适应度函数值的个体(假设优化问题求最大值),说明该个体因优秀更需要被保留,此时的交叉算子也应该逐渐减小。因此,改进的自适应交叉算子既与进化的代数有关,又与相应代中的适应度函数值有关;既要增加个体的多样性,又要利于快速搜索寻求到最优解。
本文改进的自适应交叉算子如下:

其中,f= max (fn,fn+1),交叉算子最大值、最小值分别为Pcmax= 0.9,Pcmin= 0.6,ρ=Pcmax-Pcmin。
交叉方式为

其中,γ为系统产生的(0,1)之间随机数。
2.5 自适应变异
本文提出的改进自适应变异算子的思路与上述改进自适应交叉算子一致,也是既考虑了进化代数的影响,又考虑了个体适应度函数值的大小。与进化代数有关是指由于到了搜索后期,主要是防止陷入局部最优解,此时的变异算子应随着代数的增加而逐渐加大,以便搜索算法能跳出局部最优。与个体适应度函数值有关是指当大于平均适应度函数值时,加大变异算子,这样就增加了个体的多样性,解决了算法后期搜索乏力的问题。基于经典实数遗传算法中的变异算子,本文提出了改进自适应变异算子,即

其中,变异算子最大值、最小值分别为Pmmax= 0.01

参数变异方式为

其中,β为混沌系统产生的(0,1)之间随机数。
2.6 混沌优化
经过遗传操作之后,对种群中适应度函数值高的个体进行保留,对低的个体进一步进行混沌优化处理。这样做可以增加种群基因多样性,使种群不易陷入局部最优解。同时,添加混沌优化可能使个体更加接近最优解,也减少了进化的代数。本文采取的混沌优化迭代公式为Tent映射,该映射公式如下:
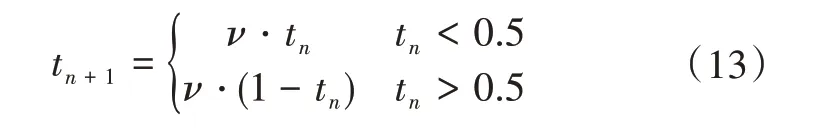
公式(13)中的ν在(1,2) 之间时,Tent 具有混沌效应,而且混沌效果随着ν增加而增强,故本文将ν设置为2 - 10-5(对Tent 迭代公式计算10000 次,记录每个点所在位置)。
混沌优化的添加方式如式(14)所示:
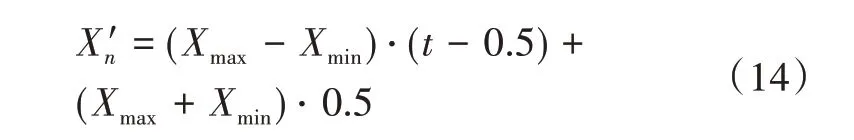
其中,Xmax,Xmin分别表示个体上限和下限。
2.7 算法实现步骤
以经典遗传算法的流程为基本流程,对种群选择操作后最好的个体进行混沌“微变异”优化,以防止早期就出现适应度函数值高的个体而导致整个种群形成局部最优,再以改进自适应交叉算子和变异算子进行遗传操作,以防止算法进化初期停滞不前,进化后期却陷入局部最优而快速收敛的缺点,为了实现混沌优化,此处引入种群早熟判定标志ε。
经计算第t代种群适应度函数的平均值为,其中为第t代种群中第i个个体的适应度函数值,N为种群规模。最优个体的适应值函数值为,所有大于的个体适应值函数值再求平均值得到。令

因此,ε小于某一阈值ε*时,种群中最大适应度个体与大于种群平均适应度个体的平均值接近,也就是说,个体的适应度值存在高度一致性,此时存在早熟风险。
算法具体实现流程如下:
Step1设定初始参数:种群规模N,混沌优化步长的调节参数φ,最大进化代数G;
Step2计算种群中每个个体的适应度函数值及对应的早熟判定标志ε;
Step3条件判断,当ε≤ε*且进化代数大于最大进化代数的一半,则对种群进行混沌优化;否则,转Step4执行。
Step4选择操作:根据式(8)完成混沌“微变异”计算;
Step5根据式(9-10)计算改进自适应交叉概率和改进自适应变异概率;
Step6进行遗传操作;
Step7判断是否满足终止条件,不满足转Step2;否则算法终止,返回当前最优解。
2.8 终止条件
当满足最大遗传代数G或者适应度函数值小于一个适当小的正数e时,遗传操作终止。
停止遗传操作后,适应度函数值最大的染色体即为所求的解,其对应的即是炮兵火力分配优化方案。
3 实例应用
假设需打击目标数为6,我方炮兵火力单位为4。需打击的6个目标分别为支撑点(j1,j2)、指挥所(j3)、轻型坦克(j4)、地面雷达站(j5),车载自行火炮(j6)。根据目标的重要程度,车载自行火炮需要3 个火力单位进行打击,其他需打击目标只需要1个火力单位。
3.1 计算目标价值矩阵
利用文献[8]提供的数据,可以得到表1和表2。

表1 目标价值系数表Tab.1 Target value coefficient table
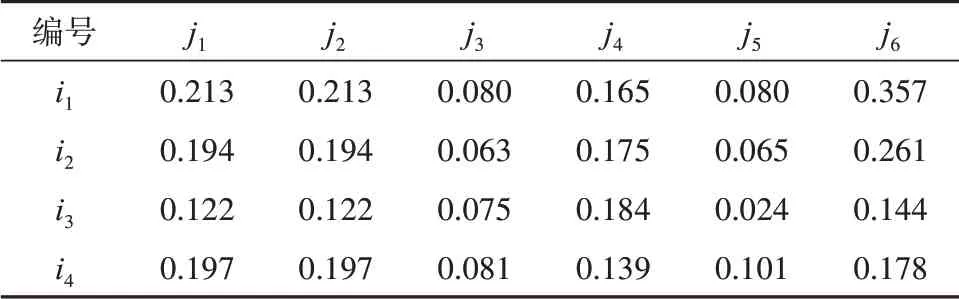
表2 火力目标相关矩阵Tab.2 Fire target correlation matrix
表1-2 中i,j分别表示我方火力单位和敌方目标。根据公式V(m×n)=U(m×n)· diag(Vt),计 算 出 目 标 价 值矩阵V(m×n)。
3.2 计算炮兵火力对目标毁伤率
根据式(5)计算可得到表3。

表3 毁伤概率矩阵Tab.3 Damage probability matrix
其中,i,j分别表示我方火力单位和敌方目标。
3.3 仿真结果分析
采用本文提出的混沌遗传算法,经过计算得到如下仿真结果,如表4所示。

表4 仿真结果Tab.4 Simulation result
从仿真结果可以看出,炮兵部队要完成此次任务,需分两轮进行攻击,第一轮攻击对象为目标j1和目标j6,第二轮攻击对象为目标j2、j3、j4、j5。该结果是综合了目标的性质、目标价值和毁伤概率等综合因素的最优结果,与实际情况相符,证明了算法的有效性。
4 结语
炮兵火力分配是一种约束条件下的最优化求解过程,是炮兵战术行动的核心部分,关系到炮兵能否完成赋予的打击任务。虽然经过多年发展,方法众多,但各种方法各有利弊,都无法保证可以得到最优方案。基于改进混沌遗传算法的炮兵火力分配模型,既利用了混沌算子的随机性和遍历性,又利用了遗传算法的全局搜索能力,克服经典遗传算法易陷入局部最优解的局限性,为解决炮兵火力分配问题提供新思路,对于炮兵作战的火力规划,快速得到较优的火力分配方案,提供了可靠的手段。
