基于正交投影的部分线性空间自回归模型变量选择

甘浩耕，赵培信

(1.重庆工商大学 数学与统计学院;2.经济社会应用统计重庆市重点实验室, 重庆400067)

0 引 言

在经济学和区域地理学中，空间模型发挥着重要作用，其中空间自回归模型在空间模型中引起了广泛的关注.关于线性空间自回归模型的估计理论，目前已有大量的文献进行了研究，比如Smirnov和Anselin(2001)利用最大似然估计方法研究了空间自回归模型.[1]Kelejian和Prucha(2010)利用矩估计(MM)和拟最大似然估计(QMLE)Lee(2004)对空间自回归模型进行了估计推断.[2]

Paelink和Klaassen(1978)指出在某些实际问题中，它们的空间关系表现的是非线性关系，因此应用线性空间自回归模型是不合适的.[3]但是由于非参数技术的发展，许多学者发现了非参数和半参数方法在建立非线性经济关系中的优势.而半参数模型又结合了非参数回归的灵活性和线性回归的简洁性，比起非参数模型提供了更多的可解释性.在关于空间问题的半参数统计推断中，Gress(2004)提出了两种半参数空间自回归模型，并与大量的参数空间自回归模型进行了比较.[4]Su和jin(2009)结合拟似然方法和局部多项式方法对部分线性空间自回归模型提出一个估计方法.[5]Du等(2018)则利用B样条近似部分线性空间自回归模型的非参数部分，并利用工具变量给出了估计方法.[6]关于部分线性空间自回归模型的更多研究参见文献罗国旺和吴密霞[7](2020)以及谢琍(2019)等.[8]

本文则研究部分线性空间自回归模型的变量选择问题.通过B样条逼近技术和正交投影方法，对部分线性空间自回归模型提出了一个基于正交投影的变量选择方法.所提出的方法利用工具变量调整技术解决了空间数据的内生性，并且结合正交投影技术，消除了非参数部分对参数部分变量选择的影响，进而保证了变量选择的有效性和相合性.

1 模型统计理论基础

1.1 正交投影

投影在线性代数和泛函分析中给出定义：从二维向量空间中的映射投影到自身的一种线性变换，是在日常生活中“平行投影”这个基本概念的具体化和系统化.投影变换本质就是一种映射，[9]其是将整个向量空间映射到它的其中一个子空间，并且投影的过程在这个子空间中是恒等变换的.在内积空间中，正交投影是指像空间U和零空间W相互正交的子空间的投影，也就是说，在任意的u∈U,w∈W下,他们的内积是(u|w)=0.而如果投影是在实向量空间中，那么它对应的投影矩阵是对称矩阵.本文的研究则基于在实向量空间中，运用矩阵的QR分解，再利用正交矩阵的性质，消除模型非参数部分对模型的影响.

1.2 B样条基函数

首先给出定义：

在这里，B样条有n+1个控制点Pi.其中k表示B样条曲线的阶数，k-1表示B样条的次数.

B样条基函数是一个非递减的参数为t的序列所决定的k阶分段的多项式.设t是n+1个非递减数的集合，其中t0≤t1≤t2≤…≤tm.ti称为节点,集合t称为节点向量,那么半开区间[ti,ti+1)则是第i个节点区间.假设某个节点出现了k次 (即ti=ti+1=…=ti+k+1), 其中?k>1,ti是一个重复度为k的多重节点，记为ti(k).如果某个节点ti只出现了一次，那么它就是一个简单节点.而如果节点是等间距的(即ti+1-ti是一个常数，0≤i≤m-1)，那么就称节点向量或节点序列为均匀的，否则它就是非均匀的.本文将应用B样条基函数处理非线性函数g(·)，将其转变成基函数的线性组合形式.

1.3 两阶段最小二乘法

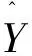
1.4 SCAD方法

SACD变量选择方法由Fan和Li提出的一种基于惩罚的变量选择方法.[9][10]在众多变量选择方法中，该变量选择方法能够同时做到选择重要变量和估计模型系数.SACD罚函数是对称并且在零点是奇异的，从而能使得惩罚估计产生稀疏解并达到变量选择的目的.SCAD惩罚函数的一阶导数具体形式如下：

其中a为大于2的参数，λ为调整参数，自变量θ满足大于0.目前，SACD惩罚方法已被推广到非参数模型及半参数模型的变量选择中，并具有较好的变量选择效果.本文将SCAD惩罚方法运用到部分线性空间自回归模型的变量选择中，进一步改进和推广了SCAD变量选择方法的应用领域.

2 基于正交投影的变量选择过程

给出经典的部分线性空间自回归模型

Yn=ρWnYn+Xnβn+g(zn)+Vn

(1)

其中Yn=(y1,…,yn)T是因变量观测值的n维向量；ρ是标量自回归参数；Wn是已知常数的n×n空间加权矩阵；Xn是n×pn线性回归的观测矩阵；βn=(βn1,…,βnpn)T是Xn的pn×1未知回归向量关联系数.zn是非参数回归变量的n维向量；g(·)是zn的一个未知函数，Vn=(v1,···,vn)T是独立同分布的n维模型误差向量，并且具有零均值和有限方差σ2.

首先将应用多项式样条来近似非线性函数g(·)，通过工具变量法来处理模型中具有内生性的空间滞后项，再构造π(z)=(B1(z),B2(z),···,BLn(z))T作为一个B样条基函数，其中Ln=kn+l+1，kn为内部节点个数，l为B样条阶数，那么给出拟合公式：

其中α=(α1，···,αLn)T. 设∏=(πT(z1),πT(z2),···πT(zn))T，那么模型(1)可以重写为：

Yn=ρWnYn+Xnβn+∏α+en+Vn

(2)

结合矩阵Π利用矩阵的QR分解可得：

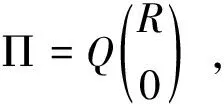
令Q=(Q1,Q2)，其中Q1是n×Ln阶矩阵，Q2是n×(n-Ln)阶矩阵.

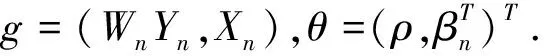
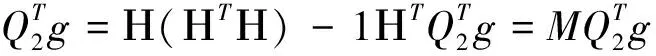
(3)

因此样条系数向量α的估计为：

(4)

通过引入工具变量，模型1则改写为：

为了将工具变量的应用有效化，将矩阵Yn回归得到ρ和α，再通过回归变量WnYn,Xn,∏构造如下的工具变量：

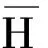
再给出SCAD罚函数的一阶连续导数：

其中a为大于2的参数，λ为调整参数，自变量满足t大于0，SCAD惩罚进行参数估计和变量选择时可以同时进行，并能为回归系数产生稀疏解和无偏估计.

在实际数据分析中，我们不知道Xn中的哪个协变量很重要，于是使用SCAD惩罚对回归系数进行估计，即定义带有惩罚项的目标函数L(θ)如下：

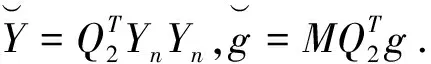
3 变量选择相合性

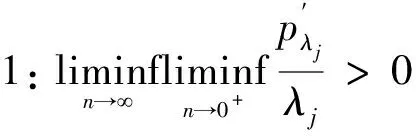
假设2：zn的分布是绝对连续的，并且其密度在[0，1]上均匀从零开始.

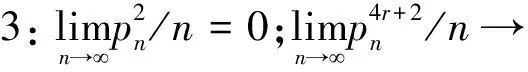
假设4：矩阵(In-ρWn)是非奇异的且|ρ|>0，(In-ρWn)与Wn的行和列之和的绝对值一直有界.

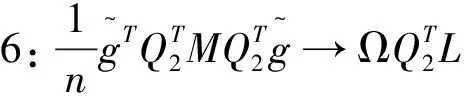
假设1使得惩罚函数在原点处是奇异的，因此惩罚估计量具有稀疏属性.假设2使得协变量具有有界条件.假设3限制了协变量的增长速率.假设4是为了更好契合空间自回归模型的设置.假设5是为了工具变量而设置的.假设6要求所生成的回归变量Xn偏离其在zn上的非参数投影，并不是渐近多重共线性的.

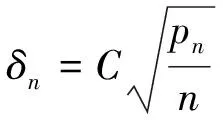
通过使用泰勒展开式，我们得到：

然后，我们得出：

根据假设1可以得出，n→∞

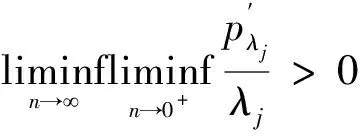
因此导数的符号完全由βj的符号确定，所以由(5)可知，定理证明完毕.