考场构建“模型” 思维探究“设计”

摘 要：通过透析2021年中考物理命题最新动态，对一道压轴题的微观思维探究过程展开分析与思考，让笔者感受到 “教的逻辑”与“学的逻辑”急需转变，未来教学将是进阶性的.教师在日常教学中常采用“真实情境”导入学习目标，设置“系列任务”和“问题嵌入”，通过一系列学生“自主探究”活动实现深度学习可能代表着未来的一种学习方式.

关键词：中考物理;思维探究;杠杆;项目

中图分类号：G633.7     文献标识码：B     文章编号：1008-4134（2021）24-0055-03

基金项目：芜湖市2019年安徽省重点课题“基于项目学习的中学物理深度教学实践研究”（项目编号：JKZ19004）.

作者简介：滕元斌（1970-），男，安徽芜湖人，本科，中学高级教师，研究方向：中学物理课堂教学、中考研究.

1 试题呈现

2021年安徽省中考物理试卷第23题是一道思维探究题（如图1所示）：在研究物理问题时，常需要突出研究对象的主要因素，忽略次要因素，将其简化为物理模型.

如图1甲所示，一质量分布均匀的杠杆，忽略厚度和宽度，长度不可忽略，用细线将它从中点悬起，杠杆能在水平位置平衡.将它绕悬点在竖直面内缓慢转过一定角度后（如图乙所示）释放，为研究其能否平衡，可将它看成等长的两部分，请在图乙中画出这两部分各自所受重力的示意图和力臂，并用杠杆平衡条件证明杠杆在该位置仍能平衡.

如图丙所示，一质量分布均匀的长方形木板，忽略厚度，长度和宽度不可忽略，用细线将它从AB边的中点悬起，杠杆能在水平位置平衡.将它绕悬点在竖直面内缓慢转过一定角度后（如图丁所示）释放，木板在该位置能否平衡？写出你的判断依据.

本试卷一改历年安徽省物理中考试题计算与推导题的总体设计，推导题作为初高中物理衔接的重大体现，一直是安徽省中考题的必考题型，而它的分值一直是4分或5分，相对比较稳定;且一般是相对比较容易过渡的公式推导或情境问题解答.而今年一改常态，作为最后一题，有推导、计算、说理与运用，分值在总分下降的前提下还提高至8分，显然，设计者已将它设置成压轴题.从甲图到丁图的思维进阶，是一种必须沉浸其中后方能较全面地完成思考探究的“项目”研究.从某种意义上说，它是升级版的考场科学探究活动.

2 思路剖析

2.1 设计意图

表面上看它只是考查学生杠杆模型与杠杆的平衡条件，但实际上它同时兼顾学生日常思维探究的考查、物理知识的综合运用、生活化问题的思考研究、重力知识、数学中全等和解三角形等知识的实际运用.在一定程度上考查学生科学思维的深度学习，通过考后统计分析，笔者认为本试题的难度偏高，区分度较好，是一道力求让学生进行实时现场探究（一个项目）与充分发挥学习用具功能（一物多用）等能力的优秀试题.

2.2 思路一

第（1）小题的回答难度不大，正确率较高，答案是：杠杆在该位置仍能平衡.杠杆两部分各自所受重力的示意图和力臂如图2所示，设杠杆的长度为L， 所受重力为G，杠杆转过的角度为θ.

解法1：基于对杠杆平衡条件的认识，分析得出杠杆两边可看成两部分，质量均匀，两侧等重（力相等），中点悬起（支点），两侧力臂相等，因此G1×L1=G2×L2，再进一步联想到平时的探究实验，将它绕悬点在竖直面内缓慢转过一定角度后（如图1乙所示）释放，此时力与力臂还是相等的，因此G1×L1=G2×L2 ，所以杠杆在该位置仍能平衡.

解法2：利用数学知识全等三角形对应边相等，如图2所示，可以直接利用数学知识，易证△AOO1≌△BOO2，因为OO1=OO2=12L，所以L1=L2，G1=G2 =G2，所以可得G1×L1=G2×L2，所以杠杆在该位置仍能平衡.

解法3：由图2可知（利用数学知识，三角函数知识）：

L1=L2 =14L·cosθ，G1=G2 =G2.可得G1×L1=G2×L2，所以杠杆在该位置仍能平衡.

评析：解法1、解法2、解法3在思路上有明显层级之分，与学生的思维方式密切相关，解法1更符合初中学生的思维模式，而从命题建模思想出发，命题人最想得到的是解法3，而本题若只有第一小题，那么上述同学的不同解法区分基本无效.好在本题设计成思维探究题，接下来学生还要面对第2小题的挑战，所以在进行进一步深入思考之后，又会有许多同学在下一步解题中重复上述思路.可见解法1考查学生语言表达与逻辑思维能力的综合运用，而解法2与解法3的出现则是数学建模思想的运用，简化问题数学化，更显简捷.从学生思维“项目化”不断进阶的探究而言，最终让学生明白杠杆平衡不一定在水平方向.

2.3 思路二

第（2）小题是在第（1）小题的思路之下，进一步拓展，并与实际宽度不可忽略相联系，答案要求学生只要“能利用杠杆平衡条件或力的平衡条件简要表述不能平衡的原因即可，对重心位置、力臂大小、力的大小等判断过程不做要求”，而笔者认为学生对知识的感性认识很有必要.继第（1）小题的解答之后，学生可以运用前面的物理量进行推理或解答，最终得出：不能平衡.

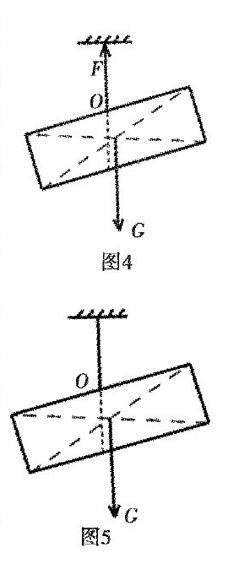
解法1：（杠杆平衡条件法）将木板看成左右相同的两部分，各自所受重力和力臂如图3所示，设木板所受重力为G，由图可知L1

解法2：（二力的平衡法）木板转过一定角度后释放，其受力情况如图4所示.

此时木板的重心已偏向右侧（如图4所示），可知木板受到的拉力F和重力G不在一条直线上，不满足二力平衡的条件，所以木板在该位置不能平衡.木板会绕O点，顺时针转動，直到最终在水平位置保持平衡.

解法3：（整体杠杆法）如图5所示，将木板看成一个整体，此时重心在几何中心，由图可知重力的方向与支点不在一条直线上.

对于一个杠杆而言，只有一个力，且它的力臂不为零，所以杠杆不能平衡.

评析：从学生视角看，解法1更符合初中学生的思维模式，而从命题人的建模思想出发，最想得到的是学生思维的进阶——发散思维，充分利用题意保持平衡，也就是静止状态.这样能够得出解法2和解法3，可见解法1考查学生思维能力的综合运用，而解法2与解法3的出现则是物理建模的进一步推广，让学生在充分运用题意之下，发散出思维的火花，相对而言，解法更直接、更简洁明了.

3 教学启示

通过对中考“压轴题”的解法分析，笔者发现试题在继承历年中考推导题的基础上，进一步拓展科学思维与核心素养，对学生科学探究、科学推理进行全新的考查，同时注重将物理模型的运用过渡到基础知识、思维能力的综合考查.而从数学、语文角度的学科整合又让我们看到学生考场思维探究的作用和意义.这种考查方式更类似于目前比较流行的项目式学习方式.

3.1 “教的逻辑”转变——情境性

透析目前中学物理日常教学的诸多实践，在落实物理模型教学与学生能力发展教学上，现实与理想依然存在一定差距，通过对2021年安徽中考压轴题23题解法与考查要求的分析可见，教师在今后的物理教学中一定要注重体现建模活动的过程性.让学生充分融入活动过程中，比如当前较热门的“项目式学习”的系列活动、系列任务、系列问题……等过程，就能让学生在教师引导下的自主、合作、研讨及交流中，更充分地体验建模过程的情境性（真实情境）.因而作为教的主导者，教师必须转变“教的逻辑”：“教”的“目的”是为了学生更好的“学”，教的最高境界是“不教”，从而能达到落实核心素养的目的.

3.2 “学的逻辑”转变——进阶性

压轴题象征中考的选拔性特征，它要求学生在考场一定时间内，充分体验知识与能力的内化、拓展过程，使学生日常学习中深层次的思维过程得以体现、得到评估，这实际上是一个学习过程从简单到复杂、从间断到连续的推理认知发展的过程，未来的物理学习更趋向于思维的进阶.学生一味机械式的记忆，实际上已无法适应这样的考查过程.学生的学习过程要转变，达到思维越开放，答案越接近命题的目的.

当前项目式大单元设计背景下的教学实践，体现当下活动设计的基本模式：学生自主设计方案、小组交流与研讨、师生互动、生生互动、学生自主评估、主题研讨、撰写学习心得体会、制作学具或“产品”、归纳系列解题方法与策略等全新学习形式，让更多学生在“学的逻辑”上得以转变，最大限度地提升学习效率、学生个人能力与群体层次，从而实现学习方式的真正转变，它让学习水平的层次像一个个“台阶”具有一定的梯度，学习的方式不断得以进阶——从简单到复杂、从间断到连续.

总之，根据当前的物理教学实际，学生的认知水平大多停留在记忆、再现这一浅层学习状态，思维得不到提升，能力得不到发展，课堂也是低效的.在项目学习中通过中考压轴题的深入思考，让我们明确，在今后的物理课堂教学中，教师的“教”和学生的“学”的观念均要紧跟时代（特别是中考）的步伐.当前大量实践经验告诉我们：教师在日常教学中常采用“真实情境”导入学习目标，设置“系列任务”和“问题嵌入”，通过一系列学生“自主探究”活动实现的项目学习可能代表着未来的一种学习方式.在这种的教学过程中，教师的教学行为和目的不是单纯地让学生进行知识的记忆性迁移，而是要引导学生通过自主学习、交流、合作探究来解决开放性问题并完成学科知识的建构.

参考文献：

[1]翟小銘，郭玉英，李敏.构建学习进阶：本质问题与教学实践策略[J].教育科学，2015，31（02）：47-51.

[2]中华人民共和国教育部.普通高中物理课程标准（2017年版）[M].北京：人民教育出版社，2018.

[3]夏雪梅.项目化学习设计：学习素养视角下的国际与本土实践[M].北京：教育科学出版社，2019.

[4]陈琪.初中物理教学中培养学生科学思维的策略[J].读写算，2021（20）：61-62.

[5]刘菊贤.科学思维视角下的初中物理教学研究[J].名师在线，2021（18）：62-63.

（收稿日期：2021-07-14）