基于多物理场耦合永磁同步电机边带电磁噪声分析
2021-12-15胡世同邱子桢成海全魏长银张黎明
胡世同,邱子桢,2,陈 勇,成海全,魏长银,张黎明
(1. 河北工业大学 天津市新能源汽车动力传动与安全技术重点实验室,天津 300130;2.哈德斯菲尔德大学 效率与效能工程中心,英国 HD1 3DH)
永磁同步电机是目前新能源汽车电驱动系统搭载的主要电机类型,由于失去了发动机的掩蔽效应,电机的高频噪声成为影响电驱动系统NVH 性能的主要噪声源,是当下研究的热点[1]。尤其对于普遍采用空间矢量脉宽调制(SVPWM)技术驱动的永磁同步电机,边带电流谐波将不可避免地在载波频率附近被引入。由边带电流谐波产生的电枢磁场与永磁体磁场相互作用将产生边带电磁力并导致高频电磁噪声,严重影响电机的声品质[2]。
为分析边带电磁力特性,Liang 等[3-6]建立了基于SVPWM 的边带电流分析模型,指出电机运行过程中会在载波频率及其整数倍频附近产生电流谐波分量,并推导了整数槽与分数槽电机的声振分析方法。Deng等[7]对搭载SVPWM技术的内外转子永磁同步电机的边带电磁力进行了对比分析,揭示了极槽组合对边带电磁力时空特征的影响,为永磁同步电机的噪声源识别提供了理论依据。为研究永磁同步电机振动噪声,文献[8-10]建立了电磁与辐射噪声的多物理场分析模型,并对比了齿面集中力与分布力的振动分析结果。于慎波等[11]基于永磁同步电机噪声试验的频谱特征,分析了电机转频、电磁力频率及载波频率对噪声峰值的影响。文献[12]通过建立电磁力与声压级之间的噪声传递函数对永磁同步电机辐射噪声进行评价分析。
目前对于边带电磁噪声的研究主要集中在降噪方法及调制策略上,如随机调制技术[13]与可变开关频率技术[14]等,往往是采用降低能量幅值或提高载波频率的方法来控制电磁噪声,针对特征频率段的主动控制优化研究较少。若要在实际工程应用中实现电机NVH性能的主动优化,仍需要进一步对边带电磁噪声特征进行分析。
因此,为揭示由载波频率引起的边带电磁力与辐射噪声间的关系,并对边带电磁噪声进行准确预测,本文对搭载SVPWM 技术的永磁同步电机的边带电磁噪声进行了深入研究。通过解析法推导归纳了边带电磁力的时空特征,并基于多物理场耦合建立了电机声振分析模型,对一台12槽10极永磁同步电机的边带电磁力与辐射噪声进行了有限元分析,最后通过样机试验验证了解析与仿真的准确性。研究有助于永磁同步电机的特征频率识别与高频边带噪声的主动控制优化。
1 边带电磁力特征分析
1.1 气隙磁场与边带电磁力解析
为分析永磁同步电机边带电磁力的时空特征,首先需要对气隙磁场进行分析。在永磁同步电机中,气隙磁场由转子永磁体场和定子电枢磁场组成,且作用在定子齿面上的电磁力是振动噪声的主要来源。忽略磁饱和效应,径向气隙磁通密度Bn可在定子坐标系下表示为:
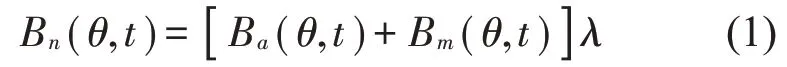
式中:Ba为径向电枢磁场;Bm为永磁体磁场;λ为考虑定子开槽作用的气隙相对磁导率。这3部分可以使用傅里叶级数分别表示为:

式中:v表示电枢磁场谐波阶次;θ为空间机械角度;p为极对数;z为槽数;Nt为电机极对数与槽数的最大公约数,即Nt=GCD(p,z),表示空间周期数;B0为基波电枢磁场;ω0为定子基波电流角频率;λ0为平均气隙磁导;Bh为谐波电枢磁场;ωh为谐波电流角频率;Bμ为永磁体磁场;μ为永磁体磁场谐波阶次,μ=2k-1(k=1,2,3…),由于永磁体基波磁场是振动的主要贡献量,因此有μ=1;η为齿谐波阶次。
根据麦克斯韦应力张量法,忽略切向气隙磁场的电磁力密度可表示为:

式中:μ0=4π×10-7为真空磁导率;Bt为切向气隙磁通密度,且Bn≪Bt。
将式(1)至式(4)代入式(5)中可以得到考虑电流谐波的径向电磁力密度解析表达式,进一步归纳出电磁力的空间阶次与频率分布特征如表1所示。其中,ω0=2πf0,f0为基波电流频率,且有f0=fr∙p,fr为电机转频;fh为谐波电流频率。
由表1 可以看出,谐波电枢磁场本身及其与永磁体磁场、基波电枢磁场间的相互作用都会产生边带电磁力。而基波电枢磁场幅值较小且不会引起额外的空间力谐波[15],为简化计算,可以忽略永磁体磁场与基波电枢磁场的相互作用及开槽的影响。因此,仅考虑永磁体磁场与谐波电枢磁场相互作用,对受载波频率影响的部分进行解析,将边带电磁力密度表示为:

表1 电磁力密度来源与时空特征

由此可知,不同于理想正弦电流下的力频率,考虑电流谐波的边带力频率为(μf0±fh)。因此,为解析SVPWM在载波频率附近引起的边带电磁力的时空特征,需要进一步分析不同电流谐波对边带电磁力与振动噪声的影响。
1.2 考虑电流谐波的边带电磁力时空特征
电磁力的时空特征因绕组类型与极槽组合的不同具有多样性。根据极槽组合,通常将永磁同步电机分为整数槽电机和分数槽电机。与整数槽电机相比,分数槽电机因其高效率、高转矩密度、端部绕组短等优点应用更加广泛,但其每极每相槽数为分数,导致电磁力的空间阶次较低,振动噪声问题更为突出[16]。常用的分数槽电机满足z0=2p0±1或z0=2p0±2,其中z0=z/Nt,p0=p/Nt。本文主要分析了z0=2p0±2的分数槽永磁同步电机边带电磁力的时空特征。
根据绕组对称性可知三相电机中不包含3及其整数倍谐波,且满足z0=2p0±2 的分数槽永磁同步电机中仅存在v=6k±1 次谐波。由文献[17],SVPWM引入的电流谐波由两部分组成:
(1)(6k±1)倍基频的谐波。如第5、7、11和13次谐波,此类谐波引起的径向力谐波频率为(6k±1)f0,耦合力频率μf0±fh=[μ+(6k±1)]f0。根据表1 可以看出,与理想正弦电流下的力频率相同,此类谐波产生的电磁力频率为基频的偶数倍。
(2)载波频率fc引起的边带电流谐波。以第一载波频率为例,其引起的边带电流谐波的频率可表示为fc±2kf0[4],进一步耦合得到的边带电磁力频率为fc±(2k±μ)f0。当只考虑永磁体基波磁场最大振幅即μ=1 时,力频率可表示为fc±(2k±1)f0。由此得出的边带电磁力频率特征如表2所示。
由于电机的振动噪声水平与电磁力空间阶次的四次方成反比[18],低空间阶次的电磁力对振动噪声起主导作用。因此仅对空间零阶和最低非零阶边带电磁力的时空特性进行解析。对于满足z0=2p0±2的分数槽永磁同步电机,其最低非零阶力的空间阶次为2Nt[7]。
根据表1与式(6),0阶边带电磁力满足:

对于电流谐波fh=fc+2f0,0阶边带电磁力的耦合频率可表示为:
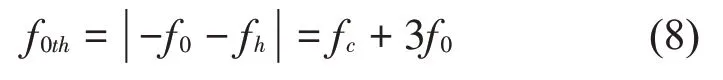
类似地,可以得到由不同电流谐波引起的边带电磁力的空间阶次与频率特征的对应关系,如表2所示。由此可对永磁同步电机振动噪声的阶次与频率特征进行分析识别。

表2 边带电磁力的空间阶次与频率特征
2 电磁振动响应分析
以一台3 kW 小型新能源车用永磁同步电机为研究对象,为解析其振动噪声特性,建立了电机的三维结构模型与考虑电流谐波的二维电磁分析模型,如图1 所示。电机为12 槽10 极分数槽双层集中绕组,主要参数如表3所示。
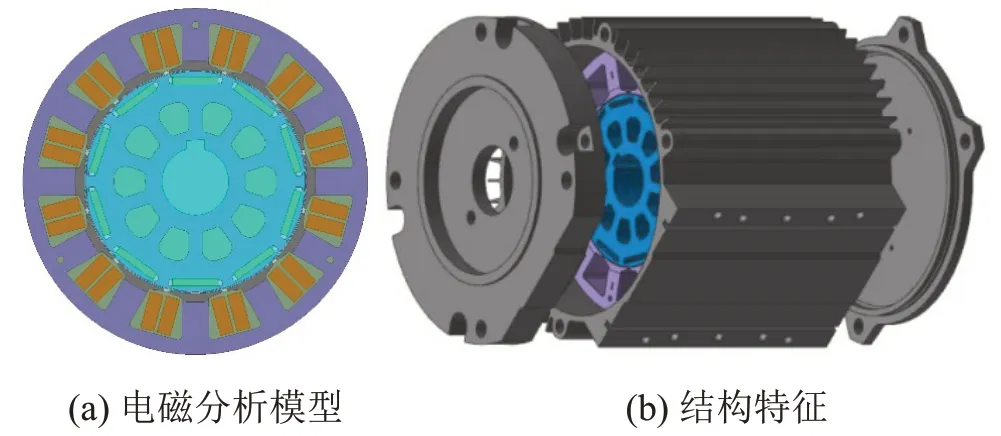
图1 永磁同步电机分析模型

表3 永磁同步电机的主要参数
采用SVPWM 策略对电机进行控制,设置载波频率fc为8 000 Hz。图2 为额定工况下根据仿真计算与试验采集得到的A 相电流频谱,其中电流基频f0为166.67 Hz。可以看出,虽然载波频率附近的电流谐波幅值相对较小,但具有明显的频率特征且与表2中得出的结论一致。此外,通过实测与仿真结果的对比表明了仿真计算的有效性,能够满足后续的电磁力分析。
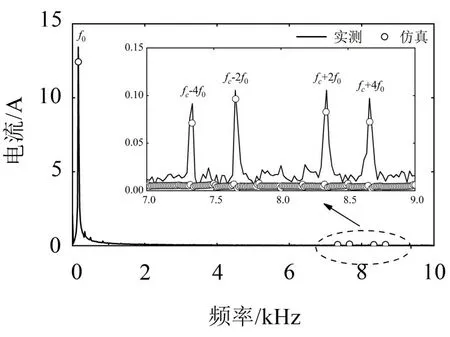
图2 额定工况下的相电流频谱
2.1 边带电磁力有限元分析
通过二维有限元分析计算气隙径向和切向磁通密度,如图3 所示。并通过傅里叶变换得到了磁通密度的谐波特征,见图4。可以看出,气隙磁密的切向分量较小,因此在分析过程中可以将其忽略。此外,该三相永磁同步电机采用双层集中式绕组连接,绕组节距为1,因此5次和7次谐波均受到了削弱。

图3 气隙磁密
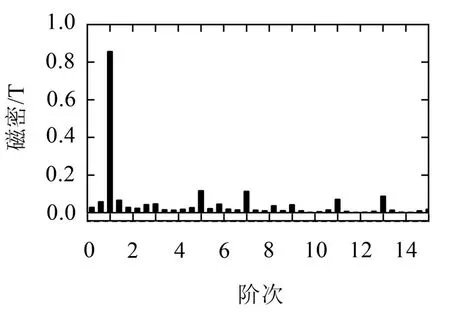
图4 径向磁密谐波成分
径向电磁力既是时间函数又是空间的函数,根据式(5)计算得到了转子旋转一周的电磁力密度,如图5所示。为得到边带电磁力的空间阶次与时间频率的对应关系,应采用二维快速傅里叶变换对径向电磁力进行时空分解。
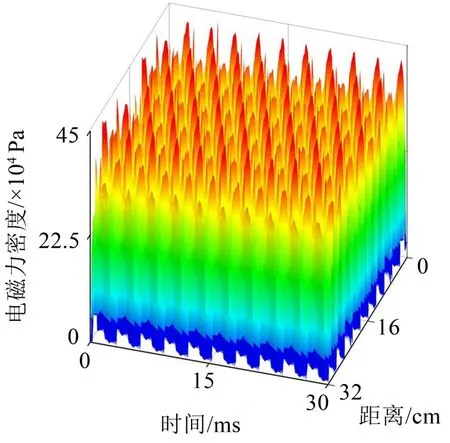
图5 额定工况下电磁力密度的时空分布
分解得到了基频整数倍电磁力及边带电磁力的时空频谱,如图6所示。其中,频率分辨率为电流基频,空间阶次的正负表示电磁力的方向。
由图6(a)可以看出,该频段内径向电磁力的频率表现为基频的偶数倍。其中(0,0f0)为直流分量,空间的-10 阶分量(-10,2f0)由永磁体基波相互作用引起,对振动噪声影响较大。图6(b)所示的边带电磁力时空分布特征与表2 中的结论基本一致。其中,2 阶边带电磁力主要表现在8 833 Hz(fc+5f0)与7 166 Hz(fc-5f0)处,0 阶边带电磁力的主要频率为8 500 Hz(fc+3f0)与7 500 Hz(fc-3f0)。
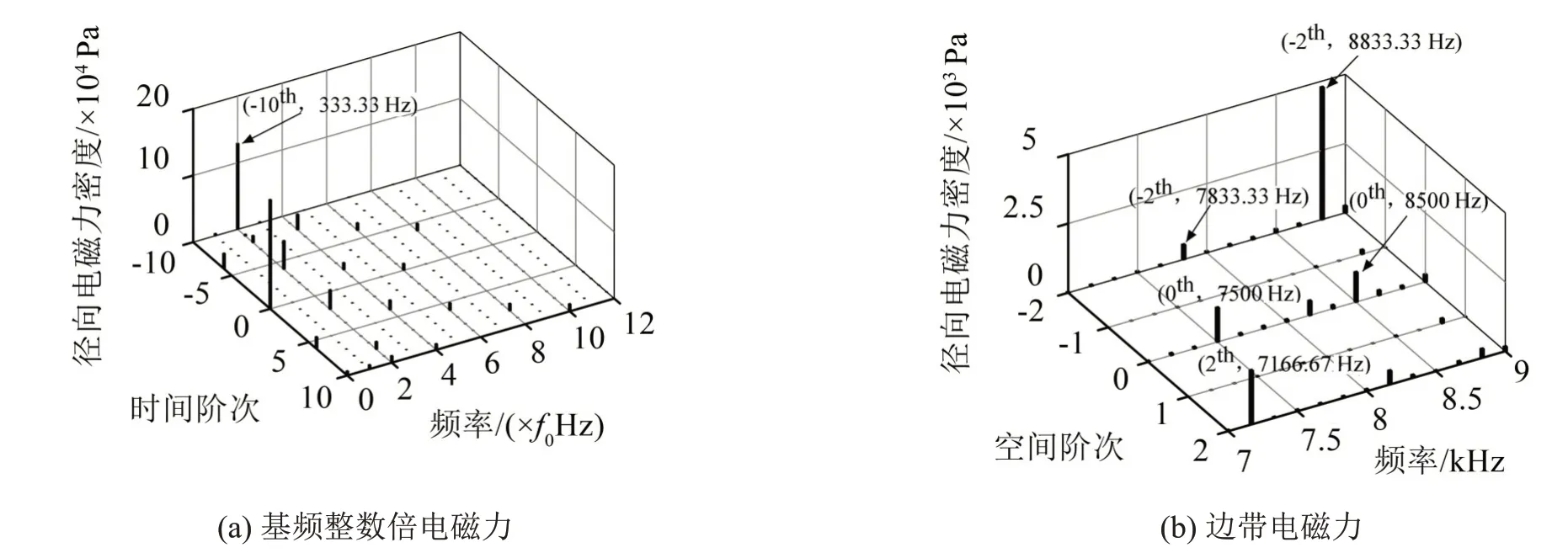
图6 电磁力的时空间分解
2.2 模态分析
为验证有限元模型的准确性并获取该永磁同步电机的模态参数,采用移动力锤法进行了模态测试,如图7 所示。样机在测试过程中使用弹性绳悬挂,共放置了5个加速度传感器以拾取结构表面的振动响应,同时选取了108个节点并对各节点进行3次敲击以提高锤击信号的相干性。表4对比了由仿真与试验所得的模态振型及频率,为更加直观地体现各阶振型,在结果中隐藏了前后端盖。结果表明,由仿真计算与实测所得各阶模态频率的相对误差均小于5%,验证了有限元模型的准确性。

图7 样机模态测试
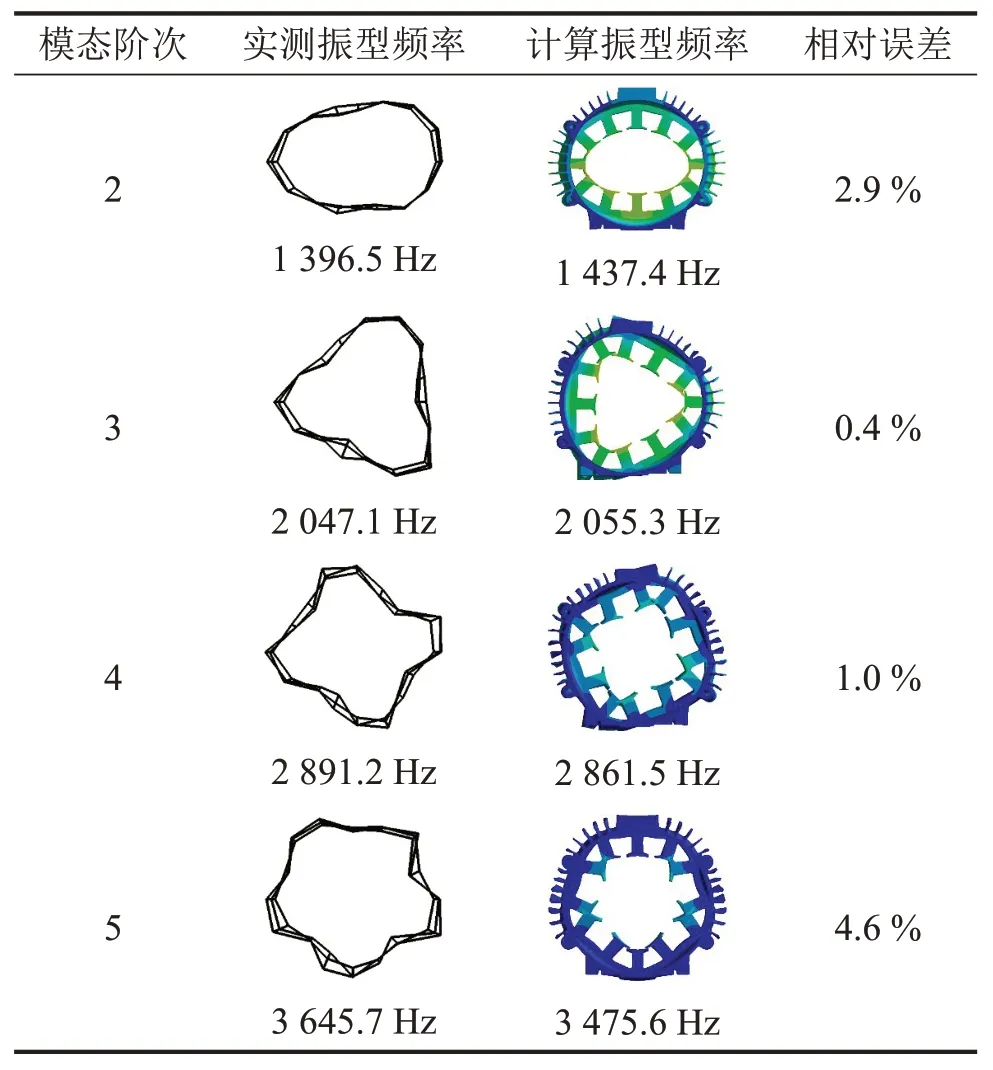
表4 仿真与实测所得各阶模态参数的对比
此外,电机的振动噪声与其结构特性密切相关,当电磁力频率接近结构固有频率时会引起共振,进而导致明显的振动噪声[19]。结合图6可以看出,低频部分的电磁力峰值出现在333.33 Hz,边带电磁力的幅值相对较小且峰值出现在8 833.33 Hz,与结构前5阶固有频率差距较大,由此可知电磁力不易引起该电机结构的共振。
2.3 振动响应
为计算样机的振动响应与电磁噪声,建立了如图8所示的多物理场耦合分析模型。
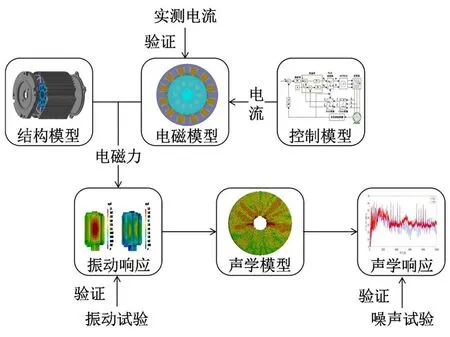
图8 永磁同步电机电磁噪声的多物理场分析流程
施加在定子内表面的电磁力是电磁振动噪声的主要来源。首先通过电机二维电磁模型计算定子齿内表面电磁力,根据结构的周期性,假设电磁力沿轴向均匀分布从而得到三维空间的节点力。进一步采用力插值法将节点电磁力施加到结构网格上作为振动响应分析的激励,图9 为作用在定子齿结构内表面网格上的节点力。
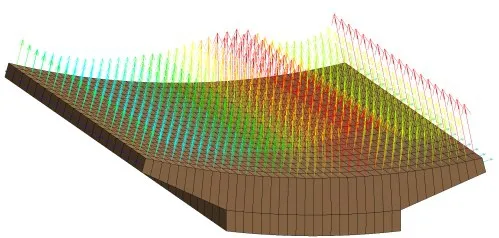
图9 齿面结构节点电磁力
基于模态叠加法,计算结构的振动响应[20]:
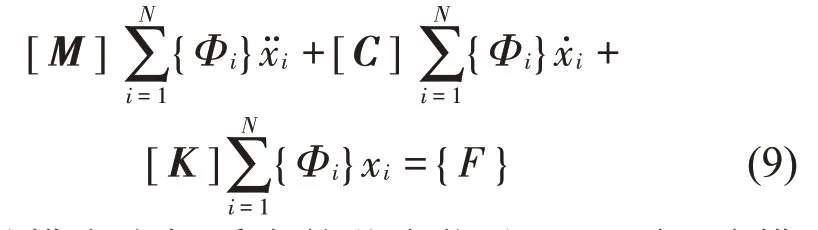
其中:xi是模态坐标系中的节点位移,{Φi}为i阶模态阵型,{F}是随时间变化的节点电磁力,N是叠加的模态阶次,[M]、[C]、[K]分别表示质量、阻尼和刚度矩阵。
图10 为额定工况下电机结构顶部中心点的振动加速度频谱,可以看出计算值与试验结果吻合较好。振动峰值出现在载波频率(8 000 Hz)附近,主要由边带电磁力引起。此外,受电机控制器和试验台架等非理想因素影响,实际电流信号中的谐波含量高于仿真电流,因此导致实测振动加速度数据相比有限元分析结果包含更多的谐波成分。
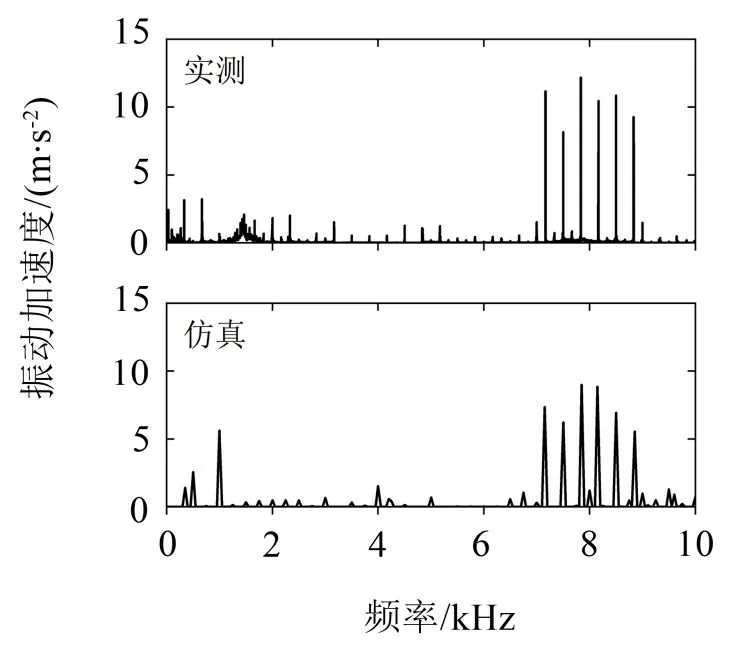
图10 额定工况下的振动试验与振动响应仿真结果
3 电磁噪声的预测与验证
基于振动响应分析结果,对电机的近场辐射噪声进行预测分析,并通过样机噪声试验验证仿真计算的准确性。图11为振动噪声试验台架,被测电机通过两个夹紧块及底部销孔定位并约束在台架上,经联轴器与磁粉测功机连接,并使用简易隔声罩隔离测功机与轴系的部分噪声。在试验过程中,使用Head SQuadriga II与LMS Test.Lab的多通道测试设备与分析系统以实现振动噪声数据的采集与实时处理。测试麦克风放置在距离电机壳体上方35 cm处,用于近场噪声的采集,声学传感器灵敏度为50 mV/Pa。

图11 电机振动噪声试验台
试验中采集了电机在2 000 r/min稳态工况下的振动噪声信号,并在LMS Test.Lab系统中进行频谱分析同,得到了电机在该转速下的A 计权声压级频谱。如图12 所示,通过对比分析电机在2 000 r/min下的近场噪声测试结果与仿真计算结果可以看出,由边带电磁力引起的噪声具有明显的频率特征,且峰值出现在8 500 Hz(fc+3f0)与7 166.67 Hz(fc-5f0),能够较好地反映特征频段的幅值与变化趋势。仿真结果与理论分析基本一致,表明基于多物理场耦合的分析方法能够满足永磁同步电机的电磁噪声计算要求。
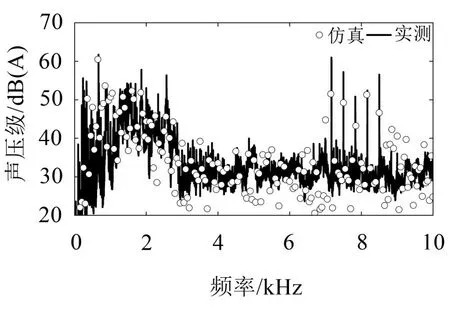
图12 电机近场噪声试验与仿真计算结果
此外,由于仿真分析中仅考虑了由电磁力引起的电磁振动噪声,而忽略了动偏心等装配制造误差产生的机械噪声与台架本身的影响,且实际控制器发出的电流信号谐波含量更加丰富,因此导致了部分频率的计算结果存在一定误差。
4 结语
本文对搭载SVPWM技术的永磁同步电机的边带电磁力特征及辐射噪声进行了研究。解析了考虑电流谐波的边带电磁力的频率与空间阶次特征,建立了包含电磁、结构及声学的多物理场耦合分析模型。对一台12 槽10 极永磁同步电机进行了电磁振动噪声有限元分析,并通过样机试验验证了理论分析及预测模型的准确性。研究结果表明:
(1)由载波频率引起的边带电磁力具有明显的空间阶次与频率特征,是电机高频电磁噪声的主要贡献量。
(2)建立的多物理场耦合模型能够有效地对永磁同步电机边带噪声进行预测分析。
本文的研究方法不仅可用于永磁同步电机边带电磁噪声的特征分析与识别,为电驱动系统在不同控制策略影响下的声振响应分析提供理论基础,同时有助于NVH 开发初期的噪声预测与主动控制策略优化。
