基于节点和链路容量的无线传感器网络级联故障研究∗
2021-12-15李英华梁
李英华梁 妍
(郑州工商学院,河南 郑州451400)
无线传感器网络(wireless sensor net works,WSN)是一种由大量传感器节点通过无线方式协作检测感知和处理各种环境信息的分布式网络系统。通常无线传感器网络(WSN)的运行环境多为无人值守模式,因此存在传感器节点能量耗尽、软硬件故障、故意攻击等风险[1-2]。传感器节点故障将导致最初集成的网络拓扑结构进行重新划分,并降低网络的覆盖范围,甚至可能导致整个网络瘫痪[3]。因此,如何建立高度抗毁性无线传感器网络是当前无线传感器网络研究的重点[4]。
现有的无线传感器网络抗毁性研究多从静态角度出发,研究移除点或边界对网络拓扑连通性与可用性的影响,并未考虑网络的动态过程。但在现实无线传感器网络中,网络拓扑结构的改变将会造成网络数据流的重新分配,导致网络通信负载发生动态变化。网络通信负载的更新可能由于过载而导致新的节点故障,从而触发新的级联故障。但当前无线传感器网络的级联故障模型主要侧重于节点容量对网络性能的研究,忽略了链路容量的影响,从而导致流量指标无法正确的反映无线传感器网络的汇聚特征[5-6]。
针对无线传感器网络级联故障的抗毁性,国内外众多学者开展了大量研究。文献[7]指出传感器节点的流量负载与节点程度有关,但是由于模型忽略了节点在网络流量中的作用,其不能正确反映无线传感器网络的流量特征。在实际的无线传感器网络中,每个数据包都会生成传感器节点,并最终聚集在接收节点上,这使得网络流量以汇聚特征得以表现。文献[8]指出当传感器节点超出其负载能力时将过载,但是由于模型没有考虑无线链路的容量,从而无法揭示无线传感器网络级联过程的本质现象。
在无线传感器网络级联故障研究方面,文献[9]提出了一种负载-容量模型,该模型定义每个节点均拥有一定容量并承担相关负载,当节点发生失效行为时,该节点所承担的负载按照预设规则转移至网络中剩余其他节点,而其他节点也将可能因负载超出自身容量而导致失效,并引发新一轮的负载转移,后续诸如CASCADE模型、OPA模型、DC-Flow模型和RENEW模型等均是在负载-容量模型基础之上发展而来的。现实世界中,不同类型网络所对应的级联故障情形各不相同,研究表明输配电网络、物流保障网络、交通网络及因特网等均具有明显的级联失效特征且彼此间具有明显的差异性。文献[10]根据节点可变负载与恒定容量等特点,针对WSN无标度拓扑展开研究,得到度分布指数和幂律系数与WSN容错性能呈正相关;文献[11]则在此研究基础上,借助概率母函数法求解WSN无标度拓扑级联失效的临界负载值。尽管现有WSN级联失效研究取得了一定成果,然而在现实情形中,由于受网络规模和能耗限制,多数WSN均采用典型的分簇结构进行数据采集与传递,现有的WSN级联失效研究对于此类情况并不适用。
鉴于此,本文建立了一种受节点容量和链路容量限制的无线传感器网络级联故障模型,旨在通过构建网络级联抗毁性模型,使故障节点可在一定时间延迟后从故障状态恢复,从而提高网络稳定性。
1 问题描述
在不失一般性的前提下,提出了如图1所示的网络拓扑结构。由图1可知,该结构包括300个传感器节点,宿节点位于网络中心。在无线传感器网络中,传感器节点有两个任务:一是传输由自身创建的数据包,二是转发来自其他传感器节点的中继数据包,然后所有数据包最终聚集在宿节点。图2表示由LEACH生成的网络流量分布图,从图中可以看到接近宿节点的传感器节点具有更大的流量负载。图3表示由度和介数创建的网络流量分布图。

图1 参考的网络拓扑

图2 LEACH路由协议生成的网络流量的分布
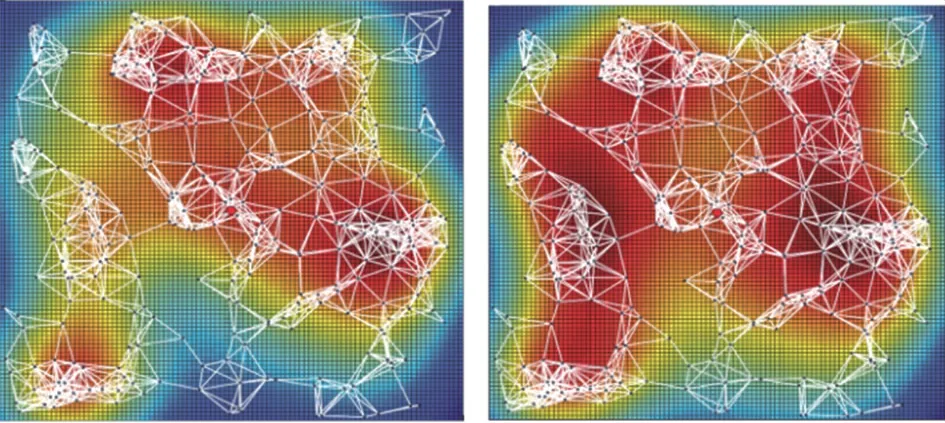
图3 网络流量分布图
如图3所示,为度和介数生成的网络流量分布图。其中,图3(a)中,传感器节点的连接越多,其负载往往越大,由此可知由节点度产生的流量分布只能反映邻近区域的流量交换;图3(b)中,在网络中每对传感器节点之间维持大量最短路径的节点,将承受更大负荷的网络负载。因此,在基于网际网络的负载模型中,仅假设数据包是从一个传感器节点,传递到另一个传感器节点,而不是从源传感器节点传递到宿节点。
此外,当前WSN级联故障模型仅考虑了节点的容量,没有考虑链路受限的情况,而节点到链路的容量因素也会对WSN流量分布产生重要影响。而现有模型过于简化了负载和容量,导致获得结果与实际偏差较大。另外,现有模型主要关注节点攻击引起的级联过程,实际上与由硬件故障引起的节点故障相比,WSN中的链路故障更常见。当发生链路故障时,链路负载将会重新分配,网络中的流量分配将得到更新,并且如果有任何传感器节点变为过载状态,级联故障将会继续,因此无线传感器网络的抗毁性评估是十分必要的。
2 方向介数原理
为正确反映WSN的流量特征,为WSN提出了一种新的流量度量“方向介数”,如式(1)所示[12]:
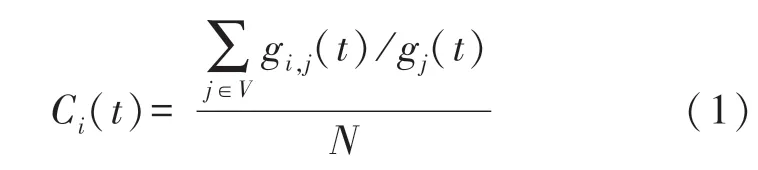
式中,gi,j(t)为在时间t经过节点i从节点j到宿节点的最短路径数;gj(t)为在时间t从节点j到宿节点的最短路径数;V是除宿节点之外的节点集合;N是除宿节点以外的传感器节点数。其中,方向之间的最极端情况为,从任何传感器节点到宿节点的最短路径中每条路径都会经过节点i,此时Ci(t)将为最大值1。当节点i位于网络边界,且没有节点要求它中继数据包时,其承担的负载只是其自身生成的数据包,此时Ci(t)将为最小值1/N。传统的介数主要用来量化一个节点沿着其他两个节点之间的最短路径的桥接次数,而方向介数是用来量化一个节点沿着所有其他节点到接收器节点之间的最短路径桥接次数。
在不失一般性的前提下,选择WSN中最常用的网络结构,如图4所示。表1为图4中通过度、介数和方向介数来测量的网络通信量。由图4可知,在该网络拓扑中,每个节点都必须经过节点1才能到达宿节点。因此,可以合理地认为整个网络流量将通过节点1。除了自行生成的数据包外,还需要节点2和节点3分别中继来自5个节点的数据包。由此可知,几乎有一半的网络流量将通过节点2和节点3,而其余传感器节点不承担任何中继任务,且其承担的唯一负载是自身负载。根据表1可知,方向介数完美地描述了上述流量分配功能,而度和介数都无法反映这一特征。
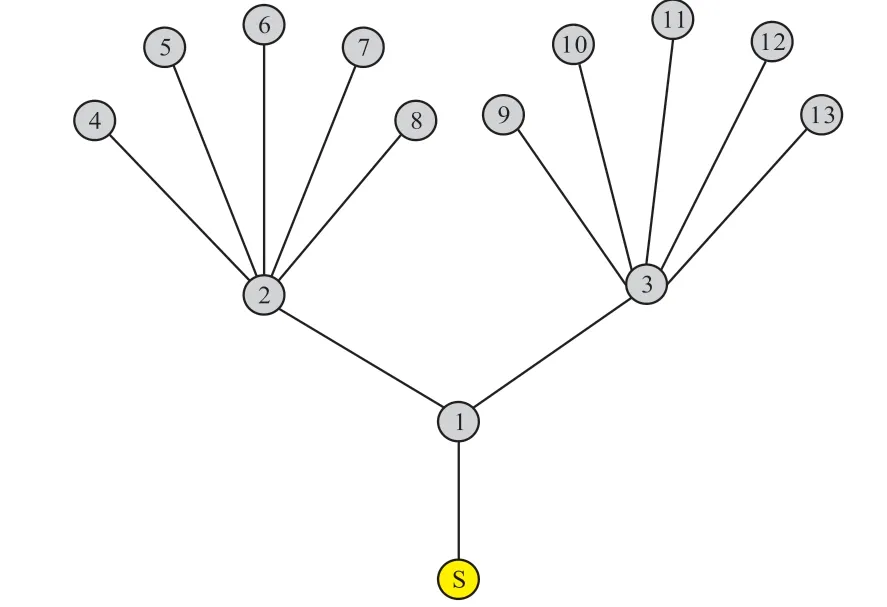
图4 WSN集群结构示例图

表1 网络流量分布表
如图5所示,为通过方向介数创建的网络流量的分布图。由图可知,WSN中的汇聚收敛功能与图2中的流量分布非常相似,表明无线传感器网络方向之间的合理性得到进一步验证。
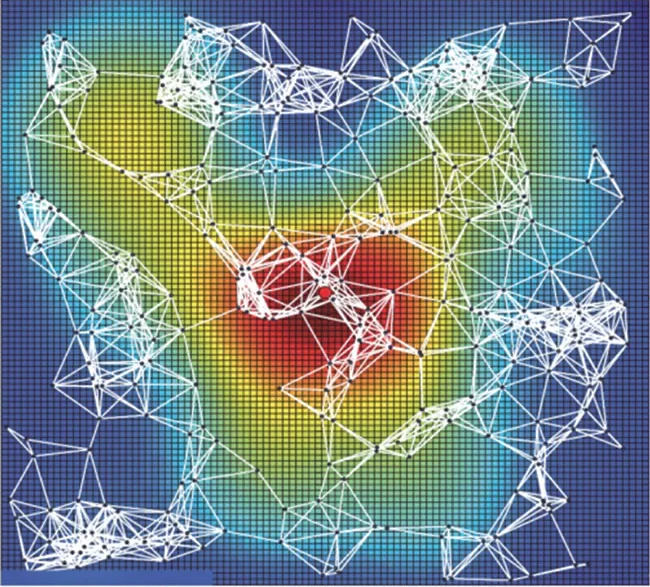
图5 方向介数产生的网络流量分布
3 WSN级联故障模型构建
3.1 网络假设
WSN可以用无向图G=(V,E)来描述,其中V={vi|i=1,2,…,N}是传感器节点的集合,而E={eij|i=j,vi∈V,vj∈V}是节点之间的无线链路的集合。如果节点i和节点j之间存在链接,则N×N邻阶矩阵[aij]的aij=1,否则aij=0。
在不失一般性的前提下,假设WSN中的所有传感器节点都具有同时生成和转发数据包的能力。每个传感器节点的数据处理能力取决于其缓存资源和带宽资源。他们在每个时间单位只能处理一定数量的数据包。如果节点缓存中的待办事项数据包超出了其数据处理能力,则在此时间单位无法处理的数据包将保留到下一个时间单位。
3.2 网络负载
在无线传感器网络中大多数的传感器节点具有多个链路,这意味着它们需要处理来自其相邻节点的多路径数据流量。根据数据流的方向可以将其分类为两种类型:输入数据流量和输出数据流量。以图4所示的流量分布图为例,节点2具有1、4、5、6、7和8六个相邻的节点,分别接收来自相邻节点4、5、6、7和8的流量负载De24、De25、De26、De27、De28。由于这些数据流量将输入到节点中2的缓存中,即定义为节点2的输入数据流量。节点2将流量负载De12传输到节点1,并最终传输到宿节点,即流量负载De12可定义为从节点2到节点1的输出数据流量,也可以定义为节点1的输入数据流量。通常情况下,总的输入流量负载和自身负载应等于输出流量负载,但是当网络拓扑结构更改后,输出流量可能会小于输入流量负载和自身负载。在这种情况下数据包无法及时得到传输并会堆积在缓存中,经过多轮数据积累后节点最终将过载。
为了清楚地描述WSN的级联过程,节点i在时间t的负载Li(t)如式(2)~式(6)所示[13]:
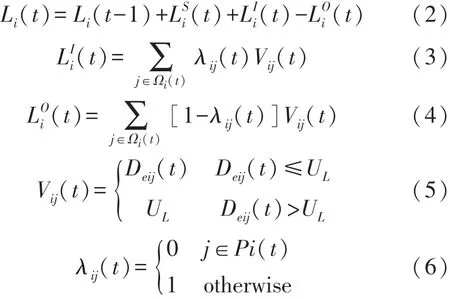
3.3 网络容量
节点的容量与初始负载呈正相关关系,如式(7)所示[14-15]:
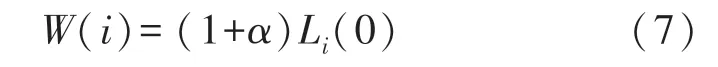
式中,α表示过载公差系数,Li(0)表示节点i的初始负载。但是在WSN中该设置与实际情况相差很大,出现这种情况,一方面是由于大多数情况下相同传感器网络的节点硬件配置是相同的,另一方面是由于在部署了数百甚至数千个传感器节点时无法自定义节点的容量。链路容量是影响WSN级联过程的关键因素,并且现有的所有研究都没有考虑WSN中链路容量因素的影响。本文利用方向介数来度量链路容量,结合式(1)和式(7)将链路容量UL定义为式(8)所示,其中Dejk(0)为ejk在初始时间处的方向介数;λl为链路公差系数。此时网络的初始方向介数的负载可由初始时间处的链路容量表示,如式(9)所示,其中λn为节点公差系数;
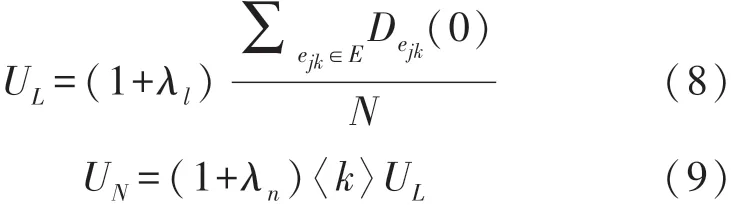
从式(8)和式(9)可以看出,每个传感器节点具有相同的链路容量和节点容量,且与初始方向介数的平均负载呈正相关关系。
3.4 级联机制
现有级联故障模型中,传感器节点具有正常和过载两种状态。对于WSN而言,当流量负载足够大时,越来越多的数据包将无法及时传递,并且随着时间的推移会在许多中央节点上进行积累,从而出现网络拥塞。网络拥塞是由于网络中的路由节点负载过度,导致网络性能下降,并且是网络处于持续过载的状态。因为无线传感器网络是分组交换网络,所以上述定义在无线传感器网络中也适用。如图6所示为网络拥塞图,当网络负载较低时,网络中传输的分组与网络发送分组成正比,这时网络时延最小。随着网络负载的增加,网络中传感器节点不能及时将分组转发出去,导致网络的丢包率增加、吞吐量下降和分组的时延变大。当无线传感器网络的负载量超过网络的处理能力时,导致数据包丢失、网络吞吐量下降,并增加时延。和传统有线网络、无线网络一样,无线传感器网络发生拥塞以后也会导致网络性能下降,无法保证无线传感器网络的服务质量。
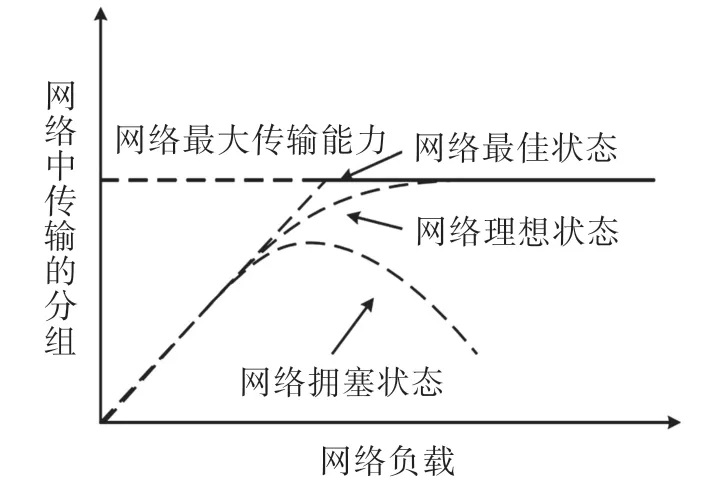
图6 网络拥塞图
在本文模型中,针对WSN网络拥塞,需要首先为每个传感器节点定义一个拥塞函数,如式(10)所示:
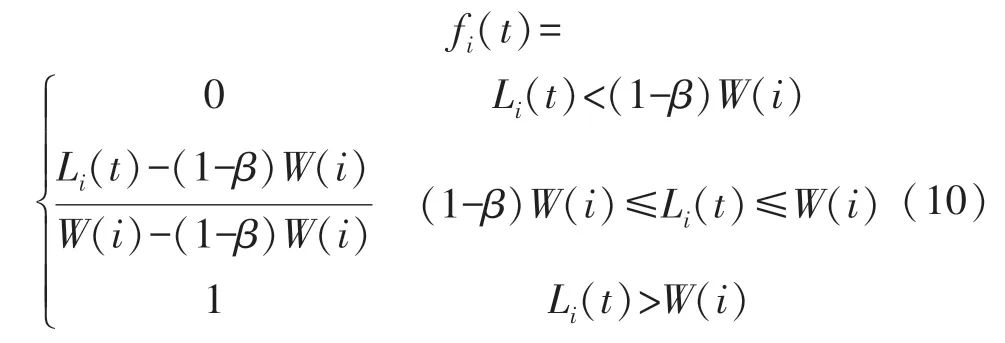
式中,β是拥塞的容忍系数,表示正常状态和拥塞状态间的调整阈值,其值与传感器节点的资源有关。
当Li(t)<(1-β)W(i)时,该节点处于正常状态,表明传感器可以正常工作。当Li(t)处于[(1-β)W(i),W(i)]范围内时,该节点处于拥塞状态,表明传感器仍可以接收和发送数据包,但其处理能力将会相应减弱。当Li(t)>W(i),该节点处于过载状态,表明该节点暂时无法运行。在该状态下,节点将被赋予恢复时间Δt。
在Δt时间内,该节点无法接收、处理和传输数据包,且缓存中的现有数据包也将被清除。当Δt过期时,该节点将再次变为正常状态。实际上,可以将t视为过载节点,并重新启动所需的时间。在实际的WSN中,传感器节点将在过载时重新启动而不是永久删除,且缓存也将被清除。重新启动完成后,传感器节点将加入网络并正常运行,对无线传感器网络的级联过程具有重大影响。当Δt接近0时,表明过载节点可以立即恢复,因此由过载引起的损害将最小化;若Δt接近∞,则所提级联方案等效于传统的永久删除方案。若节点的所有邻居都过载,即使其负载在容量范围内,由于该节点与宿节点之间的传递路径被切断,仍无法将数据包传输到宿节点,此时此类节点被称为隔离节点。当部分相邻节点从过载中恢复,并且到宿节点的有效路径出现时,隔离的节点可以被修复。如图7所示,为级联过程中传感器节点的状态转换图。

图7 级联过程中传感器节点的状态转换
3.5 拥塞感知路由恢复机制
根据本文的级联机制,过载的传感器节点可以通过重新启动进行自我恢复,但是重新启动后,如果仍然遵循最初的路由机制,它们将在一段时间后再次过载。因此有必要设计一种路由恢复机制来防止过载的节点不会进入“重启循环”状态。为了恢复故障节点,传统的模型通常选择拥塞值之和最小的链路,这些恢复解决方案只能在节点具有全局拥塞状态信息时有效。然而在无线传感器网络中,传感器节点以分布式方式组织,每个传感器节点不可能实时知道其他节点的拥塞状态。因此本文提出了一种局部拥塞感知的路由恢复机制,即当传感器节点正常工作时,会遵循原来的路由机制,当发生过载时,将遵循路由恢复机制。在这个机制中每个传感器均有一个Ui(t),表示如下:

式中,di(t)表示节点i在时间t的深度,当传感器节点需要转发中继数据包时,它将从相邻节点中选择最大的Ui(t)节点作为下一个跃点。
4 实验结果与分析
4.1 抗毁性指标
本节定义的两个指标分别为网络效率Ug(t)和正常节点比例Hn(t)。在现有的在模型中,网络效率Ug定义为其中dij表示节点i和节点j之间的最短路径。但是该定义不能正确反映出无线传感器网络的汇聚特性。由于在传感器网络中用户更加关注普通传感器节点传递消息的效率,通常在传感器网络中,用户更加关注从公用传感器节点到接收器的消息传递效率。因此,网络效率Ug(t)是从任何传感器节点到宿节点的最短路径的效率的平均值,如式(12)所示:

式中,di(t)表示时间t内节点i到宿节点的最短路径数量。与大多数现有模型不同的是,本文所建立的方法将与宿节点保持有效连接的节点视为正常节点,正常节点的比例Hn(t)如式(13)所示:
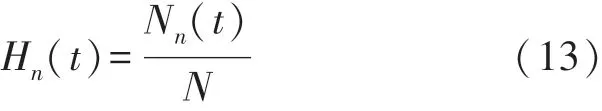
式中,Nn(t)表示时间t内的正常节点数量。在这里用Ug(∞)和Hn(∞)表示当网络发生级联故障后达到稳态时的网络效率和正常节点比例。
4.2 模拟设置
在大多数级联故障模型中,级联故障在传感器节点受到前q%的初始攻击时会被触发,然而与由硬件故障引起的节点故障相比,链路故障更可能是由于较少的无线传输引起的。
本文利用MATLAB 8.0进行了仿真模拟,建立的网络拓扑结构模型中有300个传感器节点,分布在300 m×300 m的区域。宿节点位于区域中心,无线传输半径设置为30 m,初始攻击设置为前10%的链路,为了确保级联故障是由故意攻击触发的,攻击之前假设初始网络中的每个节点都是正常的。
4.3 抗毁性指标分析
为了便于描述,分别使用GNE和GPNN表示常规网络效率和常规正常节点比例,使用NE和PNN表示本文提出的网络效率和正常节点比例。图8展示了四种网络拓扑情形。情形1表示初始拓扑结构没有节点故障,其他三种情形中存在一定数量的节点故障,四种情形的详细信息如表2所示。
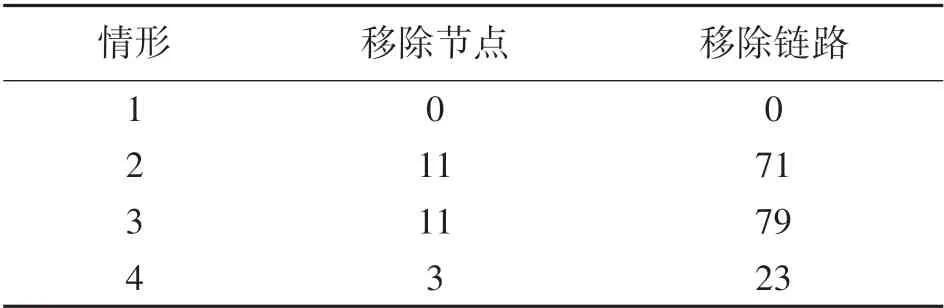
表2 4种情形的详细参数
从图8(a)中可以看出,由于没有节点故障第1种情形的网络连接是最优的。在图8(b)中,由于宿节点周围的节点发生故障,各个节点与宿节点之间的所有路径都被中断,导致传感器节点无法再将数据传递到宿节点,那么可以合理地假设网络完全瘫痪了。在图8(c)中,仍然有少量节点可以保持与宿节点的有效连接。在图8(d)中,尽管到宿节点的网络连接不受影响,但由于部分节点故障导致路由的传输成本和传输时间增加。(虚线圆节点是从网络中移除的节点)
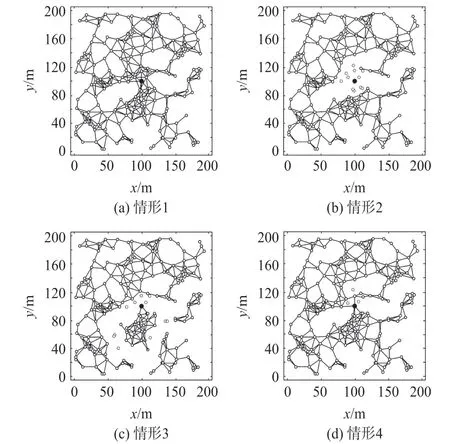
图8 四种网络拓扑结构
4.4 关键参数的影响
4.4.1 链路公差系数λl的影响
图9表示链路公差系数λl变化下正常节点Hn(t)的比例。从图中可以看出随着λl的增大,Hn(t)显著增加,当λl=0.5时,网络在t=5时达到稳态,且只有22%的传感器节点能够存活。当λl增加到2时,网络在t=1时达到稳定状态,83%的传感器节点能够存活。显然λl越高,传感器节点传输数据包的容量越大,流量负载不会堆积在缓存中,过载风险就可以得到显著缓解。

图9 λl变化下正常节点的比例(λn=0.5,Δt=∞)
图10 表示当级联过程达到稳态时异常节点的组成。从图中可以看出随着λl的增大,过载节点的比例将显著下降。当λl=0.5时,可以看到62%的节点因“被隔离”而不能正常工作。相比之下只有16%节点过载时处于故障状态。当λl=2时,被隔离是导致节点故障的唯一原因。此时链路容量只有足够强大应对蓄意攻击造成的流量变化时,级联过程才不会被触发。这也解释了为什么当λl=2的网络在t=1时能够达到稳态,即可以得出λl有一个可使网络不受级联故障影响的阈值。

图10 λl变化下异常节点的组成(λn=0.5,Δt=∞)
如图11所示,随着λl的增大,网络效率Ug(t)将显著提高。当λl=0.5时,Ug(t)将会稳定在0.012左右,这意味着信息传递严重延迟。当λl增大到2时,Ug(t)将稳定在0.123左右。此时大多数路由都可以生存,网络效率仍然可以得到保证,这是因为λl越高,生存节点越多,更多的路由被保留而不是被切断了。
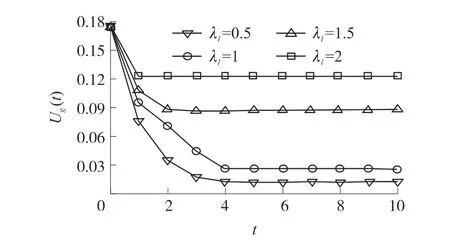
图11 λl变化下的网络效率(λn=0.5,Δt=∞)
4.4.2 节点公差系数λn的影响
图12表示节点公差系数λn变化下正常节点Hn(t)的比例。从图中可以看出λn的增大不能降低由级联故障引起的损害程度,但它可以推迟级联过程发生。当λn=0.5时,将在下一步攻击之后触发级联过程;当λn增大到2时,级联过程将从t=4开始;λn越大,缓存资源的改善越明显,但当输出流量超过带宽容量时,不能缓解数据包的堆积,当数据包发生堆积时,节点将在某些一时刻产生过载。
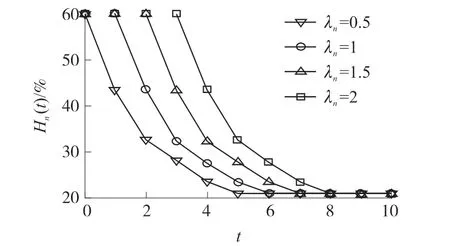
图12 λn变化下正常节点的比例(λn=0.5,Δt=∞)
如图13所示,λn的增加只会推迟级联过程中,不能改善级联网络故障的抗毁性。由于λn的增加无法将更多传感器节点从故障状态中解救出来,消息传递路径不会加强,因此网络效率将保持不变。

图13 λn变化下的网络效率(λn=0.5,Δt=∞)
本文模型中λn主要表示传感器节点具有缓存资源。因此当传感器节点不能从超负荷(Δt=∞)中恢复时,提供更多的缓存资源也无法对级联故障产生有益作用。
4.4.3λn和λl之间的关系
如图14所示,随着λl的增加,网络传输从低Hn(∞)阶段(左侧)过渡到高Hn(∞)阶段(右侧),相变的阈值λl∗大约为1.7。因此为了设计抗毁性优异的级联网络,λl应尽可能设置接近于阈值λl∗。当的值过大时将导致带宽资源的浪费,而当λl∗的值过小时级联网络的抗毁性较差。此外当Δt=∞时,网络的抗毁性不随λn的增加而有所改善。
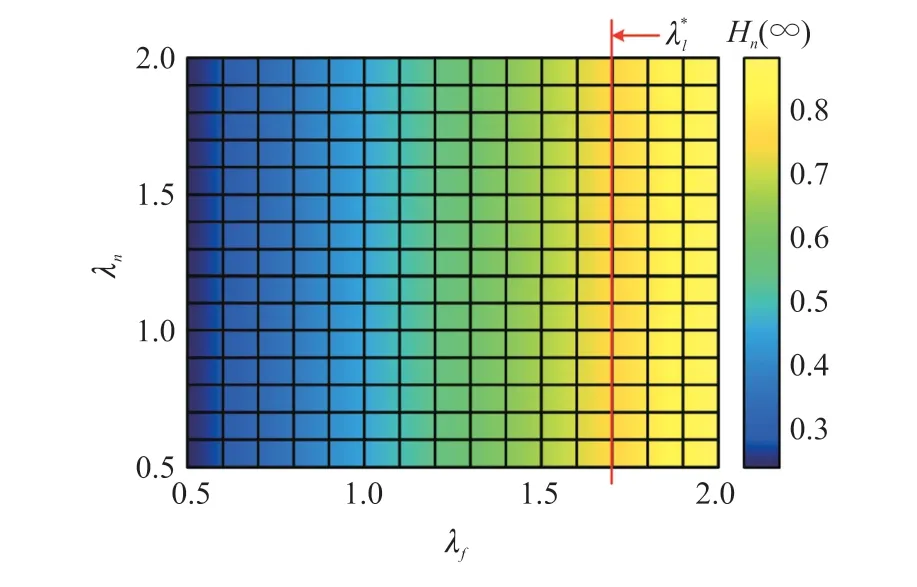
图14 [λn,λl]参数空间内的Hn(∞)波动图
如图15所示,随着λl的增大,网络传输从低Ug(∞)阶段(左侧)到高Ug(∞)阶段(右侧),相变的阈值仍为1.7。

图15 [λn,λl]参数空间内的Ug(∞)波动图
4.4.4 恢复时间Δt的影响
图16表示恢复时间Δt对正常节点比例的影响。从图中可以看出,随着时间Δt的增加,Hn(t)的推移波动加大。当Δt=1时,传感器节点可以在下一时间从故障中恢复,因此Hn(t)波动较为平缓,当Δt=3时,Hn(t)波动程度高于35%,当Δt=∞时,传感器节点失去恢复能力,Hn(t)将为一个稳态值。

图16 Δt变化下正常节点的比例(λn=λl=0.5)
如图17所示,类似于Δt对Hn(t)的影响,随着Δt的增加,Ug(t)的波动水平加大,当Δt=1时,Ug(t)约为0.06,当Δt增加到3时,Ug(t)在[0.021,0.065]之间,当Δt=∞时,Ug(t)单调递减稳定在0.012左右。
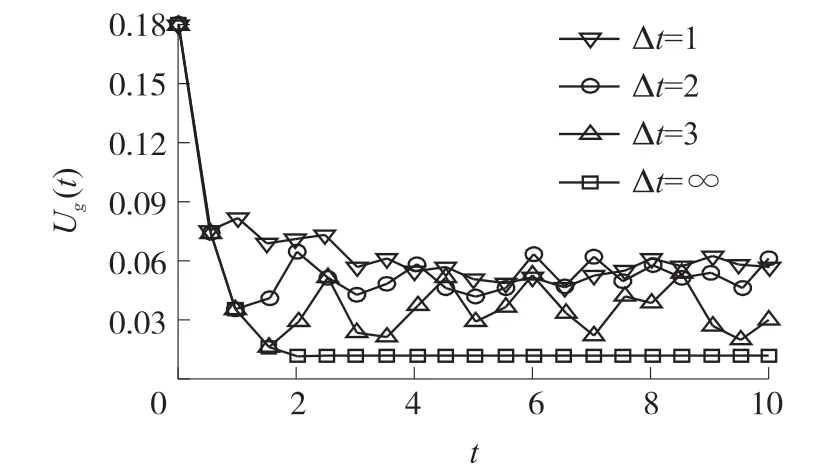
图17 Δt变化下的网络效率(λn=λl=0.5)
4.4.5λn和Δt之间的关系
当Δt=∞时(即节点不能从过载中恢复),节点容忍系数λn只能延迟级联过程发生,不能减少级联故障造成的损失。但是如果允许过载节点在一定的时间内发生延迟,λn的影响也会发生变化。
如图18所示,当传感器节点可恢复时,λn的增加可以减少级联故障造成的损失,降低Hn(t)的波动水平。例如,在Δt=2时,λn=0.5时,Hn(t)的范围为[45%,68%],当λn增加到1时,Hn(t)的波动范围缩小到[54%,67%],如果λn继续增加到2,可以发现Hn(t)趋于稳定值67%,则可以得出λ∗n存在一个阈值。根据级联机制,对于一个传感器节点,如果输入数据流量和自身数据流量大于链路容量,则不是所有的数据包都能被处理,并且部分数据将堆积在缓存中,经过多次循环后节点将变为过载状态。并且一个传感器节点从正常状态切换到过载状态需要一个持续时间Δts。为了便于描述,本文定义了故障节点和受影响节点。故障节点指由于过载原因导致的节点失效,受影响节点指受其他故障节点影响的节点。则如果Δts≥Δt,当失效节点恢复时,受影响节点仍未过载,且级联故障不会进一步扩散;如果Δts<Δt,受影响的节点将在故障节点恢复之前过载,级联进程将继续下去,并将出现新一轮的级联故障。

图18 Δt和λn变化下正常节点比例
如图19所示,随着λn的增大,Hn(t)的波动水平趋于减小,当λn达到某一阈值λn∗时,Hn(t)达到稳定状态。此外,λn∗随延迟时间Δt的增加而增加,因此为了防止级联故障扩散,Δts需要变的更长,λn∗需要更大。
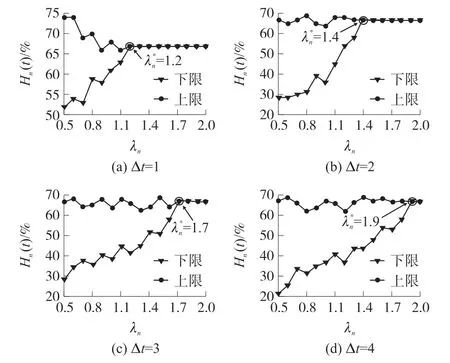
图19 Δt和λn变化下H n(t)的波动水平
4.5 对比实验分析
为了验证本文所提模型的有效性,选择了基于介数的模型和基于度的模型与本文所构建的模型进行了性能对比。模型中设置λn=λl=0.5,Δt=∞,由于这些模型使用不同的流量度量,触发条件也应该不同,为保证统一性,三种模型均按照前5%的节点攻击进行考虑。
如图20所示,在基于度的模型中级联故障造成的后果最严重,在t=5时89%的传感器节点进入故障状态。这是因为在基于度的模型中,流量负载使得级联故障更容易通过相邻节点进行传播。同时可以看出本文所构建的模型比基于介数的模型引发的故障更严重,基于介数的模型中有78%的节点可以存活,而本文所构建的模型中有71%的节点能够存活,仅略微少于基于介数的模型。另外,本文所构建的模型中,交通流量表示从任何传感器节点到宿节点的最短路径数,从而使数据流更多地集中在宿节点附近的关键节点上,当这些关键节点受到攻击时流量负载会发生变化,然后进一步导致更大规模的级联故障。
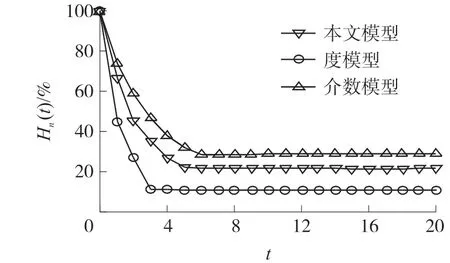
图20 三种模型的正常节点比例
图21表示当t=10时故障节点的组成。此时,三种模型的网络级联过程均能达到稳态。本文所构建的模型中节点的隔离主要由节点故障引起,在另外两个模型中,过载节点和隔离节点的故障相似。这是由于本文所构建的模型中,由于流量负载具有汇聚特性,重新分配的负载将更专注于宿节点附近的节点,一小部分过载节点会严重影响网络的连通性并会引起大量的传感器故障,从而形成隔离节点。
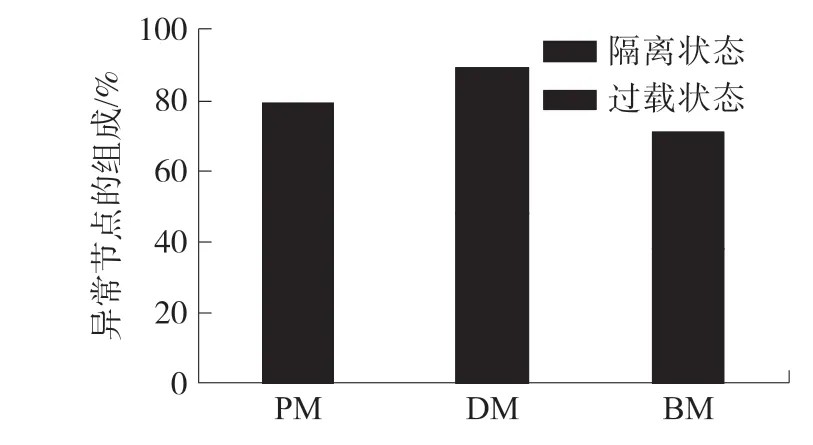
图21 t=10时故障节点的组成
4.6 路由恢复机制的性能
对于评估路由的恢复机制性能,本节设计了两种情况:①λl=λn=0.5,Δt=2;②λl=λn=0.5,Δt=∞。如图22所示,情形1中没有恢复机制,正常节点比例Hn(t)将在一段时间内减少到45%,然后在[45%,68%]之间波动。当引入恢复机制后,Hn(t)明显下降,并在一段时间内恢复达到100%。情形2中通过引入恢复机制,Hn(t)在t=5时即恢复到100%。同时从图23中可以看出,本文所提出的路由恢复性能在网络效率方面具有同样的优异性能。

图22 有/无恢复机制的正常节点比例
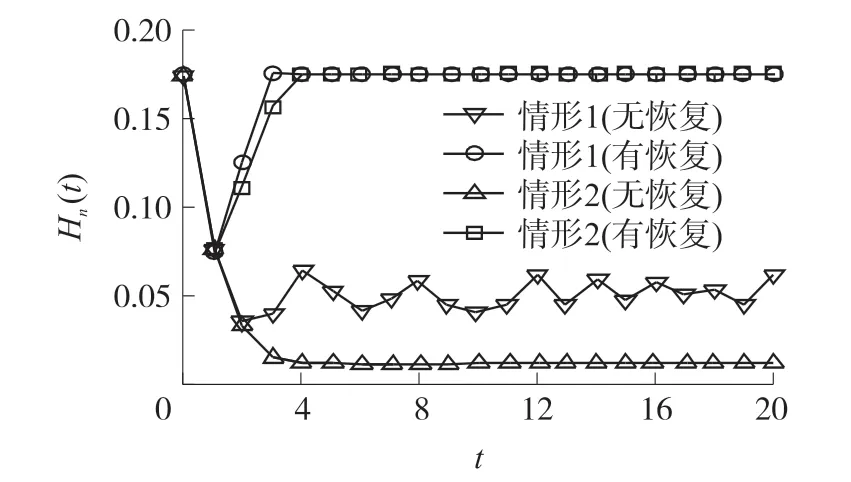
图23 有/无恢复机制的网络效率
5 结论
针对当前无线传感器网络的级联故障模型忽略了链路容量影响而导致流量指标无法正确的反映网络汇聚特征的问题,本文建立了一种受节点容量和链路容量限制的无线传感器网络级联故障模型。通过实验得到:①网络的无害性与链路容忍系数λl正相关;②在传感器节点不可恢复的情况(Δt=∞),节点容差系数λl的增加只能推迟级联过程,而不能减少级联故障所造成的损害;③恢复时间Δt的增加将加剧无线传感器网络中级联过程的波动水平。
