双十字轴对称式结构压磁式力传感器设计与研究∗
2021-12-15李瑞川丁馨铠徐继康孙会来刘继鲁谢玉东刘
李瑞川丁馨铠徐继康孙会来刘继鲁谢玉东刘 琦
(1.齐鲁工业大学(山东省科学院)机械与汽车工程学院,山东 济南250301;2.日照海卓液压有限公司,山东 日照276800;3.山东大学机械工程学院,山东 济南250100)
在现代农业机械中,大功率拖拉机应用广泛,随着拖拉机智能化要求不断提升,对其电液提升设备提出了更深层次的要求,早期采用高度调节方法,发展中逐渐出现了阻力调节、位置调节、力位综合调节等方法[1]。近些年,国外一些企业还采用了扭矩调节、压力调节、滑转率调节等方法,国内的研究主要集中在力为综合调节控制[2-6]。电液提升设备的性能直接影响到拖拉机作业质量及作业效率[7-8],其中力传感器是电液提升设备的重要部件,用于测量土壤阻力等外界作用力,其灵敏度直接影响到电液提升设备性能。
目前力传感器主要有压电式、电阻应变片式、压磁式,其中压磁式传感器结构简单、抗干扰能力强、灵敏度高、输出功率大广泛应用于大马力拖拉机电液提升设备中[9]。在国外,压磁式力传感器被应用于工业各领域[10-14]。但在国内,这种传感器核心部件大多依赖于进口,且结构过于单一,严重制约现代农业智能化发展,为缓解该局面,压磁式力传感器成为国内学者关注的重点[15-19]。
崔鑫鑫[20]等人使用片状铁钙合金和铁钴合金材料设计了一种力传感器,揭示了磁致伸缩力传感器的物理机制以及传感器输出特性的影响因素。翁玲[21]等人研究了偏置磁场对铁钙合金传感器性能的影响。王博文[22]等人通过研究铁镓合金的磁致伸缩特性,设计了一种基于Galfenol的新型磁致伸缩压力传感器,实现了压力的精准测量,分析了偏置条件、外压力等因素对输出电压峰值的影响。李鹏辉[23]等人对传感器磁路进行优化设计,提出了一种考虑材料本征非线性的磁路设计方法。上述研究主要集中在传感器材料以及影响输出特性的因素,但并未涉及传感器结构改进。本文针对现有的一种压磁式力传感器进行分析,指出了其结构上的不足之处,并在此基础上进行创新改进,提出了一种双十字轴对称式力传感器,对该传感器进行数学建模和磁路理论推导,并进行性能仿真分析和实验验证。
1 压磁式力传感器及其在拖拉机电液提升设备上的应用
压磁式力传感器是利用压磁效应来反映外界作用力的一种测力传感器,即当铁磁材料受力产生形变时,自身磁导率会发生变化,导致磁场发生变化[24-25],将磁场变化转化为输出电信号的变化,从而通过检测输出电信号的变化就可测得外界作用力的大小。压磁式力传感器一般安装在电液提升设备悬挂系统下拉杆的铰座孔中,承受下拉杆与支撑座之间的剪力,其外壳多为销轴式,受力区域为空心截面圆轴,结构紧凑,便于安装,并且空心截面具有较高的抗扭转、抗弯曲能力[26]。
目前在农用机械上应用范围比较多的是柱状力传感器,其结构如图1所示,当传感器受外力作用时,励磁磁芯的磁导率发生变化,在感应线圈上产生感应电压,进而导致差动连接后产生输出电压,该电压反映了外界作用力的大小。但是其励磁磁芯为柱状结构,决定了该传感器只可承受沿柱状磁芯一个方向上的作用力,研究表明,在农用机械实际工作中,往往不只受一个方向的作用力[27],这也使得该传感器灵敏度较差。励磁磁芯的安装位置应尽可能接近下拉杆剪切面处,但由于柱状力传感器只有一个励磁磁芯,使得该传感器只能检测一个剪切面处的外界作用力,在实际应用中,在外界载荷变化的情况下,剪切面往往不仅只有一个,这就使得传感器很难准确的反映作用力的大小。
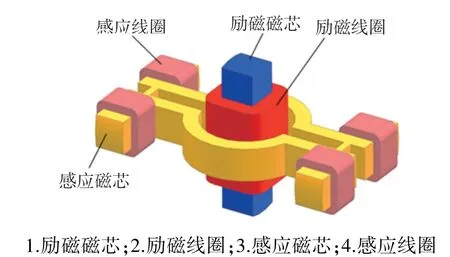
图1 柱状力传感器结构示意图
针对上述传感器的不足,本文提出了一种双十字轴对称式力传感器,结构如图2所示。此传感器由两个励磁磁芯和四个感应磁芯组成,每个励磁磁芯由两个励磁磁极垂直交叉组成,励磁磁芯和感应磁芯上分别安装有励磁线圈和感应线圈。由于两个励磁磁芯的存在,可同时检测多个剪切面处的作用力,且两个励磁磁极呈交叉布置,可同时承受沿两个励磁磁极方向上的作用力,即水平和竖直方向的作用力,可实现对两个方向上力的同时检测,产生的磁通量远大于柱状力传感器,使得磁场偏置程度进一步增大。在该结构中,将四个感应磁芯安装在励磁磁芯之间,使得各感应磁芯之间的距离缩小,大大减小了磁通量的外界损失。该传感器安装在承力筒内,励磁磁芯与承力筒内圆周面选用过盈配合,承力筒通过外圆周面上的插槽结构在下拉杆上定位安装。
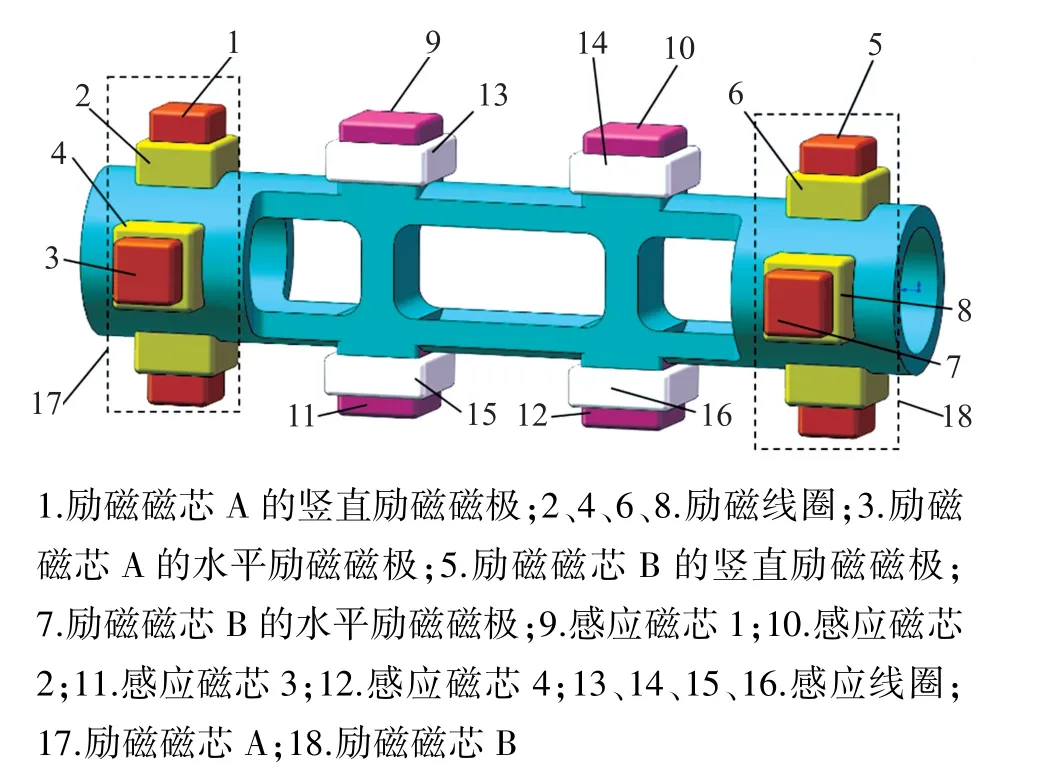
图2 双十字轴对称式力传感器结构示意图
2 双十字轴对称式力传感器磁路结构
2.1 传感器磁路结构基本要求
在传感器未受外界作用力时,输出电压的数值应尽可能为零,即传感器不能因为自身结构原因产生零点漂移现象,这是传感器的一个重要特性。对于双十字轴对称式力传感器来说,要求在传感器未受外界作用力时,通过感应线圈的净磁通量应为零,即水平和竖直方向的励磁磁芯产生的磁通量应为零或相互抵消。现分别推导水平和竖直两个方向上产生的磁通量情况。
2.2 水平磁路结构
根据图3可知,励磁磁芯A的水平励磁磁极和励磁磁芯B的水平励磁磁极产生的磁通量φAp和φBp分别流入四个感应磁芯,即

图3 励磁磁芯A的水平励磁磁极产生的磁通量流向示意图
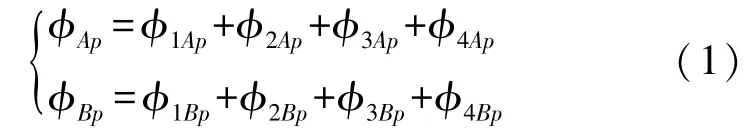
式中:φiAp和φiBp为由励磁磁芯A和B水平方向上的励磁磁极产生并流入到第i个感应磁芯的磁通量(i=1,2,3,4)。并可知,流入到感应磁芯i的磁通量φip为φiAp与φiBp的和,即:

在水平方向上磁路存在对称性,励磁磁芯A的水平励磁磁极到感应磁芯1和2的距离相等,即有φ1Ap=φ2Ap,到感应磁芯3和4的距离也相等,即有φ3Ap=φ4Ap。 同理可知φ1Bp=φ2Bp且φ3Bp=φ4Bp。
根据磁通量的连续性可知,进入到感应磁芯1的磁通量φ1Ap和φ1Bp在流出该磁芯后,将再分别流入其他三个感应磁芯,分别对应为φ1iAp和φ1iBp(i=2,3,4),即φ1Ap为φ12Ap、φ13Ap、φ14Ap三者之和。同理,φ1iBp为φ12Bp、φ13Bp、φ14Bp三者之和。对于感应磁芯1,流过该磁芯的磁通量有φ1Ap、φ1Bp、φ21Ap、φ31Ap、φ41Ap、φ21Bp、φ31Bp、φ41Bp,其中φ1Ap、φ1Bp为流入感应磁芯1,φ21Ap、φ31Ap、φ41Ap为由励磁磁芯A的水平励磁磁极产生并通过感应磁芯2、3、4后流向感应磁芯1的磁通量,方向为流出感应磁芯1,φ21Bp、φ31Bp、φ41Bp为由励磁磁芯B的水平励磁磁极产生并通过感应磁芯2、3、4后流向感应磁芯1的磁通量,方向为流出感应磁芯1,则感应磁芯1的净磁通量φ10p为所有磁通量的代数和,同理,也可得到各感应磁芯的净磁通量φi0p,即流入感应磁芯1的磁通量φ1p经过中间磁路传导,通过其他三个感应磁芯后返回励磁磁芯,构成完整地磁回路,等效磁路图如图4所示。
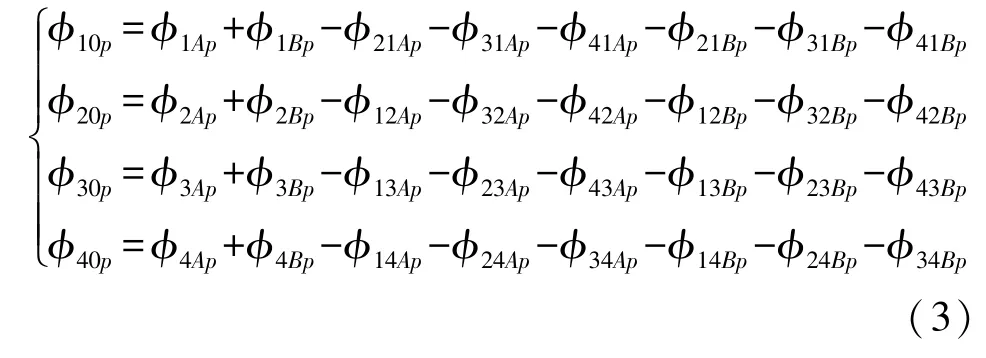

图4 φ1p的等效磁路示意图
并根据磁路的欧姆定律可知,磁路的磁通量为磁路磁动势Ep与磁阻Fs1的比值。由于水平方向方向的励磁线圈串联连接,可知该磁路磁动势Ep为励磁磁芯A的水平励磁磁极产生的磁动势EAp与励磁磁芯B的水平励磁磁极产生的磁动势EBp的和,且EAp与EBp均为励磁线圈匝数N与励磁电流I的乘积即NI,磁阻Fs1为上图中各磁阻的等效磁阻。由此可推导φ1p的表达式,即
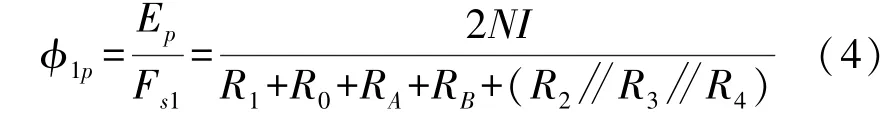
式中:Rn为第n个感应磁芯的磁阻(n=1,2,3,4),且四个感应磁芯的磁阻均相等。R0为磁路中其他部分的总磁阻,RA为励磁磁芯A的磁阻,RB为励磁磁芯B的磁阻,励磁磁芯磁阻为励磁磁芯等效长度l与励磁磁芯磁导率μ和励磁磁芯等效橫截面积s乘积的比值,即
同理可知:

根据式(5)可知,水平方向上流入四个感应磁芯的磁通量φ1p、φ2p、φ3p、φ4p均相等。即:

由于水平结构上具有对称性,其磁场也为对称分布,可知:
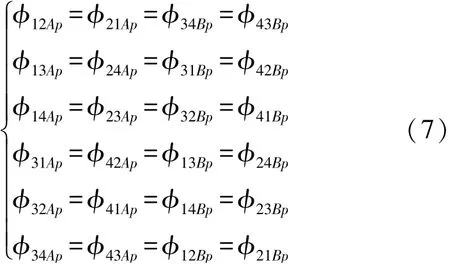
联立式(2)、式(3)、式(6)、式(7)得:

因此,在不受外力作用时,水平方向励磁磁场导致的各感应线圈输出电压Uip(i=1,2,3,4)为:
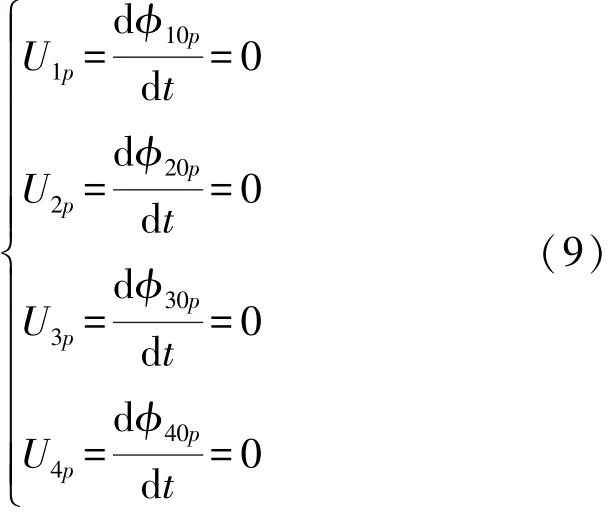
水平方向输出电压为四个感应线圈电压之和,即
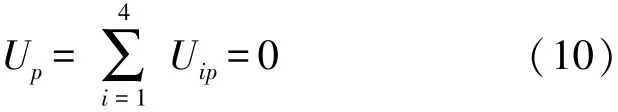
2.3 竖直磁路结构
由励磁磁芯A的竖直励磁磁极产生的磁通量如图5所示,由励磁磁芯B的竖直励磁磁极产生的磁通量和A相同。
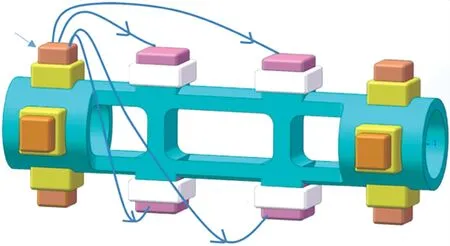
图5 励磁磁芯A的竖直励磁磁极产生的磁通量流向示意图
励磁磁芯A和B的励磁磁极的N极到感应磁芯1、3的距离比到感应磁芯2、4距离小,相应的磁路磁阻大小也不相同,所以有:
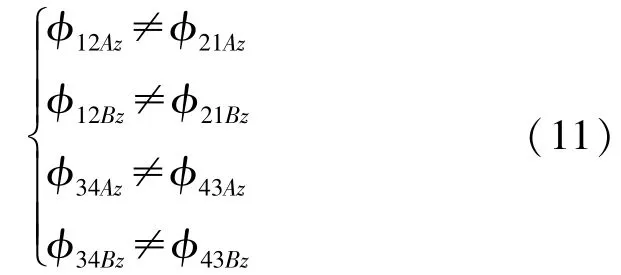
式中:φmniz为由励磁磁芯i的竖直励磁磁极产生并通过第m个感应磁芯后流向第n个感应磁芯的磁通量(m=1,2,3,4,n=1,2,3,4,i=A,B)。
由于在左右方向上传感器结构存在对称性,所以有:
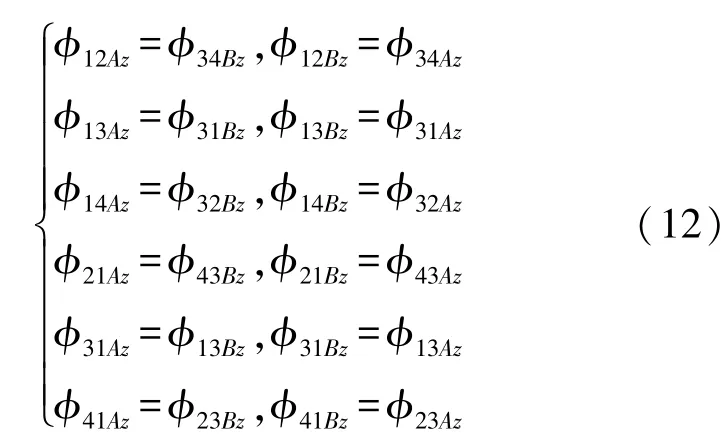
在竖直方向上流入每个感应磁芯的磁通量为:

在竖直方向上,对于感应磁芯1,φ1Az、φ1Bz为流入该磁芯,φ21Az、φ31Az、φ41Az、φ21Bz、φ31Bz、φ41Bz为流出该磁芯,则感应磁芯1的净磁通量为所有磁通量的代数和,并由此可知在竖直方向上各感应磁芯的净磁通量为:
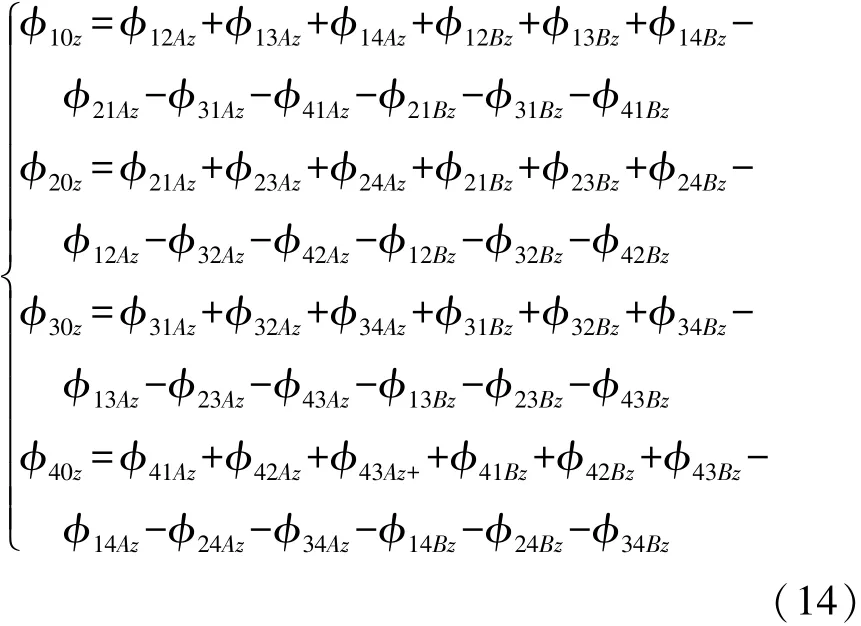
将式(12)代入式(14)可得

竖直方向上的输出电压为各线圈电压之和为:
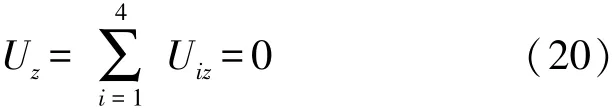
即竖直方向上各线圈输出电压虽然不为0,但是相互抵消了。
各感应线圈总输出电压Ui(i=1,2,3,4)为水平方向励磁磁场和竖直方向励磁磁场在各感应线圈上产生电压的代数和,且根据式(9)、(19)可知:
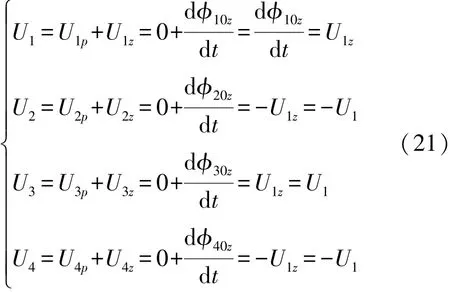
各线圈经差动连接后,总输出电压为:
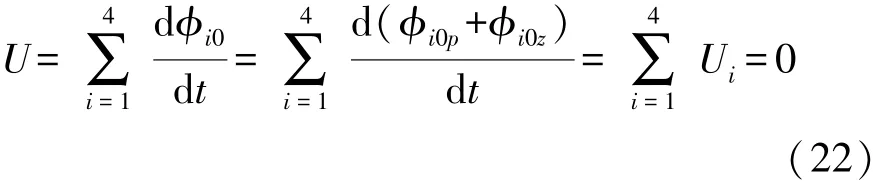
根据式(22)可知,各线圈经差动连接后,且在传感器不受外界作用力时,传感器输出电压为零,此公式证明了该传感器不存在由于结构变化而产生的零点漂移现象。
2.4 受外力作用时磁路情况
由励磁磁芯产生并流入各感应磁芯总的磁通量为水平方向和竖直方向的磁通量之和,在传感器未受外力作用时流入各感应磁芯的磁通量为
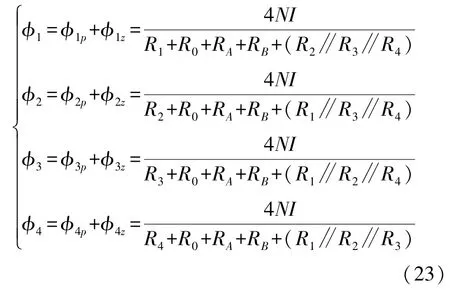
根据铁磁学原理可知,受外力作用时,各励磁磁芯不同方向上的磁导率发生变化,对应的磁阻也会发生变化,励磁磁芯产生并通过各感应磁芯总的磁通量变为φ′i(i=1,2,3,4):
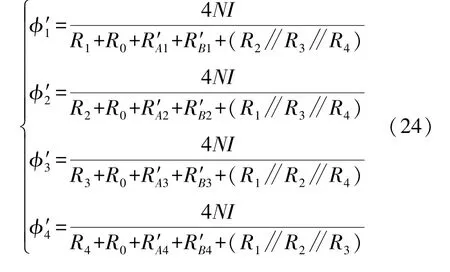
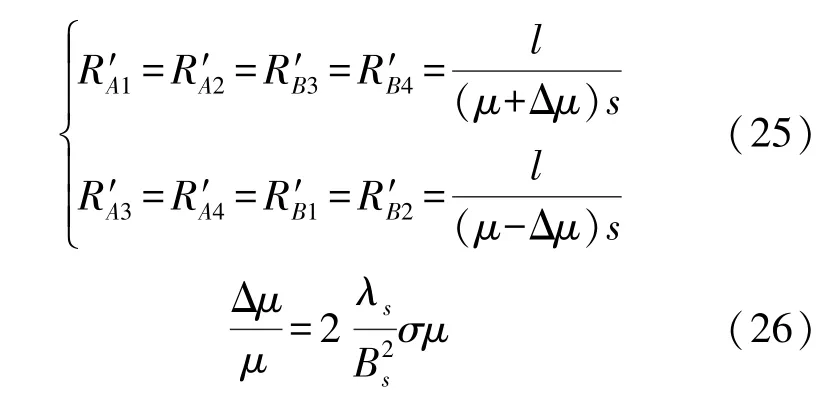
式中:Δμ为受力后励磁磁芯磁导率的变化量,λs为材料饱和磁致伸缩系数,Bs为材料饱和磁感应强度,σ为材料内部所受机械应力。
相应的φ′i0为:
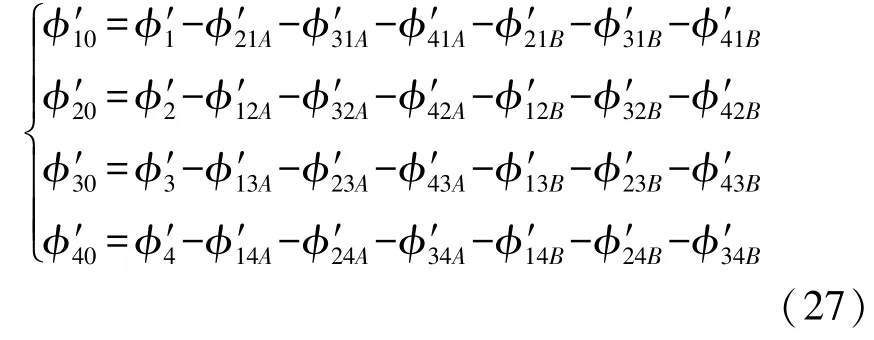
式中:
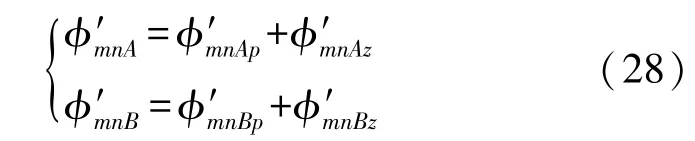
传感器受外力作用时,各感应线圈的输出电压为:
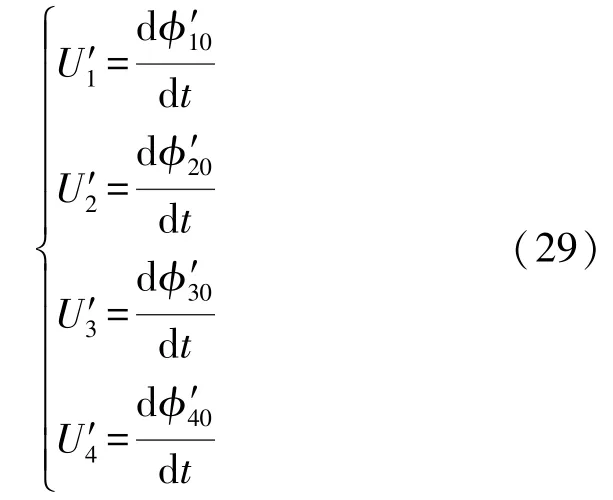
差动连接后总的输出电压为:

3 传感器仿真及实验分析
3.1 仿真与实验结果分析
根据上述公式推导,在MATLAB/Simulink中建立传感器仿真模型。并搭建力传感器测试平台对传感器的静态性能进行实验验证,该平台由双十字轴对称式力传感器、压力施加装置、数据采集装置和电脑组成,双十字轴对称式力传感器如图6所示。在水平和竖直方向上沿励磁磁芯轴线向双十字轴对称式力传感器施加的0~100 kN的力,每隔10 kN为一个测量点,同时为了保证数据的准确性,每个测试点进行5次测量,取5次测量结果的均方根值作为最终实验数据。

图6 双十字轴式力传感器
图7、图8分别表示传感器在受不同外界作用力各感应线圈电压和传感器输出电压情况。
在图7中可以看到,当外界作用力为0时,各感应线圈电压呈现周期分布,且感应线圈1和3的电压相同,感应线圈2和4的电压相同,这是因为水平方向上的励磁磁极在各感应线圈上产生的净磁通量满足式(8),即为零,从而水平方向励磁磁场导致的各感应线圈电压满足式(9),即为零。而竖直方向的励磁磁极在各感应线圈上产生的净磁通量满足式(18),即不为零,使得各感应线圈在竖直励磁磁极产生的磁场作用下发生式(19)的电压变化,从而在水平和竖直方向叠加后各感应线圈电压呈现与式(21)相同的变化,即表现为感应线圈1和3的电压相同,感应线圈2和4的电压相同。根据图8可知,双十字轴对称式力传感器在未受外界作用力时输出电压仿真结果最大值不超过1.3 mV,且输出电压经滤波处理后为零,实验得到的输出电压为零,这与式(22)也是相吻合的,结果证明了上文双十字轴对称式力传感器磁路推导的正确性。
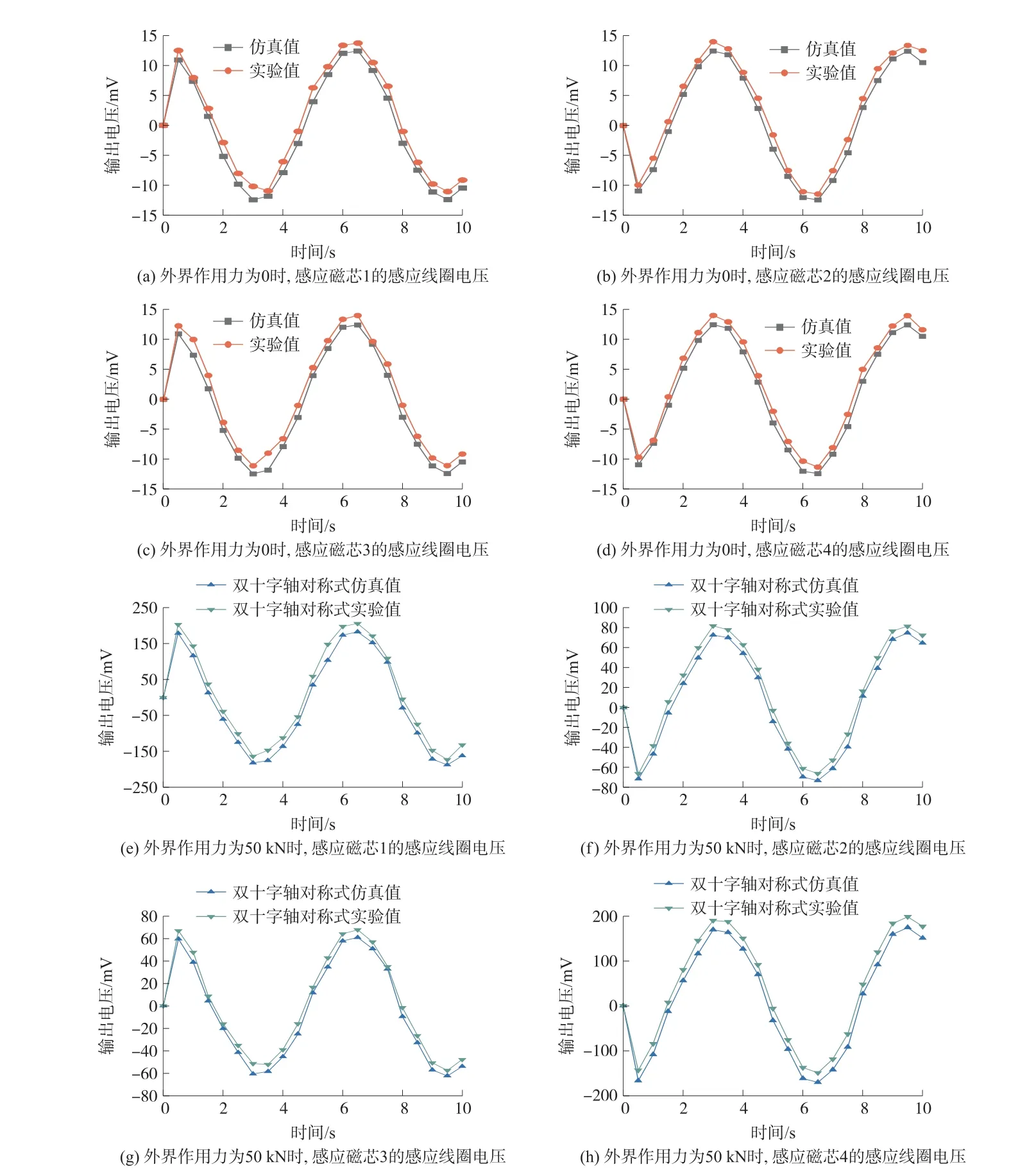
图7 不同外界作用力时,双十字轴对称式力传感器各感应线圈电压
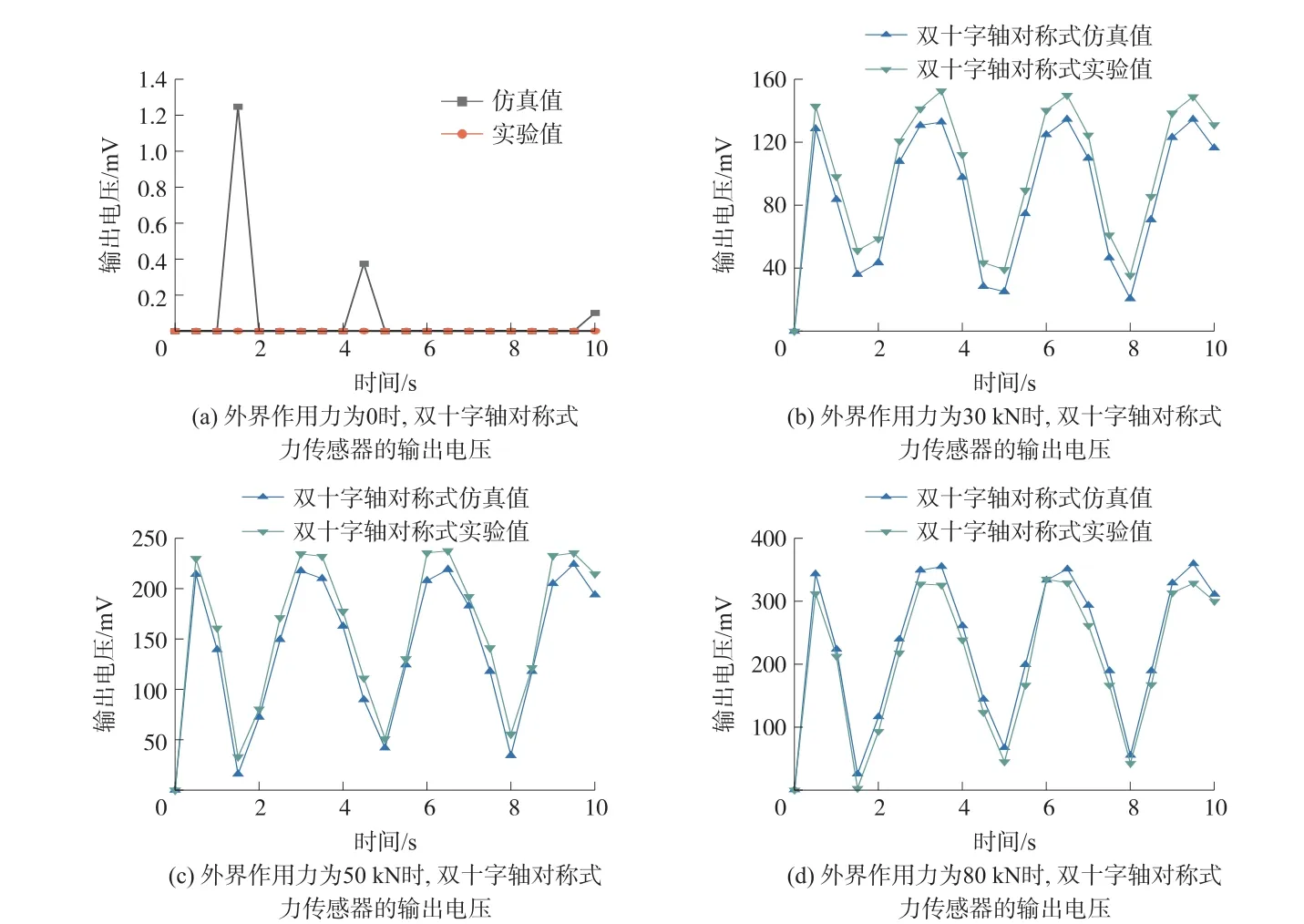
图8 不同外界作用力时,双十字轴对称式力传感器的输出电压
经实验测得传感器的外界作用力与输出电压关系,如表1所示,将各传感器在不同外界作用力作用下的电压输出数值进行拟合,得出传感器输出特性曲线,如图9所示。双十字轴对称式力传感器实验曲线与仿真曲线基本保持一致,双十字轴对称式力传感器输出电压远大于柱状力传感器,这是由于双十字轴对称式力传感器励磁磁芯数量大于柱状力传感器,可同时检测多个剪切面受力情况,并产生较大的磁通量,从而加大了磁场偏置程度,且由于励磁磁芯是由两个呈交叉分布的励磁磁极构成,可同时承受水平和竖直方向上的作用力,即同时检测两个方向上的作用力,使得磁场偏置程度进一步增加。在承受不同作用力时,双十字轴对称式力传感器输出电压的峰值是柱状力传感器峰值的三倍之多,这证明了该改进结构使得磁场偏置程度增大明显,仿真和实验得到的数值也符合式(23)~式(30)。
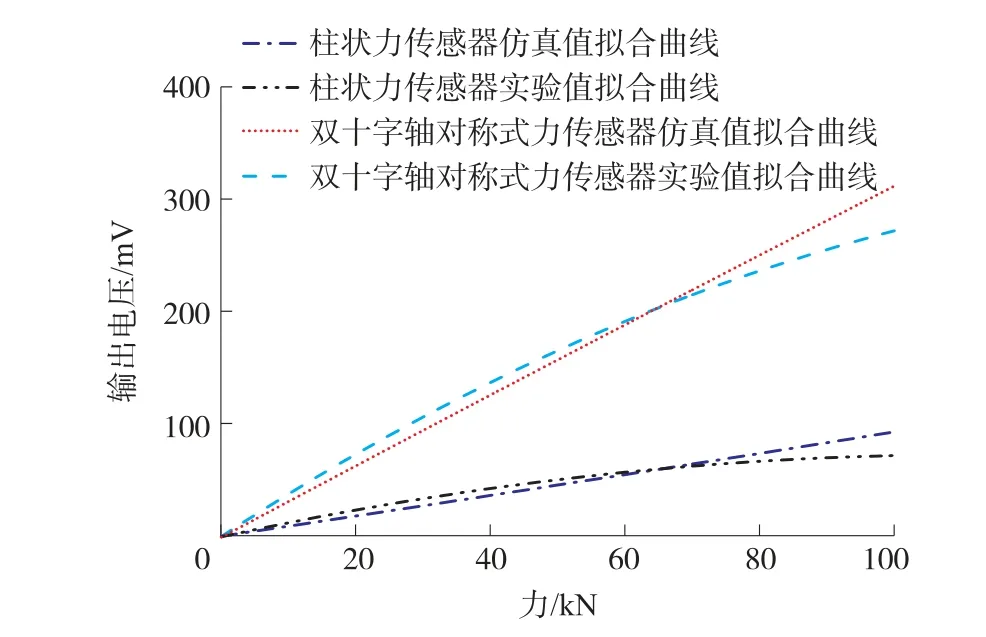
图9 传感器输出特性曲线

表1 两种传感器外界作用力与输出电压关系
在外力为30~80 kN的范围内双十字轴对称式力传感器有较好的线性输出特性和较高的灵敏度,且拖拉机电液提升设备下拉杆位置实际受力数值在此范围内。在外力大于80 kN时传感器没有明显的饱和现象,灵敏度降低比较缓慢。柱状力传感器在30~60 kN范围内有较好的线性输出特性,但其灵敏度较低,且外力在大于70 kN时,灵敏度降低幅度较大,出现较为明显的饱和现象。对输出特性进行线性拟合,可以得到两个传感器的灵敏度,柱状力传感器的灵敏度为0.724 mV/kN,双十字轴对称式力传感器的灵敏度为2.732 mV/kN,双十字轴对称式力传感器的灵敏度相对于柱状力传感器有大幅提高,提高量为277.35%,结果验证了仿真和磁路推导的正确性,也证明了双十字轴对称式力传感器相对于柱状力传感器具有较高的灵敏度,且有较好的线性输出特性,不存在明显的饱和现象。
4 结论
本文分析了一种用于拖拉机电液提升设备的力传感器的优缺点,并针对这种力传感器的不足之处提出了改进方法,相应的提出了一种双十字轴对称式力传感器,由于两个励磁磁芯的存在,可同时检测多个剪切面处的作用力,且两个励磁磁极呈交叉布置,可同时承受沿两个励磁磁极方向上的作用力,即水平和竖直方向的作用力,可实现对两个方向上力的同时检测,更加符合实际工况,采用对称式结构一方面可以增大内部磁通量,另一方面减小了由于感应磁芯空间位置上的磁通量损耗。对该传感器的磁路结构进行公式推导,利用数学模型阐述了传感器的工作原理,并通过仿真和实验验证了理论的可行性,得到了在不同外界作用力下传感器的输出特性曲线,根据此曲线可以得到相应的灵敏度,验证了双十字轴对称式力传感器具有较高的灵敏度和较好的线性输出特性,更适合于现代农业机械设备。
