超声多普勒流量信号的多声道互相关检测方法∗
2021-12-15史风栋张宏伟苏焕鑫袁
史风栋张宏伟苏焕鑫袁 志
(1.天津工业大学控制科学与工程学院,天津300387;2.天津工业大学工程训练国家级实验教学示范中心,天津300387;3.天津可宏振星科技有限公司,天津300192)
超声多普勒流量计具有安装结构简单、非接触测量、不阻碍流体流动、不产生压力损失、适合多种管径使用等优点,在工业、农业等领域中快速发展。管道中的流体流动时,流体中的某些杂质对超声波产生散射作用,导致超声波的频率发生改变,而超声多普勒流量计正是根据这种频率的变化求得流体的流速和流量[1]。因此,在超声多普勒流量计的研究过程中,对超声波频率差信号的提取、对干扰噪声的滤除以及对滤波后的数据计算是超声多普勒流量计几个非常重要的部分[2]。前人所研究的超声多普勒流量计为了达到精确的测量结果,在硬件上先后采用了微处理器、DSP或者两种相结合的方式对采集信号进行处理[3-5],以及将FPGA技术也应用于此,来提升对信号处理的能力[6]。在软件算法上,对超声多普勒信号的噪声处理也做了大量的工作。比如文献[7]采用阈值抽取谱峰搜索的方法,通过对多普勒信号进行平方放大的方式修正多普勒信号,避免了寻找峰值过程中产生的随机性;在对不同的流体进行测量时,如果选取的阈值不合适,可能导致测量结果出现不确定偏差。文献[8]利用自相关函数处理超声多普勒信号中的噪声干扰,以降低超声多普勒流量计的测量下限;而计算过程中信号的长度越短,计算出的结果性能越差,测量的精确也随之下降。文献[9]使用小波阈值去噪的方法滤除干扰,但是存在一定的缺陷。比如硬阈值函数不连续,或者软阈值函数中的估计小波系数和噪声信号的小波系数之间有固定偏差等,也会降低测量的精度。文献[10]采用ZOOM-FFT选带细化频谱分析方法处理采集的超声波信号,但这种算法需要采集的数据量较大,并且细化后频谱局部有可能会失真,因此其应用也受到一定限制。
本文采用多声道对超声多普勒流量信号进行采集,并将多重互相关函数和FFT谱分析技术[11]相结合,对采集信号做滤波处理,该方法可以保留有效信号,较好地滤除噪声干扰[12],为低流速下流量信号的测量创造良好条件。
1 超声多普勒流量测量原理
超声多普勒流量计就是利用声波的多普勒效应设计出来的[13]。波源和观察者之间相对运动的过程中,观察者接收的频率和波源发出的频率之间存在差值,称这个现象为多普勒效应,二者的差值称为多普勒频移,且正比于相对运动速度。如图1所示为超声多普勒流量计的模型。根据超声波多普勒流量计模型简述其测量原理并推算出多普勒信号的频移与流速之间的数学关系。

图1 超声多普勒流量计模型
超声波发射器向管道中发射超声波且与水平之间的为夹角θ,当杂质以速度v沿着管道的中轴线运动时,相对超声波发射器,杂质是以速度v cosθ离去的,此时杂质充当“观察者”,对于发射器却是运动的;杂质接收到超声波后将其散射到接收器,接收器充当“观察者”,相对杂质是运动的[14]。故可求得多普勒频移f为:
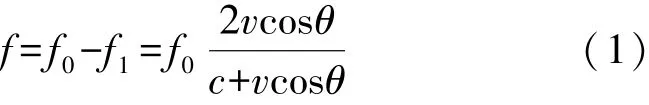
式中:f0为超声波发射频率;f1为超声波接收频率;c为超声波在介质中的传播速度。
已知超声波的速度远远大于流体流速,即c≫v cosθ,则根据公式(1)求得流体流速v为:

根据上述推导的公式可知,使用超声多普勒流量计进行流量测量时,在超声波发射频率以及超声波入射角已知地情况下,想要测量管道中流体的流速v,只需精确地得到多普勒频移f即可。然后根据测得流速和管道的口径即可以进一步求出管道中的液体的流量。
2 超声多普勒信号处理
2.1 互相关算法理论
互相关函数可以清晰地展示出在某时间段内随机信号之间的相关性。当不考虑噪声的情况下,输入信号和输出信号的波形是一样的,输出信号在时间上滞后。在平稳的随机过程中,采集信号会淹没在噪声中,通过互相关算法可以将信号之间的相关特性保留,滤除无相关特性的信号和噪声[15]。
假设理想平稳的随机信号序列x(t)和y(t)分别由有用信号X(t)、Y(t)和噪声信号nx(t)、ny(t)组成,如下式(3)所示:
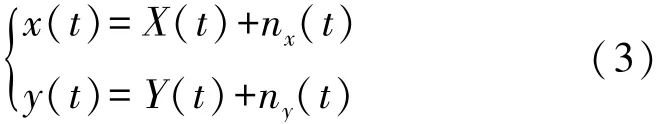
则两个信号做互相关运算定义为:

式中:τ为延迟时间,T为采样时间。将式(3)中的x(t)和y(t)分别代入式(4)中,得到有用信号和噪声信号之间的关系,如下式(5)所示:
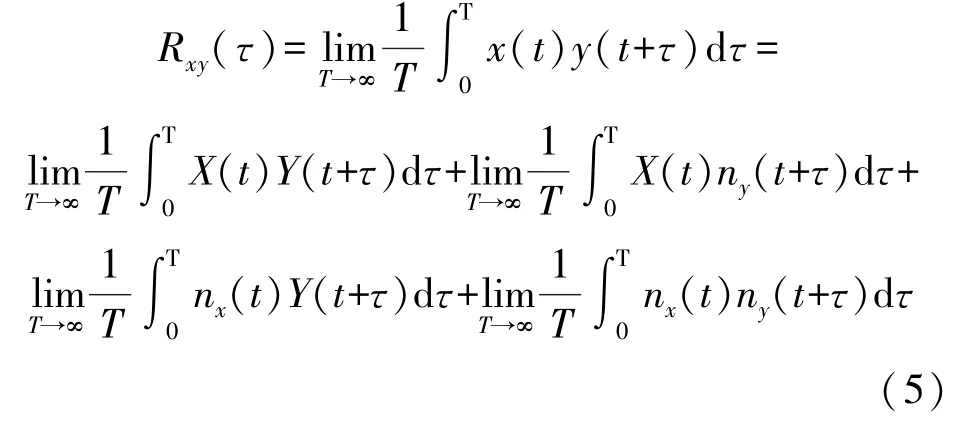
由互相关性质可得,有用信号与噪声信号之间不存在相关特性,并且噪声信号之间也不存在相关特性。故X(t)、Y(t)与nx(t)、ny(t)不相关,并且nx(t)、ny(t)之间也不相关,又因是理想情况下,采样时间T趋向于无穷大,则式(5)中第一项有相关性不为0,后三项没有相关性则都为0。x(t)和y(t)互相关的结果就是第一项,即滤除噪声后的结果如式(6)所示。
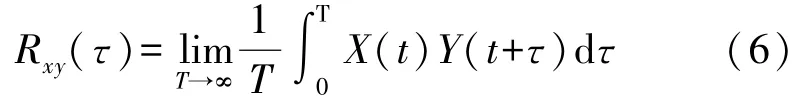
互相关运算是基于对两组数据序列的相关性分析,当这两组的数据序列差异较大时,互相关后的结果的准确性也较差[16]。因此在使用互相关运算时应该注意信号采样过程中尽量减小两个序列的差别。
2.2 多重互相关算法
由上述的分析可知,互相关在处理噪声干扰方面存在一定的优势。在实际测量的过程中,超声多普勒信号的采集会受到某些因素的干扰而携带大量噪声,若直接将其用于计算会对测量造成巨大误差,影响测量结果的准确性。而对于含有噪声干扰的采集信号仅做一次互相关运算而得到准确的多普勒信号是非常困难的,故提出对采集信号使用多重互相关算法进行处理[17],将其中的噪声干扰降到最低,改善信号信噪比。
假设y0(t)、y1(t)和y2(t)分别是多通道超声多普勒流量计采集的信号并且含有各种噪声干扰,如下式(7)所示:

式中:x0(t)、x′0(t)和x″0(t)是频率相同的有用信号,n0(t)、n1(t)和n2(t)分别为存在的噪声干扰信号。
首先,信号y0(t)和y1(t)进行互相关运算,得到信号y01(t),其计算过程如式(8)所示:

式中:x0(t)和n0(t)、n0(t)和n1(t)没有相关性,所以随着采样时间T趋向于无穷大时,其结果为0。然而,现实中采样时间T不可能为无穷大,故对式(8)中的第一项定义为x1(t)是y0(t)和y1(t)互相关的结果,后三项定义为噪声信号n01(t),并且n01(t)是不断趋向于0但不为0的并远远小于n0(t)和n1(t)的值。化简后结果如式(9)所示:
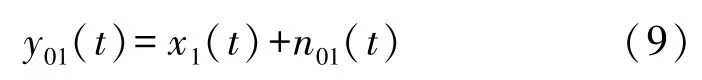
同理,信号y0(t)和y2(t)做的互相关运算,并同样将其化简得到信号y02(t),如下式(10)所示:
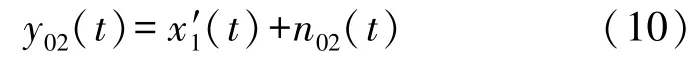
式中:x′1(t)是y0(t)和y2(t)互相关的结果,噪声信号n01(t)是不断趋向于0但不为0的并远远小于n0(t)和n2(t)的值。
通过上述的运算后得到两组新的超声多普勒信号序列y01(t)和y02(t)。这两组信号中的有用信号与原信号相同,即多普勒信号没有因为互相关计算发生变化,但其中所含有的部分噪声干扰在互相关的过程中被滤除。
为了进一步精确测量结果,将y01(t)和y02(t)作为新的两组数据并进行互相关计算,结果信号Z1(τ)如下式(11)所示:

借助互相关性质,将结果Z1(τ)化简得式(12)所示:

式中:X1(t)是信号y01(t)和y02(t)互相关的结果。N1(t)是噪声信号,是不断趋向于0但不为0,并远远小于n01(t)和n02(t)的值。
随着互相关算次数的增加,噪声信号的干扰就会越来越少,有用的多普勒信号会越来越明显,当与y02(t)做n次互相关并对其化简后可得到如式(13)所示的结果:

信号多次互相关运算后,信号Zn(t)中的有用信号Xn(t)的特点并未变化,即与原信号中x0(t)的频率相同。噪声信号Nn(t)的干扰对相对于原信号已经微乎其微,并远远小于原信号中的n0(t)、n1(t)和n2(t)。由此也说明信号Zn(t)的信噪比相对于原信号y0(t)、y1(t)和y2(t)更高。
2.3 算法仿真和验证
为验证其算法的可行性,测量管道中水流的流速为例。超声波的发射器和和接收器固定于管道的外侧,发射器发射频率为1 MHz的连续超声波信号经过声楔进入管道中,受到水中杂质或气泡散射后被接收器接收,对接收信号处理后得到含有噪声干扰的多普勒频移信号。如图2所示,首先将接收到的超声波信号与1 MHz的参考信号同时接入乘法器得到混频信号,混频信号中除了含有被反射后的超声波信号和1 MHz的参考信号外,还存在这两者的和频信号以及差频信号等,然后使用低通滤波的方式将混频信号中的差频信号保留,最后将差频信号进行放大处理,得到含有噪声干扰的多普勒频移信号。通过软件算法对多普勒频移信号进行数据处理,将噪声干扰滤除后的结果输出,对结果进一步分析。

图2 多普勒频移信号的获取
如图3所示为多声道超声波多普勒流量计在管道中水流速为0.2 m/s时,超声波发射频率为1 MHz的环境下得到的三组多普勒频移信号数据,定义其为x、y、z。从时域图中可以看出信号x、y、z是非常混乱的且没有规律的多普勒频移信号,噪声干扰影响了波形的平稳性,上下波动存在随机性。

图3 原信号时域图
将上述三组采集的信号经过FFT变换后得到如图4所示的频谱图。由于存在各种噪声的干扰,在其频谱图上出现不同频率的峰值,无法准确得到超声波多普勒频移信号的频率值,只是可以粗略地确定其频率范围。由此,想直接通过未处理信号的频谱得到多普勒频移是非常困难的。也进一步说明直接使用未经处理的多普勒频移信号计算流速将会造成较大误差,影响测量的精度。

图4 原信号的频谱图
根据上述的多重互相关算法,首先将信号x和信号y做互相关运算,信号x和信号z也做同样的运算,其结果如图5所示,可以看出虽然进行了互相关操作,但是得到的两组数据的时域波形依然是毫无规律的波形信号。由此也证明了仅使用一次互相关运算不能完全滤除噪声对超声多普勒信号的干扰。将图5中的时域信号经FFT变换至频域,得到图6所示的频谱图,其中也依然存在噪声信号对超声多普勒信号的干扰,但是相对原信号中的噪声干扰已经明显减少,并能够确定超声多普勒信号的频率范围大约在100 Hz到300 Hz之间。
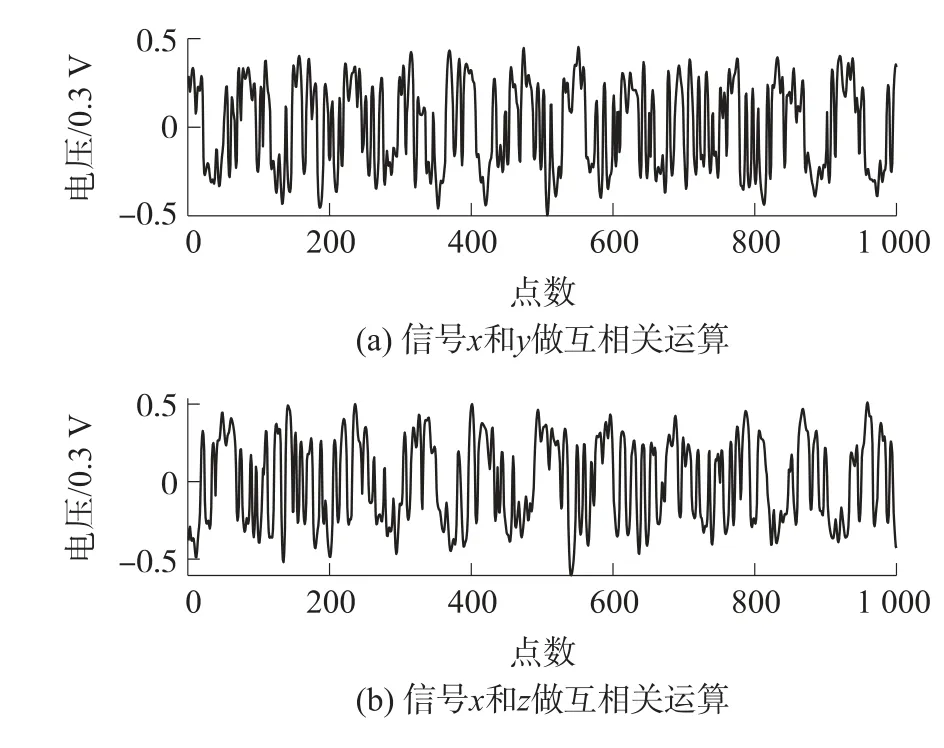
图5 两两互相关的时域图

图6 两两互相关的频谱图
为了得到稳定的超声多普勒信号,利用多重互相关的优势,将上述互相关后的两组数据作为进行多重互相关运算的原始数据,对其进行滤波优化。如图7所示,首先将两组数据进行第一次互相关运算,在其时域图7(a)中看出信号波形虽存在不同频率的噪声干扰,但是呈现出周期变化的趋势。图7(b)是第二次互相关运算后的结果,其中信号波形按照一定规律周期性波动,说明进行到第二次互相关运算后其中的噪声大部分被滤除,但是存留的部分干扰使信号波形在波峰和波谷的位置出现小范围的变化,导致波形并不平滑。图7(c)是当经过第三次互相关运算后,超声多普勒信号的噪声干扰几乎被滤除,多普勒信号呈现有规律的周期变化,并且信号的波形较为平滑。由图7(c)的结果可计算出多普勒频移为178 Hz,将其代入多普勒流速计算公式后求出管道中的流速为0.191 m/s。

图7 多重互相关运算时域图
对比多重互相关运算前后可知,不同频率的噪声信号几乎被滤除,有效地保留了多普勒频移信号的信号特征,并且经过多重互相关运算后的信号更利于得到较为精确的多普勒频移,信号的信噪比明显提升。由理论和仿真结果可知,虽然多重互相关的算法可以有效地降低噪声信号的占比,但随着多重互相关次数的增多,计算量也会增大,对硬件数据处理能力和处理时间带来考验;而如果多重互相关次数较少,其结果也不够精确,为后续的测量带来较大的误差。因此,应该根据实际测量环境、管道的口径以及测量中的一些参数确定多重互相关的次数。
3 实验验证
通过室内的液体流量试验平台,对所设计的多通道超声波流量计的测量精度进行实验验证。实验所用液体流量测量平台中管道的型号为DN150,管道中测量的液体是含有气泡、铁锈和泥沙等杂质的自来水。本实验选择一个超声波发射器和三个超声波接收器作为多通道超声多普勒流量计的发射装置和接收装置,安装位置如图8所示。采用STM32F103微处理器作为流量计的控制单元和运算单元,将接收到的信号进行硬件滤波和放大处理,并采用上述多重互相关运算滤除噪声干扰,得到具有高信噪比的多普勒频移信号,进一步求得较为精确的多普勒频移量后代入流速计算公式完成对管道中的流速测量,并由管道的直径和流速计算出流量。

图8 超声波发射器和接收器的安装示意图
为检测其测量是否精确,采用0.5级的电磁流量计作为标准表,对比多通道超声多普勒流量计的测量结果。调节液体流量试验平台中变频器的频率,控制管道中水流的流速在0.2 m/s~2.5 m/s之间。统计标准表和超声多普勒流量计的流速测量结果,并根据实际流速和测量流速计算出相对误差,如表1所示。

表1 试验结果
根据在液体流量测量平台上所做实验的分析可知,当水流速较低时,水流中的铁锈、泥沙等杂质量以及水中的气泡量较少,随着流速的增大,水流中含有的铁锈、泥沙等杂质量和气泡量逐渐增多,超声波被散射的能力也增强,故在增大水流速的过程中其相对误差也逐渐减小。由表1的实验结果说明了在低流速环境下,使用多通道超声多普勒流量计的测量效果良好,并且对比标准表之间的相对误差较小,测量精度满足要求,较好地实现了对管道中流速的检测。
4 结论
本文将多重互相关算法应用于多声道超声多普勒流量计中,使用多重互相关滤除信号中的噪声干扰,减小噪声信号在测量中误差,提升了信号的信噪比。对仿真结果的分析,表明通过FFT谱分析和多重互相关算法可以将超声多普勒信号中无关的噪声干扰滤除。同时在室内的液体流量试验平台上进行实验,也得到了较为精确的流速测量结果。在多重互相关运算的基础上结合FFT频谱分析,对多普勒信号处理的能力大大提高,进一步改善了超声多普勒流量计的测量性能。
