铺丝成形复合材料格栅筋条的纤维形态与弯曲性能评价

2021-12-15周来水安鲁陵

中国机械工程 2021年23期

赵聪肖军周来水安鲁陵

1南京航空航天大学机电学院，南京，2100162南京航空航天大学材料科学与技术学院，南京，210016

0 引言

先进复合材料格栅结构作为复合材料先进结构形式之一，具有优异的结构稳定性、抗损伤能力、高损伤容限以及出色的结构减重效益，在航空航天飞行器级间段、承力筒中应用广泛[1-3]。随着先进复合材料应用领域不断拓宽、航空航天器起飞质量不断增大、续航距离不断提高，传统复合材料格栅结构已然无法满足越发严苛的性能要求和轻量化要求。进一步减轻结构件质量，提高结构件的承力性能，研发具有更高承载效率的新一代复合材料格栅结构具有重要理论和工程应用意义。

目前，关于曲线化格栅结构的研究多集中于多种载荷作用下宏观结构的承载性能预测及非线性行为方面[4-6]，继而从理论角度建立起曲线化格栅结构宏观结构参数(格栅取向、格栅密度、格栅高度及格栅厚度)和最终结构性能的关联[7-10]。受曲线化格栅几何特点的约束，结构中通常存在纤维屈曲缺陷。与传统直线型格栅结构类似，相交的曲线化网格筋同样会在交叉节点处产生材料堆积，引起厚度的变化，导致纤维面外屈曲的产生[11-13]。现有研究表明，纤维屈曲的存在会导致复合材料性能显著下降，且对压缩性能的影响更为显著[14-18]。这也是格栅结构在压缩/压剪载荷工况作用下，起始损伤和最终失效位置往往集中于格栅交叉节点区域的原因[19]。然而，现有通过组合模具工艺结合纤维缠绕成形工艺，进而实现传统直线型复合材料格栅结构的成形工艺[20-22]，无法避免格栅节点处纤维的堆积。

近年来，快速发展的自动铺丝成形工艺(automated fibre placement，AFP)可实现对铺放材料的夹持、剪断和重送，理论上可以避免格栅节点处材料的堆积、减小纤维屈曲程度。加拿大ICCI公司和荷兰宇航中心已率先开展了自动铺丝成形技术对复合材料格栅结构的成形适应性研究，结果发现自动铺丝成形工艺在格栅节点尺寸控制以及筋条-蒙皮结合质量等方面体现出了其他成形工艺无法比拟的优越性[23-25]。

本文基于自动铺丝成形工艺特点，提出复材格栅筋条节点处纤维形态改善方法，验证“剪断-续铺”法引入的非连续铺层对节点纤维形态改善的可行性。在此基础上，结合复合材料格栅结构常见的服役条件，从简化试验流程的角度出发，选取弯曲承载性能，通过试验和仿真手段研究非连续铺层对格栅筋条弯曲载荷作用下失效行为的影响，确定格栅结构最优非连续铺层的含量和分布。

1 复合材料格栅筋条自动铺丝成形

1.1 原理

如图1所示，在自动铺丝成形过程中可以对铺放材料进行夹持—剪断—续铺操作。这意味着在进行格栅筋条铺放过程中，可以在节点前将预浸丝束剪断而在节点后对预浸丝束进行重送，避免节点处预浸丝束的重叠，减小纤维面外屈曲尺度，提高筋条力学性能；另一方面，夹持—剪断—续铺引入的非连续层，必然引起结构力学性能下降。

(a) 无剪断—夹持—续铺操作

1.2 试样制备

选用恒神股份有限公司提供的EM118/A10型预浸料为原料，纤维体积分数为63%，单层名义厚度为0.15 mm。以南京航空航天大学自行研制的格栅铺丝机为试验平台，制备含不同非连续铺层比例和分布方式的复合材料格栅筋条，如图2所示。为了保证筋条上下层之间良好的铺放粘接质量，基于前期铺放工艺参数优化试验结果，本文在进行不同类型格栅筋条铺放过程中采用相同的铺放工艺参数：铺放压实力500 N、铺放速率200 mm/min、预浸料表面加热温度30 ℃。

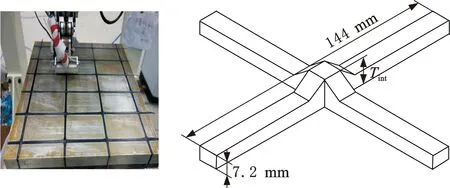
(a) 自动铺丝试验平台 (b) 格栅筋条尺寸示意图图2 复合材料格栅筋条自动铺丝成形Fig.2 Manufacture of grid stiffeners via AFP

为了研究非连续层含量和分布对格栅节点处纤维屈曲尺度的影响，设计了8种不同类型格栅筋条并采用如下命名方式：AGS-R-U/T/C/B。其中AGS(advanced grid stiffener)代表先进格栅筋条；R为筋条节点处非连续层的含量；U、T、C、B分别代表非连续铺层在格栅节点厚度方向的分布方式，U为均匀分布，T代表顶部区域集中分布，C代表中部区域集中分布，B代表底部区域集中分布。AGS-25-T代表非连续层在节点处铺层的含量为25%且非连续铺层集中分布于顶部区域内的格栅筋条。不同类型格栅筋条节点厚度与横截面形态见图3。从图3中可以看出，格栅筋条节点厚度Tint受非连续铺层含量影响显著，而集中式分布的非连续铺层则会显著改变格栅节点处纤维的细观形态。

(a) 屈曲表征 (b) AGS-Baseline (c) AGS-12.5-U

2 非连续铺层对格栅节点纤维形态的影响

2.1 格栅节点纤维形态表征与描述

为了简化模型，通常将图3a所示的波浪起伏式分布的面内屈曲纤维近似为振幅为A、波长为L的正弦函数曲线[26-28]。纤维屈曲尺度可以利用最大振幅波长比λ=A/L和最大纤维偏转角θ描述，振幅波长比越大，最大纤维偏转角也就越大，纤维面外屈曲尺度也就越大。

2.2 非连续铺层含量的影响

利用Leica DVM5000型光学显微镜对含不同非连续铺层含量的格栅节点纤维形态进行显微观察，结果如图3b～图3f所示。随着格栅节点处引入的非连续铺层增加，节点处材料堆积程度越小，纤维屈曲尺度也就越小。进一步测量各筋条节点处面外屈曲纤维的最大振幅波长比λ、最大纤维偏转角θ和振幅或节点-筋条厚度差A，结果如表1所示。

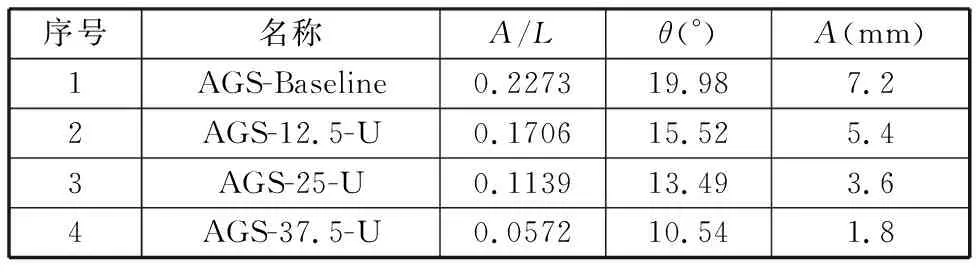
表1 非连续铺层对节点纤维屈曲尺度的影响

显然，节点纤维屈曲尺度与节点-筋条厚度差A显著相关。随着格栅节点处非连续铺层含量的增加，节点-筋条厚度差迅速减小。非连续铺层含量达到50%时，节点-筋条厚度差为零，纤维屈曲也被消除。格栅筋条-节点厚度差与纤维面外屈曲的最大振幅波长比之间的关系拟合式为

λ=0.0312A+0.0002

(1)

后续可以利用该公式对其他类型格栅节点处纤维面外屈曲尺度进行预测。

2.3 非连续铺层分布的影响

对比含相同含量、不同分布方式非连续铺层的格栅节点截面显微图(图3d、图3h～图3j)发现，格栅筋条中非连续铺层含量一定，则节点最大纤维屈曲尺度不变,但非连续铺层分布变化会引起节点处微观叠层结构的差异，必将引起格栅筋条在载荷作用下的力学行为。因此，需进行实际性能测试，深入研究非连续铺层对格栅力学行为的影响规律。

3 非连续铺层对格栅筋条抗弯性能的影响

3.1 非连续铺层含量的影响

参照GB/T 3356—2014，利用SANS CMT-5504型万能试验机对上述不同类型格栅筋条进行三点弯曲测试。其中，加载头半径5 mm，支座半径3 mm，支座跨距80 mm。所得载荷位移曲线见图4a。从图中可以发现，格栅筋条在弯曲失效过程中并没有呈现复合材料的脆性突然失效行为，而是呈现了与金属等韧性材料类似的伪韧性断裂行为。伪韧性行为可以利用伪韧性位移进行表征，即载荷位移曲线中极限载荷对应位移到载荷下降率大于50%(判定试验结束)的对应位移差，如图4b所示。伪韧性位移越大，伪韧性行为越明显。

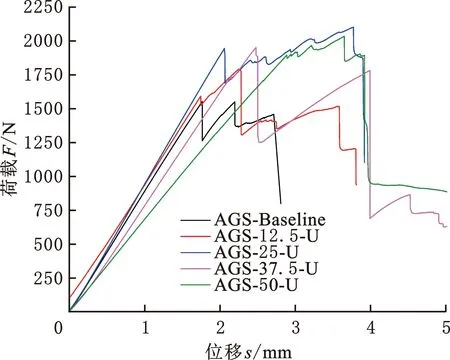
(a) 含不同非连续铺层含量的筋条弯曲载荷位移曲线

综上所述，为全面研究非连续铺层引入对格栅失效行为的影响，定义承载能力保持率RS和伪韧性位移占比RP。其中，承载能力保持率RS为剩余弯曲载荷FR和极限弯曲载荷FM的比值，而伪韧性位移占比则为极限弯曲载荷至完全失效过程中经历的伪韧性阶段位移DP与完全失效位移DF之间的比值。承载能力保持率越大、伪韧性位移占比越高，伪韧性行为越明显。

随着非连续铺层含量的不断增加，筋条-节点厚度差逐渐减小，节点处纤维形态不断改善，格栅筋条承载性能不断提高；然而随着非连续铺层含量的进一步增加，格栅筋条承力路径中断程度也不断增加，性能开始下降。当这两种影响达到平衡时，格栅筋条的弯曲性能达到最大值。两种影响的共同作用使格栅筋条极限弯曲载荷随非连续铺层含量的增加而先上升后下降，如图5a所示。此外，非连续铺层含量还对格栅筋条弯曲载荷作用下的伪韧性行为产生影响，如图5b所示，在非连续铺层在格栅节点厚度方向上均匀分布的前提下，当非连续铺层含量达到50%时，格栅筋条的承载能力保持率达到最大，而格栅筋条弯曲载荷作用下伪韧性行为则在非连续铺层含量为25%时最为显著。

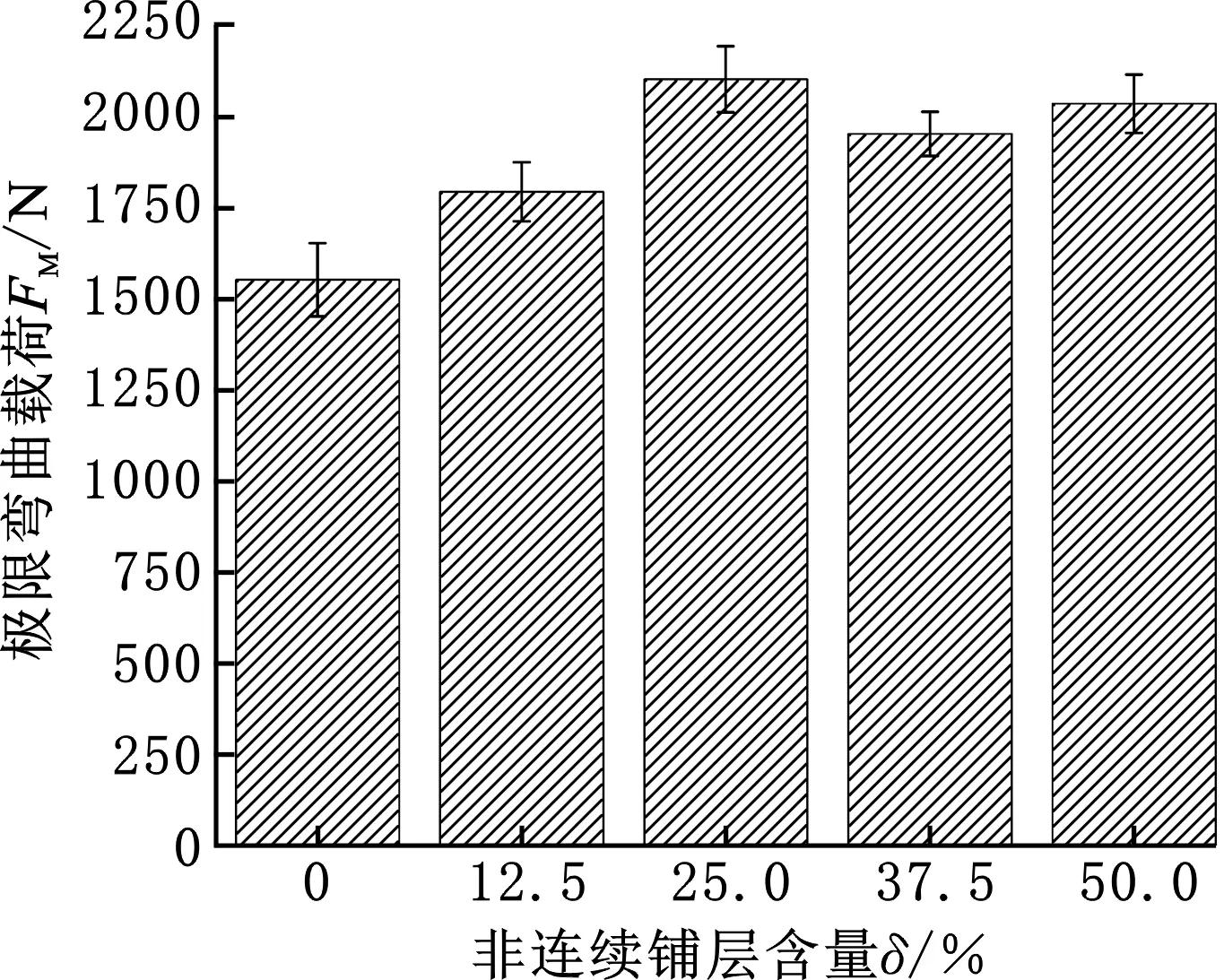
(a) 对筋条极限弯曲载荷的影响

综合非连续铺层含量对筋条弯曲极限载荷、承载能力保持率和伪韧性行为显著性的影响，当非连续铺层在筋条厚度方向均匀分布时，非连续铺层含量为25%时最优。

3.2 非连续铺层分布的影响

在确定了最优非连续铺层含量的情况下，通过试验的方法进一步研究非连续铺层分布方式对格栅筋条抗弯能力的影响，结果如图6所示。

(a) 对筋条极限弯曲载荷的影响

非连续铺层分布方式显著影响格栅筋条的弯曲承载能力。当非连续铺层呈底部集中分布(AGS-25-B)时，虽然实现了极限承载能力最大化，但其伪韧性行为可以忽略，呈现脆性行为；当非连续铺呈顶部集中分布(AGS-25-T)时，格栅筋条既可以获得相当的极限承载能力，也可以获得最为显著的韧性行为，这种高韧性往往是复合材料结构特别是主承力结构所追求的特性，可防止整个结构突然失效，避免重大损失。

4 含非连续铺层格栅筋条弯曲失效行为

4.1 有限元仿真模型的建立

以ABAQUS 2020为平台，采用“ply to ply”建模方法，结合实际筋条几何尺寸和测试条件，建立包含纤维屈曲和非连续铺层的三维格栅筋条有限元仿真模型(图7)。模型中，支撑端和加载压头视为刚体，支撑端施加固定约束，而加载压头施加10mm的下降位移。支撑端、加载压头与试样接触面定义为硬接触，摩擦因数为0.3。铺层单元类型为SC8R连续壳单元。铺层间插入0厚度、网格类型为COH3D8的cohesive单元以表征试样内部分层起始与演化。

(a) 网格划分

采用Hashin失效准则[29]对复合材料的失效行为进行预测。该失效准则中，复合材料的失效模式包含纤维拉伸失效、纤维压缩失效、树脂拉伸失效和树脂压缩失效，各失效模式对应的失效应力计算公式如下：

纤维拉伸失效应力

(2)

纤维压缩失效应力

(3)

基体拉伸失效应力

(4)

基体压缩失效应力

(5)

式中，XT、XC分别为平行于纤维排布方向上的最终失效拉伸和压缩应力；YT、YC分别为垂直于纤维排布方向上的最终失效拉伸和压缩应力；SL、ST分别为纤维纵向和横向的剪切失效应力；α为剪切应力对纤维拉伸行为的影响因子，此处取α=1[30-31]；σ11、σ22、τ12为各个方向上的应力分量。

满足上述任何一个失效条件，则判定材料失效。

选用层间拉伸分离定律和混合失效模式对层间失效的起始和扩展进行分析。拉伸分离后材料呈现双线性特性直至拉伸刚度退化至0，分层损伤起始可以根据混合模式下的二次应力准则进行判断：

(6)

整个单元的失效则可以利用能量准则进行表征：

(7)

式中，Gn、Gs、Gt分别为所用材料的Ⅰ型、Ⅱ型和Ⅲ型断裂能；GⅠC、GⅡC、GⅢC分别为对应断裂模式下的断裂韧性/临界断裂能。

一旦层间应力满足式(6)，则层间内聚单元性能开始退化直至自动删除。相关材料性能参数和层间性能参数详见表2。

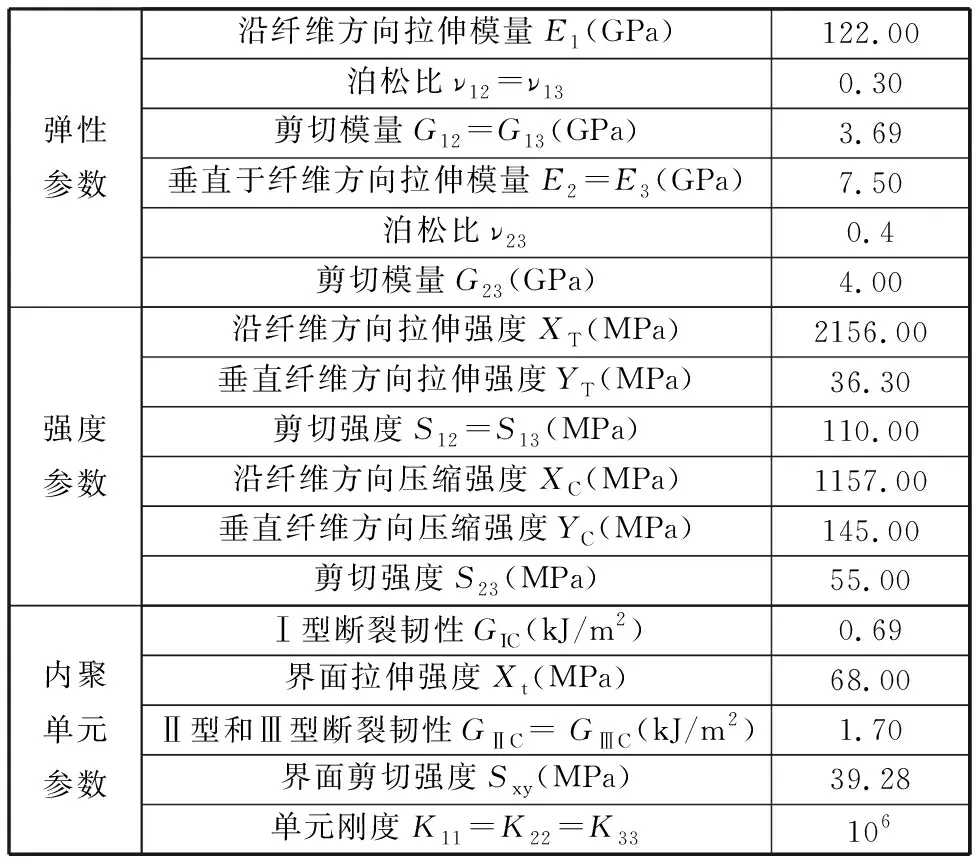
表2 EM118/A10型预浸料力学性能参数

4.2 非连续铺层含量对格栅筋条弯曲失效行为的影响

仿真和试验所得筋条弯曲载荷位移曲线与极限弯曲载荷的对比如图8所示。为了提高建模速度和后期计算效率，在进行有限元建模时，将格栅筋条-节点过渡区内实际呈曲线状态的纤维进行了直线化处理，同时忽略了横向铺层和纵向铺层间的微小富树脂区。上述原因造成了仿真结果和试验结果之间的偏差，如图8a所示。经过深入对比可知(图8b)，对不同类型的格栅筋条来说，仿真所得极限弯曲载荷与试验结果偏差均小于8%，证明了仿真模型的可靠性，相关筋条弯曲载荷作用下的失效行为可以采用该有限元模型进行分析。

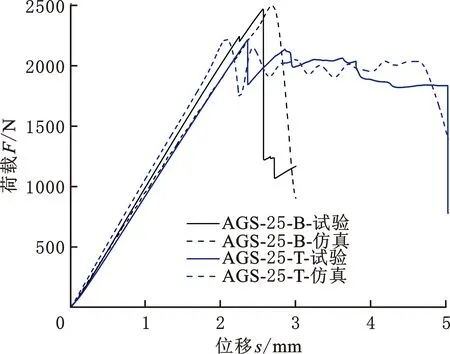
(a) 载荷位移曲线对比

利用所建立的仿真模型，对含不同非连续铺层含量筋条弯曲载荷作用下的力学行为进行研究，结果见图9。对于不含非连续铺层的筋条(图9a)，在弯曲载荷作用下，筋条底部纤维率先在拉应力作用下发生拉伸失效；随着载荷的逐渐增加，节点处连续铺层间发生分层损伤并发生横向扩展；与此同时，上表面铺层压缩应力显著增加，且纤维屈曲尺度越大，压缩应力越大，引起格栅结构的压缩失效；铺层偏转角度越大，层间剪切应力也就越大，使得在较低载荷水平便会引起分层，极大程度上降低了格栅筋条的极限承载能力。因此，在格栅筋条的设计和制造过程中，应尽可能地减小格栅筋条节点处纤维屈曲偏转角或铺层偏转角，以保证最终结构良好的性能。

(a) AGS-Baseline

当格栅筋条节点处非连续铺层占比达到25%时，筋条表现出更为显著的弯曲韧性行为，格栅筋条可以维持其极限载荷85%的承载能力，且伪韧性位移占整个失效位移的53%(图9b)。弯曲载荷作用下，格栅筋条顶部区域受压，底部区域受拉。随着弯曲载荷不断地增加，顶部区域内压缩应力显著增加，引起了顶部区域内分层失效和树脂压缩失效，导致载荷-位移曲线陡然下降；而分层后的非连续纤维在弯曲载荷的作用下产生滑移，并将弯曲载荷向下传递，载荷可以由尚未失效的区域继续承担；与此同时，分层沿格栅长度方向上不断扩展，非连续铺层继续滑移，维持一定的承载能力，从而表现出了韧性行为；当承载区域内部应力超过失效应力时，承载区域内纤维或树脂失效、裂纹迅速扩展，导致承载区域部分或全部突然失效，表现为载荷位移曲线的陡降。其他含均匀分布的非连续铺层格栅筋条也呈现了类似的失效行为。

非连续铺层的引入不仅可以改善格栅筋条节点处纤维形态，提高格栅筋条的极限承载能力，同时，利用非连续铺层和连续铺层间的滑移[32]，也能够实现格栅筋条失效行为的改善，完成具有韧性失效行为的复合材料格栅筋条的制造。

4.3 非连续铺层分布对格栅筋条弯曲失效行为的影响

如前所述，非连续铺层分布虽然对格栅筋条内部最大的纤维屈曲尺度无影响，但会在其内部引入不同的微观叠层结构，从而影响格栅筋条的失效行为。同理，对比分析非连续铺层分布方式不同时筋条的失效行为，结果如图10所示。

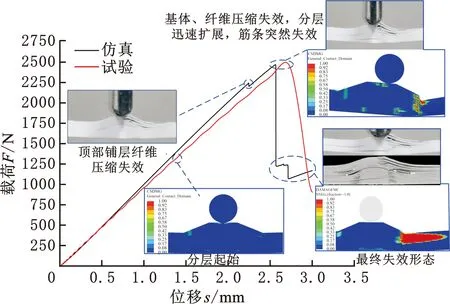
(a) AGS-25-B

对于非连续铺层底部集中分布的筋条(AGS-25-B，图10a)，载荷增大，导致顶部区域在压应力作用下产生分层和纤维压缩失效，筋条承载能力下降，体现在载荷位移曲线上为斜率的变化。载荷继续增大，底部区域集中的非连续铺层和连续铺层在压应力作用下发生滑移，从而导致大量分层产生，失效区域不断向格栅筋条厚度方向的中间区域扩展。当拉伸应力大于纤维拉伸失效的临界应力时，内部产生贯穿性裂纹，导致试样的突然失效，并没有表现出韧性行为。

对于非连续铺层呈顶部区域集中分布的筋条(AGS-25-T)，因非连续铺层的存在，顶部区域内连续铺层的纤维屈曲尺度为定值，而其他区域内连续铺层中的纤维屈曲尺度则随着铺层高度的增大而显著增加。在这种情况下，分层将在上述两个区域间迅速产生，从而将格栅筋条分割为两个子区域。其中顶部子区域由非连续铺层、连续铺层和横向铺层组成，而底部子区域则可以视为无非连续铺层的格栅筋条。

随着弯曲载荷的不断增大，顶部子区域不断被拉直，在此过程中，非连续铺层与连续铺层间的滑移推迟了区域内纤维和基体的失效。与此同时，底部子区域在拉伸和压缩应力的作用下不断失效，导致承载能力下降，形成了载荷位移曲线上的陡降。其他区域继续承载、失效，且顶部区域内非连续纤维和连续铺层的滑移在格栅筋条中引入了伪韧性性行为，如图10b所示。

上述结果表明，格栅筋条铺丝成形过程中，利用铺丝成形工艺特点，合理地引入非连续铺层可以改善节点处纤维形态，从而实现极限弯曲承载能力的提高。在此基础上，通过合理的非连续铺层分布设计，可以在格栅筋条中引入韧性行为。上述结果验证了铺丝成形在复材格栅筋条制造上的先进性。