温度效应下的冻结砂土经验蠕变模型分析
2021-12-15马祖飞高亚飞
杨 明,马祖飞,高亚飞,张 雯
(1.陕西省一八五煤田地质有限公司,陕西 榆林 719000;2.安徽理工大学土木建筑学院,安徽 淮南 232001)
0 引 言
随着我国隧道、深基坑等地下工程的不断发展,在地下工程建设过程中通常利用人工冻结法建立临时冻结壁,而温度是影响冻结壁强度与稳定性的主要因素,因此需要探究在低温条件下周围土体的强度特性、蠕变变形规律等物理力学行为[1- 4],以此建立合适的本构模型并对其进行预测,以保证工程土体在开挖过程中的稳定性和安全性。
近年来,许多学者针对冻土进行了大量的试验探究,通过建立相应的本构模型来描述其力学性质,并取得了一定的的研究成果。赵晓东等[5]进行不同温度梯度的三轴蠕变试验,探究了温度对蠕变变形规律的影响。郭梦圆等[6]利用粒子群算法对S-M模型进行参数识别,将模型计算曲线与试验曲线进行对比,曲线吻合度较好,为预测土体蠕变变形提供了一种新的思路。罗飞等[7]为研究冻结砂土的蠕变特性,在元件模型的基础上,引入损伤变量,建立新的蠕变模型,较好地描述蠕变的全过程,尤其是加速度蠕变阶段。陈军浩等[8]考虑传统整数阶模型的不足,在广义开尔文中引入分数阶理论,模拟出人工冻土的稳态蠕变变形规律。刘萌心等[9]通过不同温度下进行的加载试验,并在一维蠕变模型中考虑应力历史的作用,采用回归分析的方式确定模型参数,与试验结果进行对比发现具有较高的精度。马冬冬等[10]对冻结砂土进行主动围压试验,并结合应力-应变曲线各个阶段变化特点,分析砂土破坏特征形态。杜海民等[11]通过分析三轴压缩试验数据,探究含水量对屈服面的影响,建立考虑含水量影响的偏应力-剪应变增量型函数关系式,通过该函数关系计算的模拟值与试验结果吻合度较高。
本文主要在冻结砂土单轴抗压强度试验基础上,对其进行不同温度以及加载应力下的单轴压缩蠕变试验,并进行影响因素分析。引入S-M经验蠕变模型,考虑温度和加载应力的影响,对模型参数进行识别,得到改进的冻结砂土S-M经验蠕变模型,为人工冻结法更好地应用于实际工程提供一种理论支撑。
1 单轴压缩蠕变试验
1.1 试验方案
本文采用西北地区的砂土作为研究对象,将含水率为16%的重塑砂土制作成尺寸为直径50 mm、高100 mm的圆柱试样,分别在-5、-10、-15、-20 ℃这4种温度水平下,采用分级加载的方式进行单轴压缩蠕变试验。基于冻结砂土单轴抗压强度试验,每个温度下试验的单轴抗压强度峰值为σ,分级加载应力分别为0.1σ、0.2σ,具体加载应力强度见表1。从表1可知,单轴抗压强度峰值随温度的降低不断增大。试验仪器采用WDT-100型冻土压力试验机,当试验满足试验力下降20.0%、应变超过8.0%、试验时间超过10 h这3种情形之一时,试验自动停止。
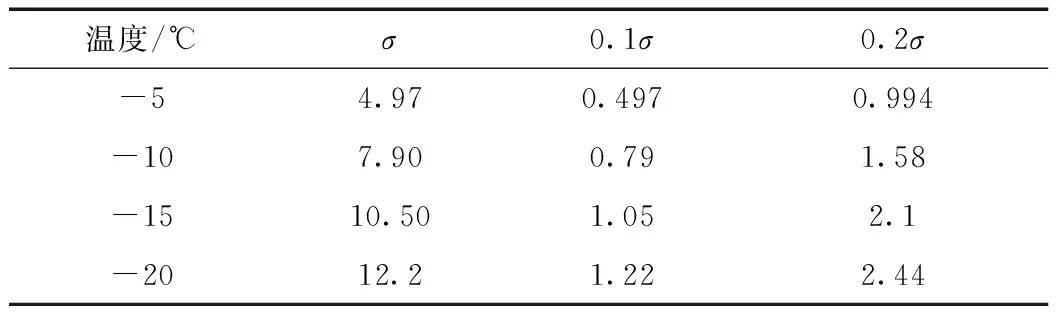
表1 冻结砂土加载应力强度σ
1.2 试验结果分析
冻结砂土单轴抗压强度峰值与温度拟合关系见图1。从图1可知,温度T与加载应力强度σ之间近似呈线性变化,函数表达式为
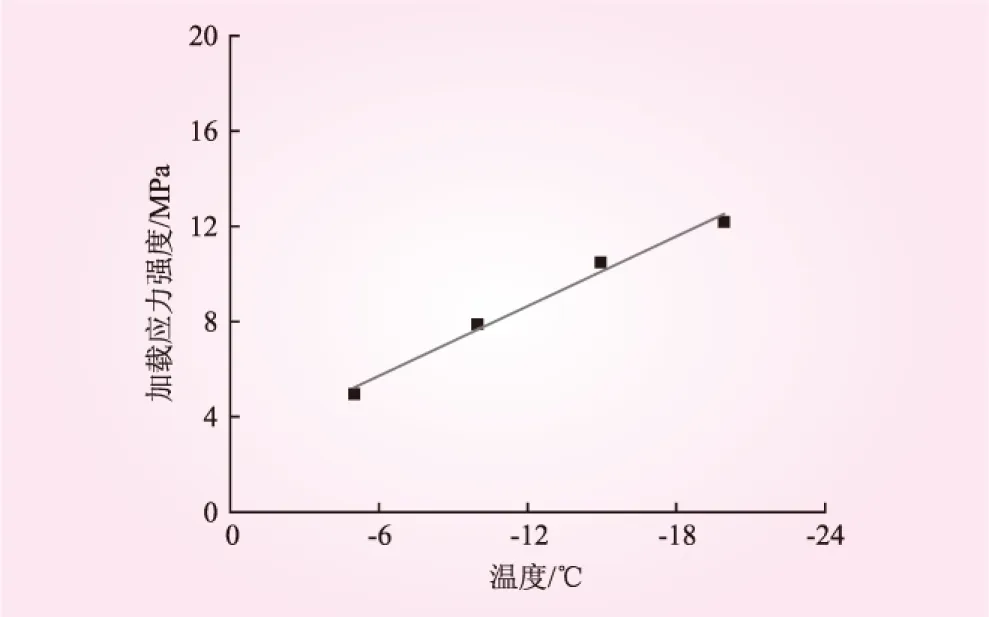
图1 温度与加载应力强度关系
(1)
不同温度及加载应力下的冻结砂土单轴蠕变试验曲线见图2。从图2可知,当加载荷载为低应力0.1σ和0.2σ时,试验曲线均表现为衰减蠕变阶段和稳定蠕变阶段,未呈现出加速度蠕变趋势。温度对蠕变变形量影响较大,在0.2σ加载等级下时较为明显。随着温度逐渐越低,试样中的未冻水逐渐减少,抗压强度增大,导致蠕变变形量逐渐减小。同一温度下,随着加载应力的增加,蠕变变形量也相应增加。不同温度及加载应力下的蠕变曲线均在较短时间内达到稳定状态。
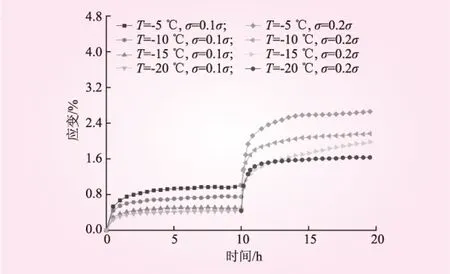
图2 不同温度及加载应力下的应变与时间的关系
2 冻结砂土经验蠕变模型
2.1 S-M模型
Singh等[12]总结提出了关于软黏土的S-M经验模型,以此预测土的蠕变变形特性。该模型还未应用于冻结砂土的蠕变变形中,本文尝试将其用于描述冻结砂土的单轴蠕变特性,其方程式如下
(2)

应力σ。对式(2)进行积分,不考虑初始应变,得
(3)
式中,ε为应变;σ为加载应力,令C=At1/(1-m)、B=1-m,得出S-M经验蠕变模型
(4)
2.2 模型参数识别
对不同温度下的蠕变试验曲线,取单位时间t1=1 h,对式(4)两边同时取对数,得
lnε=lnC+ασ+Blnt
(5)
图3为不同温度下lnε-lnt关系曲线。从图3可知,曲线近似呈线性关系,且同一温度下各加载应力作用下的拟合曲线斜率接近平行。经过拟合,得出不同温度以及加载应力作用下直线的平均斜率B,见表2。从表2可知,温度对斜率值B影响不大。因此,对不同温度下的斜率再取平均值,得出最终斜率为0.197 6。
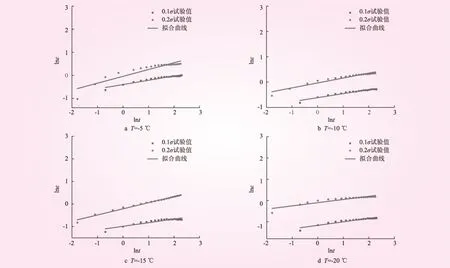
图3 不同温度下lnε-lnt关系

表2 不同温度下的斜率值B
取t=t1=1 h时作为参考时间,对式(4)两边同时取对数,得
lnε=lnC+ασ
(6)
表3为不同温度下的lnε的试验结果,当温度为-5 ℃时,将表1和表3中各加载应力和对数应变数据代入式(6),得

表3 不同温度下的lnε值
-0.448 8=lnC+0.497α
(7)
0.164 7=lnC+0.994α
(8)
联立式(7)、(8),求解出C和α值。同理,可求得其他温度下对应的参数C和α值,得出不同温度下的参数值,见表4。
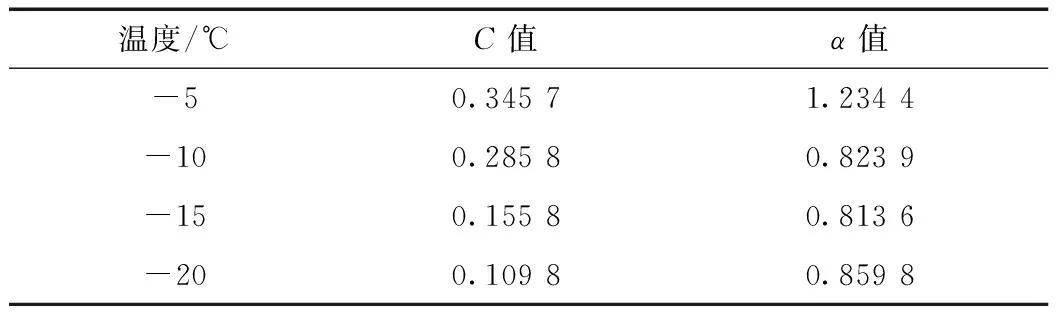
表4 不同温度下的C和 α值
通过拟合发现温度T和参数C值之间呈线性关系,见图4,函数关系式为
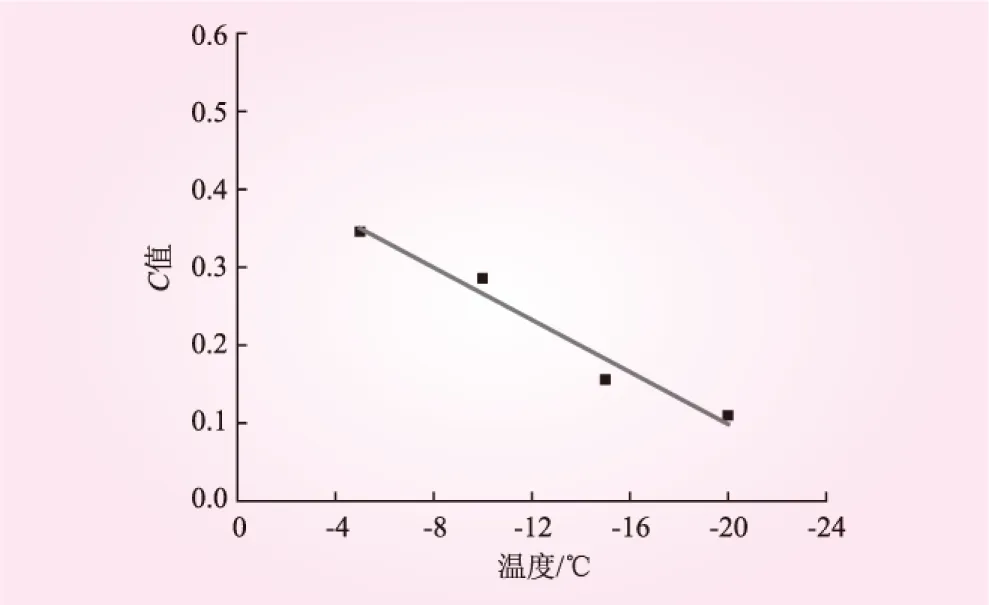
图4 温度T和C之间的关系
C=0.016 8T+0.433 7 (R2=0.966 0)
(9)
根据表4拟合发现,温度T和α值之间呈二次函数关系,见图5,函数关系式为
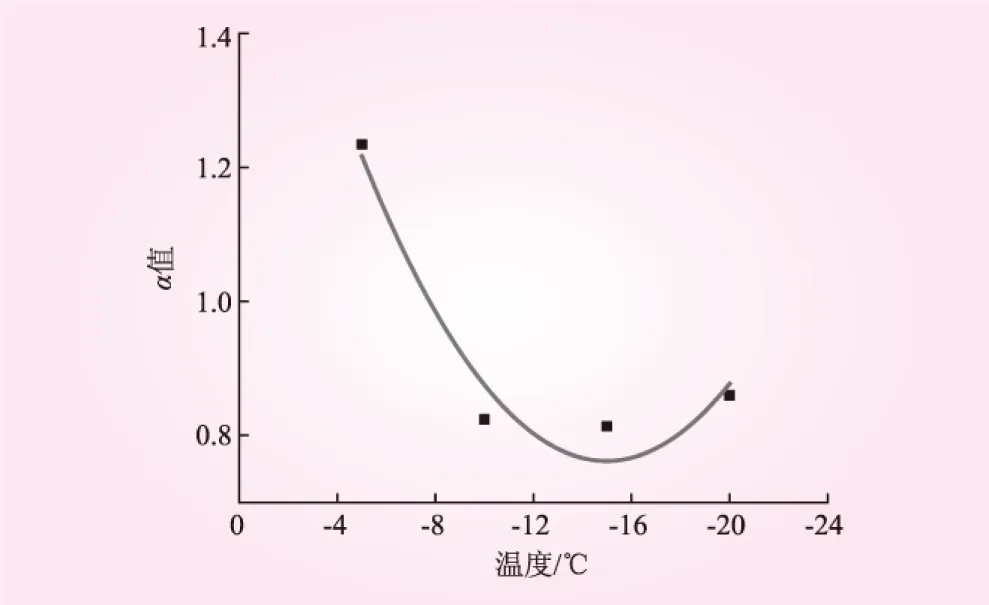
图5 温度T和α之间的关系
α=0.004 6T2+0.136 9T+1.787 3 (R2=0.951 7)
(10)
由此得出,考虑温度和加载应力为自变量的改进冻结砂土S-M经验蠕变模型
ε=C·eασ·t0.196 7
(11)
根据式(11)建立的改进冻结砂土S-M经验蠕变模型,计算出不同温度和加载应力作用下的冻结砂土的蠕变变形值,将计算结果与试验结果绘制出相应的曲线进行对比(见图6)。通过对比发现,该经验模型能较好地预测试验曲线整体趋势,表明该经验蠕变模型在冻结砂土应用方面具有一定的实用性。
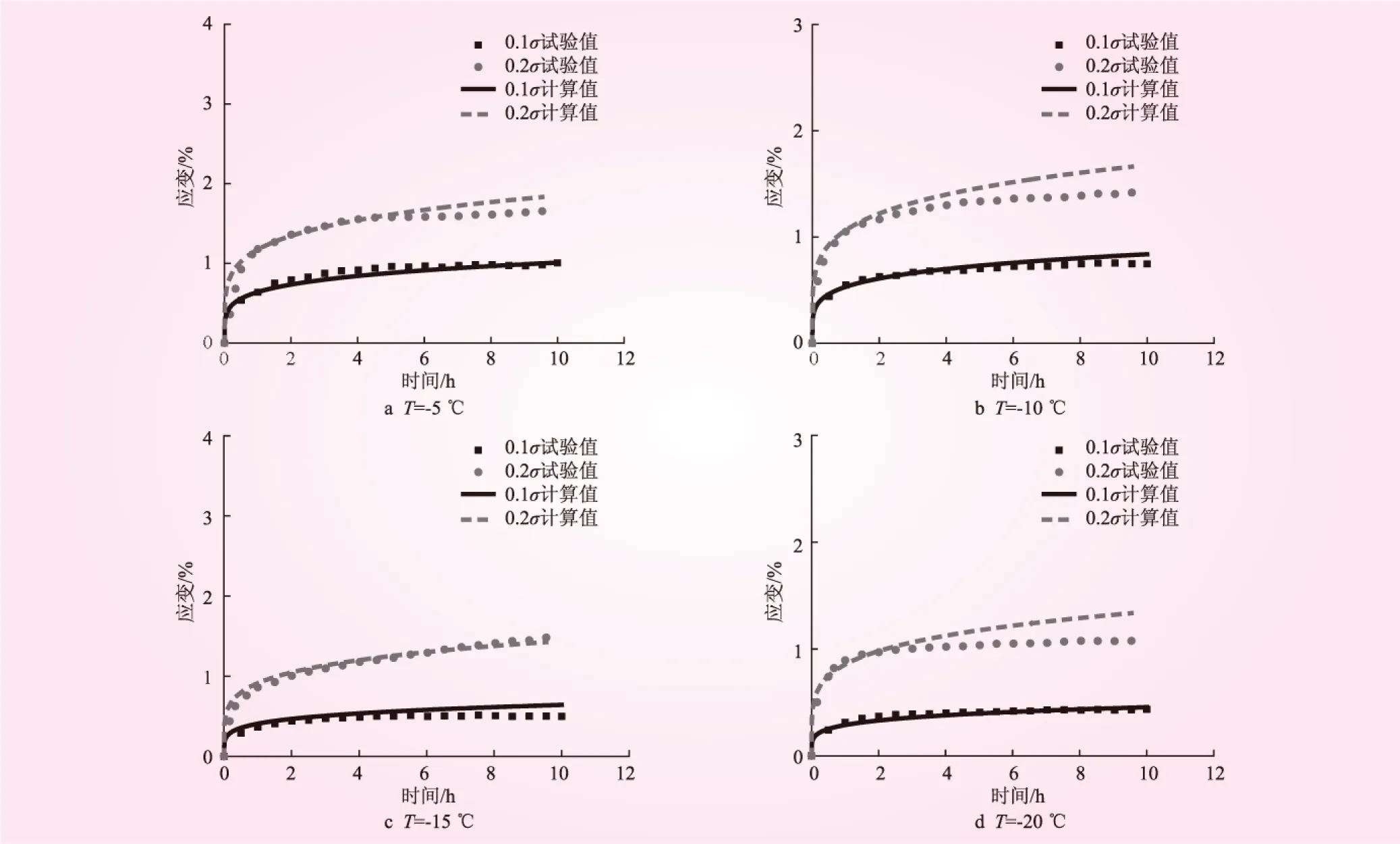
图6 不同温度下应变-时间关系对比
3 结 语
本文以西北地区的砂土作为研究对象,通过冻结砂土单轴压缩蠕变试验,建立温度和加载应力影响下改进的冻结砂土S-M经验蠕变模型,得出以下结论:
(1)在低应力不同温度作用下,蠕变曲线表现为衰减型蠕变,曲线过程中并未涉及加速度蠕变阶段,且温度越高,加载应力越大,砂土蠕变变形量越大。
(2)模型参数通过考虑温度的影响并利用计算的方式进行识别,相对于直接拟合得出参数更具有实际物理意义。对比模型计算曲线与试验曲线发现,该模型可以较好地描述冻结砂土的衰减蠕变阶段和稳定蠕变阶段,为人工冻结法更好地应用于实际工程提供一种理论支撑。
